人教版九年级上 第24章 圆 单元测试(含答案)
文档属性
| 名称 | 人教版九年级上 第24章 圆 单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 194.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-25 07:53:54 | ||
图片预览



文档简介
人教版九年级上 第24章 圆 单元测试
一.选择题(共12小题)
1.如图,MN是⊙O的切线,M是切点,连结OM、ON.若∠N=38°,则∠MON度数为( )
A.38° B.42° C.52° D.62°
2.如图,OA是⊙O的半径,AB是⊙O的弦,OC⊥AB于点C,若OA=5,AB=8,则OC的长为( )
A.2 B.3 C.4 D.5
3.如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=50°,则∠C的度数为( )
A.60° B.50° C.40° D.30°
4.如图,⊙O中,弦AB,CD相交于点P,∠A=40°,∠B=45°,则∠APD=( )
A.40° B.45° C.15° D.85°
5.如图,AB为⊙O的直径,弦CD交AB于点E,CA=CE,若∠ACE=50°,则∠CBD的大小为( )
A.65° B.70° C.75° D.82.5°
6.如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,∠ACD=22.5°,AB=4,则CD的长为( )
A. B.2 C. D.
7.在⊙O中,点A,B,C,D在圆上,OB∥DC,OD∥BC,则∠A为( )
A.45° B.50° C.60° D.65°
8.如图⊙O1的半径O1A是⊙O2的直径,⊙O1的半径O1C交⊙O2于B,设弧AC的长是l1,弧AB的长是l2,那么( )
A.l1>l2 B.l1<l2
C.l1=l2 D.l1与l2的大小不能确定
9.如图,A,B,C,D是⊙O上的点,半径OA=3,=,∠DBC=25°,连接AD,则扇形AOB的面积为( )
A.π B.π C.π D.π
10.如图,CD是⊙O的直径,弦AB⊥CD,若∠CDB=28°,则∠AOC的度数为( )
A.28° B.56° C.58° D.62°
11.如图,PA,PB是⊙O的切线,切点分别为点A、B,点C为⊙O上一点,∠P=66°,则∠C等于( )
A.66° B.63° C.57° D.60°
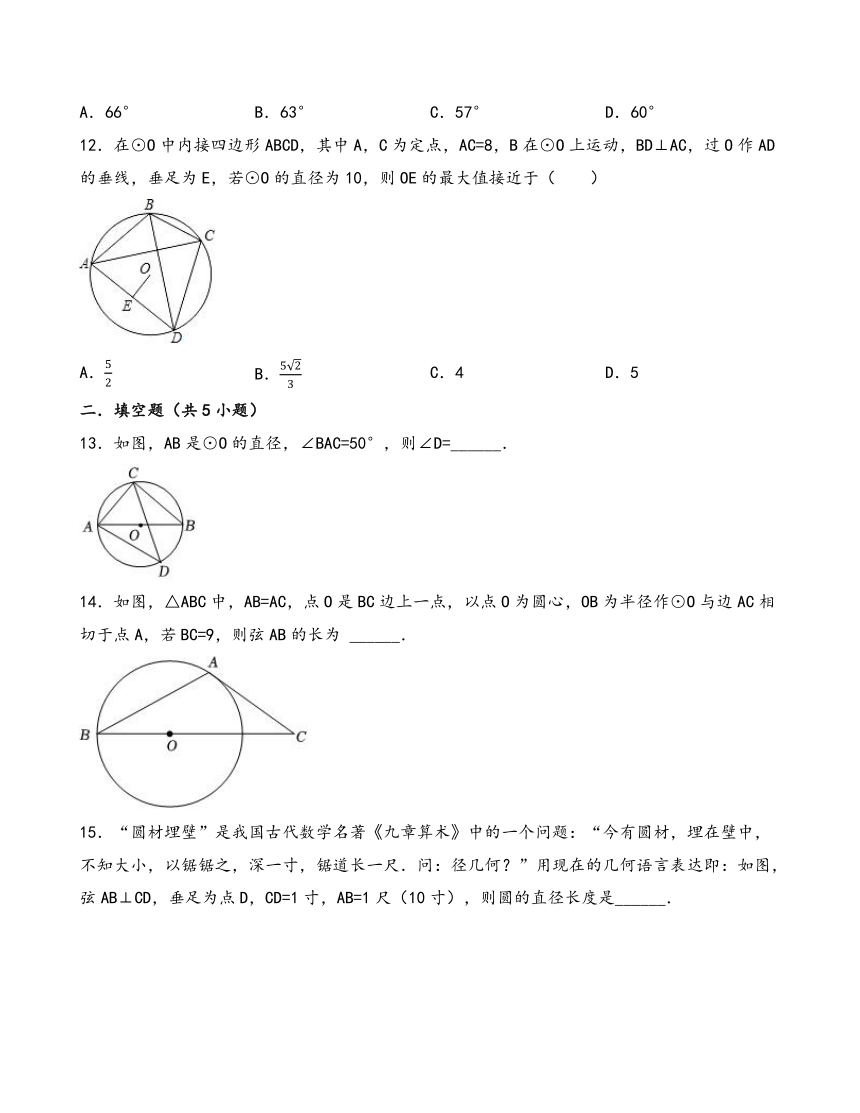
12.在⊙O中内接四边形ABCD,其中A,C为定点,AC=8,B在⊙O上运动,BD⊥AC,过O作AD的垂线,垂足为E,若⊙O的直径为10,则OE的最大值接近于( )
A. B. C.4 D.5
二.填空题(共5小题)
13.如图,AB是⊙O的直径,∠BAC=50°,则∠D=______.
14.如图,△ABC中,AB=AC,点O是BC边上一点,以点O为圆心,OB为半径作⊙O与边AC相切于点A,若BC=9,则弦AB的长为 ______.
15.“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何?”用现在的几何语言表达即:如图,弦AB⊥CD,垂足为点D,CD=1寸,AB=1尺(10寸),则圆的直径长度是______.
16.如图,AB是⊙O的直径,点C,D在⊙O上,连接CD,OD,AC,若∠BOD=124°,则∠ACD的度数等于 ______°.
17.如图,AB是⊙O的直径,BC是⊙O的切线,点B为切点.连接AC交⊙O于点D,点E是⊙O上一点,连接BE,DE过点A作AF∥BE交BD的延长线于点F.若BC=13,,∠F=∠ADE,则AB的长度是 ______,DF的长度是 ______.
三.解答题(共5小题)
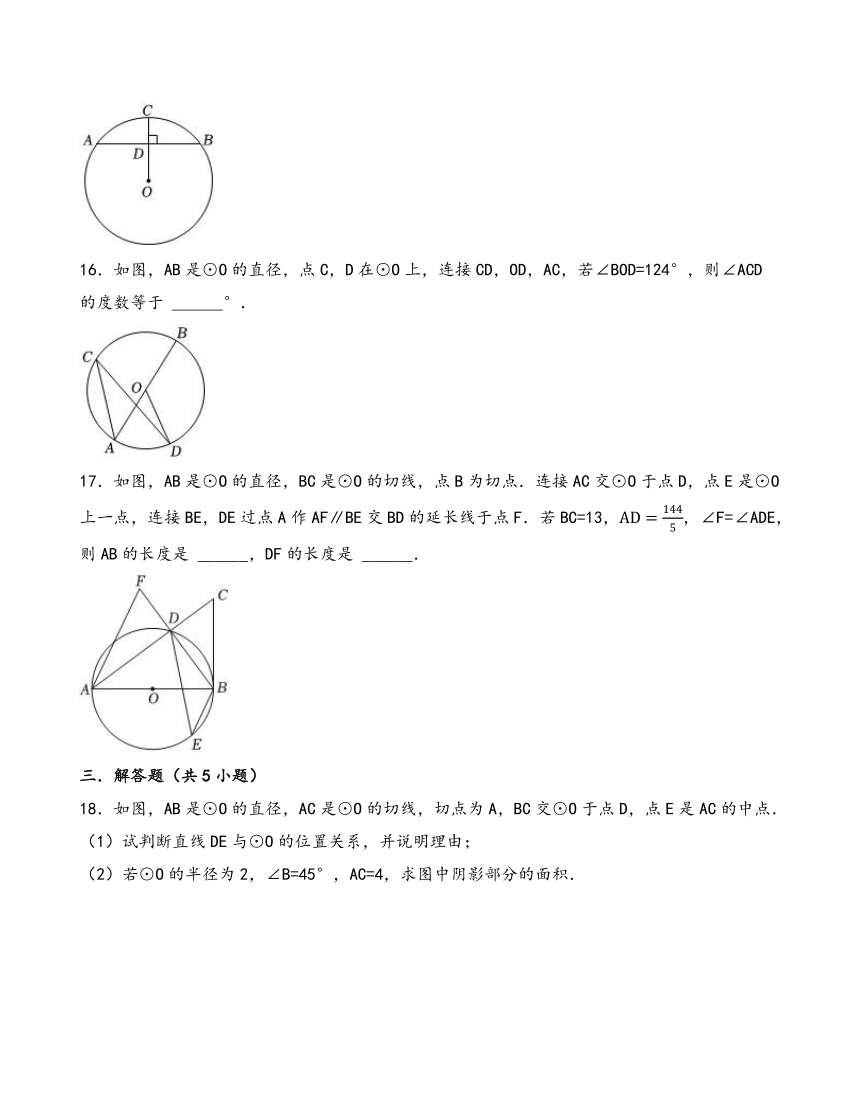
18.如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,∠B=45°,AC=4,求图中阴影部分的面积.
19.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,请直接写出弧AE的长.
20.如图,AB是⊙O的直径,过⊙O外一点P作⊙O的两条切线PC,PD,切点分别为C,D,连接OP,CD.
(1)求证:OP⊥CD;
(2)连接AD,BC,若∠DAB=50°,∠CBA=70°,OA=2,求OP的长.
21.日晷仪也称日晷,是观测日影计时的仪器.它是根据日影的位置,指定当时的时辰或刻数,是我国古代较为普遍使用的计时仪器.小东为了探究日晷的奥秘,在不同时刻对日晷进行了观察.如图,日晷的平面是以点O为圆心的圆,线段BC是日晷的底座,点D为日晷与底座的接触点(即BC与⊙O相切于点D).点A在⊙O上,OA为某一时刻晷针的影长,AO的延长线与⊙O交于点E,与BC交于点B,连接AC,OC,CE,BD=CD=3dm,OA⊥AC.
(1)求证:∠B=∠ACO;
(2)求CE的长.
22.如图,△ABC内接于圆O,AB是圆O的直径,点E在圆O上,点C是弧BE的中点,AE⊥CD,垂足为点D,DC的延长线交AB的延长线于点F.
(1)求证:CD是圆O的切线;
(2)若,∠ABC=60°,求线段AF的长.
人教版九年级上 第24章 圆 单元测试
(参考答案)
一.选择题(共12小题)
1、C 2、B 3、C 4、D 5、C 6、C 7、C 8、C 9、A 10、B 11、C 12、C
二.填空题(共5小题)
13、40°; 14、; 15、26寸; 16、28; 17、;;
三.解答题(共5小题)
18、解:(1)如图,连接AD,OD
∵AB是直径,
∴∠ADB=90°,
∴∠OAD=∠ODA,
∵点E是AC的中点,∠ADC=90°,
∴DE=AE,
∴∠ADE=∠EAD,
∵∠EAD+∠OAD=90°
∴∠ADE+∠ODA=90°,即∠EDO=90°,
∴直线DE与⊙O相切
(2)由(1)可知△ACD与△ADB是直角三角形
若∠B=45°,则AC=AB=4,AE=EC=AO=DO=BO=2
∴四边形AEDO为正方形
阴影面积=正方形AEDO-扇形AOD=4-π.
19、(1)证明:如图,连接OD,
∵OB=OD,
∴∠ABC=∠ODB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ODB=∠ACB,
∴OD∥AC,
∵过点D作⊙O的切线DF,交AC于点F,
∴DF⊥OD,
∴DF⊥AC.
(2)解:如图,连接OE,
∵DF⊥AC,∠CDF=22.5°,
∴∠ABC=∠ACB=67.5°,
∴∠BAC=45°,
∵OA=OE,
∴∠AOE=90°,
∵⊙O的半径为4,
∴弧AE的长为.
20、解:(1)方法1、连接OC,OD,
∴OC=OD,
∵PD,PC是⊙O的切线,
∵∠ODP=∠OCP=90°,
在Rt△ODP和Rt△OCP中,,
∴Rt△ODP≌Rt△OCP,
∴∠DOP=∠COP,
∵OD=OC,
∴OP⊥CD;
方法2、∵PD,PC是⊙O的切线,
∴PD=PC,
∵OD=OC,
∴P,O在CD的中垂线上,
∴OP⊥CD
(2)如图,连接OD,OC,
∴OA=OD=OC=OB=2,
∴∠ADO=∠DAO=50°,∠BCO=∠CBO=70°,
∴∠AOD=80°,∠BOC=40°,
∴∠COD=60°,
∵OD=OC,
∴△COD是等边三角形,
由(1)知,∠DOP=∠COP=30°,
在Rt△ODP中,OP==.
21、(1)证明:连接OD,
∵BC与⊙O相切于点D,
∴OD⊥BC,
∵BD=CD,
∴OB=OC,
∴∠OBC=∠OCB,
∵OD⊥BC,
∴∠ODC=∠OAC=90°,
在Rt△AOC与Rt△DOC中,
,
∴Rt△AOC≌Rt△DOC(HL),
∴∠ACO=∠DCO,
∴∠B=∠ACO;
(2)解:∵∠BAC=90°,
AC=CD=BD=3dm,
∴,
∴∠B=30°,
∵OB=OC,
∴∠B=∠OCB=30°,
∴∠AOC=60°,
∴OA=AC=(dm),
∴AE=2OA=2dm,
∴CE===(dm).
22、(1)证明:连接OC,则OA=OC,
∴∠OAC=∠OCA,
∵点C是的中点,
∴,
∴∠OAC=∠DAC,
∴∠OCA=∠DAC,
∴OC∥AD,
∵AE⊥CD,
∴CD⊥OC,
∴CD是⊙O的切线;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠ABC=60°,
∴∠BAC=90°-∠ABC=90°-60°=30°,
∴∠DAC=30°,
∵,
∴
∴,
∵∠F=90°-(∠BAC+∠DAC)=90°-(30°+30°)=30°,
∴AF=2AD=6.
一.选择题(共12小题)
1.如图,MN是⊙O的切线,M是切点,连结OM、ON.若∠N=38°,则∠MON度数为( )
A.38° B.42° C.52° D.62°
2.如图,OA是⊙O的半径,AB是⊙O的弦,OC⊥AB于点C,若OA=5,AB=8,则OC的长为( )
A.2 B.3 C.4 D.5
3.如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=50°,则∠C的度数为( )
A.60° B.50° C.40° D.30°
4.如图,⊙O中,弦AB,CD相交于点P,∠A=40°,∠B=45°,则∠APD=( )
A.40° B.45° C.15° D.85°
5.如图,AB为⊙O的直径,弦CD交AB于点E,CA=CE,若∠ACE=50°,则∠CBD的大小为( )
A.65° B.70° C.75° D.82.5°
6.如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为E,∠ACD=22.5°,AB=4,则CD的长为( )
A. B.2 C. D.
7.在⊙O中,点A,B,C,D在圆上,OB∥DC,OD∥BC,则∠A为( )
A.45° B.50° C.60° D.65°
8.如图⊙O1的半径O1A是⊙O2的直径,⊙O1的半径O1C交⊙O2于B,设弧AC的长是l1,弧AB的长是l2,那么( )
A.l1>l2 B.l1<l2
C.l1=l2 D.l1与l2的大小不能确定
9.如图,A,B,C,D是⊙O上的点,半径OA=3,=,∠DBC=25°,连接AD,则扇形AOB的面积为( )
A.π B.π C.π D.π
10.如图,CD是⊙O的直径,弦AB⊥CD,若∠CDB=28°,则∠AOC的度数为( )
A.28° B.56° C.58° D.62°
11.如图,PA,PB是⊙O的切线,切点分别为点A、B,点C为⊙O上一点,∠P=66°,则∠C等于( )
A.66° B.63° C.57° D.60°
12.在⊙O中内接四边形ABCD,其中A,C为定点,AC=8,B在⊙O上运动,BD⊥AC,过O作AD的垂线,垂足为E,若⊙O的直径为10,则OE的最大值接近于( )
A. B. C.4 D.5
二.填空题(共5小题)
13.如图,AB是⊙O的直径,∠BAC=50°,则∠D=______.
14.如图,△ABC中,AB=AC,点O是BC边上一点,以点O为圆心,OB为半径作⊙O与边AC相切于点A,若BC=9,则弦AB的长为 ______.
15.“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何?”用现在的几何语言表达即:如图,弦AB⊥CD,垂足为点D,CD=1寸,AB=1尺(10寸),则圆的直径长度是______.
16.如图,AB是⊙O的直径,点C,D在⊙O上,连接CD,OD,AC,若∠BOD=124°,则∠ACD的度数等于 ______°.
17.如图,AB是⊙O的直径,BC是⊙O的切线,点B为切点.连接AC交⊙O于点D,点E是⊙O上一点,连接BE,DE过点A作AF∥BE交BD的延长线于点F.若BC=13,,∠F=∠ADE,则AB的长度是 ______,DF的长度是 ______.
三.解答题(共5小题)
18.如图,AB是⊙O的直径,AC是⊙O的切线,切点为A,BC交⊙O于点D,点E是AC的中点.
(1)试判断直线DE与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为2,∠B=45°,AC=4,求图中阴影部分的面积.
19.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,请直接写出弧AE的长.
20.如图,AB是⊙O的直径,过⊙O外一点P作⊙O的两条切线PC,PD,切点分别为C,D,连接OP,CD.
(1)求证:OP⊥CD;
(2)连接AD,BC,若∠DAB=50°,∠CBA=70°,OA=2,求OP的长.
21.日晷仪也称日晷,是观测日影计时的仪器.它是根据日影的位置,指定当时的时辰或刻数,是我国古代较为普遍使用的计时仪器.小东为了探究日晷的奥秘,在不同时刻对日晷进行了观察.如图,日晷的平面是以点O为圆心的圆,线段BC是日晷的底座,点D为日晷与底座的接触点(即BC与⊙O相切于点D).点A在⊙O上,OA为某一时刻晷针的影长,AO的延长线与⊙O交于点E,与BC交于点B,连接AC,OC,CE,BD=CD=3dm,OA⊥AC.
(1)求证:∠B=∠ACO;
(2)求CE的长.
22.如图,△ABC内接于圆O,AB是圆O的直径,点E在圆O上,点C是弧BE的中点,AE⊥CD,垂足为点D,DC的延长线交AB的延长线于点F.
(1)求证:CD是圆O的切线;
(2)若,∠ABC=60°,求线段AF的长.
人教版九年级上 第24章 圆 单元测试
(参考答案)
一.选择题(共12小题)
1、C 2、B 3、C 4、D 5、C 6、C 7、C 8、C 9、A 10、B 11、C 12、C
二.填空题(共5小题)
13、40°; 14、; 15、26寸; 16、28; 17、;;
三.解答题(共5小题)
18、解:(1)如图,连接AD,OD
∵AB是直径,
∴∠ADB=90°,
∴∠OAD=∠ODA,
∵点E是AC的中点,∠ADC=90°,
∴DE=AE,
∴∠ADE=∠EAD,
∵∠EAD+∠OAD=90°
∴∠ADE+∠ODA=90°,即∠EDO=90°,
∴直线DE与⊙O相切
(2)由(1)可知△ACD与△ADB是直角三角形
若∠B=45°,则AC=AB=4,AE=EC=AO=DO=BO=2
∴四边形AEDO为正方形
阴影面积=正方形AEDO-扇形AOD=4-π.
19、(1)证明:如图,连接OD,
∵OB=OD,
∴∠ABC=∠ODB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ODB=∠ACB,
∴OD∥AC,
∵过点D作⊙O的切线DF,交AC于点F,
∴DF⊥OD,
∴DF⊥AC.
(2)解:如图,连接OE,
∵DF⊥AC,∠CDF=22.5°,
∴∠ABC=∠ACB=67.5°,
∴∠BAC=45°,
∵OA=OE,
∴∠AOE=90°,
∵⊙O的半径为4,
∴弧AE的长为.
20、解:(1)方法1、连接OC,OD,
∴OC=OD,
∵PD,PC是⊙O的切线,
∵∠ODP=∠OCP=90°,
在Rt△ODP和Rt△OCP中,,
∴Rt△ODP≌Rt△OCP,
∴∠DOP=∠COP,
∵OD=OC,
∴OP⊥CD;
方法2、∵PD,PC是⊙O的切线,
∴PD=PC,
∵OD=OC,
∴P,O在CD的中垂线上,
∴OP⊥CD
(2)如图,连接OD,OC,
∴OA=OD=OC=OB=2,
∴∠ADO=∠DAO=50°,∠BCO=∠CBO=70°,
∴∠AOD=80°,∠BOC=40°,
∴∠COD=60°,
∵OD=OC,
∴△COD是等边三角形,
由(1)知,∠DOP=∠COP=30°,
在Rt△ODP中,OP==.
21、(1)证明:连接OD,
∵BC与⊙O相切于点D,
∴OD⊥BC,
∵BD=CD,
∴OB=OC,
∴∠OBC=∠OCB,
∵OD⊥BC,
∴∠ODC=∠OAC=90°,
在Rt△AOC与Rt△DOC中,
,
∴Rt△AOC≌Rt△DOC(HL),
∴∠ACO=∠DCO,
∴∠B=∠ACO;
(2)解:∵∠BAC=90°,
AC=CD=BD=3dm,
∴,
∴∠B=30°,
∵OB=OC,
∴∠B=∠OCB=30°,
∴∠AOC=60°,
∴OA=AC=(dm),
∴AE=2OA=2dm,
∴CE===(dm).
22、(1)证明:连接OC,则OA=OC,
∴∠OAC=∠OCA,
∵点C是的中点,
∴,
∴∠OAC=∠DAC,
∴∠OCA=∠DAC,
∴OC∥AD,
∵AE⊥CD,
∴CD⊥OC,
∴CD是⊙O的切线;
(2)解:∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠ABC=60°,
∴∠BAC=90°-∠ABC=90°-60°=30°,
∴∠DAC=30°,
∵,
∴
∴,
∵∠F=90°-(∠BAC+∠DAC)=90°-(30°+30°)=30°,
∴AF=2AD=6.
同课章节目录
