2024-2025学年冀教版(2024)七年级数学下册期末真题专项练习 03 计算题(含答案)
文档属性
| 名称 | 2024-2025学年冀教版(2024)七年级数学下册期末真题专项练习 03 计算题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 90.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-25 04:57:09 | ||
图片预览




文档简介
2024-2025学年冀教版(2024)七年级数学下册期末真题
专项练习 03 计算题
一、计算题
1.(2024七下·石家庄期末)先化简,再求值:.其中,
2.(2024七下·石家庄期末)已知不等式组
(1)解该不等式组,并把解集在下面的数轴上表示出来;
(2)写出该不等式组的所有正整数解.
3.(2024七下·高阳期末)(1)解方程组:
(2)解不等式:
(3)解不等式组:,并写出所有整数解.
4.(2024七下·涿州期末)(1)计算:①
②
(2)解方程组成下等式组:
①解方程组:
②解不等式组,并写出满足不等式组的所有整数解.
5.(2024七下·宣化期末)解不等式组,并把它们的解集在数轴上表示出来.
6.(2024七下·宣化期末)解方程组
7.(2024七下·内丘期末)按要求完成下列各小题.
(1)计算:;
(2)因式分解:;
(3)利用简便方法计算:.
8.(2024七下·张北期末)解关于x,y的方程组时,珍珍发现方程组的解和方程组的解相同.
(1)求方程组的解;
(2)求关于t的不等式的最小整数解.
9.(2024七下·卢龙期末)因式分解:
(1);
(2).
10.(2024七下·万全期末)(1)解方程组;
(2)解不等式,并写出非正整数解.
11.(2024七下·兴隆期末)请按要求完成下列题目:
(1)解方程组:
(2)先化简,再求值:,其中.
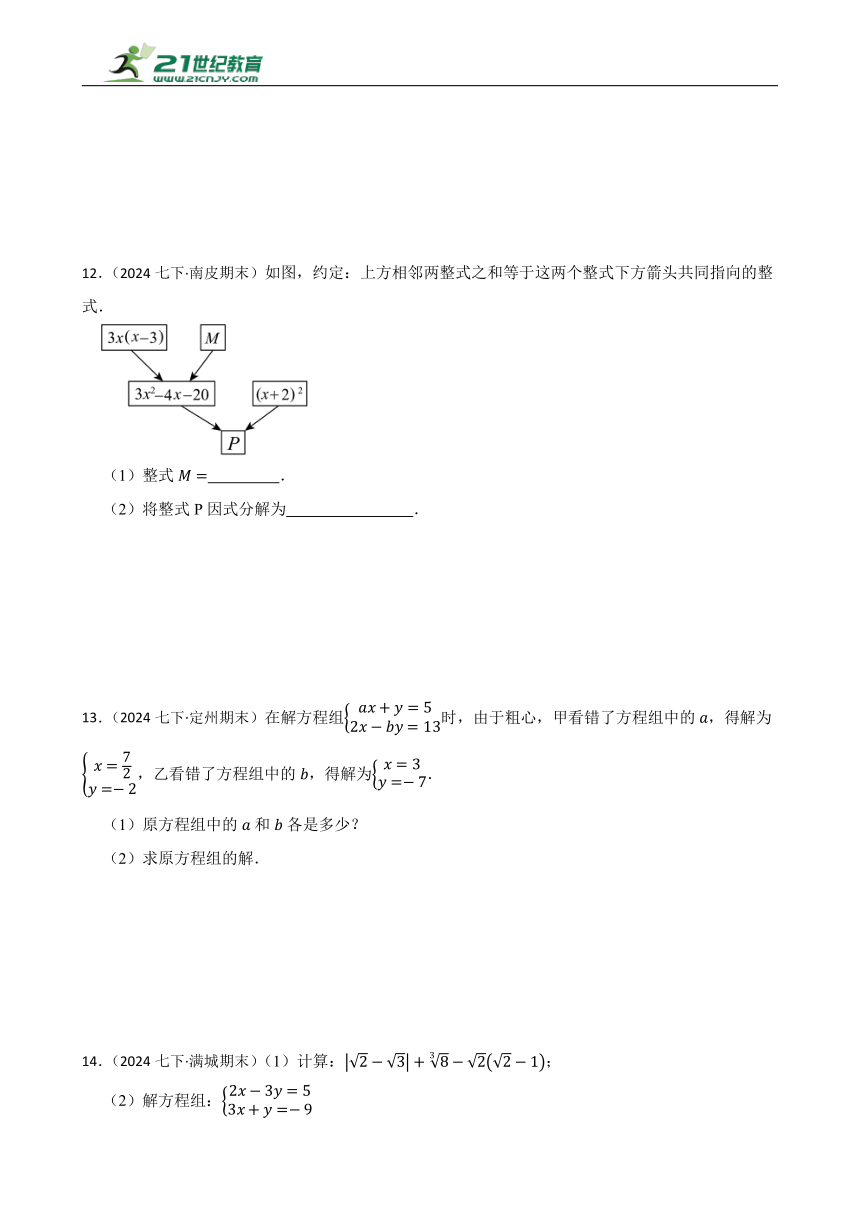
12.(2024七下·南皮期末)如图,约定:上方相邻两整式之和等于这两个整式下方箭头共同指向的整式.
(1)整式 .
(2)将整式P因式分解为 .
13.(2024七下·定州期末)在解方程组时,由于粗心,甲看错了方程组中的,得解为,乙看错了方程组中的,得解为.
(1)原方程组中的和各是多少?
(2)求原方程组的解.
14.(2024七下·满城期末)(1)计算:;
(2)解方程组:
15.(2024七下·长安期末)解答下列各题.
(1)因式分解:.
(2)计算:
16.(2024七下·正定期末)(1)解方程组:;
(2)计算:
(3)解不等式组:
17.(2024七下·栾城期末)(1)解方程组:
(2)解不等式组:
18.(2024七下·泊头期末)计算:
(1);
(2).
19.(2024七下·东光期末)解方程组.
20.(2024七下·莲池期末)计算
(1)
(2)
(3)
(4)(简便运算)
21.(2024七下·青龙期末)计算:
(1)解二元一次方程组:;
(2)解不等式组.
22.(2024七下·邯郸经济技术开发期末)因式分解:
(1)
(2)
23.(2024七下·惠阳期末)嘉淇准备完成题目:解不等式组时,发现常数“□”印刷不清楚.
(1)他把“□”猜成3,请你解不等式组;
(2)王老师说:我做一下变式,若不等式组的解集为,请求常数“□”的取值范围.
24.(2024七下·丛台期末)计算
(1)
(2)解方程组:
(3)解不等式组,并指出它的所有整数解.
25.(2024七下·朝阳期末)解方程组: .
26.(2024七下·邯山期末)已知方程组和有相同的解,求的值.
27.(2024七下·廊坊期末)解方程组:
(1)
(2)
28.(2024七下·乐业期末)先化简,再求值:,其中.
29.(2024七下·聊城期末)把下列各式因式分解.
(1);
(2).
答案解析部分
1.,
2.(1)解:
解不等式①,得,
解不等式②,得
原不等式组的解集为
不等式组的解集在数轴上表示如下:
(2)因为不等式组的解集为
所以不等式组的正整数解为:1,2.
(1)根据解一元一次不等式组的步骤对所给不等式组求解,并将解集在数轴上表示出来即可.
(2)根据(1)中求得的解集,写出此解集内的正整数解即可。
3.(1);(2);(3)不等式组的解集为,整数解为:
4.(1)①,②;
(2)①, ②,整数解有:,
5.解:
x-解得x,
1+3x2(2x-1)解得x3,
所以0.8x37分
把这个不等式组的解集表示在数轴上
由题意先求出每一个不等式的解集,再找出各解集的公共部分即为不等式组的解集;在数轴上表示解集时,再根据“<”空心向左、“≥”实心向右即可求解.
6.解:把①两边同时乘以3,得9x-6y=12③,
用②-③得9x-5y-9x+6y=13-12,解得y=1,
把y=1代入①得3x-2×1=4,解得x=2,
这个方程组的解为
观察方程组中未知数x的系数的最小公倍数是9,所以用方程②-①×3可消去未知数x,得到关于y的一元一次方程,解方程求得未知数y的值,把y的值代入①可求得x的值,再写出结论可求解.
7.(1)
(2)
(3)
8.(1)
(2)最小整数解为1
9.(1)
(2)
10.(1)
(2),非正整数解是
11.(1)
(2)
12.;
13.(1),;
(2)
14.(1);(2)
15.(1)解:
(2)解:原式
(1)首先提取公因式,得,再利用平方差公式分解因式即可得出结果原式=;
(2)根据多项式乘以多项式法则及单项式乘以多项式法则进行乘法运算,然后再合并同类项即可。
16.(1);(2);(3)
17.(1);(2)
18.(1)
(2)
19.
20.(1)
(2)
(3)
(4)
21.(1);
(2).
22.(1)
(2)
23.(1)
(2)
24.(1);(2);(3)-2<x≤2,整数解为-1,0,1,2
25.解:由第一个方程得 .代入第二个方程得 . 把 代入 得:∴这个方程组的解是
根据二元一次方程组的解法——代入消元法解之即可.
26.解:解方程组得,
把代入得,
解得,
则.
故答案为1.
先求出方程组的解为,再代入得出,求出的值,再代入进行计算即可.
27.(1)
(2)
28.a,9
29.(1)解:原式
;
(2)解:原式
.
(1)先提公因式x,再利用完全平方公式因式分解即可;
(2)先变形并提公因式,再利用平方差公式因式分解即可.
专项练习 03 计算题
一、计算题
1.(2024七下·石家庄期末)先化简,再求值:.其中,
2.(2024七下·石家庄期末)已知不等式组
(1)解该不等式组,并把解集在下面的数轴上表示出来;
(2)写出该不等式组的所有正整数解.
3.(2024七下·高阳期末)(1)解方程组:
(2)解不等式:
(3)解不等式组:,并写出所有整数解.
4.(2024七下·涿州期末)(1)计算:①
②
(2)解方程组成下等式组:
①解方程组:
②解不等式组,并写出满足不等式组的所有整数解.
5.(2024七下·宣化期末)解不等式组,并把它们的解集在数轴上表示出来.
6.(2024七下·宣化期末)解方程组
7.(2024七下·内丘期末)按要求完成下列各小题.
(1)计算:;
(2)因式分解:;
(3)利用简便方法计算:.
8.(2024七下·张北期末)解关于x,y的方程组时,珍珍发现方程组的解和方程组的解相同.
(1)求方程组的解;
(2)求关于t的不等式的最小整数解.
9.(2024七下·卢龙期末)因式分解:
(1);
(2).
10.(2024七下·万全期末)(1)解方程组;
(2)解不等式,并写出非正整数解.
11.(2024七下·兴隆期末)请按要求完成下列题目:
(1)解方程组:
(2)先化简,再求值:,其中.
12.(2024七下·南皮期末)如图,约定:上方相邻两整式之和等于这两个整式下方箭头共同指向的整式.
(1)整式 .
(2)将整式P因式分解为 .
13.(2024七下·定州期末)在解方程组时,由于粗心,甲看错了方程组中的,得解为,乙看错了方程组中的,得解为.
(1)原方程组中的和各是多少?
(2)求原方程组的解.
14.(2024七下·满城期末)(1)计算:;
(2)解方程组:
15.(2024七下·长安期末)解答下列各题.
(1)因式分解:.
(2)计算:
16.(2024七下·正定期末)(1)解方程组:;
(2)计算:
(3)解不等式组:
17.(2024七下·栾城期末)(1)解方程组:
(2)解不等式组:
18.(2024七下·泊头期末)计算:
(1);
(2).
19.(2024七下·东光期末)解方程组.
20.(2024七下·莲池期末)计算
(1)
(2)
(3)
(4)(简便运算)
21.(2024七下·青龙期末)计算:
(1)解二元一次方程组:;
(2)解不等式组.
22.(2024七下·邯郸经济技术开发期末)因式分解:
(1)
(2)
23.(2024七下·惠阳期末)嘉淇准备完成题目:解不等式组时,发现常数“□”印刷不清楚.
(1)他把“□”猜成3,请你解不等式组;
(2)王老师说:我做一下变式,若不等式组的解集为,请求常数“□”的取值范围.
24.(2024七下·丛台期末)计算
(1)
(2)解方程组:
(3)解不等式组,并指出它的所有整数解.
25.(2024七下·朝阳期末)解方程组: .
26.(2024七下·邯山期末)已知方程组和有相同的解,求的值.
27.(2024七下·廊坊期末)解方程组:
(1)
(2)
28.(2024七下·乐业期末)先化简,再求值:,其中.
29.(2024七下·聊城期末)把下列各式因式分解.
(1);
(2).
答案解析部分
1.,
2.(1)解:
解不等式①,得,
解不等式②,得
原不等式组的解集为
不等式组的解集在数轴上表示如下:
(2)因为不等式组的解集为
所以不等式组的正整数解为:1,2.
(1)根据解一元一次不等式组的步骤对所给不等式组求解,并将解集在数轴上表示出来即可.
(2)根据(1)中求得的解集,写出此解集内的正整数解即可。
3.(1);(2);(3)不等式组的解集为,整数解为:
4.(1)①,②;
(2)①, ②,整数解有:,
5.解:
x-解得x,
1+3x2(2x-1)解得x3,
所以0.8x37分
把这个不等式组的解集表示在数轴上
由题意先求出每一个不等式的解集,再找出各解集的公共部分即为不等式组的解集;在数轴上表示解集时,再根据“<”空心向左、“≥”实心向右即可求解.
6.解:把①两边同时乘以3,得9x-6y=12③,
用②-③得9x-5y-9x+6y=13-12,解得y=1,
把y=1代入①得3x-2×1=4,解得x=2,
这个方程组的解为
观察方程组中未知数x的系数的最小公倍数是9,所以用方程②-①×3可消去未知数x,得到关于y的一元一次方程,解方程求得未知数y的值,把y的值代入①可求得x的值,再写出结论可求解.
7.(1)
(2)
(3)
8.(1)
(2)最小整数解为1
9.(1)
(2)
10.(1)
(2),非正整数解是
11.(1)
(2)
12.;
13.(1),;
(2)
14.(1);(2)
15.(1)解:
(2)解:原式
(1)首先提取公因式,得,再利用平方差公式分解因式即可得出结果原式=;
(2)根据多项式乘以多项式法则及单项式乘以多项式法则进行乘法运算,然后再合并同类项即可。
16.(1);(2);(3)
17.(1);(2)
18.(1)
(2)
19.
20.(1)
(2)
(3)
(4)
21.(1);
(2).
22.(1)
(2)
23.(1)
(2)
24.(1);(2);(3)-2<x≤2,整数解为-1,0,1,2
25.解:由第一个方程得 .代入第二个方程得 . 把 代入 得:∴这个方程组的解是
根据二元一次方程组的解法——代入消元法解之即可.
26.解:解方程组得,
把代入得,
解得,
则.
故答案为1.
先求出方程组的解为,再代入得出,求出的值,再代入进行计算即可.
27.(1)
(2)
28.a,9
29.(1)解:原式
;
(2)解:原式
.
(1)先提公因式x,再利用完全平方公式因式分解即可;
(2)先变形并提公因式,再利用平方差公式因式分解即可.
同课章节目录
