2024-2025学年冀教版(2024)七年级数学下册期末真题专项练习 04 解答题(含答案)
文档属性
| 名称 | 2024-2025学年冀教版(2024)七年级数学下册期末真题专项练习 04 解答题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 472.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-25 04:56:26 | ||
图片预览



文档简介
2024-2025学年冀教版(2024)七年级数学下册期末真题
专项练习 04 解答题
一、解答题
1.(2024七下·石家庄期末)学习了《整式的乘除》这一章之后,小明联想到小学除法运算时,会碰到余数的问题,那么多项式除法类比着也会出现余式的问题.例如,如果一个多项式(设该多项式为A)除以的商为,余式为,那么这个多项式是多少?
他通过类比小学除法的运算法则:
被除数=除数×商+余数,推理出多项式除法法则:被除式=除式×商+余式.请根据以上材料,解决下列问题:
(1)请你帮小明求出多项式A;
(2)小明继续探索,已知关于x的多项式除以的商为,余式为x,请你根据以上法则,求出m,n的值.
2.(2024七下·满城期末)新定义:若某一元一次方程的解在某一元一次不等式组解集范围内,则称该一元一次方程为该不等式组的“关联方程”,例如:方程的解为,而不等式组 的解集为,不难发现在的范围内,所以方程是不等式组 的“关联方程”.
(1)在方程①;②;③中,关于的不等式组 的“关联方程”是 ;(填序号)
(2)若关于的方程是不等式组的“关联方程”,求的取值范围;
3.(2024七下·青县期末)在平面直角坐标系中,三角形经过平移得到三角形,位置如图所示.
(1)分别写出点,的坐标;
(2)请说明三角形是由三角形经过怎样的平移得到的;
(3)若点是三角形内部一点,则平移后对应点的坐标为,求m和n的值.
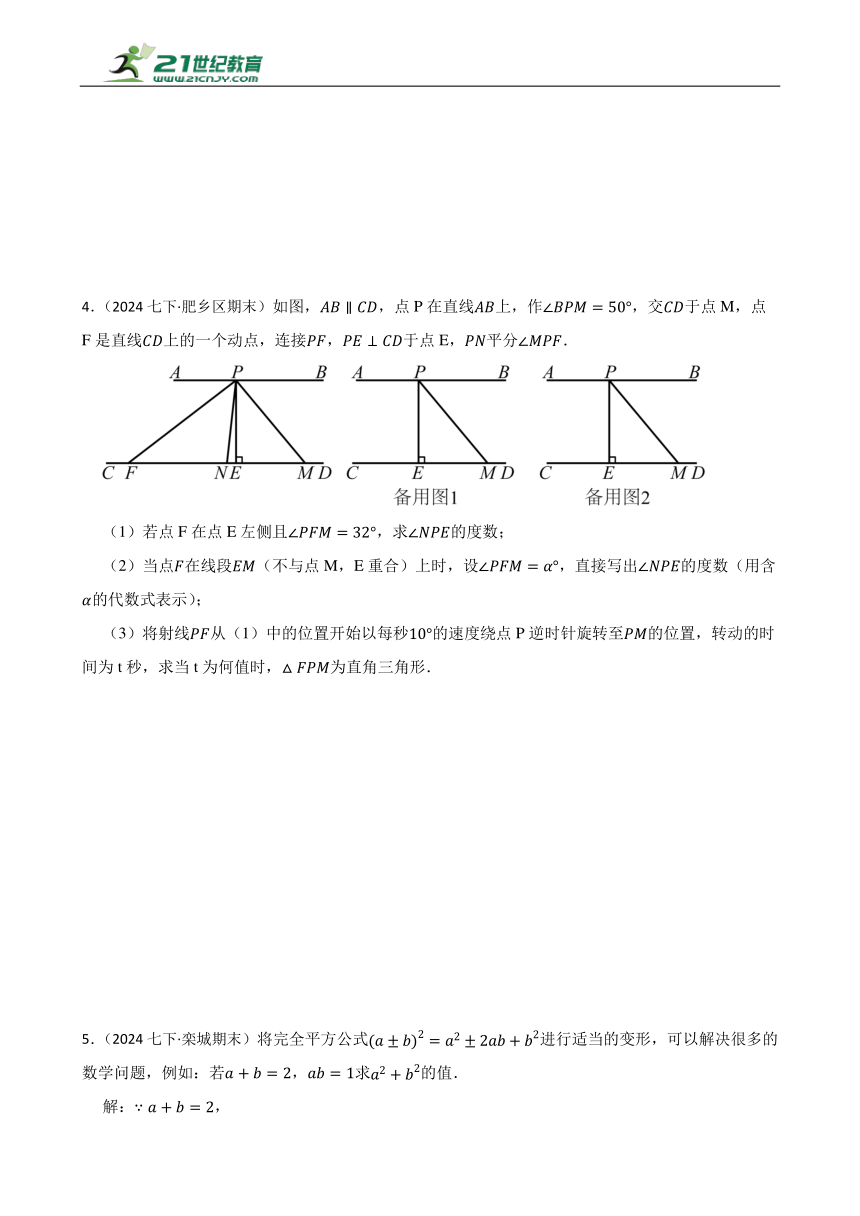
4.(2024七下·肥乡区期末)如图,,点P在直线上,作,交于点M,点F是直线上的一个动点,连接,于点E,平分.
(1)若点F在点E左侧且,求的度数;
(2)当点在线段(不与点M,E重合)上时,设,直接写出的度数(用含的代数式表示);
(3)将射线从(1)中的位置开始以每秒的速度绕点P逆时针旋转至的位置,转动的时间为t秒,求当t为何值时,为直角三角形.
5.(2024七下·栾城期末)将完全平方公式进行适当的变形,可以解决很多的数学问题,例如:若,求的值.
解:,
,即.
又,
,得.
根据上面的解题思路与方法,解决下列问题:
(1)若,,则__________;
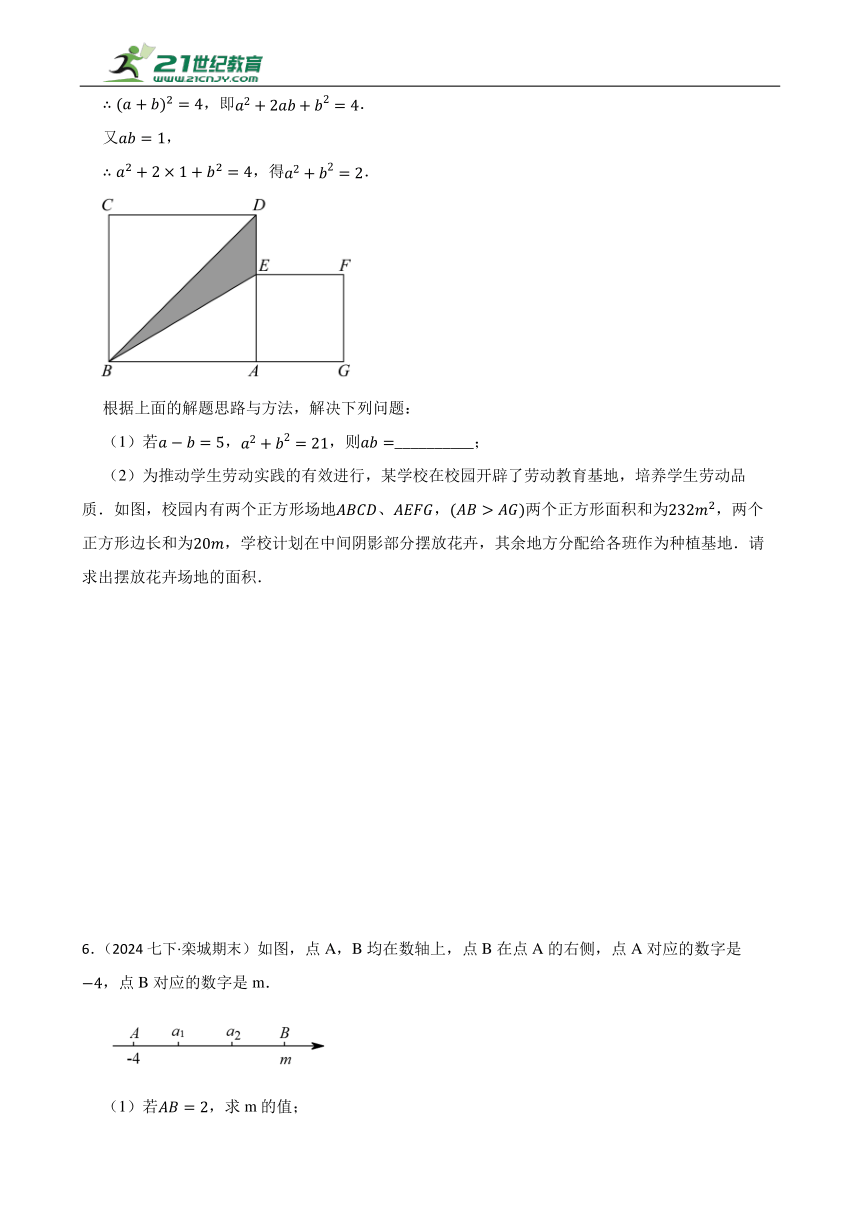
(2)为推动学生劳动实践的有效进行,某学校在校园开辟了劳动教育基地,培养学生劳动品质.如图,校园内有两个正方形场地、,两个正方形面积和为,两个正方形边长和为,学校计划在中间阴影部分摆放花卉,其余地方分配给各班作为种植基地.请求出摆放花卉场地的面积.
6.(2024七下·栾城期末)如图,点A,B均在数轴上,点B在点A的右侧,点A对应的数字是,点B对应的数字是m.
(1)若,求m的值;
(2)将线段三等分,这两个等分点所对应数字从左到右依次是,,若,求m的取值范围.
7.(2024七下·泊头期末)对于任意实数,约定关于的一种运算如下:.例如:.
(1)若满足,求的取值范围;
(2)若,且,求的值.
8.(2024七下·东光期末)2022年北京冬奥会、冬残奥会已圆满结束,活泼敦厚的“冰墩墩”,喜庆祥和的“雪容融”引起广大民众的喜爱.王老师想要购买这两种吉祥物作为本次冬奥会的纪念品,已知购买2件“冰墩墩”和1件“雪容融”共需150元,购买3件“冰墩墩”和2件“雪容融”共需245元.
(1)求“冰墩墩”和“雪容融”的单价;
(2)学校现需一次性购买上述型号的“冰墩墩”和“雪容融”纪念品共100个,要求购买的总费用不超过5000元,则最多可以购买多少个“冰墩墩”?
9.(2024七下·东光期末)对于平面直角坐标系中的点,若点的坐标为其中为常数,且,则称点为点的“n属派生点”.
例如:的“2属派生点”为,即.
(1)点的“属派生点”的坐标为______ ;
(2)若点的“属派生点”的坐标为,则的值为______ ;
(3)若点在轴上,点的“属派生点”为点,且线段的长度为线段长度的倍,求的值.
10.(2024七下·海兴期末)在平面直角坐标系中,对于点P,给出如下定义:点P的“甲变换”:将点P向左平移1个单位长度,再向上平移2个单位长度;点P的“乙变换”:将点 P向右平移2个单位长度,再向下平移1个单位长度.
(1)若对点进行1次“甲变换”后得到点的坐标为 ,若对点 B进行1次“乙变换”后得到点,则点 B 的坐标为 ;
(2)若对点进行1次“甲变换”, 再进行2次“乙变换”后, 所得到的点D落在y轴上,求m的值及点 D的坐标;
(3)若对点进行“甲变换”和“乙变换”共计10次后得到点 Q, 恰好落在x轴上,直接写出点 Q 的坐标.
11.(2024七下·清苑期末)从简单情况入手,观察猜想,发现规律,运用规律解决问题,这是常见的研究数学问题的思路.
问题解决:
(1)填空:
________
________
猜想:
________
总结结论:
(2)填空:当n为正整数时,________.利用这个结论,请你解决下面的问题:求的值.
12.(2024七下·石家庄期末)在学习用乘法公式分解因式时,我们知道把多项式及叫做“完全平方式”.杨老师布置了一道思维拓展题:代数式有最大值还是最小值?并求出这个最值.小宋的解题步骤如下:
的最小值为4
小宋的解法及结果得到了杨老师的肯定,请根据上述内容完成以下问题:
(1)下列多项式中①;③;③④是完全平方式的有______.(请填写序号)
(2)若是一个完全平方式,则的值等于______为常数).
(3)代数式有最大值还是最小值?并求出这个最值.
13.(2024七下·随县期末)为拓展学生视野,某中学组织八年级师生开展研学活动,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出三辆车,且其余客车恰好坐满.现有甲、乙两种客车,它们的载客量和租金如下表所示:
甲型客车 乙型客车
载客量(人/辆) 45 60
租金(元/辆) 200 300
(1)参加此次研学活动的师生人数是多少?原计划租用多少辆45座客车?
(2)若租用同一种客车,要使每位师生都有座位,应该怎样租用才合算?
14.(2024七下·莲池期末)若满足 ,求 的值.阅读下面求解的方法:
解:设(,则
∴.
请仿照上面的方法求解下面的问题:
(1)若满足 求 的值;
(2)如图,正方形中,E、F 分别是、上的点,且,长方形的面积是15,分别以、为边作正方形,若,则
① (用含x的代数式表示);
②直接写出图中阴影部分的面积.
15.(2024七下·广平期末)如图所示,在中,是角平分线.
(1),,求的度数,并说明理由.
(2)题(1)中,如将“,”改为“”,求的度数.
(3)若,直接写出的度数.
16.(2024七下·广平期末)整式的值为P.
(1)当时,求P的值;
(2)若P的取值范围如图所示,求m的最小负整数值.
17.(2024七下·任丘期末)对于任意实数、,定义关于“”的一种运算如下:.例如.
(1)求的值;
(2)若,且,求的值.
18.(2024七下·丛台期末)如图①,在△ABC 中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=70°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q,∠A之间的数量关系.
(3)如图③,延长线段BP,QC交于点E,在△BQE中,存在一个内角等于另一个内角的3倍,求∠A的度数.
19.(2024七下·丛台期末)某学校为提高办学条件,计划在每一个教室安装一台Ⅰ型电脑或者Ⅱ型电脑.经市场调查发现,若购买台Ⅰ型电脑和台Ⅱ型电脑共需元;购买台Ⅰ型电脑比购买台Ⅱ型电脑多元.
(1)求每台Ⅰ型电脑和Ⅱ型电脑的价格;
(2)现有两家商场分别推出了优惠套餐:
甲商场:Ⅰ型电脑和Ⅱ型电脑均打八折出售.
乙商场:Ⅰ型电脑每满元减元,Ⅱ型电脑无优惠活动.
该校需要购买Ⅰ型电脑和Ⅱ型电脑共台,且只能选择一家商场购买,则该学校至少购买多少台Ⅰ型电脑才能使选择乙商场购买更划算?
20.(2024七下·新华期末)如图,在三角形中,,,.将三角形沿向左平移,得到三角形,与交于点,连接.
(1)分别求和的度数;
(2)若,,求图中阴影部分的面积;
(3)已知点在三角形约内部,三角形平移到三角形后,点的对应点为,连接.若三角形的周长为,四边形的周长为,请直接写出的长度.
21.如图是一种躺椅及其结构示意图,扶手AB与底座CD都平行于地面EF,前支架OE与后支架OF分别与CD交于点G和点D,AB与DM交于点N,∠AOE=∠BNM.
(1)请对说明理由;
(2)若OE平分∠AOF,∠ODC=30°,求扶手AB与靠背DM的夹角∠ANM的度数.
22.(2024七下·邯山期末)按要求解答下列各题
(1)解不等式,并把解集在数轴上表示出来;
(2)解不等式组,把解集在数轴上表示出来.
23.(2020七下·阜平期末)长沙市某公园的门票价格如下表所示:
购票人数 1~50人 51~100人 100人以上
票价 10元/人 8元/人 5元/人
某校九年级甲、乙两个班共100多人去该公园举行毕业联欢活动,其中甲班有50多人,乙班不足50人,如果以班为单位分别买门票,两个班一共应付920元;如果两个班联合起来作为一个团体购票,一共要付515元,问甲、乙两班分别有多少人
24.(2022七下·南宫期末)如图,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
25.(2020七下·肇州期末)如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC,请判断CD与AB的位置关系,并说明理由.
26.(2024七下·西岗期末)如果一元一次方程的解也是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.例如:方程的解为,不等式组的解集为,因为,所以称方程为不等式组的关联方程.
(1)在方程①;②;③中,不等式组的关联方程是___________.(填序号)
(2)若不等式组的一个关联方程的解是整数,则这个关联方程可以是___________.(写出一个即可)
(3)若方程都是关于的不等式组的关联方程,求的取值范围.
答案解析部分
1.(1)
(2)
2.(1)①②
(2)
3.(1),
(2)左移5个单位长度,上移4个单位长度
(3)
4.(1)9°
(2)
(3)为秒或秒
5.(1)
(2)
6.(1)
(2)
7.(1);
(2).
8.(1)“冰墩墩”的单价为55元,“雪容融”的单价为40元
(2)最多可以购买66个“冰墩墩”
9.(1)
(2)2
(3)
10.(1),
(2);
(3)
11.(1);;;(2);
12.(1)②④
(2)
(3)代数式有最大值,最大值为.
13.(1)参加此次研学活动的师生有600人,原计划租用45座客车13辆
(2)租14辆45座客车较合算
14.(1)10
(2)① ,;②图中阴影部分的面积为16
15.(1)
(2)
(3)
16.(1)
(2)的最小负整数值为
17.(1);(2).
18.(1)
(2)
(3)∠A的度数是或或或
19.(1)元,元;
(2)台.
20.(1);
(2)10
(3)6
21.(1)解:理由如下:∵∠BNM=∠AND,∠AOE=∠BNM,∴∠AOE=∠AND,
∴OE∥DM;
(2)解:∵AB与底座CD都平行于地面EF,∴AB∥CD,∴∠BOD=∠ODC=30°,
∵∠AOF+∠BOD=180°,∴∠AOF=150°,
∵OE平分∠AOF,∴∠EOF=∠AOF=75°,∴∠BOE=∠BOD+∠EOF=105°,
∵OE∥DM,∴∠ANM=∠BOE=105°.
(1)先利用对顶角相等,得到 ∠BNM=∠AND ,再根据同位角相等,即 ∠AOE=∠AND ,证明两直线平行;
(2)根据平角性质,得到 ∠AOF+∠BOD=180° ,再结合题目条件,求出∠AOF=150°,又已知OE平分∠AOF , ∠ODC=30°, 算出 ∠EOF=75° ,继而可算出 ∠BOE=∠BOD+∠EOF=105° ,在利用 OE∥DM ,内错角相等,最后推出 ∠ANM=∠BOE=105° 。
22.(1)解:解:,
,
在数轴上表示如下:
故答案为:,
在数轴上表示如下:
.
(2)解:解:,解不等式①可得:,
∴
解不等式②可得:
∴,
∴不等式组的解集为;
在数轴上表示如下:
故答案为:不等式组的解集为,
在数轴上表示如下:
(1)根据解不等式的一般步骤:先移项,合并同类项,化系数为1 求出不等式的解集,然后在数轴上表示出来即可;
(2)不等式①先去括号,再解不等式,不等式②先去分母,去括号再解不等式,分别求出两个不等式的解集,根据口诀:大大取大,小小取小,大小小大中间找,大大小小找不到,再确定不等式组的解集,最后在数轴上表示出来即可.
23.解:设甲、乙两班分别有x、y人.
根据题意得
解得
故甲班有55人,乙班有48人.
设甲、乙两班分别有x、y人,根据题意列出二元一次方程组求解即可。
24.解:∵EF∥BC,
∴∠BAF=180°﹣∠B=100°,
∵AC平分∠BAF,
∴∠CAF= ∠BAF=50°,
∵EF∥BC,
∴∠C=∠CAF=50°
根据两直线平行,同旁内角互补求出∠BAF,再根据角平分线的定义求出∠CAF,然后根据两直线平行,内错角相等解答.
25.解:CD⊥AB.理由如下:
∴DG∥BC,
∴∠1=∠DCB,
∵∠1=∠2,
∴∠2=∠DCB,
∴CD∥EF,
∴∠CDB=∠EFB,
∵EF⊥AB,
∴∠EFB=90°,
∴∠CDB=90°,
∴CD⊥AB.
由平行线的性质和已知条件可证明CD∥EF,可求得∠CDB=90°,可判断CD⊥AB.
26.(1)①;(2);(3)
专项练习 04 解答题
一、解答题
1.(2024七下·石家庄期末)学习了《整式的乘除》这一章之后,小明联想到小学除法运算时,会碰到余数的问题,那么多项式除法类比着也会出现余式的问题.例如,如果一个多项式(设该多项式为A)除以的商为,余式为,那么这个多项式是多少?
他通过类比小学除法的运算法则:
被除数=除数×商+余数,推理出多项式除法法则:被除式=除式×商+余式.请根据以上材料,解决下列问题:
(1)请你帮小明求出多项式A;
(2)小明继续探索,已知关于x的多项式除以的商为,余式为x,请你根据以上法则,求出m,n的值.
2.(2024七下·满城期末)新定义:若某一元一次方程的解在某一元一次不等式组解集范围内,则称该一元一次方程为该不等式组的“关联方程”,例如:方程的解为,而不等式组 的解集为,不难发现在的范围内,所以方程是不等式组 的“关联方程”.
(1)在方程①;②;③中,关于的不等式组 的“关联方程”是 ;(填序号)
(2)若关于的方程是不等式组的“关联方程”,求的取值范围;
3.(2024七下·青县期末)在平面直角坐标系中,三角形经过平移得到三角形,位置如图所示.
(1)分别写出点,的坐标;
(2)请说明三角形是由三角形经过怎样的平移得到的;
(3)若点是三角形内部一点,则平移后对应点的坐标为,求m和n的值.
4.(2024七下·肥乡区期末)如图,,点P在直线上,作,交于点M,点F是直线上的一个动点,连接,于点E,平分.
(1)若点F在点E左侧且,求的度数;
(2)当点在线段(不与点M,E重合)上时,设,直接写出的度数(用含的代数式表示);
(3)将射线从(1)中的位置开始以每秒的速度绕点P逆时针旋转至的位置,转动的时间为t秒,求当t为何值时,为直角三角形.
5.(2024七下·栾城期末)将完全平方公式进行适当的变形,可以解决很多的数学问题,例如:若,求的值.
解:,
,即.
又,
,得.
根据上面的解题思路与方法,解决下列问题:
(1)若,,则__________;
(2)为推动学生劳动实践的有效进行,某学校在校园开辟了劳动教育基地,培养学生劳动品质.如图,校园内有两个正方形场地、,两个正方形面积和为,两个正方形边长和为,学校计划在中间阴影部分摆放花卉,其余地方分配给各班作为种植基地.请求出摆放花卉场地的面积.
6.(2024七下·栾城期末)如图,点A,B均在数轴上,点B在点A的右侧,点A对应的数字是,点B对应的数字是m.
(1)若,求m的值;
(2)将线段三等分,这两个等分点所对应数字从左到右依次是,,若,求m的取值范围.
7.(2024七下·泊头期末)对于任意实数,约定关于的一种运算如下:.例如:.
(1)若满足,求的取值范围;
(2)若,且,求的值.
8.(2024七下·东光期末)2022年北京冬奥会、冬残奥会已圆满结束,活泼敦厚的“冰墩墩”,喜庆祥和的“雪容融”引起广大民众的喜爱.王老师想要购买这两种吉祥物作为本次冬奥会的纪念品,已知购买2件“冰墩墩”和1件“雪容融”共需150元,购买3件“冰墩墩”和2件“雪容融”共需245元.
(1)求“冰墩墩”和“雪容融”的单价;
(2)学校现需一次性购买上述型号的“冰墩墩”和“雪容融”纪念品共100个,要求购买的总费用不超过5000元,则最多可以购买多少个“冰墩墩”?
9.(2024七下·东光期末)对于平面直角坐标系中的点,若点的坐标为其中为常数,且,则称点为点的“n属派生点”.
例如:的“2属派生点”为,即.
(1)点的“属派生点”的坐标为______ ;
(2)若点的“属派生点”的坐标为,则的值为______ ;
(3)若点在轴上,点的“属派生点”为点,且线段的长度为线段长度的倍,求的值.
10.(2024七下·海兴期末)在平面直角坐标系中,对于点P,给出如下定义:点P的“甲变换”:将点P向左平移1个单位长度,再向上平移2个单位长度;点P的“乙变换”:将点 P向右平移2个单位长度,再向下平移1个单位长度.
(1)若对点进行1次“甲变换”后得到点的坐标为 ,若对点 B进行1次“乙变换”后得到点,则点 B 的坐标为 ;
(2)若对点进行1次“甲变换”, 再进行2次“乙变换”后, 所得到的点D落在y轴上,求m的值及点 D的坐标;
(3)若对点进行“甲变换”和“乙变换”共计10次后得到点 Q, 恰好落在x轴上,直接写出点 Q 的坐标.
11.(2024七下·清苑期末)从简单情况入手,观察猜想,发现规律,运用规律解决问题,这是常见的研究数学问题的思路.
问题解决:
(1)填空:
________
________
猜想:
________
总结结论:
(2)填空:当n为正整数时,________.利用这个结论,请你解决下面的问题:求的值.
12.(2024七下·石家庄期末)在学习用乘法公式分解因式时,我们知道把多项式及叫做“完全平方式”.杨老师布置了一道思维拓展题:代数式有最大值还是最小值?并求出这个最值.小宋的解题步骤如下:
的最小值为4
小宋的解法及结果得到了杨老师的肯定,请根据上述内容完成以下问题:
(1)下列多项式中①;③;③④是完全平方式的有______.(请填写序号)
(2)若是一个完全平方式,则的值等于______为常数).
(3)代数式有最大值还是最小值?并求出这个最值.
13.(2024七下·随县期末)为拓展学生视野,某中学组织八年级师生开展研学活动,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出三辆车,且其余客车恰好坐满.现有甲、乙两种客车,它们的载客量和租金如下表所示:
甲型客车 乙型客车
载客量(人/辆) 45 60
租金(元/辆) 200 300
(1)参加此次研学活动的师生人数是多少?原计划租用多少辆45座客车?
(2)若租用同一种客车,要使每位师生都有座位,应该怎样租用才合算?
14.(2024七下·莲池期末)若满足 ,求 的值.阅读下面求解的方法:
解:设(,则
∴.
请仿照上面的方法求解下面的问题:
(1)若满足 求 的值;
(2)如图,正方形中,E、F 分别是、上的点,且,长方形的面积是15,分别以、为边作正方形,若,则
① (用含x的代数式表示);
②直接写出图中阴影部分的面积.
15.(2024七下·广平期末)如图所示,在中,是角平分线.
(1),,求的度数,并说明理由.
(2)题(1)中,如将“,”改为“”,求的度数.
(3)若,直接写出的度数.
16.(2024七下·广平期末)整式的值为P.
(1)当时,求P的值;
(2)若P的取值范围如图所示,求m的最小负整数值.
17.(2024七下·任丘期末)对于任意实数、,定义关于“”的一种运算如下:.例如.
(1)求的值;
(2)若,且,求的值.
18.(2024七下·丛台期末)如图①,在△ABC 中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=70°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q,∠A之间的数量关系.
(3)如图③,延长线段BP,QC交于点E,在△BQE中,存在一个内角等于另一个内角的3倍,求∠A的度数.
19.(2024七下·丛台期末)某学校为提高办学条件,计划在每一个教室安装一台Ⅰ型电脑或者Ⅱ型电脑.经市场调查发现,若购买台Ⅰ型电脑和台Ⅱ型电脑共需元;购买台Ⅰ型电脑比购买台Ⅱ型电脑多元.
(1)求每台Ⅰ型电脑和Ⅱ型电脑的价格;
(2)现有两家商场分别推出了优惠套餐:
甲商场:Ⅰ型电脑和Ⅱ型电脑均打八折出售.
乙商场:Ⅰ型电脑每满元减元,Ⅱ型电脑无优惠活动.
该校需要购买Ⅰ型电脑和Ⅱ型电脑共台,且只能选择一家商场购买,则该学校至少购买多少台Ⅰ型电脑才能使选择乙商场购买更划算?
20.(2024七下·新华期末)如图,在三角形中,,,.将三角形沿向左平移,得到三角形,与交于点,连接.
(1)分别求和的度数;
(2)若,,求图中阴影部分的面积;
(3)已知点在三角形约内部,三角形平移到三角形后,点的对应点为,连接.若三角形的周长为,四边形的周长为,请直接写出的长度.
21.如图是一种躺椅及其结构示意图,扶手AB与底座CD都平行于地面EF,前支架OE与后支架OF分别与CD交于点G和点D,AB与DM交于点N,∠AOE=∠BNM.
(1)请对说明理由;
(2)若OE平分∠AOF,∠ODC=30°,求扶手AB与靠背DM的夹角∠ANM的度数.
22.(2024七下·邯山期末)按要求解答下列各题
(1)解不等式,并把解集在数轴上表示出来;
(2)解不等式组,把解集在数轴上表示出来.
23.(2020七下·阜平期末)长沙市某公园的门票价格如下表所示:
购票人数 1~50人 51~100人 100人以上
票价 10元/人 8元/人 5元/人
某校九年级甲、乙两个班共100多人去该公园举行毕业联欢活动,其中甲班有50多人,乙班不足50人,如果以班为单位分别买门票,两个班一共应付920元;如果两个班联合起来作为一个团体购票,一共要付515元,问甲、乙两班分别有多少人
24.(2022七下·南宫期末)如图,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
25.(2020七下·肇州期末)如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上,且EF⊥AB,DG∥BC,请判断CD与AB的位置关系,并说明理由.
26.(2024七下·西岗期末)如果一元一次方程的解也是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.例如:方程的解为,不等式组的解集为,因为,所以称方程为不等式组的关联方程.
(1)在方程①;②;③中,不等式组的关联方程是___________.(填序号)
(2)若不等式组的一个关联方程的解是整数,则这个关联方程可以是___________.(写出一个即可)
(3)若方程都是关于的不等式组的关联方程,求的取值范围.
答案解析部分
1.(1)
(2)
2.(1)①②
(2)
3.(1),
(2)左移5个单位长度,上移4个单位长度
(3)
4.(1)9°
(2)
(3)为秒或秒
5.(1)
(2)
6.(1)
(2)
7.(1);
(2).
8.(1)“冰墩墩”的单价为55元,“雪容融”的单价为40元
(2)最多可以购买66个“冰墩墩”
9.(1)
(2)2
(3)
10.(1),
(2);
(3)
11.(1);;;(2);
12.(1)②④
(2)
(3)代数式有最大值,最大值为.
13.(1)参加此次研学活动的师生有600人,原计划租用45座客车13辆
(2)租14辆45座客车较合算
14.(1)10
(2)① ,;②图中阴影部分的面积为16
15.(1)
(2)
(3)
16.(1)
(2)的最小负整数值为
17.(1);(2).
18.(1)
(2)
(3)∠A的度数是或或或
19.(1)元,元;
(2)台.
20.(1);
(2)10
(3)6
21.(1)解:理由如下:∵∠BNM=∠AND,∠AOE=∠BNM,∴∠AOE=∠AND,
∴OE∥DM;
(2)解:∵AB与底座CD都平行于地面EF,∴AB∥CD,∴∠BOD=∠ODC=30°,
∵∠AOF+∠BOD=180°,∴∠AOF=150°,
∵OE平分∠AOF,∴∠EOF=∠AOF=75°,∴∠BOE=∠BOD+∠EOF=105°,
∵OE∥DM,∴∠ANM=∠BOE=105°.
(1)先利用对顶角相等,得到 ∠BNM=∠AND ,再根据同位角相等,即 ∠AOE=∠AND ,证明两直线平行;
(2)根据平角性质,得到 ∠AOF+∠BOD=180° ,再结合题目条件,求出∠AOF=150°,又已知OE平分∠AOF , ∠ODC=30°, 算出 ∠EOF=75° ,继而可算出 ∠BOE=∠BOD+∠EOF=105° ,在利用 OE∥DM ,内错角相等,最后推出 ∠ANM=∠BOE=105° 。
22.(1)解:解:,
,
在数轴上表示如下:
故答案为:,
在数轴上表示如下:
.
(2)解:解:,解不等式①可得:,
∴
解不等式②可得:
∴,
∴不等式组的解集为;
在数轴上表示如下:
故答案为:不等式组的解集为,
在数轴上表示如下:
(1)根据解不等式的一般步骤:先移项,合并同类项,化系数为1 求出不等式的解集,然后在数轴上表示出来即可;
(2)不等式①先去括号,再解不等式,不等式②先去分母,去括号再解不等式,分别求出两个不等式的解集,根据口诀:大大取大,小小取小,大小小大中间找,大大小小找不到,再确定不等式组的解集,最后在数轴上表示出来即可.
23.解:设甲、乙两班分别有x、y人.
根据题意得
解得
故甲班有55人,乙班有48人.
设甲、乙两班分别有x、y人,根据题意列出二元一次方程组求解即可。
24.解:∵EF∥BC,
∴∠BAF=180°﹣∠B=100°,
∵AC平分∠BAF,
∴∠CAF= ∠BAF=50°,
∵EF∥BC,
∴∠C=∠CAF=50°
根据两直线平行,同旁内角互补求出∠BAF,再根据角平分线的定义求出∠CAF,然后根据两直线平行,内错角相等解答.
25.解:CD⊥AB.理由如下:
∴DG∥BC,
∴∠1=∠DCB,
∵∠1=∠2,
∴∠2=∠DCB,
∴CD∥EF,
∴∠CDB=∠EFB,
∵EF⊥AB,
∴∠EFB=90°,
∴∠CDB=90°,
∴CD⊥AB.
由平行线的性质和已知条件可证明CD∥EF,可求得∠CDB=90°,可判断CD⊥AB.
26.(1)①;(2);(3)
同课章节目录
