2024-2025学年沪科版(2024)七年级数学下册期末真题专项练习 02 填空题(含答案)
文档属性
| 名称 | 2024-2025学年沪科版(2024)七年级数学下册期末真题专项练习 02 填空题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 415.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-25 00:00:00 | ||
图片预览




文档简介
2024-2025学年沪科版(2024)七年级数学下册期末真题
专项练习 02 填空题
一、填空题
1.(2024七下·合肥期末)使等式成立的x的值为或;使等式成立的x的值为或;使等式成立的x的值为或.
根据上述材料,回答下列问题:
(1)使等式成立的x的值为 ;
(2)使等式成立的m的值为 .
2.(2024七下·合肥期末)已知关于x的分式方程的解是整数,则整数m的值是 .
3.(2024七下·灵璧期末)如图,直线a,b相交于点O,若,则 .
4.(2024七下·北辰期末)已知与的两边分别平行,且、的度数分别为、,则x的值为 .
5.(2024七下·蚌埠期末)关于的分式方程.
(1)若这个方程的解为,则的值为 ;
(2)若这个方程无解,则的值为 .
6.(2024七下·蚌埠期末)如图,直线、相交于点、平分、于点,则 .
7.(2024七下·蚌埠期末)已知的算术平方根是,是的立方根,则 .
8.(2024七下·蚌埠期末)分解因式: .
9.(2024八下·永寿期末)若关于x的不等式的正整数解是1,2,3,4,则整数a的最小值是 .
10.(2024七下·淮北期末)定义:是以a,b,c为系数的二次多项式,即,其中a,b,c均为实数,例如,,则.
(1)当时, .
(2)若,则 .
11.(2024七下·凤阳期末)比较大小: (填“>”“<”或“=”).
12.(2024七下·潜山期末)如图,直线,相交于点O,平分.
(1)若,则 (用含的式子表示);
(2)若,,则 .
13.(2024七下·天长期末)如图,直线AB,CD相交于点,,,则 °.
14.(2024七下·安徽期末)某种商品的进价为600元,出售时标价为900元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于,则最低可打 折.
15.(2024七下·蜀山期末)凸透镜成像是自然界中的一个基本现象,其中物距记为u,像距记为v,透镜焦距记为f,三者满足关系式:,若已知u、f,则v= .
16.(2024七下·马鞍山期末)如图所示为一个计算程序,若输入的值为4,则输出的结果应为 .
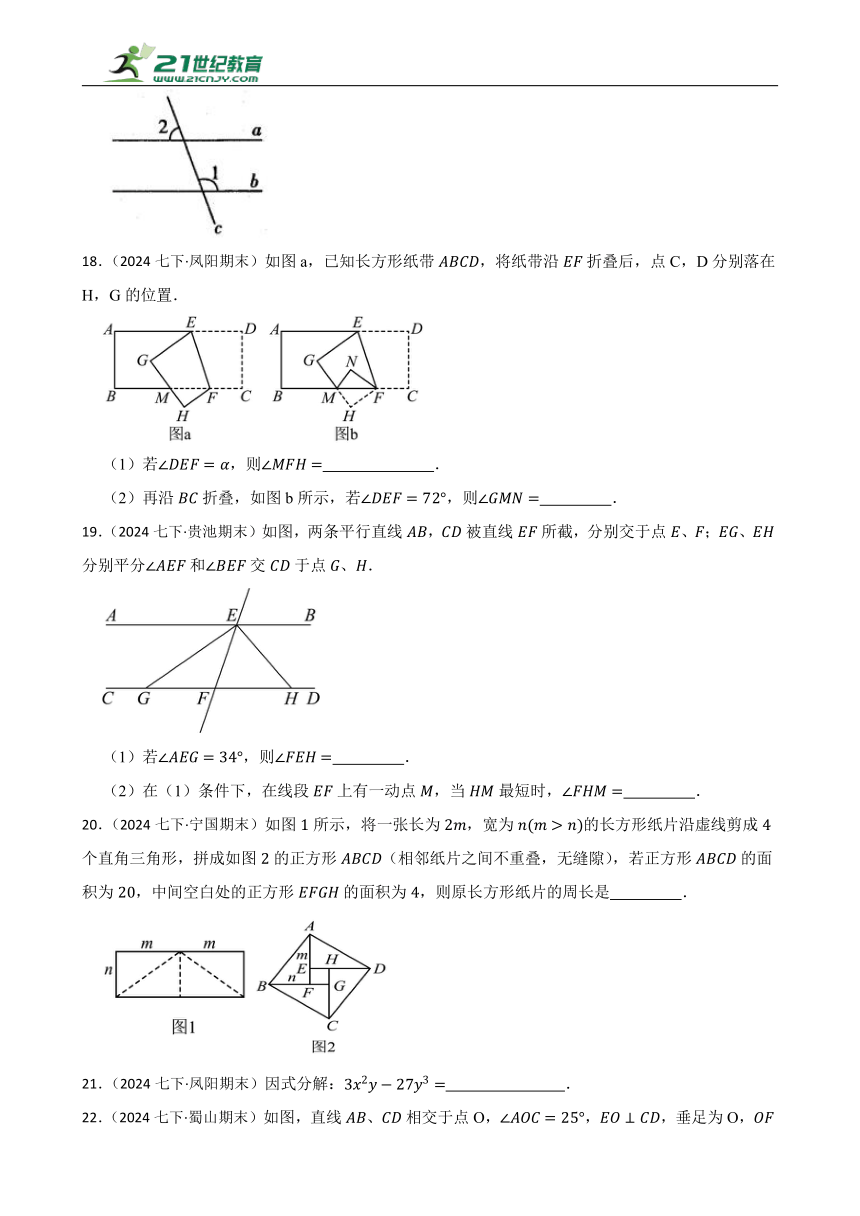
17.(2024七下·霍邱期末)如图,直线被直线c所截,若,,则 .
18.(2024七下·凤阳期末)如图a,已知长方形纸带,将纸带沿折叠后,点C,D分别落在H,G的位置.
(1)若,则 .
(2)再沿折叠,如图b所示,若,则 .
19.(2024七下·贵池期末)如图,两条平行直线,被直线所截,分别交于点、;、分别平分和交于点、.
(1)若,则 .
(2)在(1)条件下,在线段上有一动点,当最短时, .
20.(2024七下·宁国期末)如图所示,将一张长为,宽为的长方形纸片沿虚线剪成个直角三角形,拼成如图的正方形(相邻纸片之间不重叠,无缝隙),若正方形的面积为,中间空白处的正方形的面积为,则原长方形纸片的周长是 .
21.(2024七下·凤阳期末)因式分解: .
22.(2024七下·蜀山期末)如图,直线、相交于点O,,,垂足为O,平分,则 .
23.(2023七下·太和期末)若关于x,y的二元一次方程组的解满足不等式,则的取值范围是 .
24.(2024七下·天长期末)已知关于x的分式方程.
(1)当时,方程的根是 ;
(2)若该方程的解是非负数,且满足,则所有满足条件的偶数的值之和为 .
25.(2024七下·芜湖期末)我国著名数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:一个数是59319,希望求它的立方根.华罗庚脱口而出:39.邻座的乘客十分惊奇,忙问计算的奥妙.
你知道华罗庚是怎样迅速准确地计算出来的吗?可以按如下步骤思考:
第1步:确定的位数.因为,,,所以是2位数;
第2步:确定个位数字.因为59319的个位上的数是9,,所以的个位上的数是9;
第3步:确定十位数字.划去59319后面的三位319得到数59,,,而,由此能确定的十位上的数是3.
综合以上可得.
已知103823是整数的立方,按照上述方法,它的立方根是 .
26.(2024七下·蜀山期末)如图,,点E,F分别在直线,上,点P在,之间,若,,那么 .
27.(2024七下·芜湖期末)如图①是自行车的实物图,图②是它的部分示意图,,点在上,,,.则的度数为 .
28.(2024七下·舒城期末)如图和均为直角三角形,将其直角顶点放在一起,其中,,.若不动,绕顶点转动一周,当时, .
29.(2024七下·太湖期末)已知:,点C在点D的右侧,平分,平分,所在直线交于点E,.
(1) ;
(2)若,则的度数是 (用含n的式子表示)
30.(2024七下·马鞍山期末)若不等式组的解集为,那么的值等于 .
31.(2024七下·潜山期末)分解因式: .
32.(2024七下·太湖期末)如图,边长分别为a、b的两个正方形并排放在一起,当,,时阴影部分的面积为 .
33.(2024七下·马鞍山期末)若关于x的分式方程无解,则m的值为 .
34.(2024七下·大观期末)已知甲、乙两个长方形,它们的边长如图(m为正整数),甲、乙的面积分别为.
(1)与的大小关系为: ;(用“>”、“<”、“=”填空)
(2)若满足条件的整数n有且只有3个,则m的值为 .
35.(2024七下·潜山期末)要使的展开式中不含项,则m的值为 .
36.(2024七下·无为期末)定义表示不大于x的最大整数,例如:,,.有下列结论:①当时,的值为1;②;③;④是方程的唯一解,其中,正确的有 .(填序号)
37.(2024七下·霍邱期末)若关于x的不等式组有且只有2个整数解,则a的取值范围是 .
38.(2024七下·安徽期末)已知,如图平行,O为平面内一点,,的角平分线相交于G点,则 °
39.(2024七下·天长期末)已知,,则 .
40.(2024七下·舒城期末)若数a使关于x的分式方程的解为非负数,则a的取值正确的是 .
41.(2024七下·大观期末)若关于的方程的解为正数,则的取值范围是 .
42.(2024七下·安徽期末)若关于x的分式方程 +2= 的解为正数,则k的取值范围是 .
43.(2024七下·大观期末)分式有意义时,x的取值范围是 .
44.(2024七下·灵璧期末)如图,有两个正方形A,B,将A,B并列放置后构造新的图形,分别得到长方形图1与正方形图2.若图1、图2中阴影的面积分别为14与36,则正方形B的面积为 .
45.(2024七下·淮北期末)某种花粉的直径约为0.0000084m,数据0.0000084用科学记数法表示为 .
46.(2024七下·乾安期末)如图,一条公路修在湖边时,需要拐弯绕道而过,第一次的拐角,第二次的拐角,第三次的拐角是,这时的道路恰好和第一次拐弯之前的道路平行,则的度数为 .
47.(2024七下·宁国期末)如图,已知,,,,若;则 度.
48.(2024七下·宁国期末)若关于的不等式恰有3个正整数解,则的取值范围是 .
49.(2024七下·利辛期末)若有意义,则的取值范围是 .
50.(2024七下·贵池期末)已知,则的值是 .
答案解析部分
1.或;或
2.1或3或4
3.
4.14或40
5.5;3或7
6.
7.
8.
9.
10.;
11.<
12.;或
13.
14.7
15.
16.
17.
18.;
19.;
20.20
21.
22.
23.
解方程组,
②-①,得:x-y=4k,
又∵x-y>-1,
∴4k>-1,
∴k>.
直接用②-①,可得x-y=4k,然后得出4k>-1,解不等式,即可求得k的取值范围。
24.;
25.47
26.30或90
27.
28.或
29.;
30.
31.
解:2x3-8xy2=2x(x2-4y2)=2x(x+2y)(x-2y)。
故第1空答案为:2x(x+2y)(x-2y)。
先根据提公因式法因式分解,提出公因式2x,再根据平方差公式进一步分解,即可得出最后结果。
32.17
33.或或
34.>;1011
35.
解:=2x3+mx2-4x+6x2+3mx-12=2x3+(m+6)x2+(3m-4)x-12,
∵展开式中不含项 ,
∴m+6=0,
∴m=-6.
故第1空答案为:-6.
根据多项式乘多项式法则,得出多项式相乘所得的积为2x3+(m+6)x2+(3m-4)x-12,再根据展开式不含二次项,可得二次项系数为0,从而得到m=-6.
36.①②③
37.
38.或
39.
40.且
41.且
42.k< 且k≠﹣
解:
方程两边同乘(x-1)得,1+2x-2=-2k,
解得
∵方程的解为正数
∴ 且
∴ 且
故答案为: 且 .
先利用分式方程的解法求出解,再根据题意列出不等式求解即可。
43.
44.4
45.
46.
47.
48.
解:∵不等式 ,
∴-x≥-5-m,
∴x≤5+m,
∵关于的不等式恰有3个正整数解,
∴3≤5+m<4,
解得:,
故答案为:.
利用不等式的性质求出x≤5+m,再求出3≤5+m<4,最后求解即可。
49.
50.
专项练习 02 填空题
一、填空题
1.(2024七下·合肥期末)使等式成立的x的值为或;使等式成立的x的值为或;使等式成立的x的值为或.
根据上述材料,回答下列问题:
(1)使等式成立的x的值为 ;
(2)使等式成立的m的值为 .
2.(2024七下·合肥期末)已知关于x的分式方程的解是整数,则整数m的值是 .
3.(2024七下·灵璧期末)如图,直线a,b相交于点O,若,则 .
4.(2024七下·北辰期末)已知与的两边分别平行,且、的度数分别为、,则x的值为 .
5.(2024七下·蚌埠期末)关于的分式方程.
(1)若这个方程的解为,则的值为 ;
(2)若这个方程无解,则的值为 .
6.(2024七下·蚌埠期末)如图,直线、相交于点、平分、于点,则 .
7.(2024七下·蚌埠期末)已知的算术平方根是,是的立方根,则 .
8.(2024七下·蚌埠期末)分解因式: .
9.(2024八下·永寿期末)若关于x的不等式的正整数解是1,2,3,4,则整数a的最小值是 .
10.(2024七下·淮北期末)定义:是以a,b,c为系数的二次多项式,即,其中a,b,c均为实数,例如,,则.
(1)当时, .
(2)若,则 .
11.(2024七下·凤阳期末)比较大小: (填“>”“<”或“=”).
12.(2024七下·潜山期末)如图,直线,相交于点O,平分.
(1)若,则 (用含的式子表示);
(2)若,,则 .
13.(2024七下·天长期末)如图,直线AB,CD相交于点,,,则 °.
14.(2024七下·安徽期末)某种商品的进价为600元,出售时标价为900元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于,则最低可打 折.
15.(2024七下·蜀山期末)凸透镜成像是自然界中的一个基本现象,其中物距记为u,像距记为v,透镜焦距记为f,三者满足关系式:,若已知u、f,则v= .
16.(2024七下·马鞍山期末)如图所示为一个计算程序,若输入的值为4,则输出的结果应为 .
17.(2024七下·霍邱期末)如图,直线被直线c所截,若,,则 .
18.(2024七下·凤阳期末)如图a,已知长方形纸带,将纸带沿折叠后,点C,D分别落在H,G的位置.
(1)若,则 .
(2)再沿折叠,如图b所示,若,则 .
19.(2024七下·贵池期末)如图,两条平行直线,被直线所截,分别交于点、;、分别平分和交于点、.
(1)若,则 .
(2)在(1)条件下,在线段上有一动点,当最短时, .
20.(2024七下·宁国期末)如图所示,将一张长为,宽为的长方形纸片沿虚线剪成个直角三角形,拼成如图的正方形(相邻纸片之间不重叠,无缝隙),若正方形的面积为,中间空白处的正方形的面积为,则原长方形纸片的周长是 .
21.(2024七下·凤阳期末)因式分解: .
22.(2024七下·蜀山期末)如图,直线、相交于点O,,,垂足为O,平分,则 .
23.(2023七下·太和期末)若关于x,y的二元一次方程组的解满足不等式,则的取值范围是 .
24.(2024七下·天长期末)已知关于x的分式方程.
(1)当时,方程的根是 ;
(2)若该方程的解是非负数,且满足,则所有满足条件的偶数的值之和为 .
25.(2024七下·芜湖期末)我国著名数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:一个数是59319,希望求它的立方根.华罗庚脱口而出:39.邻座的乘客十分惊奇,忙问计算的奥妙.
你知道华罗庚是怎样迅速准确地计算出来的吗?可以按如下步骤思考:
第1步:确定的位数.因为,,,所以是2位数;
第2步:确定个位数字.因为59319的个位上的数是9,,所以的个位上的数是9;
第3步:确定十位数字.划去59319后面的三位319得到数59,,,而,由此能确定的十位上的数是3.
综合以上可得.
已知103823是整数的立方,按照上述方法,它的立方根是 .
26.(2024七下·蜀山期末)如图,,点E,F分别在直线,上,点P在,之间,若,,那么 .
27.(2024七下·芜湖期末)如图①是自行车的实物图,图②是它的部分示意图,,点在上,,,.则的度数为 .
28.(2024七下·舒城期末)如图和均为直角三角形,将其直角顶点放在一起,其中,,.若不动,绕顶点转动一周,当时, .
29.(2024七下·太湖期末)已知:,点C在点D的右侧,平分,平分,所在直线交于点E,.
(1) ;
(2)若,则的度数是 (用含n的式子表示)
30.(2024七下·马鞍山期末)若不等式组的解集为,那么的值等于 .
31.(2024七下·潜山期末)分解因式: .
32.(2024七下·太湖期末)如图,边长分别为a、b的两个正方形并排放在一起,当,,时阴影部分的面积为 .
33.(2024七下·马鞍山期末)若关于x的分式方程无解,则m的值为 .
34.(2024七下·大观期末)已知甲、乙两个长方形,它们的边长如图(m为正整数),甲、乙的面积分别为.
(1)与的大小关系为: ;(用“>”、“<”、“=”填空)
(2)若满足条件的整数n有且只有3个,则m的值为 .
35.(2024七下·潜山期末)要使的展开式中不含项,则m的值为 .
36.(2024七下·无为期末)定义表示不大于x的最大整数,例如:,,.有下列结论:①当时,的值为1;②;③;④是方程的唯一解,其中,正确的有 .(填序号)
37.(2024七下·霍邱期末)若关于x的不等式组有且只有2个整数解,则a的取值范围是 .
38.(2024七下·安徽期末)已知,如图平行,O为平面内一点,,的角平分线相交于G点,则 °
39.(2024七下·天长期末)已知,,则 .
40.(2024七下·舒城期末)若数a使关于x的分式方程的解为非负数,则a的取值正确的是 .
41.(2024七下·大观期末)若关于的方程的解为正数,则的取值范围是 .
42.(2024七下·安徽期末)若关于x的分式方程 +2= 的解为正数,则k的取值范围是 .
43.(2024七下·大观期末)分式有意义时,x的取值范围是 .
44.(2024七下·灵璧期末)如图,有两个正方形A,B,将A,B并列放置后构造新的图形,分别得到长方形图1与正方形图2.若图1、图2中阴影的面积分别为14与36,则正方形B的面积为 .
45.(2024七下·淮北期末)某种花粉的直径约为0.0000084m,数据0.0000084用科学记数法表示为 .
46.(2024七下·乾安期末)如图,一条公路修在湖边时,需要拐弯绕道而过,第一次的拐角,第二次的拐角,第三次的拐角是,这时的道路恰好和第一次拐弯之前的道路平行,则的度数为 .
47.(2024七下·宁国期末)如图,已知,,,,若;则 度.
48.(2024七下·宁国期末)若关于的不等式恰有3个正整数解,则的取值范围是 .
49.(2024七下·利辛期末)若有意义,则的取值范围是 .
50.(2024七下·贵池期末)已知,则的值是 .
答案解析部分
1.或;或
2.1或3或4
3.
4.14或40
5.5;3或7
6.
7.
8.
9.
10.;
11.<
12.;或
13.
14.7
15.
16.
17.
18.;
19.;
20.20
21.
22.
23.
解方程组,
②-①,得:x-y=4k,
又∵x-y>-1,
∴4k>-1,
∴k>.
直接用②-①,可得x-y=4k,然后得出4k>-1,解不等式,即可求得k的取值范围。
24.;
25.47
26.30或90
27.
28.或
29.;
30.
31.
解:2x3-8xy2=2x(x2-4y2)=2x(x+2y)(x-2y)。
故第1空答案为:2x(x+2y)(x-2y)。
先根据提公因式法因式分解,提出公因式2x,再根据平方差公式进一步分解,即可得出最后结果。
32.17
33.或或
34.>;1011
35.
解:=2x3+mx2-4x+6x2+3mx-12=2x3+(m+6)x2+(3m-4)x-12,
∵展开式中不含项 ,
∴m+6=0,
∴m=-6.
故第1空答案为:-6.
根据多项式乘多项式法则,得出多项式相乘所得的积为2x3+(m+6)x2+(3m-4)x-12,再根据展开式不含二次项,可得二次项系数为0,从而得到m=-6.
36.①②③
37.
38.或
39.
40.且
41.且
42.k< 且k≠﹣
解:
方程两边同乘(x-1)得,1+2x-2=-2k,
解得
∵方程的解为正数
∴ 且
∴ 且
故答案为: 且 .
先利用分式方程的解法求出解,再根据题意列出不等式求解即可。
43.
44.4
45.
46.
47.
48.
解:∵不等式 ,
∴-x≥-5-m,
∴x≤5+m,
∵关于的不等式恰有3个正整数解,
∴3≤5+m<4,
解得:,
故答案为:.
利用不等式的性质求出x≤5+m,再求出3≤5+m<4,最后求解即可。
49.
50.
同课章节目录
