2024-2025学年沪科版(2024)七年级数学下册期末真题专项练习 04 解答题(含答案)
文档属性
| 名称 | 2024-2025学年沪科版(2024)七年级数学下册期末真题专项练习 04 解答题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 390.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-25 05:07:56 | ||
图片预览



文档简介
2024-2025学年沪科版(2024)七年级数学下册期末真题
专项练习 04 解答题
一、解答题
1.(2024七下·安徽期末)阅读与思考
整式乘法与因式分解是方向相反的变形. 得. 利用这个式子可以将某些二次项系数是1的二次三项式进行因式分解,我们把这种方法称为“十字相乘法”. 例如:将式子分解因式. 解:.
请仿照上面的方法,解答下列问题:
(1)分解因式:.
(2)分解因式:.
(3)若可分解为两个一次因式的积,求整数p所有可能的值.
2.(2024七下·马鞍山期末)完全平方公式经过适当的变形,可以解决很多数学问题.
(1)若,,求的值.
(2)若,求的值.
(3)根据上面的解题思路与方法解决下列题:如图,是线段上的一点,以,为边向两边作正方形,设,两正方形的面积和为20,求的面积.
3.(2024七下·六安期末)年,贵州省出台“引客人黔”团队旅游及营销奖励办法,助推旅游市场强劲复苏.某旅行社5月1日租住某景区A、B两种客房一天下面是有关信息:用元租到A客房的数量与用元租到B客房的数量相等.已知每间A客房的单价比每间B客房的单价多元.
(1)求A,B两种客房的单价分别是多少;
(2)若租住A,B两种客房共间,A客房的数量不低于B客房数量的,且所花总费用不高于元,求有哪几种租住方案.
4.(2024七下·界首期末)超市分两次购进甲、乙两种商品若干件,进货总价如下表:
甲 乙
第一次 1200元 900元
第二次 总共不超过1262元
(1)第一次购进甲商品件数是乙商品件数的2倍,且甲商品的单价比乙商品的单价便宜10元/件,求甲商品的单价;
(2)第二次共购进50件,两种商品的单价与第一次相比,甲提高了10%,乙降价了10%,问此次最多购进乙商品多少件?
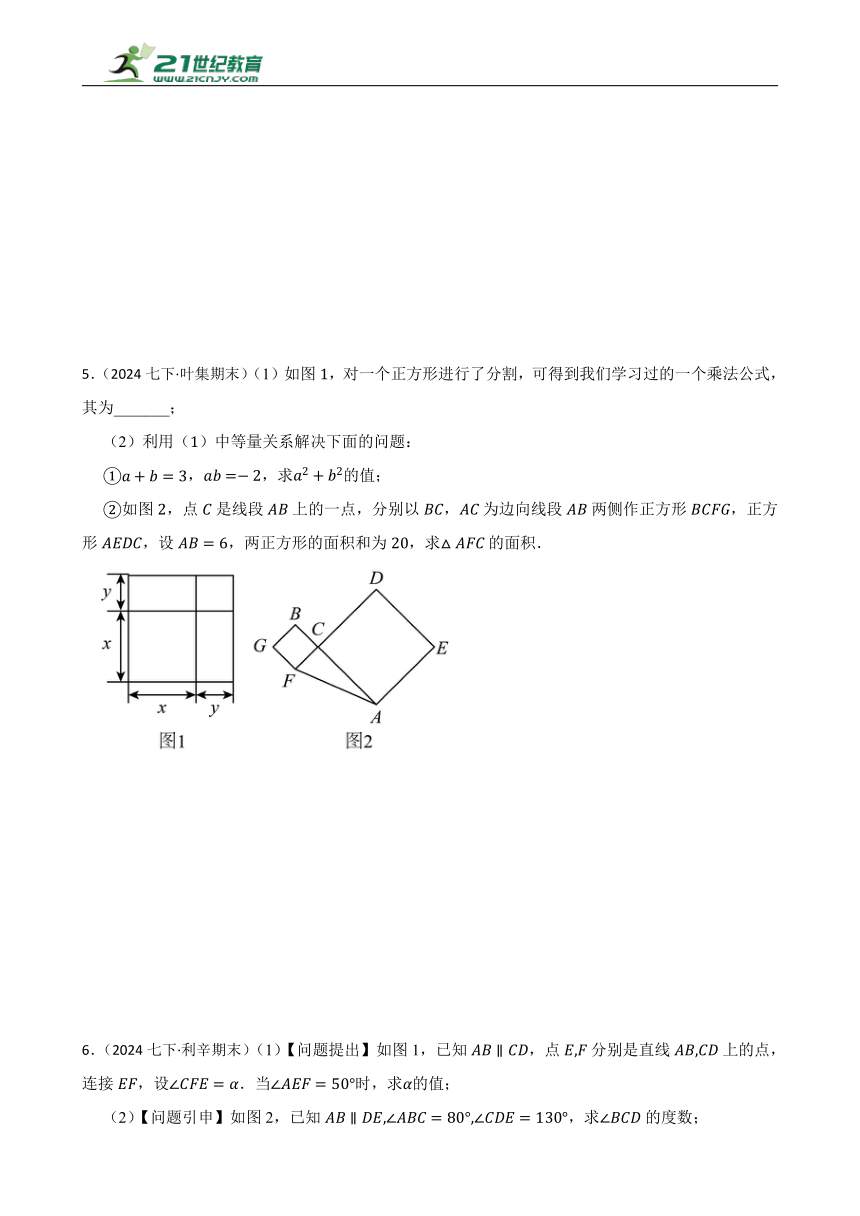
5.(2024七下·叶集期末)(1)如图,对一个正方形进行了分割,可得到我们学习过的一个乘法公式,其为_______;
(2)利用()中等量关系解决下面的问题:
,,求的值;
如图,点是线段上的一点,分别以,为边向线段两侧作正方形,正方形,设,两正方形的面积和为,求的面积.
6.(2024七下·利辛期末)(1)【问题提出】如图1,已知,点分别是直线上的点,连接,设.当时,求的值;
(2)【问题引申】如图2,已知,求的度数;
(3)【问题拓展】如图3,已知平分平分.若,求的度数.
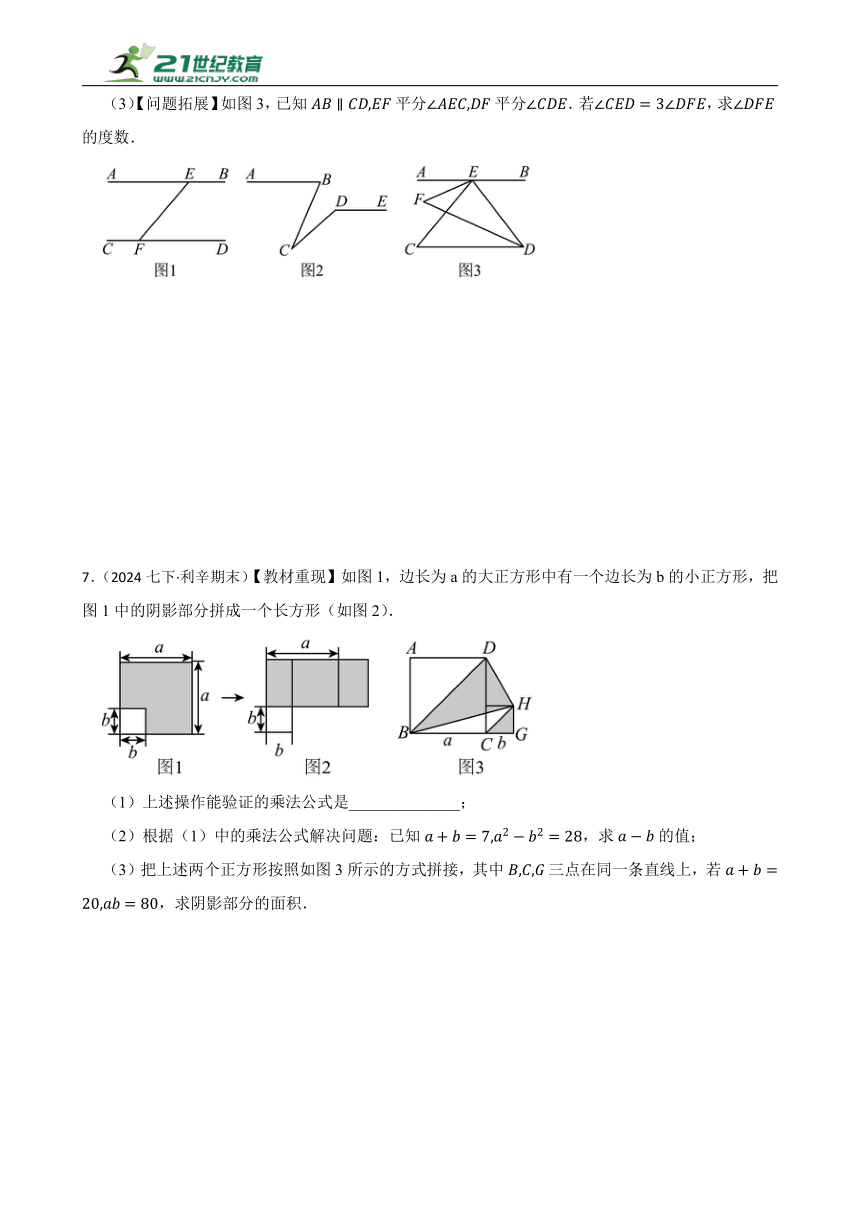
7.(2024七下·利辛期末)【教材重现】如图1,边长为a的大正方形中有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2).
(1)上述操作能验证的乘法公式是______________;
(2)根据(1)中的乘法公式解决问题:已知,求的值;
(3)把上述两个正方形按照如图3所示的方式拼接,其中三点在同一条直线上,若,求阴影部分的面积.
8.(2024七下·利辛期末)如图,已知直线与直线相交于点,.
(1)若,求的度数;
(2)若,平分,求的度数.
9.(2024七下·淮北期末)我们把符号“”称为二阶行列式,规定它的运算法则为,例如,.
(1)求不等式的解集;
(2)若关于x的不等式的解都是(1)中不等式的解,求n的取值范围.
10.(2024七下·淮北期末)如图所示的是某大院窗格的一部分,其中“O”代表窗格上所贴的剪纸,设第x个窗格上所贴“O”的个数为y.
(1)填写下表.
x 1 2 3 4 5 x
y 5 8 11
17 (用含x的式子表示)
(2)若第x个窗格上所贴的“O”的个数大于50,求x的取值范围.
11.(2024七下·凤阳期末)如图,,点A为直线上一定点,B为直线上的动点,在直线与之间且在线段的右方作点D,使得,设(为锐角).
(1)求的值;
(2)当点B在直线上运动的过程中,若平分,也恰好平分,请求出此时的值.
12.(2024七下·寿县期末)解不等式:.
13.(2024七下·安徽期末)已知,关于x的分式方程.
(1)当,时,求分式方程的解;
(2)当时,求b为何值时分式方程无解;
(3)若,且a、b为正整数,当分式方程的解为整数时,求b的值.
14.(2024七下·安徽期末)两个边长分别为和的正方形如图放置图,其未叠合部分阴影面积为;若再在图中大正方形的右下角摆放一个边长为的小正方形如图,两个小正方形叠合部分阴影面积为.
(1)用含,的代数式分别表示、;
(2)若,,求的值.
15.(2024七下·合肥期末)如图1,已知,将一块含角的直角三角板按如图所示放置(),使顶点B落在边上,绕点B转动三角板,始终保持点C在的上方,过点C作.
(1)当___________°时,.
(2)如图2,作的角平分线.
(ⅰ)若,求的度数,
(ⅱ)将三角板绕点B转动,当三角板有一边与垂直时,求的度数.(直接写出答案)
16.(2024七下·合肥期末)如图,学校有一块边长为米的正方形空地,计划在阴影部分的地方进行绿化,搭建一个小花坛,中间修建一个长为米、宽为b米的鱼池供观赏.
(1)求绿化的面积是多少平方米?
(2)若,时,求绿化面积、
17.(2024七下·贵池期末)我们知道,是一个无理数,将这个数减去整数部分,差就是小数部分,即的整数部分是1,小数部分是,请回答以下问题:
(1)的小数部分是______,的小数部分是______;
(2)若,其中是整数,且,求与的值.
18.(2024七下·太湖期末)若x满足,求的值.
解:设,
则,
∴.
请仿照上面的方法求解下面问题:
(1)若x满足,求的值;
(2)已知正方形的边长为x,E,F分别是上的点,且,长方形的面积是48,分别作正方形和正方形,求阴影部分的面积.
19.(2024七下·太湖期末)已知ABCD,点E在AB与CD之间.
(1)图1中,试说明:∠BED=∠ABE+∠CDE;
(2)图2中,∠ABE的平分线与∠CDE的平分线相交于点F,请利用(1)的结论说明:∠BED=2∠BFD.
(3)图3中,∠ABE的平分线与∠CDE的平分线相交于点F,请直接写出∠BED与∠BFD之间的数量关系.
20.(2024七下·霍邱期末)梅雨季节即将来临,某防汛指挥部在某水域一危险地带的两岸各安置了一盏探照灯,便于夜间察看河水及两岸河堤的情况,如图1,探照灯A射出的光束自顺时针旋转至便立即回转,探照灯B射出的光束自顺时针旋转至便立即回转,两灯不停交叉照射巡视.若探照灯A射出的光束的转动速度是/秒,探照灯B射出的光束的转动速度是/秒,且,满足,假定这一带水域两岸河堤是平行的,即,且.
(1)求,的值.
(2)如图2,两探照灯同时转动,在探照灯A射出的光束首次到达之前,两探照灯射出的光束交于点C.
①过点C作,请写出与的位置关系:________,依据:________________
②若,求的度数.
(3)若探照灯B射出的光束先转动40秒,探照灯A射出的光束才开始转动,在探照灯B射出的光束第一次到达之前,当两探照灯的光束互相平行时,请直接写出探照灯A转动的时间:________.
21.(2024七下·霍邱期末)现有如图1的8张大小形状相同的直角三角形纸片,三边长分别是.用其中4张纸片拼成如图2的大正方形(空白部分是边长分别为和的正方形);用另外4张纸片拼成如图3的大正方形(中间的空白部分是边长为的正方形).
(1)观察:从整体看,图2和图3的大正方形的边长都为,所以图2和图3的大正方形的面积都可以表示为,记为结论①.由于整个图形的面积等于各部分面积的和,所以图2中的大正方形的面积又可以用含字母a、b的代数式表示为: ________,记为结论②;
同样,图3中的大正方形的面积又可以用含字母a、b、c的代数式表示为:________,记为结论③.
(2)思考:
由结论①和结论②,可以得到等式________________
由结论②和结论③,可以得到等式________________
(3)应用:若分别以直角三角形三边为直径,向外作半圆(如图4),三个半圆的面积分别记作、、,且,求的值.
22.(2024七下·宁国期末)某水果商两次去批发市场采购同一种水果,第一次用2000元购进了若干千克,很快卖完,第二次用3000元所购数量比第一次多100千克,且每千克的进价比第一次提高了20%.
(1)求第一次购买水果的进价;
(2)求第二次购买水果的数量:
(3)该水果商按以下方案卖出第二批的水果:先以元/千克的价格售出千克,再以8元/千克的价格售出剩余的全部水果,共获利1600元.若,均为整数,且不超过第二次进价的2倍,求和的值.
23.(2024七下·民勤期末)已知的立方根是2,的算术平方根是4,c是的整数部分.
(1)求a,b,c的值;
(2)求的平方根.
24.(2023七下·迎江期末)阅读下面的文字,解答问题:
大家知道是无理数,而无理数是无限不循环小数,的小数部分我们不可能全部地写出来,于是小明用来表示的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:
∵,即,
∴的整数部分为2,小数部分为.
请解答:
(1)的整数部分是 ,小数部分是 .
(2)如果的小数部分为a,的整数部分为b,求的值;
(3)已知:,其中x是整数,,求的相反数.
25.(2022七下·宜春期末)阅读下面的材料:
对于实数,我们定义符号的意义为:当时,;当时,,如:.
根据上面的材料回答下列问题:
(1)______;
(2)当时,求x的取值范围.
26.(2023七下·怀远期末)某学校2021年在某商场购买甲、乙两种不同的足球,购买甲种足球共花费4000元,购买乙种足球共花费2800元,购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元;
(1)求购买一个甲种足球、一个乙种足球各需多少元;
(2)2022年这所学校决定再次购买甲、乙两种足球共50个.恰逢该商场对两种足球的售价进行调整,甲种足球售价比第一次购买时提高了10%,乙种足球售价比第一次购买时降低了10%.如果此次购买甲、乙两种足球的总费用不超过2910元,那么这所学校最多可购买多少个乙种足球?
27.(2023七下·瑶海期末)中国是最早发现并利用茶的国家,形成了具有独特魅力的茶文化2020年5月21日以“茶和世界共品共享”为主题的第一届国际茶日在中国召开.某茶店用4000元购进了A种茶叶若干盒,用8400元购进B种茶叶若干盒,所购B种茶叶比A种茶叶多10盒,且B种茶叶每盒进价是A种茶叶每盒进价的1.4倍.
(1)A,B两种茶叶每盒进价分别为多少元?
(2)第一次所购茶叶全部售完后第二次购进A,B两种茶叶共100盒(进价不变),A种茶叶的售价是每盒300元,B种茶叶的售价是每盒400元.两种茶叶各售出一半后,为庆祝国际茶日,两种茶叶均打七折销售,全部售出后,第二次所购茶叶的利润为5800元(不考虑其他因素),求本次购进A,B两种茶叶各多少盒?
28.(2023七下·迎江期末)已知关于x的方程
(1)当时,求方程的解;
(2)当m取何值时,此方程无解;
(3)当此方程的解是正数时,求m的取值范围.
答案解析部分
1.(1)解:原式
;
(2)解:原式
(3)解:∵,
∴或或或
因此整数p的值可能为5或或1或.
(1)直接根据"十字相乘法"分解因式,即可得出结果;
(2)先提公因式x,再用十字相乘法进行因式分解,即可得出结果;
(3)先把常数项-6分解成两个因数的积,写出所有可能的结果,然后把两个因数相加,就可得出p所有可能的值。
2.(1)7
(2)7
(3)4
3.(1)A,B两种客房的单价分别是元,元
(2)有3种方案,分别为:
方案1:租住客房间,则租住客房间;
方案2:租住客房间,则租住客房间;
方案3:租住客房间,则租住客房间
4.(1)甲商品的单价为20元;(2)此次最多购进乙商品32件
5.();();.
6.(1)(2)(3)
7.(1)
(2)4
(3)120
8.(1)
(2)
9.(1)
(2)
10.(1)14,
(2).
11.(1)90°
(2)30°
12..
13.(1)
(2)
(3)3、29、55、185
14.(1),
(2)
15.(1)
(2)(ⅰ)(ⅱ)或或
16.(1)平方米
(2)平方米
17.(1),;
(2)10,.
18.(1)11;(2)28.
19.(1)∠BED=∠ABE+∠CDE
(2)∠BED=2∠BFD
(3)∠BED=360°-2∠BFD
20.(1)
(2)①平行,如果两条直线和第三条直线平行,那么这两条直线平行;②
(3)秒或秒
21.(1),
(2),
(3)
22.(1)第一次购买水果的进价为5元/千克
(2)第二次购买水果的数量为500千克
(3)当a的值为12时,m的值为150;当a的值为11时,m的值为200;当a的值为10时,m的值为300
23.(1),,
(2)
24.(1)4,
(2)
(3)
25.(1)﹣1 ;(2)x≥
26.(1)一个甲种足球需50元,一个乙种足球需70元;
(2)这所学校最多可购买20个乙种足球
27.(1)A,B两种茶叶每盒进价分别为200元,280元;(2)第二次购进A种茶叶40盒,B种茶叶60盒
28.(1);
(2);
(3)且
专项练习 04 解答题
一、解答题
1.(2024七下·安徽期末)阅读与思考
整式乘法与因式分解是方向相反的变形. 得. 利用这个式子可以将某些二次项系数是1的二次三项式进行因式分解,我们把这种方法称为“十字相乘法”. 例如:将式子分解因式. 解:.
请仿照上面的方法,解答下列问题:
(1)分解因式:.
(2)分解因式:.
(3)若可分解为两个一次因式的积,求整数p所有可能的值.
2.(2024七下·马鞍山期末)完全平方公式经过适当的变形,可以解决很多数学问题.
(1)若,,求的值.
(2)若,求的值.
(3)根据上面的解题思路与方法解决下列题:如图,是线段上的一点,以,为边向两边作正方形,设,两正方形的面积和为20,求的面积.
3.(2024七下·六安期末)年,贵州省出台“引客人黔”团队旅游及营销奖励办法,助推旅游市场强劲复苏.某旅行社5月1日租住某景区A、B两种客房一天下面是有关信息:用元租到A客房的数量与用元租到B客房的数量相等.已知每间A客房的单价比每间B客房的单价多元.
(1)求A,B两种客房的单价分别是多少;
(2)若租住A,B两种客房共间,A客房的数量不低于B客房数量的,且所花总费用不高于元,求有哪几种租住方案.
4.(2024七下·界首期末)超市分两次购进甲、乙两种商品若干件,进货总价如下表:
甲 乙
第一次 1200元 900元
第二次 总共不超过1262元
(1)第一次购进甲商品件数是乙商品件数的2倍,且甲商品的单价比乙商品的单价便宜10元/件,求甲商品的单价;
(2)第二次共购进50件,两种商品的单价与第一次相比,甲提高了10%,乙降价了10%,问此次最多购进乙商品多少件?
5.(2024七下·叶集期末)(1)如图,对一个正方形进行了分割,可得到我们学习过的一个乘法公式,其为_______;
(2)利用()中等量关系解决下面的问题:
,,求的值;
如图,点是线段上的一点,分别以,为边向线段两侧作正方形,正方形,设,两正方形的面积和为,求的面积.
6.(2024七下·利辛期末)(1)【问题提出】如图1,已知,点分别是直线上的点,连接,设.当时,求的值;
(2)【问题引申】如图2,已知,求的度数;
(3)【问题拓展】如图3,已知平分平分.若,求的度数.
7.(2024七下·利辛期末)【教材重现】如图1,边长为a的大正方形中有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2).
(1)上述操作能验证的乘法公式是______________;
(2)根据(1)中的乘法公式解决问题:已知,求的值;
(3)把上述两个正方形按照如图3所示的方式拼接,其中三点在同一条直线上,若,求阴影部分的面积.
8.(2024七下·利辛期末)如图,已知直线与直线相交于点,.
(1)若,求的度数;
(2)若,平分,求的度数.
9.(2024七下·淮北期末)我们把符号“”称为二阶行列式,规定它的运算法则为,例如,.
(1)求不等式的解集;
(2)若关于x的不等式的解都是(1)中不等式的解,求n的取值范围.
10.(2024七下·淮北期末)如图所示的是某大院窗格的一部分,其中“O”代表窗格上所贴的剪纸,设第x个窗格上所贴“O”的个数为y.
(1)填写下表.
x 1 2 3 4 5 x
y 5 8 11
17 (用含x的式子表示)
(2)若第x个窗格上所贴的“O”的个数大于50,求x的取值范围.
11.(2024七下·凤阳期末)如图,,点A为直线上一定点,B为直线上的动点,在直线与之间且在线段的右方作点D,使得,设(为锐角).
(1)求的值;
(2)当点B在直线上运动的过程中,若平分,也恰好平分,请求出此时的值.
12.(2024七下·寿县期末)解不等式:.
13.(2024七下·安徽期末)已知,关于x的分式方程.
(1)当,时,求分式方程的解;
(2)当时,求b为何值时分式方程无解;
(3)若,且a、b为正整数,当分式方程的解为整数时,求b的值.
14.(2024七下·安徽期末)两个边长分别为和的正方形如图放置图,其未叠合部分阴影面积为;若再在图中大正方形的右下角摆放一个边长为的小正方形如图,两个小正方形叠合部分阴影面积为.
(1)用含,的代数式分别表示、;
(2)若,,求的值.
15.(2024七下·合肥期末)如图1,已知,将一块含角的直角三角板按如图所示放置(),使顶点B落在边上,绕点B转动三角板,始终保持点C在的上方,过点C作.
(1)当___________°时,.
(2)如图2,作的角平分线.
(ⅰ)若,求的度数,
(ⅱ)将三角板绕点B转动,当三角板有一边与垂直时,求的度数.(直接写出答案)
16.(2024七下·合肥期末)如图,学校有一块边长为米的正方形空地,计划在阴影部分的地方进行绿化,搭建一个小花坛,中间修建一个长为米、宽为b米的鱼池供观赏.
(1)求绿化的面积是多少平方米?
(2)若,时,求绿化面积、
17.(2024七下·贵池期末)我们知道,是一个无理数,将这个数减去整数部分,差就是小数部分,即的整数部分是1,小数部分是,请回答以下问题:
(1)的小数部分是______,的小数部分是______;
(2)若,其中是整数,且,求与的值.
18.(2024七下·太湖期末)若x满足,求的值.
解:设,
则,
∴.
请仿照上面的方法求解下面问题:
(1)若x满足,求的值;
(2)已知正方形的边长为x,E,F分别是上的点,且,长方形的面积是48,分别作正方形和正方形,求阴影部分的面积.
19.(2024七下·太湖期末)已知ABCD,点E在AB与CD之间.
(1)图1中,试说明:∠BED=∠ABE+∠CDE;
(2)图2中,∠ABE的平分线与∠CDE的平分线相交于点F,请利用(1)的结论说明:∠BED=2∠BFD.
(3)图3中,∠ABE的平分线与∠CDE的平分线相交于点F,请直接写出∠BED与∠BFD之间的数量关系.
20.(2024七下·霍邱期末)梅雨季节即将来临,某防汛指挥部在某水域一危险地带的两岸各安置了一盏探照灯,便于夜间察看河水及两岸河堤的情况,如图1,探照灯A射出的光束自顺时针旋转至便立即回转,探照灯B射出的光束自顺时针旋转至便立即回转,两灯不停交叉照射巡视.若探照灯A射出的光束的转动速度是/秒,探照灯B射出的光束的转动速度是/秒,且,满足,假定这一带水域两岸河堤是平行的,即,且.
(1)求,的值.
(2)如图2,两探照灯同时转动,在探照灯A射出的光束首次到达之前,两探照灯射出的光束交于点C.
①过点C作,请写出与的位置关系:________,依据:________________
②若,求的度数.
(3)若探照灯B射出的光束先转动40秒,探照灯A射出的光束才开始转动,在探照灯B射出的光束第一次到达之前,当两探照灯的光束互相平行时,请直接写出探照灯A转动的时间:________.
21.(2024七下·霍邱期末)现有如图1的8张大小形状相同的直角三角形纸片,三边长分别是.用其中4张纸片拼成如图2的大正方形(空白部分是边长分别为和的正方形);用另外4张纸片拼成如图3的大正方形(中间的空白部分是边长为的正方形).
(1)观察:从整体看,图2和图3的大正方形的边长都为,所以图2和图3的大正方形的面积都可以表示为,记为结论①.由于整个图形的面积等于各部分面积的和,所以图2中的大正方形的面积又可以用含字母a、b的代数式表示为: ________,记为结论②;
同样,图3中的大正方形的面积又可以用含字母a、b、c的代数式表示为:________,记为结论③.
(2)思考:
由结论①和结论②,可以得到等式________________
由结论②和结论③,可以得到等式________________
(3)应用:若分别以直角三角形三边为直径,向外作半圆(如图4),三个半圆的面积分别记作、、,且,求的值.
22.(2024七下·宁国期末)某水果商两次去批发市场采购同一种水果,第一次用2000元购进了若干千克,很快卖完,第二次用3000元所购数量比第一次多100千克,且每千克的进价比第一次提高了20%.
(1)求第一次购买水果的进价;
(2)求第二次购买水果的数量:
(3)该水果商按以下方案卖出第二批的水果:先以元/千克的价格售出千克,再以8元/千克的价格售出剩余的全部水果,共获利1600元.若,均为整数,且不超过第二次进价的2倍,求和的值.
23.(2024七下·民勤期末)已知的立方根是2,的算术平方根是4,c是的整数部分.
(1)求a,b,c的值;
(2)求的平方根.
24.(2023七下·迎江期末)阅读下面的文字,解答问题:
大家知道是无理数,而无理数是无限不循环小数,的小数部分我们不可能全部地写出来,于是小明用来表示的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:
∵,即,
∴的整数部分为2,小数部分为.
请解答:
(1)的整数部分是 ,小数部分是 .
(2)如果的小数部分为a,的整数部分为b,求的值;
(3)已知:,其中x是整数,,求的相反数.
25.(2022七下·宜春期末)阅读下面的材料:
对于实数,我们定义符号的意义为:当时,;当时,,如:.
根据上面的材料回答下列问题:
(1)______;
(2)当时,求x的取值范围.
26.(2023七下·怀远期末)某学校2021年在某商场购买甲、乙两种不同的足球,购买甲种足球共花费4000元,购买乙种足球共花费2800元,购买甲种足球数量是购买乙种足球数量的2倍.且购买一个乙种足球比购买一个甲种足球多花20元;
(1)求购买一个甲种足球、一个乙种足球各需多少元;
(2)2022年这所学校决定再次购买甲、乙两种足球共50个.恰逢该商场对两种足球的售价进行调整,甲种足球售价比第一次购买时提高了10%,乙种足球售价比第一次购买时降低了10%.如果此次购买甲、乙两种足球的总费用不超过2910元,那么这所学校最多可购买多少个乙种足球?
27.(2023七下·瑶海期末)中国是最早发现并利用茶的国家,形成了具有独特魅力的茶文化2020年5月21日以“茶和世界共品共享”为主题的第一届国际茶日在中国召开.某茶店用4000元购进了A种茶叶若干盒,用8400元购进B种茶叶若干盒,所购B种茶叶比A种茶叶多10盒,且B种茶叶每盒进价是A种茶叶每盒进价的1.4倍.
(1)A,B两种茶叶每盒进价分别为多少元?
(2)第一次所购茶叶全部售完后第二次购进A,B两种茶叶共100盒(进价不变),A种茶叶的售价是每盒300元,B种茶叶的售价是每盒400元.两种茶叶各售出一半后,为庆祝国际茶日,两种茶叶均打七折销售,全部售出后,第二次所购茶叶的利润为5800元(不考虑其他因素),求本次购进A,B两种茶叶各多少盒?
28.(2023七下·迎江期末)已知关于x的方程
(1)当时,求方程的解;
(2)当m取何值时,此方程无解;
(3)当此方程的解是正数时,求m的取值范围.
答案解析部分
1.(1)解:原式
;
(2)解:原式
(3)解:∵,
∴或或或
因此整数p的值可能为5或或1或.
(1)直接根据"十字相乘法"分解因式,即可得出结果;
(2)先提公因式x,再用十字相乘法进行因式分解,即可得出结果;
(3)先把常数项-6分解成两个因数的积,写出所有可能的结果,然后把两个因数相加,就可得出p所有可能的值。
2.(1)7
(2)7
(3)4
3.(1)A,B两种客房的单价分别是元,元
(2)有3种方案,分别为:
方案1:租住客房间,则租住客房间;
方案2:租住客房间,则租住客房间;
方案3:租住客房间,则租住客房间
4.(1)甲商品的单价为20元;(2)此次最多购进乙商品32件
5.();();.
6.(1)(2)(3)
7.(1)
(2)4
(3)120
8.(1)
(2)
9.(1)
(2)
10.(1)14,
(2).
11.(1)90°
(2)30°
12..
13.(1)
(2)
(3)3、29、55、185
14.(1),
(2)
15.(1)
(2)(ⅰ)(ⅱ)或或
16.(1)平方米
(2)平方米
17.(1),;
(2)10,.
18.(1)11;(2)28.
19.(1)∠BED=∠ABE+∠CDE
(2)∠BED=2∠BFD
(3)∠BED=360°-2∠BFD
20.(1)
(2)①平行,如果两条直线和第三条直线平行,那么这两条直线平行;②
(3)秒或秒
21.(1),
(2),
(3)
22.(1)第一次购买水果的进价为5元/千克
(2)第二次购买水果的数量为500千克
(3)当a的值为12时,m的值为150;当a的值为11时,m的值为200;当a的值为10时,m的值为300
23.(1),,
(2)
24.(1)4,
(2)
(3)
25.(1)﹣1 ;(2)x≥
26.(1)一个甲种足球需50元,一个乙种足球需70元;
(2)这所学校最多可购买20个乙种足球
27.(1)A,B两种茶叶每盒进价分别为200元,280元;(2)第二次购进A种茶叶40盒,B种茶叶60盒
28.(1);
(2);
(3)且
同课章节目录
