数学:2.2《事件的相互独立性》课件(苏教版选修2-3)
文档属性
| 名称 | 数学:2.2《事件的相互独立性》课件(苏教版选修2-3) |

|
|
| 格式 | rar | ||
| 文件大小 | 145.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-15 00:00:00 | ||
图片预览





文档简介
课件12张PPT。事件的相互独立性(2)
习题课复习回顾1、事件的相互独立性设A,B为两个事件,如果 P(AB)=P(A)P(B),则称事件A与事件B相互独立。2、相互独立事件同时发生的概率公式:一般地,如果事件A1,A2……,An相互独立,那么这n个
事件同时发生的概率等于每个事件发生的概率的积,即P(A1·A2……An)=P(A1)·P(A2)……P(An)两个相互独立事件A,B同时发生,即事件A?B发生的概
率为:P(AB)= .P(A)P(B)3、如果事件A、B互斥,那么事件A+B发生(即A,B中有一个发生)的概率:P(A+B)= .P(A)+P(B)一般地,如果事件 ,彼此互斥,那么事件 发生(即 中恰有一个发生)的概率:注:1)求积事件的概率必须注意事件的独立性,事件和的概率必须注意事件是否互斥。
2)明确事件中的关键词,如,“至少有一个发生”“至多有一个发生”,“恰有一个发生”,“都发生”“都不发生”,“不都发生”。课前练习 1、在一段时间内,甲地下雨的概率是0.2,
乙地下雨的概率是0.3,假定在这段时间内
两地是否下雨相互之间没有影响,计算在
这段时间内:
(1)甲、乙两地都下雨的概率; (2)甲、乙两地都不下雨的概率; (3)其中至少有一方下雨的概率.0.060.560.442.某战士射击中靶的概率为0.99.
若连续射击两次.求:
(1) 两次都中靶的概率;
(2)至少有一次中靶的概率:
(3)至多有一次中靶的概率;
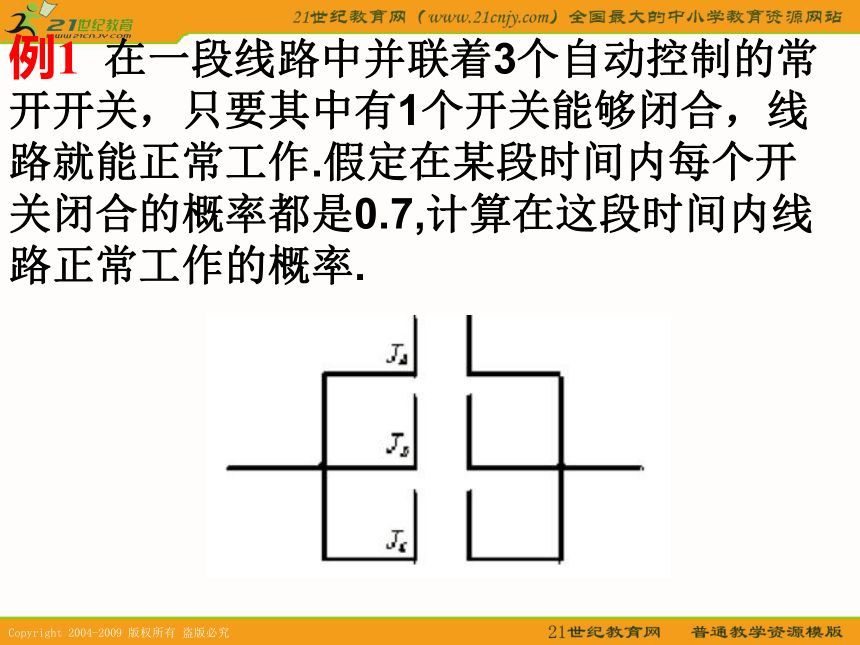
(4)目标被击中的概率.0.98010.99990.01990.9999例1 在一段线路中并联着3个自动控制的常开开关,只要其中有1个开关能够闭合,线路就能正常工作.假定在某段时间内每个开关闭合的概率都是0.7,计算在这段时间内线路正常工作的概率. 由题意,这段时间内3个开关是否能够闭合相
互之间没有影响。所以这段事件内线路正常工作的概率是答:在这段时间内线路正常工作的概率是0.973解:分别记这段时间内开关 能够闭合为事件A,B,C. 根据相互独立事件的概率乘法式这段时间内3个开关都不能闭合的概率是 1.射击时, 甲射10次可射中8次;乙射10
次可射中7次.则甲,乙同时射中同一目标
的概率为_______2.甲袋中有5球 (3红,2白), 乙袋中
有3球(2红,1白).从每袋中任取1球,
则至少取到1个白球的概率是___练习3.甲,乙二人单独解一道题, 若甲,乙
能解对该题的概率分别是m, n .
则此题被解对的概率是_______m+n- mn4.有一谜语, 甲,乙,丙猜对的概率
分别是1/5, 1/3 , 1/4 . 则三人中
恰有一人猜对该谜语的概率是_____练习5.加工某产品须经两道工序, 这两道工序的次品率分别为a, b. 且这两道工序互相独立.产品的合格的概率是 (1-a)(1-b)6.某系统由A,B,C三个元件组成,
每个元件正常工作概率为P.
则系统正常工作的概率为____P+P2- P37.在100件产品中有4件次品.
①从中抽2件, 则2件都是次品概率为___
②从中抽两次,每次1件则两次都抽出次品的概率是___
(不放回抽取)
③从中抽两次,每次1件则两次都抽出次品的概率是_ ___
(放回抽取)求较复杂事件概率正向反向对立事件的概率分类分步P(A+B)= P(A) + P (B)P(A·B)= P(A) · P (B)( 互斥事件)( 互独事件)独立事件不一定互斥.
互斥事件一定不独立.
习题课复习回顾1、事件的相互独立性设A,B为两个事件,如果 P(AB)=P(A)P(B),则称事件A与事件B相互独立。2、相互独立事件同时发生的概率公式:一般地,如果事件A1,A2……,An相互独立,那么这n个
事件同时发生的概率等于每个事件发生的概率的积,即P(A1·A2……An)=P(A1)·P(A2)……P(An)两个相互独立事件A,B同时发生,即事件A?B发生的概
率为:P(AB)= .P(A)P(B)3、如果事件A、B互斥,那么事件A+B发生(即A,B中有一个发生)的概率:P(A+B)= .P(A)+P(B)一般地,如果事件 ,彼此互斥,那么事件 发生(即 中恰有一个发生)的概率:注:1)求积事件的概率必须注意事件的独立性,事件和的概率必须注意事件是否互斥。
2)明确事件中的关键词,如,“至少有一个发生”“至多有一个发生”,“恰有一个发生”,“都发生”“都不发生”,“不都发生”。课前练习 1、在一段时间内,甲地下雨的概率是0.2,
乙地下雨的概率是0.3,假定在这段时间内
两地是否下雨相互之间没有影响,计算在
这段时间内:
(1)甲、乙两地都下雨的概率; (2)甲、乙两地都不下雨的概率; (3)其中至少有一方下雨的概率.0.060.560.442.某战士射击中靶的概率为0.99.
若连续射击两次.求:
(1) 两次都中靶的概率;
(2)至少有一次中靶的概率:
(3)至多有一次中靶的概率;
(4)目标被击中的概率.0.98010.99990.01990.9999例1 在一段线路中并联着3个自动控制的常开开关,只要其中有1个开关能够闭合,线路就能正常工作.假定在某段时间内每个开关闭合的概率都是0.7,计算在这段时间内线路正常工作的概率. 由题意,这段时间内3个开关是否能够闭合相
互之间没有影响。所以这段事件内线路正常工作的概率是答:在这段时间内线路正常工作的概率是0.973解:分别记这段时间内开关 能够闭合为事件A,B,C. 根据相互独立事件的概率乘法式这段时间内3个开关都不能闭合的概率是 1.射击时, 甲射10次可射中8次;乙射10
次可射中7次.则甲,乙同时射中同一目标
的概率为_______2.甲袋中有5球 (3红,2白), 乙袋中
有3球(2红,1白).从每袋中任取1球,
则至少取到1个白球的概率是___练习3.甲,乙二人单独解一道题, 若甲,乙
能解对该题的概率分别是m, n .
则此题被解对的概率是_______m+n- mn4.有一谜语, 甲,乙,丙猜对的概率
分别是1/5, 1/3 , 1/4 . 则三人中
恰有一人猜对该谜语的概率是_____练习5.加工某产品须经两道工序, 这两道工序的次品率分别为a, b. 且这两道工序互相独立.产品的合格的概率是 (1-a)(1-b)6.某系统由A,B,C三个元件组成,
每个元件正常工作概率为P.
则系统正常工作的概率为____P+P2- P37.在100件产品中有4件次品.
①从中抽2件, 则2件都是次品概率为___
②从中抽两次,每次1件则两次都抽出次品的概率是___
(不放回抽取)
③从中抽两次,每次1件则两次都抽出次品的概率是_ ___
(放回抽取)求较复杂事件概率正向反向对立事件的概率分类分步P(A+B)= P(A) + P (B)P(A·B)= P(A) · P (B)( 互斥事件)( 互独事件)独立事件不一定互斥.
互斥事件一定不独立.
