期末复习(2)一元二次方程考点复习(含答案)初中数学浙教版八年级下册
文档属性
| 名称 | 期末复习(2)一元二次方程考点复习(含答案)初中数学浙教版八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 52.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-26 00:00:00 | ||
图片预览




文档简介
期末复习(2)一元二次方程考点复习
一、考点一 一元二次方程的概念
1.下列方程属于一元二次方程的是( )
A. B.2 C. D.
2.一元二次方程二次项系数、一次项系数、常数项分别为( )
A.6,2,9 B.2,,9 C.2,, D.,6,
3.把方程化成一般形式为 .
二、考点二 一元二次方程的解法
4.一元二次方程配方后可化为( )
A. B. C. D.
5.已知关于的方程与有相同的解,则与之间的等量关系为( )
A. B. C. D.
6.关于x的一元二次方程x2=9的解为 .
7.选择适当的方法解下列方程:
(1)
(2)
8.解下列方程
(1)(配方法);
(2)2x2-7x+6=0(公式法).
9.解方程:
(1)x2+4x-5=0;
(2)下面是小蒋同学解一元二次方程的过程,请仔细阅读并完成相应的任务。
解方程: (3x-1)2=2 (3x-1),
解:方程两边同除以(3x-1),得 3x -1=2……第一步
移项,合并同类项,得3x=3……第二步
系数化为1,得x=1……第三步
任务:
①小蒋的解法从第 ▲ 步开始出现错误;
②请写出此题的正确解题过程.
三、考点三 一元二次方程根的判别式
10.已知关于的一元二次方程有两个不相等的实数根,则的取值范围是 .
11.若关于x的一元二次方程有实数根,则a的取值范围是 .
12.若关于的一元二次方程有两个相等的实数根,则的值为 .
13.已知△ABC的两边AB、AC的长是关于x的一元二次方程x2-2(k-1)x+k2-2k=0的两个实数根,第三边BC的长为10.
(1)求证:无论k为何值,此方程总有两个不相等的实数根;
(2)当k为何值时,△ABC是等腰三角形?并求△ABC的周长;
(3)当k为何值时,△ABC是以BC为斜边的直角三角形?
四、考点四 一元二次方程根与系数的关系(选学)
14.关于x的方程x2+4n(x+1)-8n-1=0的两个实数根分别为x1,x2,且x1-x2=10,则n的值为( )
A.2或3 B.3或-2 C.-3或2 D.-3或-2
15.关于x的方程x2+2(m-1)x+m2-m=0有两个实数根a,β,且α2+β2=12,m的值为( )
A.-1 B.-4 C.-4或1 D.-1或4
16. 已知m,n是方程x2+2x-3=0的两个根,则 .
17. (本题8分) 已知关于x的方程有两个不相等的实数根,.
(1) 求实数m的取值范围.
(2) 若,求实数m的值.
18.对于一元二次方程ax2+bx+c=0(a≠0),如果方程有两个实数根为x1,x2,那么,;一元二次方程的这种根与系数的关系,最早是由法国数学家韦达(1540-1603)发现的,因此,我们把这个关系称为韦达定理,灵活运用这个定理有时可以使解题更为简单,根据上述材料,结合你所学的知识,完成下列问题:(1)材料理解:已知一元二次方程x2-3x-2=0两个实数根分别为m,n,求m2n+mn2的值。小明给出了一部分解题思路:
解:(1)∵一元二次方程x2-3x-2=0的两个实数根分别为m,n
∴m+n=____,
∴mn=____,
∴m2n+mn2=____,请填空;
(1)一元二次方程-x2+mx+1=0的一个根为x=2,则m= ,另一个根为x= ;
(2)关于x的一元二次方程:x2+(2m+1)x+m2-2=0有两个实数根,且这两个实数根的平方和是21,求m的值.
五、考点五 一元二次方程的应用
19.随着科技水平的提高,某种电子产品的价格呈下降趋势,今年的价格恰为两年前的一半.假设该电子产品每年降价的百分率均为,则以下所列方程正确的是( )
A. B. C. D.
20. 某建筑工程队在工地一边靠墙处,用81米长的铁栅栏围成三个相连的长方形仓库,仓库总面积为440平方米.为了方便取物,在各个仓库之间留出了1米宽的缺口作通道,在平行于墙的一边留下一个1米宽的缺口作小门.若设AB=x米,则可列方程( )
A.x(81﹣4x)=440 B.x(78﹣2x)=440
C.x(84﹣2x)=440 D.x(84﹣4x)=440
21.如图所示,某景区内有一块长方形油菜花田地(单位:m),现在其中修建一条观花道(阴影部分)供游人赏花,要求观花道的面积占长方形油菜花田地面积的。设观花道的直角边(如图所示)为x,则可列方程为( )
A.(10+x)(9+x)=30 B.(10+x)(9+x)=60
C.(10-x)(9-x)=30 D.(10-x)(9-x)=60
22.某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是91,则每个支干长出小分支的数量是 .
23.综合实践:设计商品最优定价方案
【素材】某经销商计划销售一款新的枕头,根据试售统计,若枕头的售价定为每个50元时,每月可销售100个:若枕头的售价每降价1元,则销售量增加10个,当进货量不超过200个时,枕头的进价为每个20元,当进货量超过200个时,超过200个的部分进价变为每个18元。假设枕头全部售完(进货量=销售量),设每个枕头降价x元(x为整数),回答下列问题、
【问题】
(1)任务1:枕头的实际售价为 (用含x的代数式表示):枕头的销售量为 (用含x的代数式表示).
(2)任务2:若经销商计划进货不超过200个,能否让每月利润达到3750元?若能,请求出此时枕头的售价,反之,请说明理由,(利润=(售价一进价)×销售量)
(3)任务3:依靠试售数据,若该经销商想让每月利润达到最大值,求此时枕头的售价。
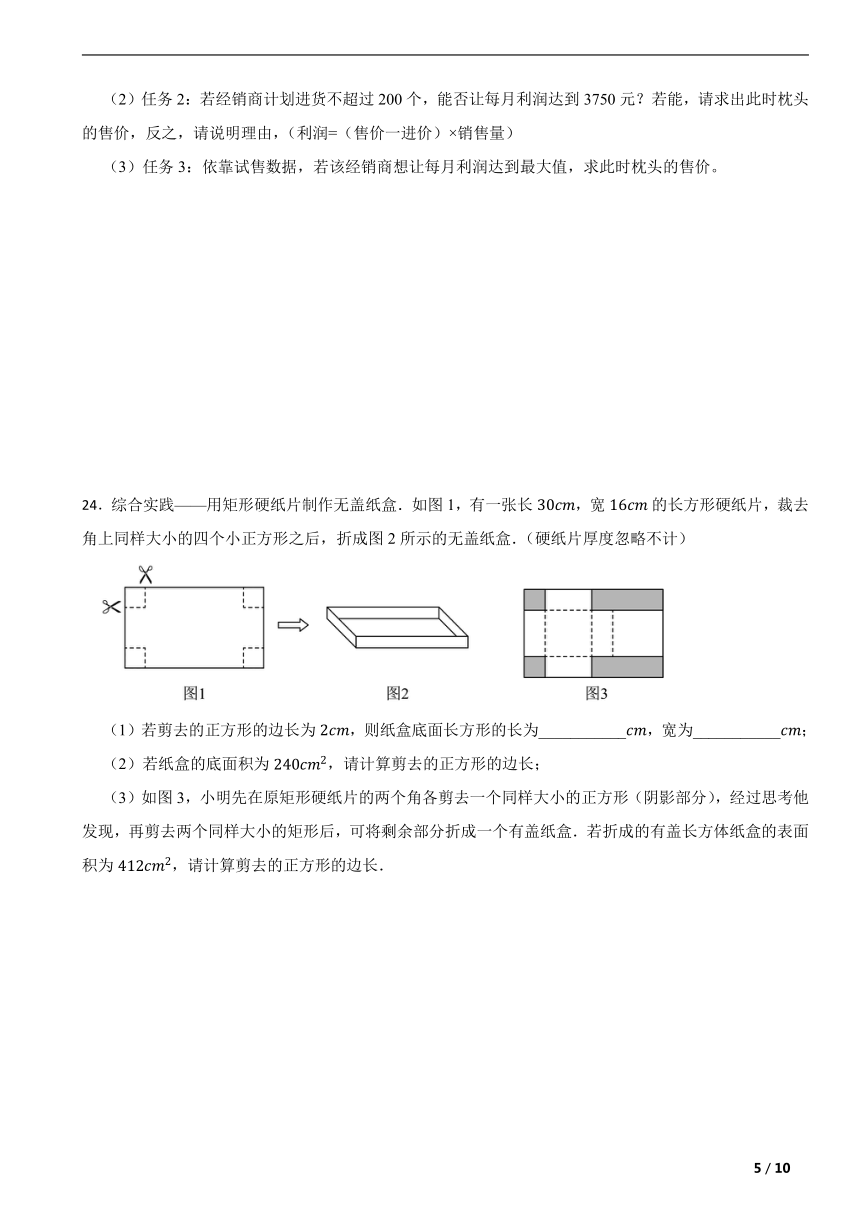
24.综合实践——用矩形硬纸片制作无盖纸盒.如图1,有一张长,宽的长方形硬纸片,裁去角上同样大小的四个小正方形之后,折成图2所示的无盖纸盒.(硬纸片厚度忽略不计)
(1)若剪去的正方形的边长为,则纸盒底面长方形的长为___________,宽为___________;
(2)若纸盒的底面积为,请计算剪去的正方形的边长;
(3)如图3,小明先在原矩形硬纸片的两个角各剪去一个同样大小的正方形(阴影部分),经过思考他发现,再剪去两个同样大小的矩形后,可将剩余部分折成一个有盖纸盒.若折成的有盖长方体纸盒的表面积为,请计算剪去的正方形的边长.
参考答案
1.C
2.C
解:整理得
二次项系数、一次项系数、常数项分别为2,,;
3.
4.B
解:∵,
∴,
5.D
解:∵,
∴,
∴x-1=0或x-m=0,
∴x1=1,x2=m;
∵ ,
∴,
∴,
∴x1=,x2=,
∵两个方程的解相同,
∴,
整理得m-2n=-1.
6.x1=3; x2=-3
解:∵x2=9,
∴x=
∴x=±3,
∴x1=3,x2=-3.
7.(1)解:或
,
(2)解:
或
,
8.(1)解:x2+2x=3
(x+1)2=4
x+1=,
(2)解:a=2,b=7,c=6,
∵△=49-48=1>0,
,
.
9.(1)解:
(2)解: ① 一
②,,
10.且
11.且
12.4
解:∵关于x的一元二次方程 有两个相等的实数根,
13.(1)证明:b2-4ac=4(k-1)2-4(k2-2k)=4>0
无论k为何值,此方程总有两个不相等的实数根.
(2)解:由(1)知方程总有两个不相等的实数根,则当△ABC是等腰三角形时
x=10必定是方程的一个根
当x=10时,102-20(k-1)+k2-2k=0
解得k=10或12
①当k=10时,方程变为x2-18x+80=0
得x=10或8
△ABC的周长为10+10+8=28
②当k=12时,方程变为x2-22x+120=0
得x=10或12
△ABC的周长为10+10+12=32
(3)解:解一元二次方程x2-2(k-1)x+k2-2k=0
x=,x1=k,x2=k-2
∵△ABC是以BC为斜边的直角三角形
∴k2+(k-2)2=102
解得k=8或-6
当k=-6时,AB,AC即x1,x2<0(舍去)
∴k=8时,△ABC是以BC为斜边的直角三角形
14.C
解:∵ x2+4n(x+1)-8n-1=0
∴x2-4nx-4n-1=0,
∵ 关于x的方程x2+4n(x+1)-8n-1=0的两个实数根分别为x1,x2,
∴x1+x2=4n,x1×x2=-4n-1,
∴(x1-x2)2=(x1+x2)2-4x1x2=(4n)2-4(-4n-1)=16n2+16n+4,
又∵ x1-x2=10,
∴16n2+16n+4=100,
∴4n2+4n+1=25,
∴(2n+1)2=25,
∴2n+1=±5,
∴n1=2,n2=-3.
当n=2时,△=(4×2)2-4×(-4×2-1)=100>0,
当n=-3时,△=(-3×4)2-4×[-4×(-3)-1]=100>0,
∴n=2或n=-3都满足题意.
15.A
解:∵关于x的方程 有两个实数根α,β,
则,
解得
又∵, ,
∴
即
则 或 (舍去)。
16.
解:由题意,∵m,n是方程x2+2x-3=0的两个根,
∴m+n=-2,mn=-3
∴
17.(1)解:由题意,得,
解得,
即实数m的取值范围是
(2)解:由根与系数的关系,得,
即,
解得,
由根与系数的关系,得.
在的范围内,
18.(1);
(2)解:设方程的两个根为,
,
,解得,
方程有两个实数根,
,
,
.
19.C
解:假设该电子产品每年降价的百分率均为x,由题意可得.
20.D
解:设仓库的宽为x米 米),则仓库的长为 米,
根据题意得:
21.D
解: 设观花道的直角边为xm,
根据题意得:,
∴(9-x)(10-x)=60.
22.9
23.(1)50-×;100+10x
(2)解:根据题意,得(50-x-20)(100+10x) =3750,
解得:x1=15,x2=5,
当x=15时,100+10x=250,
∵ 经销商计划进货不超过200个,
∴x1=15不符合题意,舍去,
∴50-5=45(元),
∴此时枕头的售价为45元;
(3)解:当进货量不超过200个时,利润为(50-20-x)(100 +10x) =-10(x-10)2+4000,
∵--10(x-10)2≤0,
∴当x=10 时,此时利润最高,为4000元;
当进货量超过200个,即100 +10x>200时,
∴x>10,
此时利润为(50-x-20) ×200 +(50-×-18)×(100 +10x-200)=-10x2+220x+2800,
∴当x=11时,利润最高,即-10(x-11)2+4010=4010,
∴此时枕头售价为50-11=39(元),
∴每月利润最大值时枕头售价为39元,利润为4010元.
24.(1)26,12
(2)解:设减去的正方形的边长为,则纸盒底面长方形的长为,宽为,由题意得:,
解得:或(舍去),
∴剪去正方形的边长为;
(3)解:设剪去的正方形的边长为,由题意得:,
解得:或(不符合题意,舍去),
∴剪去的正方形的边长为.
1 / 1
一、考点一 一元二次方程的概念
1.下列方程属于一元二次方程的是( )
A. B.2 C. D.
2.一元二次方程二次项系数、一次项系数、常数项分别为( )
A.6,2,9 B.2,,9 C.2,, D.,6,
3.把方程化成一般形式为 .
二、考点二 一元二次方程的解法
4.一元二次方程配方后可化为( )
A. B. C. D.
5.已知关于的方程与有相同的解,则与之间的等量关系为( )
A. B. C. D.
6.关于x的一元二次方程x2=9的解为 .
7.选择适当的方法解下列方程:
(1)
(2)
8.解下列方程
(1)(配方法);
(2)2x2-7x+6=0(公式法).
9.解方程:
(1)x2+4x-5=0;
(2)下面是小蒋同学解一元二次方程的过程,请仔细阅读并完成相应的任务。
解方程: (3x-1)2=2 (3x-1),
解:方程两边同除以(3x-1),得 3x -1=2……第一步
移项,合并同类项,得3x=3……第二步
系数化为1,得x=1……第三步
任务:
①小蒋的解法从第 ▲ 步开始出现错误;
②请写出此题的正确解题过程.
三、考点三 一元二次方程根的判别式
10.已知关于的一元二次方程有两个不相等的实数根,则的取值范围是 .
11.若关于x的一元二次方程有实数根,则a的取值范围是 .
12.若关于的一元二次方程有两个相等的实数根,则的值为 .
13.已知△ABC的两边AB、AC的长是关于x的一元二次方程x2-2(k-1)x+k2-2k=0的两个实数根,第三边BC的长为10.
(1)求证:无论k为何值,此方程总有两个不相等的实数根;
(2)当k为何值时,△ABC是等腰三角形?并求△ABC的周长;
(3)当k为何值时,△ABC是以BC为斜边的直角三角形?
四、考点四 一元二次方程根与系数的关系(选学)
14.关于x的方程x2+4n(x+1)-8n-1=0的两个实数根分别为x1,x2,且x1-x2=10,则n的值为( )
A.2或3 B.3或-2 C.-3或2 D.-3或-2
15.关于x的方程x2+2(m-1)x+m2-m=0有两个实数根a,β,且α2+β2=12,m的值为( )
A.-1 B.-4 C.-4或1 D.-1或4
16. 已知m,n是方程x2+2x-3=0的两个根,则 .
17. (本题8分) 已知关于x的方程有两个不相等的实数根,.
(1) 求实数m的取值范围.
(2) 若,求实数m的值.
18.对于一元二次方程ax2+bx+c=0(a≠0),如果方程有两个实数根为x1,x2,那么,;一元二次方程的这种根与系数的关系,最早是由法国数学家韦达(1540-1603)发现的,因此,我们把这个关系称为韦达定理,灵活运用这个定理有时可以使解题更为简单,根据上述材料,结合你所学的知识,完成下列问题:(1)材料理解:已知一元二次方程x2-3x-2=0两个实数根分别为m,n,求m2n+mn2的值。小明给出了一部分解题思路:
解:(1)∵一元二次方程x2-3x-2=0的两个实数根分别为m,n
∴m+n=____,
∴mn=____,
∴m2n+mn2=____,请填空;
(1)一元二次方程-x2+mx+1=0的一个根为x=2,则m= ,另一个根为x= ;
(2)关于x的一元二次方程:x2+(2m+1)x+m2-2=0有两个实数根,且这两个实数根的平方和是21,求m的值.
五、考点五 一元二次方程的应用
19.随着科技水平的提高,某种电子产品的价格呈下降趋势,今年的价格恰为两年前的一半.假设该电子产品每年降价的百分率均为,则以下所列方程正确的是( )
A. B. C. D.
20. 某建筑工程队在工地一边靠墙处,用81米长的铁栅栏围成三个相连的长方形仓库,仓库总面积为440平方米.为了方便取物,在各个仓库之间留出了1米宽的缺口作通道,在平行于墙的一边留下一个1米宽的缺口作小门.若设AB=x米,则可列方程( )
A.x(81﹣4x)=440 B.x(78﹣2x)=440
C.x(84﹣2x)=440 D.x(84﹣4x)=440
21.如图所示,某景区内有一块长方形油菜花田地(单位:m),现在其中修建一条观花道(阴影部分)供游人赏花,要求观花道的面积占长方形油菜花田地面积的。设观花道的直角边(如图所示)为x,则可列方程为( )
A.(10+x)(9+x)=30 B.(10+x)(9+x)=60
C.(10-x)(9-x)=30 D.(10-x)(9-x)=60
22.某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干、支干和小分支的总数是91,则每个支干长出小分支的数量是 .
23.综合实践:设计商品最优定价方案
【素材】某经销商计划销售一款新的枕头,根据试售统计,若枕头的售价定为每个50元时,每月可销售100个:若枕头的售价每降价1元,则销售量增加10个,当进货量不超过200个时,枕头的进价为每个20元,当进货量超过200个时,超过200个的部分进价变为每个18元。假设枕头全部售完(进货量=销售量),设每个枕头降价x元(x为整数),回答下列问题、
【问题】
(1)任务1:枕头的实际售价为 (用含x的代数式表示):枕头的销售量为 (用含x的代数式表示).
(2)任务2:若经销商计划进货不超过200个,能否让每月利润达到3750元?若能,请求出此时枕头的售价,反之,请说明理由,(利润=(售价一进价)×销售量)
(3)任务3:依靠试售数据,若该经销商想让每月利润达到最大值,求此时枕头的售价。
24.综合实践——用矩形硬纸片制作无盖纸盒.如图1,有一张长,宽的长方形硬纸片,裁去角上同样大小的四个小正方形之后,折成图2所示的无盖纸盒.(硬纸片厚度忽略不计)
(1)若剪去的正方形的边长为,则纸盒底面长方形的长为___________,宽为___________;
(2)若纸盒的底面积为,请计算剪去的正方形的边长;
(3)如图3,小明先在原矩形硬纸片的两个角各剪去一个同样大小的正方形(阴影部分),经过思考他发现,再剪去两个同样大小的矩形后,可将剩余部分折成一个有盖纸盒.若折成的有盖长方体纸盒的表面积为,请计算剪去的正方形的边长.
参考答案
1.C
2.C
解:整理得
二次项系数、一次项系数、常数项分别为2,,;
3.
4.B
解:∵,
∴,
5.D
解:∵,
∴,
∴x-1=0或x-m=0,
∴x1=1,x2=m;
∵ ,
∴,
∴,
∴x1=,x2=,
∵两个方程的解相同,
∴,
整理得m-2n=-1.
6.x1=3; x2=-3
解:∵x2=9,
∴x=
∴x=±3,
∴x1=3,x2=-3.
7.(1)解:或
,
(2)解:
或
,
8.(1)解:x2+2x=3
(x+1)2=4
x+1=,
(2)解:a=2,b=7,c=6,
∵△=49-48=1>0,
,
.
9.(1)解:
(2)解: ① 一
②,,
10.且
11.且
12.4
解:∵关于x的一元二次方程 有两个相等的实数根,
13.(1)证明:b2-4ac=4(k-1)2-4(k2-2k)=4>0
无论k为何值,此方程总有两个不相等的实数根.
(2)解:由(1)知方程总有两个不相等的实数根,则当△ABC是等腰三角形时
x=10必定是方程的一个根
当x=10时,102-20(k-1)+k2-2k=0
解得k=10或12
①当k=10时,方程变为x2-18x+80=0
得x=10或8
△ABC的周长为10+10+8=28
②当k=12时,方程变为x2-22x+120=0
得x=10或12
△ABC的周长为10+10+12=32
(3)解:解一元二次方程x2-2(k-1)x+k2-2k=0
x=,x1=k,x2=k-2
∵△ABC是以BC为斜边的直角三角形
∴k2+(k-2)2=102
解得k=8或-6
当k=-6时,AB,AC即x1,x2<0(舍去)
∴k=8时,△ABC是以BC为斜边的直角三角形
14.C
解:∵ x2+4n(x+1)-8n-1=0
∴x2-4nx-4n-1=0,
∵ 关于x的方程x2+4n(x+1)-8n-1=0的两个实数根分别为x1,x2,
∴x1+x2=4n,x1×x2=-4n-1,
∴(x1-x2)2=(x1+x2)2-4x1x2=(4n)2-4(-4n-1)=16n2+16n+4,
又∵ x1-x2=10,
∴16n2+16n+4=100,
∴4n2+4n+1=25,
∴(2n+1)2=25,
∴2n+1=±5,
∴n1=2,n2=-3.
当n=2时,△=(4×2)2-4×(-4×2-1)=100>0,
当n=-3时,△=(-3×4)2-4×[-4×(-3)-1]=100>0,
∴n=2或n=-3都满足题意.
15.A
解:∵关于x的方程 有两个实数根α,β,
则,
解得
又∵, ,
∴
即
则 或 (舍去)。
16.
解:由题意,∵m,n是方程x2+2x-3=0的两个根,
∴m+n=-2,mn=-3
∴
17.(1)解:由题意,得,
解得,
即实数m的取值范围是
(2)解:由根与系数的关系,得,
即,
解得,
由根与系数的关系,得.
在的范围内,
18.(1);
(2)解:设方程的两个根为,
,
,解得,
方程有两个实数根,
,
,
.
19.C
解:假设该电子产品每年降价的百分率均为x,由题意可得.
20.D
解:设仓库的宽为x米 米),则仓库的长为 米,
根据题意得:
21.D
解: 设观花道的直角边为xm,
根据题意得:,
∴(9-x)(10-x)=60.
22.9
23.(1)50-×;100+10x
(2)解:根据题意,得(50-x-20)(100+10x) =3750,
解得:x1=15,x2=5,
当x=15时,100+10x=250,
∵ 经销商计划进货不超过200个,
∴x1=15不符合题意,舍去,
∴50-5=45(元),
∴此时枕头的售价为45元;
(3)解:当进货量不超过200个时,利润为(50-20-x)(100 +10x) =-10(x-10)2+4000,
∵--10(x-10)2≤0,
∴当x=10 时,此时利润最高,为4000元;
当进货量超过200个,即100 +10x>200时,
∴x>10,
此时利润为(50-x-20) ×200 +(50-×-18)×(100 +10x-200)=-10x2+220x+2800,
∴当x=11时,利润最高,即-10(x-11)2+4010=4010,
∴此时枕头售价为50-11=39(元),
∴每月利润最大值时枕头售价为39元,利润为4010元.
24.(1)26,12
(2)解:设减去的正方形的边长为,则纸盒底面长方形的长为,宽为,由题意得:,
解得:或(舍去),
∴剪去正方形的边长为;
(3)解:设剪去的正方形的边长为,由题意得:,
解得:或(不符合题意,舍去),
∴剪去的正方形的边长为.
1 / 1
同课章节目录
