华东师大版2024—2025学年八年级下册数学期末考试模拟试卷(含答案)
文档属性
| 名称 | 华东师大版2024—2025学年八年级下册数学期末考试模拟试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 861.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-25 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
华东师大版2024—2025学年八年级下册数学期末考试模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.将0.000000843米用科学记数法表示为( )
A.8.43×10﹣6 B.8.43×10﹣7 C.8.43×106 D.8.43×107
2.直线y=﹣3x+2经过的象限为( )
A.第一、二、四象限 B.第一、二、三象限
C.第一、三、四象限 D.第二、三、四象限
3.下列图象中,表示y是x的函数的是( )
A.B. C.D.
4.若点A(2,﹣3),B(4,3),(5,a)在同一条直线上,则a的值是( )
A.6或﹣6 B.6 C.﹣6 D.6或3
5.某校举办水浒文化进校园朗诵大赛,比赛中七位评委给某位参赛选手的分数,如果去掉一个最高分和一个最低分,则下列数据一定不发生变化的是( )
A.中位数 B.众数 C.平均数 D.方差
6.已知平行四边形ABCD中,∠A+∠C=130°,则∠D的度数是( )
A.50° B.65° C.115° D.130°
7.若把分式中的x和y都扩大2倍,那么分式的值( )
A.扩大2倍 B.不变 C.缩小2倍 D.缩小4倍
8.关于x的函数y=k(x﹣2)和y(k≠0),它们在同一坐标系内的图象大致是( )
A.B. C.D.
9.下列平行四边形中,根据图中所标出的数据,不能判定是菱形的是( )
A. B. C. D.
10.出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一,如图,在矩形ABCD中,AB=5,AD=12,对角线AC与BD交于点O,点E为BC边上的一个动点,EF⊥AC,EG⊥BD,垂足分别为点F,G,则EF+EG的值为( )
A. B. C. D.
二、填空题(6小题,每题3分,共18分)
11.要使分式有意义,则x的取值应满足的条件为 .
12.如图,直线y=﹣x+3与y=mx+n交点的横坐标为1,则关于x,y的二元一次方程组的解为 .
13.一次函数y=(2m﹣3)x+3﹣m的图象经过第一、二、三象限,则m的取值范围是 .
14.如图,点A是反比例函数y在第四象限上的点,AB⊥x轴,若S△AOB=1,则k的值为 .
15.如图,平行四边形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点F、E,若设该平行四边形的面积为16,则图中阴影部分的面积为 .
16.如图,在平面直角坐标系xOy中,点A、B分别在函数y(x>0)和y(x<0)的图象上,AB∥x轴,点C是y轴上一点,线段AC与x轴的正半轴交于点D,若△ABC的面积为18,,则k的值为 .
第II卷
华东师大版2024—2025学年八年级下册数学期末考试模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再取一个合适的数作为x的值代入求值.
18.解下列分式方程
(1)(2)
19.某校八年级1,2班开展了一次禁毒知识竞赛,每班选25名同学参赛,成绩评为A,B,C,D四个等级,相应等级的得分依次为100分,90分,80分,70分,将两个班的成绩整理后,绘制成如所示统计图表:
平均数 中位数 众数
1班 a b 90
2班 87.6 80 c
(1)请把1班竞赛成绩统计图补充完整.
(2)计算出表格中a,b,c的值:a= ,b= ,c= .
(3)请你根据平均数和众数,分析比较1班和2班的竞赛成绩.
20.如图,在 ABCD中,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F,交BE于点G.
(1)求证:AF=DE.
(2)若AD=16,EF=12,请求出 ABCD的周长.
21.如图,在矩形ABCD中,AC,BD相交于点O,AE∥BD,BE∥AC.
(1)求证:四边形AEBO是菱形;
(2)若AB=2,OB=3,求AD的长及四边形AEBO的面积.
22.某商店用3000元购进一批小学生书包,出售后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了2元,结果购买第二批书包用了9900元.
(1)请求出第一批每只书包的进价;
(2)该商店第一批和第二批分别购进了多少只书包;
(3)若商店销售这两批书包时,每个售价都是30元,全部售出后,商店共盈利多少元?
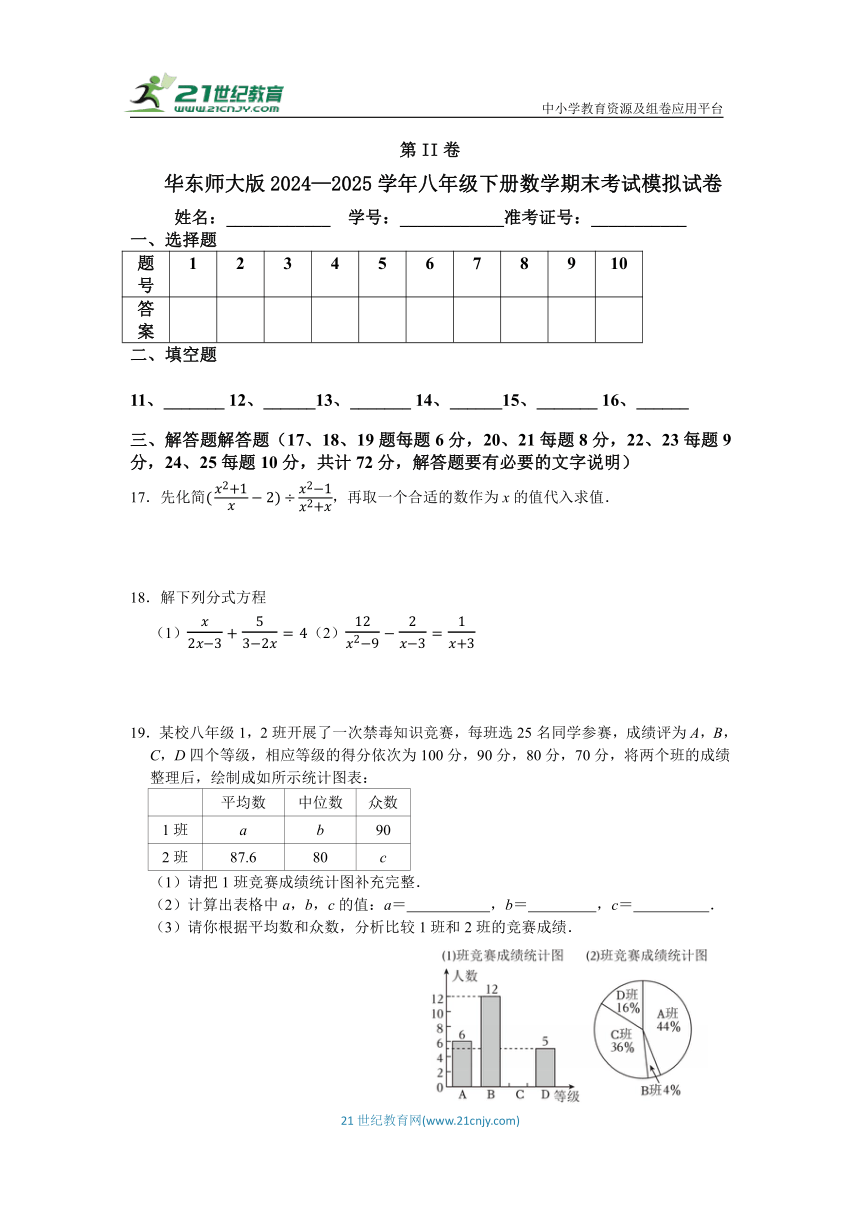
23.如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数的图象交于A(1,m),B(n,1)两点,与y轴交于点M,与x轴交于点N.
(1)求直线AB的解析式;
(2)当时,x的取值范围为 ;
(3)如图,y轴正半轴上有一点P,OP=2,连接AP,OB,求四边形OPAB的面积.
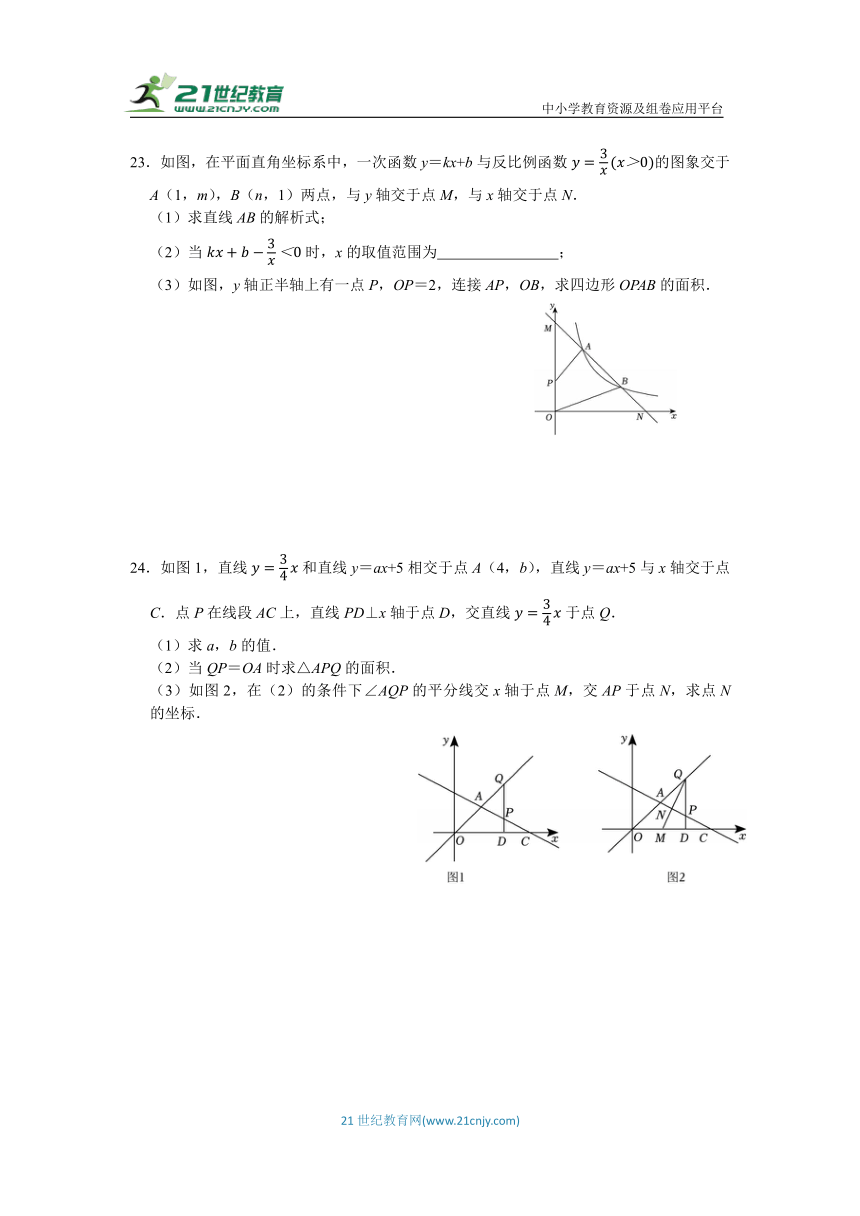
24.如图1,直线和直线y=ax+5相交于点A(4,b),直线y=ax+5与x轴交于点C.点P在线段AC上,直线PD⊥x轴于点D,交直线于点Q.
(1)求a,b的值.
(2)当QP=OA时求△APQ的面积.
(3)如图2,在(2)的条件下∠AQP的平分线交x轴于点M,交AP于点N,求点N的坐标.
25.如图1,在正方形ABCD中,E是边BC上的一点,在AE的右上方作正方形AEFG,连接DG.
(1)求证:∠ADG=90°;
(2)如图2,连接BG、BD、BF、DF,记△ABG、△BDF的面积分别为S1,S2,求的值;
(3)如图3,当点E在边BC的延长线上时,连接AF,交线段DG于点M,当CE=3DM时,试判断CG与DM的数量关系,并加以证明.
参考答案
选择题
1—10:BCDBA CCCCC
二、填空题
11.【解答】解:由题意可得:x+1≠0,
解得x≠﹣1,
故答案为:x≠﹣1.
12.【解答】解:∵直线y=﹣x+3与y=mx+n交点的横坐标为1,
∴纵坐标为y=﹣1+3=2,
∴两直线交点坐标(1,2),
∴x,y的方程组的解为,
故答案为:.
13.【解答】解:∵函数y=(2m﹣3)x+3﹣m的图象经过第一、二、三象限,
∴,
∴1.5<m<3.
故答案为:1.5<m<3.
14.【解答】解:设A(x,y),
则OB=x,AB=﹣y,
∵S△AOB=1,
∴OB×AB=1,
∴﹣xy=2,
∴xy=﹣2,
∵点A在y上,
∴k=xy=﹣2,
故答案为:﹣2.
15.【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,OA=OC,OB=OD,AD∥BC,
∴∠FAO=∠ECO,∠FDO=∠EBO,
在△AOB和△COD中,
,
∴△AOB≌△COD(SSS),
∴S△AOB=S△COD,
在△AFO和△CEO中,
,
∴△AFO≌△CEO(ASA),
同理,△BOE≌△DOF(ASA),
∴S△AFO=S△CEO,S△BOE=S△DOF,
∴阴影部分的面积=S四边形ABEFS平行四边形ABCD16=8.
故答案为:8.
16.【解答】解:如图,设AB与y轴交于点E,过点A、点B分别作AM⊥x轴,BN⊥x轴,垂足分别为M、N,
∵点A、点B分别在两个反比例函数的图象上,
∴反比例函数系数k的几何意义可知,S矩形AEOM=14,S矩形OEBN=|k|=﹣k,
∵△ABC的面积为18,,
∴,
∴S△ADB=12,
∵,
∴S矩形ABNM=2S△ADB=24,
∴S矩形OEBN=24﹣14=10=﹣k,
∴k=﹣10,
故答案为:﹣10.
三、解答题
17.【解答】解:原式
,
∵|2x﹣y+1|+(3x﹣2y+4)2=0,|2x﹣y+1|≥0,(3x﹣2y+4)2≥0,
∴2x﹣y+1=0且3x﹣2y+4=0,
解得:x=2,y=5,
当x=2,y=5时,原式.
18.【解答】解:原式
=x﹣1.
∵x不能为0,±1,
∴当x为3时,
原式=3﹣1=2.
19.【解答】解:(1)∵每班选25名同学参加比赛,
∴(1)班C等级的人数是:25﹣6﹣12﹣5=2(人),
补充统计图如图:
(2)a=(6×100+12×90+2×80+5×70)=87.6,
∵(1)班有6人100分,12人90分,2人80分,5人70分,
∴按照从小到大的顺序将成绩排列,正中间的成绩为90分,
∴b=90,
∵由扇形统计图可知:(2)班等级为A的占44%,为最多,
∴(2)班成绩为100分的人数最多,
∴c=100,
(3)②∵(1)班和(2)班的平均成绩均为87.6分,而(1)班的众数是90分,(2)班的众数是100分,
∴从平均数和众数方面进行比较,(2)班成绩更好.
20.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠AEB=∠CBE,
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE∠ABC,
∴∠ABE=∠AEB,
∴AE=AB,
同理可得:DF=CD,
∴AE=DF,
∴AE﹣EF=DF﹣EF,
∴AF=DE;
(2)解:∵AD=16,
∴AF+EF+DE=16,
∵AF=DE,EF=12,
∴AF+12+AF=16,
解得AF=2,
∴AB=AE=AF+EF=2+12=14,
∴ ABCD的周长为2(AB+AD)=2×(16+14)=60,即 ABCD的周长为60.
21.【解答】(1)证明:∵AE∥BD,BE∥AC,
∴四边形AEBO是平行四边形,
∵四边形ABCD是矩形,
∴AO=CO,BO=DO,AC=BD,
∴OA=OB,
∴四边形AEBO是菱形;
(2)解:∵四边形ABCD是矩形,
∴∠DAB=90°,AO=CO,BO=DO,AC=BD,
∴OA=OB=OC=DO,
∵OB=3,
∴BD=6,
由勾股定理得:AD4,
∵BO=DO,
∴S△AOB=S△AODS△BADAD×AB42=2,
∵四边形AEBO是菱形,
∴AE=AO=BO=BE=3,
∴△AEB≌△BOA(SSS),
∴△AEB的面积=△AOB的面积=2,
∴四边形AEBO的面积是22=4.
22.【解答】解:(1)设第一批每只书包的单价为x元,则第二批每只书包的单价为(x+2)元,
根据题意得:3,
解得:x=20,
经检验:x=20是分式方程的解,且符合题意,
答:第一批每只书包的单价为20元;
(2)第一批购进书包的数量=3000÷20=150(只);
第二批购进书包的数量=3×150=450(只),
答:该商店第一批购进了150只书包,第二批购进了450只书包;
(3)30×(150+450)﹣3000﹣9900=5100(元),
答:全部售出后,商店共盈利5100元.
23.【解答】解:(1)把A(1,m),B(n,1)两点坐标分别代入反比例函数,可得,,
∴m=3,n=3,
∴A(1,3),B(3,1).
把A(1,3),B(3,1)代入一次函数y=kx+b,
可得,解得,
∴直线AB的解析式为y=﹣x+4.
(2)由图象可知不等式的解集为:0<x<1或x>3.
(3)如图,过点B作BE⊥y轴于点E,过点A作AF⊥y轴于点F,
∵直线AB的解析式为y=﹣x+4,
∴M点坐标为(0,4),
∴PM=OM﹣OP=4﹣2=2,
∵A(1,3),B(3,1),
∴AF=1,BE=3,
∴四边形OPAB的面积=S△OBM﹣S△PAM
=5.
24.【解答】解:(1)根据已知条件直线和直线y=ax+5相交于点A(4,b),
∴A(4,b )代入yx,
∴b=3,
∴A(4,3),代入y=ax+5,
得a,
∴a,b=3;
(2)∵A(4,3),
∴OA,
∵QP=OA,
∴QP=5,
∵P在yx+5上,
设P(n,n+5),
∵PQ⊥x轴交yx于Q,
∴Q(n,n),
∴,
解得:n=8,
∴Q(8,6)P(8,1),
S△APQ5×4=10;
(3)如图:作ME⊥OQ于点E,
∵MD⊥PD,QM平分∠OQD,
∴ME=MD,
∵Q(8,6),O(0,0),
∴OQ=10,(根据平面直角坐标系中两点间距离公式),
由(2)可知:OD=8,QD=6,
∵S△OQD=S△OMQ+S△ODM,
∴OQ×MEMD×QDOD×QD,
10×MD+MD×6=8×6,
解得:MD=3,
∴OM=OD﹣MD=8﹣3=5,
∴M(5,0),
设直线QM为y=kx+c,
∴,
解得:,
QM为:y=2x﹣10,
∵AP、QM交于N点,
∴,
解得:,
∴N(6,2).
25.【解答】(1)证明:如图1,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠ABC=90°,
即∠BAE+∠EAD=90°,
∵四边形AEFG是正方形,
∴AE=AG,∠EAG=90°,
即∠DAG+∠EAD=90°,
∴∠BAE=∠DAG,
∴△ABE≌△ADG(SAS),
∴∠ADG=∠ABE=90°;
(2)解:由(1)知,∠ADG=90°;
∵四边形ABCD是正方形,
∴AB∥CD,∠ABC=∠ADC=90°,AB=BC,∠DBC=45°,
∴∠ADG+∠ADC=180°,
∴点C、D、G在一条直线上,
∵AB∥CD,
∴,
过点F作FN⊥BC的延长线于点N,连接CF,如图2,
∵∠ABC=90°,
∴∠1+∠2=90°,
∵四边形AEFG是正方形,
∴AE=EF,∠AEF=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
又∵∠ABE=∠ENF=90°,AE=EF,
∴△ABE≌△ENF(AAS),
∴AB=EN,BE=NF,
∵BC=AB,
∴BC=EN,
∴BC﹣CE=EN﹣CE,
即BE=CN,
∴NF=CN,
∴△FCN是等腰直角三角形,
∴∠FCN=45°,
∴∠DBC=∠FCN,
∴CF∥BD,
∴,
∴;
(3)解:CG=9DM,理由:
在BC上截取BH=DM,连接AH,ME,如图3,
∵∠ABH=∠ADM=90°,AB=AD,BH=DM,
∴△ABH≌△ADM(SAS),
∴AH=AM,∠3=∠1,
∵四边形AEFG是正方形,
∴∠EAF=45°,
即∠1+∠2=45°,
∴∠3+∠2=45°,
∴∠HAE=90°﹣45°=45°,
∴∠HAE=∠EAF,
又∵AH=AM,AE=AE,
∴△HAE≌△MAE(SAS),
∴HE=ME,
设DM=b,
∵CE=3DM,
∴CE=3b,
设正方形ABCD的边长为a,
∴BE=BC+CE=a+3b,BH=DM=b,
∴HE=BE﹣BH=a+3b﹣b=a+2b,CM=CD+DM=a+b,
∴ME=HE=a+2b,
∵∠MCE=90°,
∴由勾股定理得ME2=CM2+CE2,
∴(a+2b)2=(a+b)2+(3b)2,
解得a=3b,
∴BE=a+3b=6b,
又由(1)知△ABE≌△ADG,
∴DG=BE=6b,
∴CG=CD+DG=a+6b=3b+6b=9b,
∵DM=b,
∴CG=9DM.
21世纪教育网(www.21cnjy.com)
华东师大版2024—2025学年八年级下册数学期末考试模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.将0.000000843米用科学记数法表示为( )
A.8.43×10﹣6 B.8.43×10﹣7 C.8.43×106 D.8.43×107
2.直线y=﹣3x+2经过的象限为( )
A.第一、二、四象限 B.第一、二、三象限
C.第一、三、四象限 D.第二、三、四象限
3.下列图象中,表示y是x的函数的是( )
A.B. C.D.
4.若点A(2,﹣3),B(4,3),(5,a)在同一条直线上,则a的值是( )
A.6或﹣6 B.6 C.﹣6 D.6或3
5.某校举办水浒文化进校园朗诵大赛,比赛中七位评委给某位参赛选手的分数,如果去掉一个最高分和一个最低分,则下列数据一定不发生变化的是( )
A.中位数 B.众数 C.平均数 D.方差
6.已知平行四边形ABCD中,∠A+∠C=130°,则∠D的度数是( )
A.50° B.65° C.115° D.130°
7.若把分式中的x和y都扩大2倍,那么分式的值( )
A.扩大2倍 B.不变 C.缩小2倍 D.缩小4倍
8.关于x的函数y=k(x﹣2)和y(k≠0),它们在同一坐标系内的图象大致是( )
A.B. C.D.
9.下列平行四边形中,根据图中所标出的数据,不能判定是菱形的是( )
A. B. C. D.
10.出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一,如图,在矩形ABCD中,AB=5,AD=12,对角线AC与BD交于点O,点E为BC边上的一个动点,EF⊥AC,EG⊥BD,垂足分别为点F,G,则EF+EG的值为( )
A. B. C. D.
二、填空题(6小题,每题3分,共18分)
11.要使分式有意义,则x的取值应满足的条件为 .
12.如图,直线y=﹣x+3与y=mx+n交点的横坐标为1,则关于x,y的二元一次方程组的解为 .
13.一次函数y=(2m﹣3)x+3﹣m的图象经过第一、二、三象限,则m的取值范围是 .
14.如图,点A是反比例函数y在第四象限上的点,AB⊥x轴,若S△AOB=1,则k的值为 .
15.如图,平行四边形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD和BC于点F、E,若设该平行四边形的面积为16,则图中阴影部分的面积为 .
16.如图,在平面直角坐标系xOy中,点A、B分别在函数y(x>0)和y(x<0)的图象上,AB∥x轴,点C是y轴上一点,线段AC与x轴的正半轴交于点D,若△ABC的面积为18,,则k的值为 .
第II卷
华东师大版2024—2025学年八年级下册数学期末考试模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再取一个合适的数作为x的值代入求值.
18.解下列分式方程
(1)(2)
19.某校八年级1,2班开展了一次禁毒知识竞赛,每班选25名同学参赛,成绩评为A,B,C,D四个等级,相应等级的得分依次为100分,90分,80分,70分,将两个班的成绩整理后,绘制成如所示统计图表:
平均数 中位数 众数
1班 a b 90
2班 87.6 80 c
(1)请把1班竞赛成绩统计图补充完整.
(2)计算出表格中a,b,c的值:a= ,b= ,c= .
(3)请你根据平均数和众数,分析比较1班和2班的竞赛成绩.
20.如图,在 ABCD中,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F,交BE于点G.
(1)求证:AF=DE.
(2)若AD=16,EF=12,请求出 ABCD的周长.
21.如图,在矩形ABCD中,AC,BD相交于点O,AE∥BD,BE∥AC.
(1)求证:四边形AEBO是菱形;
(2)若AB=2,OB=3,求AD的长及四边形AEBO的面积.
22.某商店用3000元购进一批小学生书包,出售后发现供不应求,商店又购进第二批同样的书包,所购数量是第一批购进数量的3倍,但单价贵了2元,结果购买第二批书包用了9900元.
(1)请求出第一批每只书包的进价;
(2)该商店第一批和第二批分别购进了多少只书包;
(3)若商店销售这两批书包时,每个售价都是30元,全部售出后,商店共盈利多少元?
23.如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数的图象交于A(1,m),B(n,1)两点,与y轴交于点M,与x轴交于点N.
(1)求直线AB的解析式;
(2)当时,x的取值范围为 ;
(3)如图,y轴正半轴上有一点P,OP=2,连接AP,OB,求四边形OPAB的面积.
24.如图1,直线和直线y=ax+5相交于点A(4,b),直线y=ax+5与x轴交于点C.点P在线段AC上,直线PD⊥x轴于点D,交直线于点Q.
(1)求a,b的值.
(2)当QP=OA时求△APQ的面积.
(3)如图2,在(2)的条件下∠AQP的平分线交x轴于点M,交AP于点N,求点N的坐标.
25.如图1,在正方形ABCD中,E是边BC上的一点,在AE的右上方作正方形AEFG,连接DG.
(1)求证:∠ADG=90°;
(2)如图2,连接BG、BD、BF、DF,记△ABG、△BDF的面积分别为S1,S2,求的值;
(3)如图3,当点E在边BC的延长线上时,连接AF,交线段DG于点M,当CE=3DM时,试判断CG与DM的数量关系,并加以证明.
参考答案
选择题
1—10:BCDBA CCCCC
二、填空题
11.【解答】解:由题意可得:x+1≠0,
解得x≠﹣1,
故答案为:x≠﹣1.
12.【解答】解:∵直线y=﹣x+3与y=mx+n交点的横坐标为1,
∴纵坐标为y=﹣1+3=2,
∴两直线交点坐标(1,2),
∴x,y的方程组的解为,
故答案为:.
13.【解答】解:∵函数y=(2m﹣3)x+3﹣m的图象经过第一、二、三象限,
∴,
∴1.5<m<3.
故答案为:1.5<m<3.
14.【解答】解:设A(x,y),
则OB=x,AB=﹣y,
∵S△AOB=1,
∴OB×AB=1,
∴﹣xy=2,
∴xy=﹣2,
∵点A在y上,
∴k=xy=﹣2,
故答案为:﹣2.
15.【解答】解:∵四边形ABCD是平行四边形,
∴AB=CD,OA=OC,OB=OD,AD∥BC,
∴∠FAO=∠ECO,∠FDO=∠EBO,
在△AOB和△COD中,
,
∴△AOB≌△COD(SSS),
∴S△AOB=S△COD,
在△AFO和△CEO中,
,
∴△AFO≌△CEO(ASA),
同理,△BOE≌△DOF(ASA),
∴S△AFO=S△CEO,S△BOE=S△DOF,
∴阴影部分的面积=S四边形ABEFS平行四边形ABCD16=8.
故答案为:8.
16.【解答】解:如图,设AB与y轴交于点E,过点A、点B分别作AM⊥x轴,BN⊥x轴,垂足分别为M、N,
∵点A、点B分别在两个反比例函数的图象上,
∴反比例函数系数k的几何意义可知,S矩形AEOM=14,S矩形OEBN=|k|=﹣k,
∵△ABC的面积为18,,
∴,
∴S△ADB=12,
∵,
∴S矩形ABNM=2S△ADB=24,
∴S矩形OEBN=24﹣14=10=﹣k,
∴k=﹣10,
故答案为:﹣10.
三、解答题
17.【解答】解:原式
,
∵|2x﹣y+1|+(3x﹣2y+4)2=0,|2x﹣y+1|≥0,(3x﹣2y+4)2≥0,
∴2x﹣y+1=0且3x﹣2y+4=0,
解得:x=2,y=5,
当x=2,y=5时,原式.
18.【解答】解:原式
=x﹣1.
∵x不能为0,±1,
∴当x为3时,
原式=3﹣1=2.
19.【解答】解:(1)∵每班选25名同学参加比赛,
∴(1)班C等级的人数是:25﹣6﹣12﹣5=2(人),
补充统计图如图:
(2)a=(6×100+12×90+2×80+5×70)=87.6,
∵(1)班有6人100分,12人90分,2人80分,5人70分,
∴按照从小到大的顺序将成绩排列,正中间的成绩为90分,
∴b=90,
∵由扇形统计图可知:(2)班等级为A的占44%,为最多,
∴(2)班成绩为100分的人数最多,
∴c=100,
(3)②∵(1)班和(2)班的平均成绩均为87.6分,而(1)班的众数是90分,(2)班的众数是100分,
∴从平均数和众数方面进行比较,(2)班成绩更好.
20.【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,
∴∠AEB=∠CBE,
∵BE是∠ABC的平分线,
∴∠ABE=∠CBE∠ABC,
∴∠ABE=∠AEB,
∴AE=AB,
同理可得:DF=CD,
∴AE=DF,
∴AE﹣EF=DF﹣EF,
∴AF=DE;
(2)解:∵AD=16,
∴AF+EF+DE=16,
∵AF=DE,EF=12,
∴AF+12+AF=16,
解得AF=2,
∴AB=AE=AF+EF=2+12=14,
∴ ABCD的周长为2(AB+AD)=2×(16+14)=60,即 ABCD的周长为60.
21.【解答】(1)证明:∵AE∥BD,BE∥AC,
∴四边形AEBO是平行四边形,
∵四边形ABCD是矩形,
∴AO=CO,BO=DO,AC=BD,
∴OA=OB,
∴四边形AEBO是菱形;
(2)解:∵四边形ABCD是矩形,
∴∠DAB=90°,AO=CO,BO=DO,AC=BD,
∴OA=OB=OC=DO,
∵OB=3,
∴BD=6,
由勾股定理得:AD4,
∵BO=DO,
∴S△AOB=S△AODS△BADAD×AB42=2,
∵四边形AEBO是菱形,
∴AE=AO=BO=BE=3,
∴△AEB≌△BOA(SSS),
∴△AEB的面积=△AOB的面积=2,
∴四边形AEBO的面积是22=4.
22.【解答】解:(1)设第一批每只书包的单价为x元,则第二批每只书包的单价为(x+2)元,
根据题意得:3,
解得:x=20,
经检验:x=20是分式方程的解,且符合题意,
答:第一批每只书包的单价为20元;
(2)第一批购进书包的数量=3000÷20=150(只);
第二批购进书包的数量=3×150=450(只),
答:该商店第一批购进了150只书包,第二批购进了450只书包;
(3)30×(150+450)﹣3000﹣9900=5100(元),
答:全部售出后,商店共盈利5100元.
23.【解答】解:(1)把A(1,m),B(n,1)两点坐标分别代入反比例函数,可得,,
∴m=3,n=3,
∴A(1,3),B(3,1).
把A(1,3),B(3,1)代入一次函数y=kx+b,
可得,解得,
∴直线AB的解析式为y=﹣x+4.
(2)由图象可知不等式的解集为:0<x<1或x>3.
(3)如图,过点B作BE⊥y轴于点E,过点A作AF⊥y轴于点F,
∵直线AB的解析式为y=﹣x+4,
∴M点坐标为(0,4),
∴PM=OM﹣OP=4﹣2=2,
∵A(1,3),B(3,1),
∴AF=1,BE=3,
∴四边形OPAB的面积=S△OBM﹣S△PAM
=5.
24.【解答】解:(1)根据已知条件直线和直线y=ax+5相交于点A(4,b),
∴A(4,b )代入yx,
∴b=3,
∴A(4,3),代入y=ax+5,
得a,
∴a,b=3;
(2)∵A(4,3),
∴OA,
∵QP=OA,
∴QP=5,
∵P在yx+5上,
设P(n,n+5),
∵PQ⊥x轴交yx于Q,
∴Q(n,n),
∴,
解得:n=8,
∴Q(8,6)P(8,1),
S△APQ5×4=10;
(3)如图:作ME⊥OQ于点E,
∵MD⊥PD,QM平分∠OQD,
∴ME=MD,
∵Q(8,6),O(0,0),
∴OQ=10,(根据平面直角坐标系中两点间距离公式),
由(2)可知:OD=8,QD=6,
∵S△OQD=S△OMQ+S△ODM,
∴OQ×MEMD×QDOD×QD,
10×MD+MD×6=8×6,
解得:MD=3,
∴OM=OD﹣MD=8﹣3=5,
∴M(5,0),
设直线QM为y=kx+c,
∴,
解得:,
QM为:y=2x﹣10,
∵AP、QM交于N点,
∴,
解得:,
∴N(6,2).
25.【解答】(1)证明:如图1,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠ABC=90°,
即∠BAE+∠EAD=90°,
∵四边形AEFG是正方形,
∴AE=AG,∠EAG=90°,
即∠DAG+∠EAD=90°,
∴∠BAE=∠DAG,
∴△ABE≌△ADG(SAS),
∴∠ADG=∠ABE=90°;
(2)解:由(1)知,∠ADG=90°;
∵四边形ABCD是正方形,
∴AB∥CD,∠ABC=∠ADC=90°,AB=BC,∠DBC=45°,
∴∠ADG+∠ADC=180°,
∴点C、D、G在一条直线上,
∵AB∥CD,
∴,
过点F作FN⊥BC的延长线于点N,连接CF,如图2,
∵∠ABC=90°,
∴∠1+∠2=90°,
∵四边形AEFG是正方形,
∴AE=EF,∠AEF=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
又∵∠ABE=∠ENF=90°,AE=EF,
∴△ABE≌△ENF(AAS),
∴AB=EN,BE=NF,
∵BC=AB,
∴BC=EN,
∴BC﹣CE=EN﹣CE,
即BE=CN,
∴NF=CN,
∴△FCN是等腰直角三角形,
∴∠FCN=45°,
∴∠DBC=∠FCN,
∴CF∥BD,
∴,
∴;
(3)解:CG=9DM,理由:
在BC上截取BH=DM,连接AH,ME,如图3,
∵∠ABH=∠ADM=90°,AB=AD,BH=DM,
∴△ABH≌△ADM(SAS),
∴AH=AM,∠3=∠1,
∵四边形AEFG是正方形,
∴∠EAF=45°,
即∠1+∠2=45°,
∴∠3+∠2=45°,
∴∠HAE=90°﹣45°=45°,
∴∠HAE=∠EAF,
又∵AH=AM,AE=AE,
∴△HAE≌△MAE(SAS),
∴HE=ME,
设DM=b,
∵CE=3DM,
∴CE=3b,
设正方形ABCD的边长为a,
∴BE=BC+CE=a+3b,BH=DM=b,
∴HE=BE﹣BH=a+3b﹣b=a+2b,CM=CD+DM=a+b,
∴ME=HE=a+2b,
∵∠MCE=90°,
∴由勾股定理得ME2=CM2+CE2,
∴(a+2b)2=(a+b)2+(3b)2,
解得a=3b,
∴BE=a+3b=6b,
又由(1)知△ABE≌△ADG,
∴DG=BE=6b,
∴CG=CD+DG=a+6b=3b+6b=9b,
∵DM=b,
∴CG=9DM.
21世纪教育网(www.21cnjy.com)
同课章节目录
