2025几何模型专项训练:一线三等角构造全等模型(含答案)
文档属性
| 名称 | 2025几何模型专项训练:一线三等角构造全等模型(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 112.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-26 10:28:34 | ||
图片预览


文档简介
2025几何模型专项训练:一线三等角构造全等模型
一.选择题(共10小题)
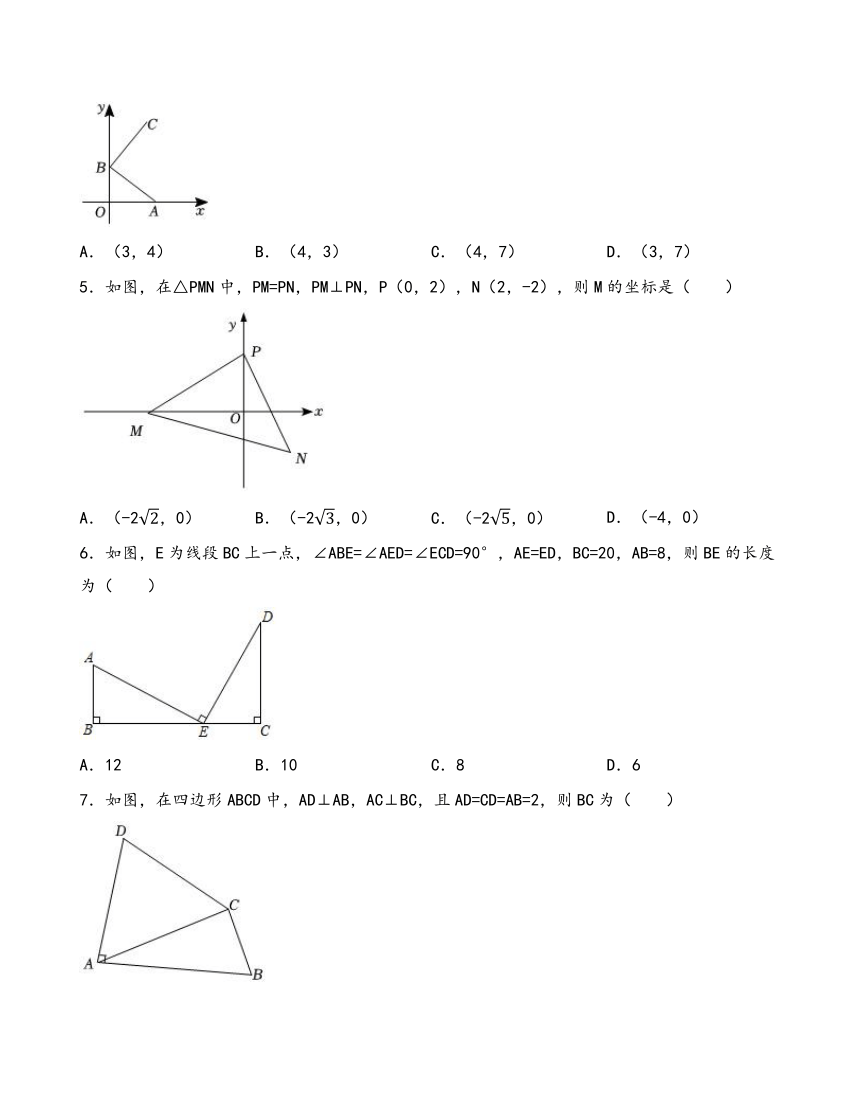
1.如图,AC=CE,∠ACE=90°,AB⊥BD,ED⊥BD,AB=6cm,DE=2cm,则BD等于( )
A.6cm B.8cm C.10cm D.4cm
2.如图,由AB=AC,∠B=∠C,便可证得△BAD≌△CAE,其全等的理由是( )
A.SSS B.SAS C.ASA D.AAS
3.如图,AC=AB=BD,∠ABD=90°,BC=8,则△BCD的面积为( )
A.8 B.12 C.14 D.16
4.如图,在平面直角坐标系中,点A的坐标是(4,0),点B的坐标是(0,3),把线段BA绕点B逆时针旋转90°后得到线段BC,则点C的坐标是( )
A.(3,4) B.(4,3) C.(4,7) D.(3,7)
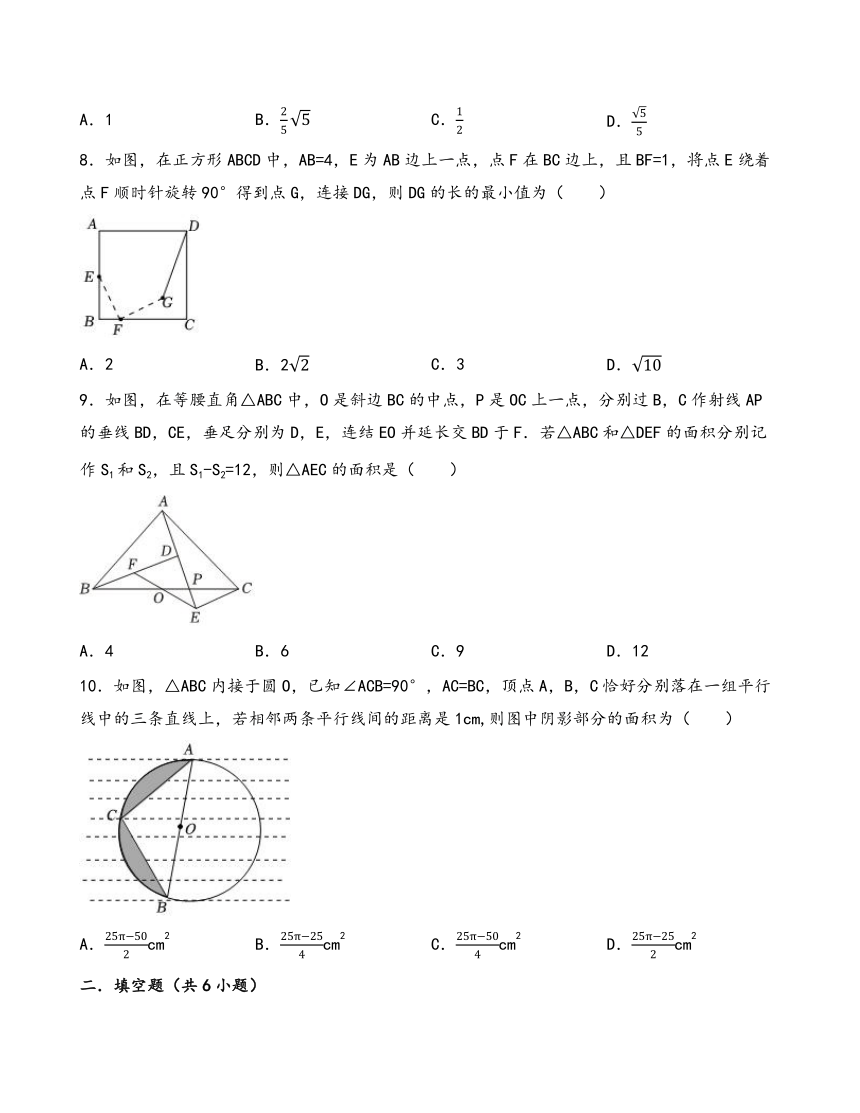
5.如图,在△PMN中,PM=PN,PM⊥PN,P(0,2),N(2,-2),则M的坐标是( )
A.(-2,0) B.(-2,0) C.(-2,0) D.(-4,0)
6.如图,E为线段BC上一点,∠ABE=∠AED=∠ECD=90°,AE=ED,BC=20,AB=8,则BE的长度为( )
A.12 B.10 C.8 D.6
7.如图,在四边形ABCD中,AD⊥AB,AC⊥BC,且AD=CD=AB=2,则BC为( )
A.1 B. C. D.
8.如图,在正方形ABCD中,AB=4,E为AB边上一点,点F在BC边上,且BF=1,将点E绕着点F顺时针旋转90°得到点G,连接DG,则DG的长的最小值为( )
A.2 B.2 C.3 D.
9.如图,在等腰直角△ABC中,O是斜边BC的中点,P是OC上一点,分别过B,C作射线AP的垂线BD,CE,垂足分别为D,E,连结EO并延长交BD于F.若△ABC和△DEF的面积分别记作S1和S2,且S1-S2=12,则△AEC的面积是( )
A.4 B.6 C.9 D.12
10.如图,△ABC内接于圆O,已知∠ACB=90°,AC=BC,顶点A,B,C恰好分别落在一组平行线中的三条直线上,若相邻两条平行线间的距离是1cm,则图中阴影部分的面积为( )
A.cm2 B.cm2 C.cm2 D.cm2
二.填空题(共6小题)
11.如图,一块含45°的三角板的一个顶点A与矩形ABCD的顶点重合,直角顶点E落在边BC上,另一顶点F恰好落在边CD的中点处,若BC=12,则AB的长为 ______.
12.如图,在Rt△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,若AD=8cm,BE=3cm,则DE=______cm.
13.如图,等边△ABC中,CH⊥AB于点H,点D、E分别在边AB、BC上,连接DE,点F在CH上,连接EF,若DE=EF,∠DEF=60°,BE=2,CE=8,则DH=______.
14.如图,在正方形ABCD中,AB=6,E是对角线AC上的一点,连结BE,过点E作EF⊥BE交AD于点F.△BCE和△AEF的面积分别为S1和S2,若2S1=3S2,则CE的长为 ______.
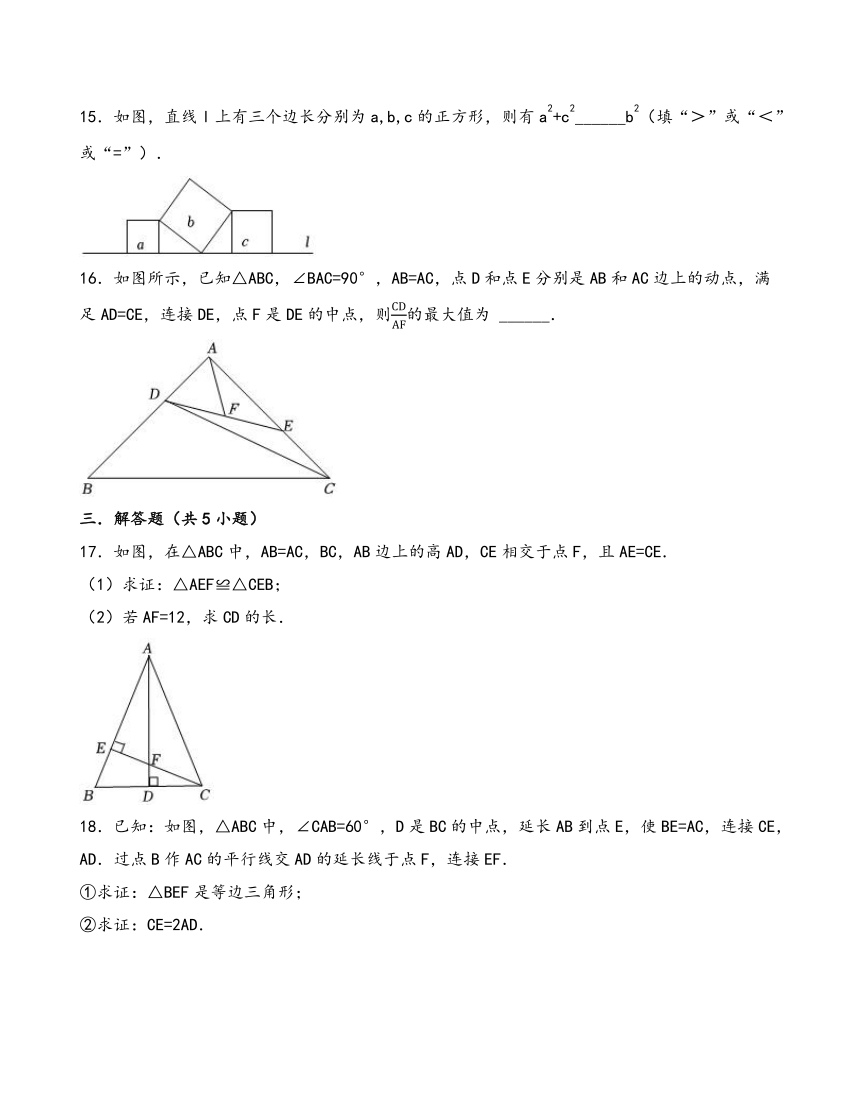
15.如图,直线l上有三个边长分别为a,b,c的正方形,则有a2+c2______b2(填“>”或“<”或“=”).
16.如图所示,已知△ABC,∠BAC=90°,AB=AC,点D和点E分别是AB和AC边上的动点,满足AD=CE,连接DE,点F是DE的中点,则的最大值为 ______.
三.解答题(共5小题)
17.如图,在△ABC中,AB=AC,BC,AB边上的高AD,CE相交于点F,且AE=CE.
(1)求证:△AEF≌△CEB;
(2)若AF=12,求CD的长.
18.已知:如图,△ABC中,∠CAB=60°,D是BC的中点,延长AB到点E,使BE=AC,连接CE,AD.过点B作AC的平行线交AD的延长线于点F,连接EF.
①求证:△BEF是等边三角形;
②求证:CE=2AD.
19.已知:如图,平面直角坐标系中,O是坐标原点,点A(2,3),点B在第四象限,△ABO中,OA=OB,∠AOB=90°.
(1)求点B的坐标;
(2)求AB直线解析式.
20.问题1:如图①,在四边形ABCD中,∠B=∠C=90°,P是BC上一点,PA=PD,AB+BP=BC.
求证:∠APD=90°;
问题2:如图②,在三角形ABC中,∠B=∠C=45°,P是AC上一点,PE=PD,且∠EPD=90°.
求的值.
21.在△ABC中,∠ACB=90°,AC=BC,过点C作直线MN,过点A作AM⊥MN于点M,过点B作BN⊥MN于点N.
(1)如图1,当直线MN在△ABC外时,证明:MN=AM+BN.
(2)如图2,当直线MN经过△ABC内部时,其他条件不变,则AM,BN与MN之间有怎样的数量关系?请说明理由.
2025几何模型专项训练:一线三等角构造全等模型
(参考答案)
一.选择题(共10小题)
1、B 2、C 3、D 4、D 5、D 6、A 7、B 8、C 9、B 10、C
二.填空题(共6小题)
11、8; 12、5; 13、1; 14、2; 15、=; 16、+1;
三.解答题(共5小题)
17、(1)证明:∵AD⊥BC,
∴∠B+∠BAD=90°,
∵CE⊥AB,
∴∠B+∠BCE=90°,
∴∠EAF=∠ECB,
在△AEF和△CEB中,
,
∴△AEF≌△CEB(ASA).
(2)解:∵△AEF≌△CEB,
∴AF=BC,
∵AB=AC,AD⊥BC,
∴CD=BD,BC=2CD,
∴AF=2CD,
∴CD=AF=×12=6.
18、证明:(1)∵BF∥AC,∴∠FBE=∠CAB=60°,∠DFB=∠DAC,在△DFB和△DAC中,
,
∴△DFB≌△DAC(AAS),
∴FB=AC,FD=AD,
∴FB=BE,
∴△BEF是等边三角形;
(2)∵∠FEA=60°,∠CAE=60°,
∴∠CAE=∠FEA,
∵EF=BE,BE=AC,
∴AC=EF,
在△ACE和△EFA中,
,
∴△ACE≌△EFA(SAS),
∴CE=FA=2AD.
19、解:(1)过A点作AC⊥y轴,垂足为C;过B点作BD⊥y轴,垂足为D,
∴∠ACO=∠BDO=90°,
∵A(2,3),
∴AC=2,OC=3,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∵∠AOC+∠CAO=90°,
∴∠BOD=∠OAC,
在△ACO和△ODB中,
,
∴△ACO≌△ODB(AAS),
∴OD=AC=2,BD=OC=3,
∴B坐标为(3,-2);
(2)设AB直线解析式为:y=kx+b,
把(2,3)(3,-2)代入y=kx+b中可得:
,
解得:,
∴AB直线解析式为:y=-5x+13.
20、问题1:证明:∵BP+PC=BC,BP+AB=BC,
∴PC=AB,
在Rt△ABP与Rt△PCD中,
,
∴Rt△ABP≌Rt△PCD(HL),
∴∠APB=∠PDC,
∴∠APD=180°-∠APB-∠DPC=180°-(∠PDC+∠DPC)=180°-90°=90°;
问题2:过D点作DF⊥AC于点F,
在ABC中,∠A=180°-∠B-∠C=90°,
∴∠A=∠PFD,
∵∠APE+∠DPF=90°∠AEP+∠APE=90°,
∴∠DPF=∠AEP,
在△APE与△FDP中,
,
∴△APE≌△FDP(AAS),
∴AE=PF,AP=DF,
在△DPF中,∠FDC=90°-∠C=90°-45°=45°,
∴DF=FC,
∴AP=FC,
∴PC=PF+FC=AE+AP,
∴.
21、证明:(1)∵AM⊥MN,BN⊥MN,∠ACB=90°,
∴∠AMC=∠CNB=90°,
∴∠MAC+∠ACM=90°,∠NCB+∠ACM=90°,
∴∠MAC=∠NCB,
在△AMC和△CNB中,
,
∴△AMC≌△CNB(AAS),
∴AM=NC,MC=BN,
∵MN=NC+MC,
∴MN=AM+BN;
(2)MN=BN-AM.
∵AM⊥MN,BN⊥MN,∠ACB=90°,
∴∠MAC+∠ACM=90°,∠NCB+∠ACM=90°,
∴∠MAC=∠NCB,
在△AMC和△CNB中,
,
∴△AMC≌△CNB(AAS),
∴AM=CN,MC=NB,
∵MN=CM-CN,
∴MN=BN-AM.
一.选择题(共10小题)
1.如图,AC=CE,∠ACE=90°,AB⊥BD,ED⊥BD,AB=6cm,DE=2cm,则BD等于( )
A.6cm B.8cm C.10cm D.4cm
2.如图,由AB=AC,∠B=∠C,便可证得△BAD≌△CAE,其全等的理由是( )
A.SSS B.SAS C.ASA D.AAS
3.如图,AC=AB=BD,∠ABD=90°,BC=8,则△BCD的面积为( )
A.8 B.12 C.14 D.16
4.如图,在平面直角坐标系中,点A的坐标是(4,0),点B的坐标是(0,3),把线段BA绕点B逆时针旋转90°后得到线段BC,则点C的坐标是( )
A.(3,4) B.(4,3) C.(4,7) D.(3,7)
5.如图,在△PMN中,PM=PN,PM⊥PN,P(0,2),N(2,-2),则M的坐标是( )
A.(-2,0) B.(-2,0) C.(-2,0) D.(-4,0)
6.如图,E为线段BC上一点,∠ABE=∠AED=∠ECD=90°,AE=ED,BC=20,AB=8,则BE的长度为( )
A.12 B.10 C.8 D.6
7.如图,在四边形ABCD中,AD⊥AB,AC⊥BC,且AD=CD=AB=2,则BC为( )
A.1 B. C. D.
8.如图,在正方形ABCD中,AB=4,E为AB边上一点,点F在BC边上,且BF=1,将点E绕着点F顺时针旋转90°得到点G,连接DG,则DG的长的最小值为( )
A.2 B.2 C.3 D.
9.如图,在等腰直角△ABC中,O是斜边BC的中点,P是OC上一点,分别过B,C作射线AP的垂线BD,CE,垂足分别为D,E,连结EO并延长交BD于F.若△ABC和△DEF的面积分别记作S1和S2,且S1-S2=12,则△AEC的面积是( )
A.4 B.6 C.9 D.12
10.如图,△ABC内接于圆O,已知∠ACB=90°,AC=BC,顶点A,B,C恰好分别落在一组平行线中的三条直线上,若相邻两条平行线间的距离是1cm,则图中阴影部分的面积为( )
A.cm2 B.cm2 C.cm2 D.cm2
二.填空题(共6小题)
11.如图,一块含45°的三角板的一个顶点A与矩形ABCD的顶点重合,直角顶点E落在边BC上,另一顶点F恰好落在边CD的中点处,若BC=12,则AB的长为 ______.
12.如图,在Rt△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D,若AD=8cm,BE=3cm,则DE=______cm.
13.如图,等边△ABC中,CH⊥AB于点H,点D、E分别在边AB、BC上,连接DE,点F在CH上,连接EF,若DE=EF,∠DEF=60°,BE=2,CE=8,则DH=______.
14.如图,在正方形ABCD中,AB=6,E是对角线AC上的一点,连结BE,过点E作EF⊥BE交AD于点F.△BCE和△AEF的面积分别为S1和S2,若2S1=3S2,则CE的长为 ______.
15.如图,直线l上有三个边长分别为a,b,c的正方形,则有a2+c2______b2(填“>”或“<”或“=”).
16.如图所示,已知△ABC,∠BAC=90°,AB=AC,点D和点E分别是AB和AC边上的动点,满足AD=CE,连接DE,点F是DE的中点,则的最大值为 ______.
三.解答题(共5小题)
17.如图,在△ABC中,AB=AC,BC,AB边上的高AD,CE相交于点F,且AE=CE.
(1)求证:△AEF≌△CEB;
(2)若AF=12,求CD的长.
18.已知:如图,△ABC中,∠CAB=60°,D是BC的中点,延长AB到点E,使BE=AC,连接CE,AD.过点B作AC的平行线交AD的延长线于点F,连接EF.
①求证:△BEF是等边三角形;
②求证:CE=2AD.
19.已知:如图,平面直角坐标系中,O是坐标原点,点A(2,3),点B在第四象限,△ABO中,OA=OB,∠AOB=90°.
(1)求点B的坐标;
(2)求AB直线解析式.
20.问题1:如图①,在四边形ABCD中,∠B=∠C=90°,P是BC上一点,PA=PD,AB+BP=BC.
求证:∠APD=90°;
问题2:如图②,在三角形ABC中,∠B=∠C=45°,P是AC上一点,PE=PD,且∠EPD=90°.
求的值.
21.在△ABC中,∠ACB=90°,AC=BC,过点C作直线MN,过点A作AM⊥MN于点M,过点B作BN⊥MN于点N.
(1)如图1,当直线MN在△ABC外时,证明:MN=AM+BN.
(2)如图2,当直线MN经过△ABC内部时,其他条件不变,则AM,BN与MN之间有怎样的数量关系?请说明理由.
2025几何模型专项训练:一线三等角构造全等模型
(参考答案)
一.选择题(共10小题)
1、B 2、C 3、D 4、D 5、D 6、A 7、B 8、C 9、B 10、C
二.填空题(共6小题)
11、8; 12、5; 13、1; 14、2; 15、=; 16、+1;
三.解答题(共5小题)
17、(1)证明:∵AD⊥BC,
∴∠B+∠BAD=90°,
∵CE⊥AB,
∴∠B+∠BCE=90°,
∴∠EAF=∠ECB,
在△AEF和△CEB中,
,
∴△AEF≌△CEB(ASA).
(2)解:∵△AEF≌△CEB,
∴AF=BC,
∵AB=AC,AD⊥BC,
∴CD=BD,BC=2CD,
∴AF=2CD,
∴CD=AF=×12=6.
18、证明:(1)∵BF∥AC,∴∠FBE=∠CAB=60°,∠DFB=∠DAC,在△DFB和△DAC中,
,
∴△DFB≌△DAC(AAS),
∴FB=AC,FD=AD,
∴FB=BE,
∴△BEF是等边三角形;
(2)∵∠FEA=60°,∠CAE=60°,
∴∠CAE=∠FEA,
∵EF=BE,BE=AC,
∴AC=EF,
在△ACE和△EFA中,
,
∴△ACE≌△EFA(SAS),
∴CE=FA=2AD.
19、解:(1)过A点作AC⊥y轴,垂足为C;过B点作BD⊥y轴,垂足为D,
∴∠ACO=∠BDO=90°,
∵A(2,3),
∴AC=2,OC=3,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∵∠AOC+∠CAO=90°,
∴∠BOD=∠OAC,
在△ACO和△ODB中,
,
∴△ACO≌△ODB(AAS),
∴OD=AC=2,BD=OC=3,
∴B坐标为(3,-2);
(2)设AB直线解析式为:y=kx+b,
把(2,3)(3,-2)代入y=kx+b中可得:
,
解得:,
∴AB直线解析式为:y=-5x+13.
20、问题1:证明:∵BP+PC=BC,BP+AB=BC,
∴PC=AB,
在Rt△ABP与Rt△PCD中,
,
∴Rt△ABP≌Rt△PCD(HL),
∴∠APB=∠PDC,
∴∠APD=180°-∠APB-∠DPC=180°-(∠PDC+∠DPC)=180°-90°=90°;
问题2:过D点作DF⊥AC于点F,
在ABC中,∠A=180°-∠B-∠C=90°,
∴∠A=∠PFD,
∵∠APE+∠DPF=90°∠AEP+∠APE=90°,
∴∠DPF=∠AEP,
在△APE与△FDP中,
,
∴△APE≌△FDP(AAS),
∴AE=PF,AP=DF,
在△DPF中,∠FDC=90°-∠C=90°-45°=45°,
∴DF=FC,
∴AP=FC,
∴PC=PF+FC=AE+AP,
∴.
21、证明:(1)∵AM⊥MN,BN⊥MN,∠ACB=90°,
∴∠AMC=∠CNB=90°,
∴∠MAC+∠ACM=90°,∠NCB+∠ACM=90°,
∴∠MAC=∠NCB,
在△AMC和△CNB中,
,
∴△AMC≌△CNB(AAS),
∴AM=NC,MC=BN,
∵MN=NC+MC,
∴MN=AM+BN;
(2)MN=BN-AM.
∵AM⊥MN,BN⊥MN,∠ACB=90°,
∴∠MAC+∠ACM=90°,∠NCB+∠ACM=90°,
∴∠MAC=∠NCB,
在△AMC和△CNB中,
,
∴△AMC≌△CNB(AAS),
∴AM=CN,MC=NB,
∵MN=CM-CN,
∴MN=BN-AM.
同课章节目录
