【江苏省各地区真题汇编】反比例函数核心考点检测卷-2025年中考数学
文档属性
| 名称 | 【江苏省各地区真题汇编】反比例函数核心考点检测卷-2025年中考数学 |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-26 09:25:59 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
【江苏省各地区真题汇编】反比例函数核心考点检测卷-2025年中考数学
一.选择题(共8小题)
1.(2025春 沛县月考)下列函数中,表示y是x的反比例函数的是( )
A. B. C.y=2x D.y=x+2
2.(2025 东台市一模)对于反比例函数,下列说法错误的是( )
A.图象经过点(3,﹣675)
B.图象位于第二、四象限
C.当x<0时,y随x的增大而减小
D.当x>0时,y随x的增大而增大
3.(2025 姑苏区校级模拟)如图,在平面直角坐标系中,点A(0,2),B(1,0),∠ABC=90°,BC=2AB,若点C在函数y(x>0)的图象上,则k的值为( )
A.6 B.8 C.10 D.12
4.(2025 徐州校级模拟)如图,四边形AOBC是平行四边形,点B在x轴上,CA的延长线与y轴交于点D,反比例函数的图象经过点A(2,y),且与边BC交于点E.若S平行四边形AOBC=6,且AD=AC,则点E的纵坐标为( )
A. B. C. D.
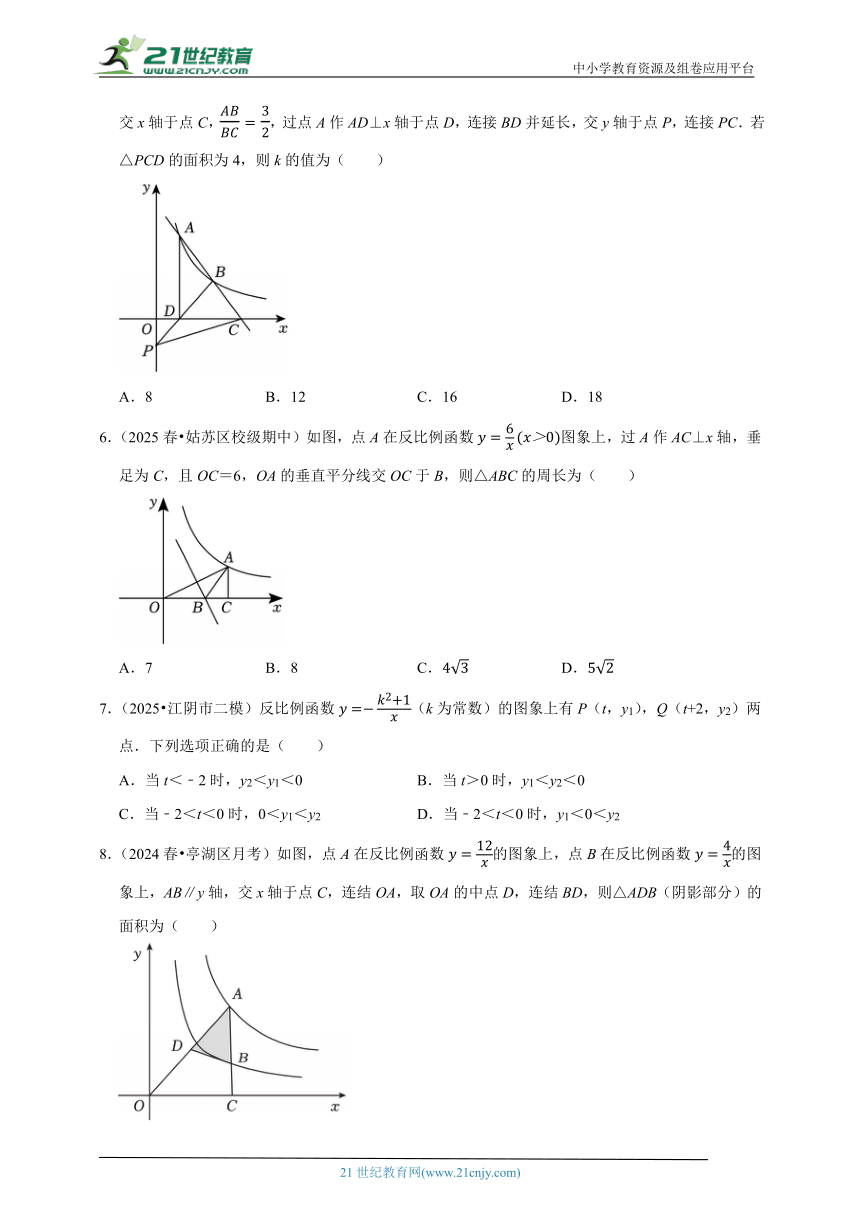
5.(2025 沭阳县校级二模)如图,直线y=mx+n交反比例函数y(x>0)的图象于点A和点B,交x轴于点C,,过点A作AD⊥x轴于点D,连接BD并延长,交y轴于点P,连接PC.若△PCD的面积为4,则k的值为( )
A.8 B.12 C.16 D.18
6.(2025春 姑苏区校级期中)如图,点A在反比例函数图象上,过A作AC⊥x轴,垂足为C,且OC=6,OA的垂直平分线交OC于B,则△ABC的周长为( )
A.7 B.8 C. D.
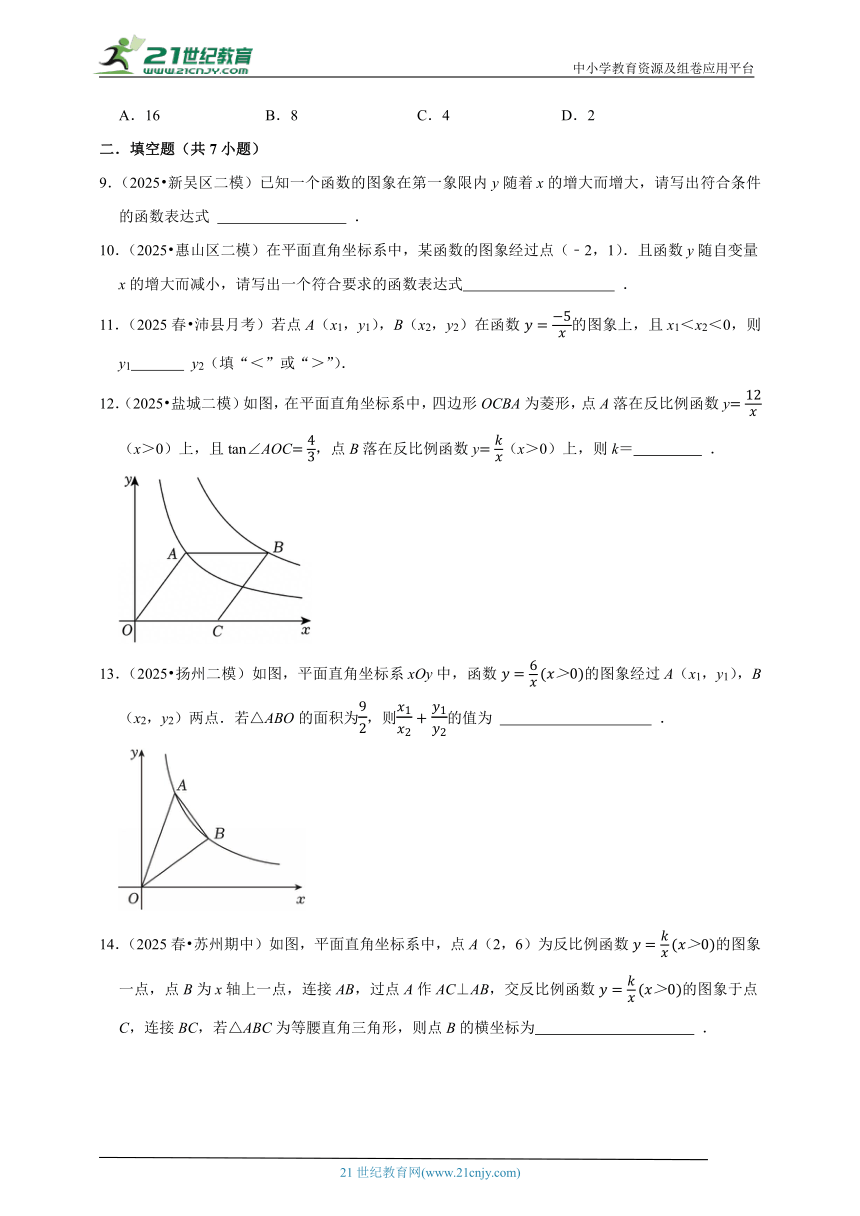
7.(2025 江阴市二模)反比例函数(k为常数)的图象上有P(t,y1),Q(t+2,y2)两点.下列选项正确的是( )
A.当t<﹣2时,y2<y1<0 B.当t>0时,y1<y2<0
C.当﹣2<t<0时,0<y1<y2 D.当﹣2<t<0时,y1<0<y2
8.(2024春 亭湖区月考)如图,点A在反比例函数的图象上,点B在反比例函数的图象上,AB∥y轴,交x轴于点C,连结OA,取OA的中点D,连结BD,则△ADB(阴影部分)的面积为( )
A.16 B.8 C.4 D.2
二.填空题(共7小题)
9.(2025 新吴区二模)已知一个函数的图象在第一象限内y随着x的增大而增大,请写出符合条件的函数表达式 .
10.(2025 惠山区二模)在平面直角坐标系中,某函数的图象经过点(﹣2,1).且函数y随自变量x的增大而减小,请写出一个符合要求的函数表达式 .
11.(2025春 沛县月考)若点A(x1,y1),B(x2,y2)在函数的图象上,且x1<x2<0,则y1 y2(填“<”或“>”).
12.(2025 盐城二模)如图,在平面直角坐标系中,四边形OCBA为菱形,点A落在反比例函数y(x>0)上,且tan∠AOC,点B落在反比例函数y(x>0)上,则k= .
13.(2025 扬州二模)如图,平面直角坐标系xOy中,函数的图象经过A(x1,y1),B(x2,y2)两点.若△ABO的面积为,则的值为 .
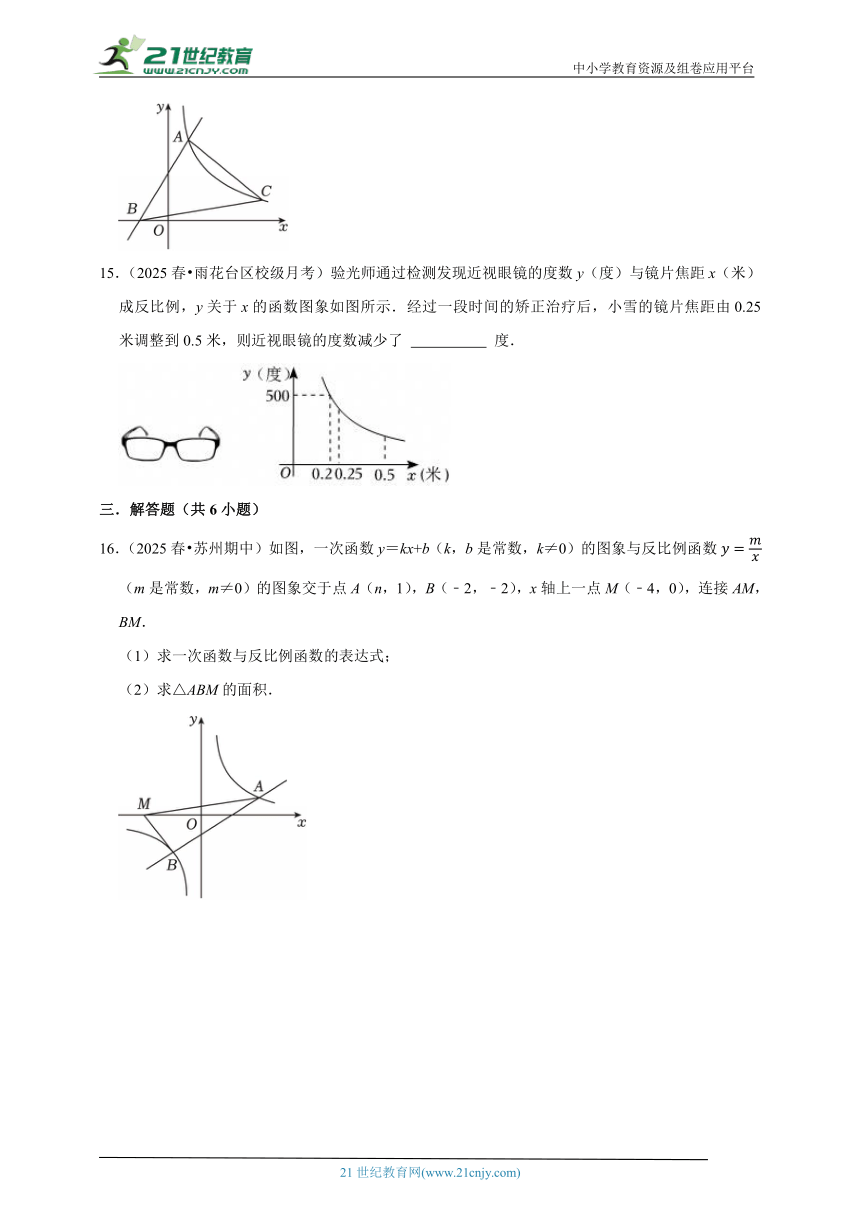
14.(2025春 苏州期中)如图,平面直角坐标系中,点A(2,6)为反比例函数的图象一点,点B为x轴上一点,连接AB,过点A作AC⊥AB,交反比例函数的图象于点C,连接BC,若△ABC为等腰直角三角形,则点B的横坐标为 .
15.(2025春 雨花台区校级月考)验光师通过检测发现近视眼镜的度数y(度)与镜片焦距x(米)成反比例,y关于x的函数图象如图所示.经过一段时间的矫正治疗后,小雪的镜片焦距由0.25米调整到0.5米,则近视眼镜的度数减少了 度.
三.解答题(共6小题)
16.(2025春 苏州期中)如图,一次函数y=kx+b(k,b是常数,k≠0)的图象与反比例函数(m是常数,m≠0)的图象交于点A(n,1),B(﹣2,﹣2),x轴上一点M(﹣4,0),连接AM,BM.
(1)求一次函数与反比例函数的表达式;
(2)求△ABM的面积.
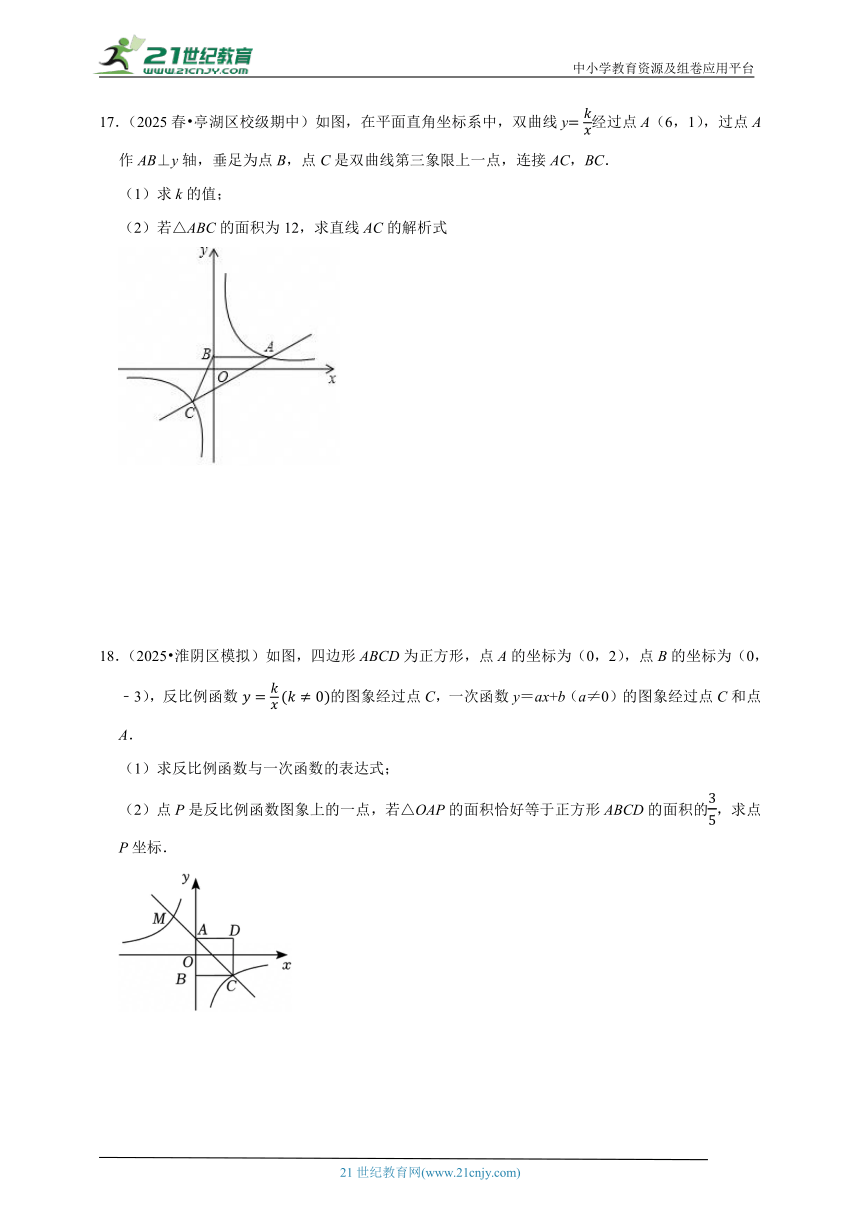
17.(2025春 亭湖区校级期中)如图,在平面直角坐标系中,双曲线y经过点A(6,1),过点A作AB⊥y轴,垂足为点B,点C是双曲线第三象限上一点,连接AC,BC.
(1)求k的值;
(2)若△ABC的面积为12,求直线AC的解析式
18.(2025 淮阴区模拟)如图,四边形ABCD为正方形,点A的坐标为(0,2),点B的坐标为(0,﹣3),反比例函数的图象经过点C,一次函数y=ax+b(a≠0)的图象经过点C和点A.
(1)求反比例函数与一次函数的表达式;
(2)点P是反比例函数图象上的一点,若△OAP的面积恰好等于正方形ABCD的面积的,求点P坐标.
19.(2025春 兴化市期中)反比例函数的图象经过点A(1,2a)和点B(5﹣a,3).
(1)求a、k的值;
(2)如图①,在反比例函数的图象上有一点P,小明发现将点P绕原点O顺时针方向旋转90°后得到的点Q在另一个反比例函数图象上,求出点Q所在的函数表达式,并写出自变量取值范围;
(3)如图②,已知直线l1:y=x和l2:y=﹣x,将反比例函数的图象绕原点旋转45°后得到新图象,在新图象上任取一点Q,过点Q作QM⊥l1,QN⊥l2,垂足分别为点M,点N.求四边形QMON的面积.
20.(2025 苏州一模)如图,已知一次函数的图象与反比例函数的图象相交于点A,点B(点A在点B的左侧).连接OA,过点B作BD⊥y轴,垂足为D,与OA交于点C.
(1)当点B的坐标为(6,n)时,求k的值;
(2)当时,求线段OD的长.
21.(2024春 鼓楼区校级期末)如图,已知正比例函数的图象与反比例函数的图象相交于点A(3,n)和点 B.
(1)求反比例函数的解析式;
(2)请结合函数图象,直接写出不等式的解集;
(3)如图,以AO为边作菱形AOCD,使点C在x轴正半轴上,点D在第一象限,双曲线交CD于点E,连接AE、OE,求△AOE的面积.
【江苏省各地区真题汇编】反比例函数核心考点检测卷-2025年中考数学
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B C C A B A B D
一.选择题(共8小题)
1.(2025春 沛县月考)下列函数中,表示y是x的反比例函数的是( )
A. B. C.y=2x D.y=x+2
【解答】解:A. 表示y是x的正比例函数,不符合题意;
B. 表示y是x的反比例函数,符合题意;
C.y=2x 表示y是x的正比例函数,不符合题意;
D.y=x+2表示y是x的一次函数,不符合题意;
故选:B.
2.(2025 东台市一模)对于反比例函数,下列说法错误的是( )
A.图象经过点(3,﹣675)
B.图象位于第二、四象限
C.当x<0时,y随x的增大而减小
D.当x>0时,y随x的增大而增大
【解答】解:A、把x=3代入得,y=﹣675,则(3,﹣675)在图象上,选项正确,不符合题意;
B、图象位于第二、四象限,选项正确,不符合题意;
C、当x<0时,y随x的增大而增大,选项错误,符合题意;
D、当x>0时,y随x的增大而增大,选项正确,不符合题意.
故选:C.
3.(2025 姑苏区校级模拟)如图,在平面直角坐标系中,点A(0,2),B(1,0),∠ABC=90°,BC=2AB,若点C在函数y(x>0)的图象上,则k的值为( )
A.6 B.8 C.10 D.12
【解答】解:作CD⊥x轴,垂足为点D,
∵点A(0,2),B(1,0),
∴OA=2,OB=1,
∵∠AOB=∠BDC,∠ABO=∠BCD,
∴△AOB∽△BDC,
∵BC=2AB,
∴,
∴BD=2AO=4,CD=2BO=2,
∴OD=5,
∴C(5,2),
∵点C在函数y(x>0)的图象上,
∴k=5×2=10.
故选:C.
4.(2025 徐州校级模拟)如图,四边形AOBC是平行四边形,点B在x轴上,CA的延长线与y轴交于点D,反比例函数的图象经过点A(2,y),且与边BC交于点E.若S平行四边形AOBC=6,且AD=AC,则点E的纵坐标为( )
A. B. C. D.
【解答】解:∵AD=AC,且A(2,y),
∴AC=2,
又∵S平行四边形AOBC=AC y=6,
∴y=3,
则k=2×3=6,
反比例函数解析式为:y(x>0),
∵四边形AOBC是平行四边形,
∴OB=CA=2,
∴B(2,0),C(4,3),
∴直线BC:y,
联立,
解得:y1(1),y2(1)(舍去),
故选:A.
5.(2025 沭阳县校级二模)如图,直线y=mx+n交反比例函数y(x>0)的图象于点A和点B,交x轴于点C,,过点A作AD⊥x轴于点D,连接BD并延长,交y轴于点P,连接PC.若△PCD的面积为4,则k的值为( )
A.8 B.12 C.16 D.18
【解答】解:过点B分别作BM⊥AD于点M,BN⊥CD于点N,
设点B(a,b),k=ab,
则BN∥AD,则△CNB∽△CDA,
则,即,
∴ADb,
则k=abb xA,则xAa,
则点A(a,b),则点D(a,0),
由点B、D的坐标得,直线BD的表达式为:yxb,
则点P(0,b);
由点A、B的坐标得,直线AB的表达式为:yb,
则点C(,0)则CD=a,
∵S△PCDCD OPa b=4,
则ab=12=k,
故选:B.
6.(2025春 姑苏区校级期中)如图,点A在反比例函数图象上,过A作AC⊥x轴,垂足为C,且OC=6,OA的垂直平分线交OC于B,则△ABC的周长为( )
A.7 B.8 C. D.
【解答】解:∵点A在反比例函数图象上,
∴S△AOC3,
∵3,OC=6,
∴AC=1,
∵OA的垂直平分线交OC于B,
∴AB=OB,
∴△ABC的周长=OC+AC=6+1=7.
故选:A.
7.(2025 江阴市二模)反比例函数(k为常数)的图象上有P(t,y1),Q(t+2,y2)两点.下列选项正确的是( )
A.当t<﹣2时,y2<y1<0 B.当t>0时,y1<y2<0
C.当﹣2<t<0时,0<y1<y2 D.当﹣2<t<0时,y1<0<y2
【解答】解:根据反比例函数的图象和性质逐项分析判断如下:
由条件可知﹣(k2+1)<0,
∴的图象在第二、第四象限内,在每个象限,y随x增大而增大,
当t<﹣2时,则t+2<0,
∴P(t,y1),Q(t+2,y2)都在第二象限,
∴0<y1<y2,故A选项错误,不符合题意;
当t>0时,则t+2>0,
∴P(t,y1),Q(t+2,y2)都在第四象限,
∴y1<y2<0,故B选项正确,符合题意;
当﹣2<t<0时,t+2>0,P(t,y1)在第二象限,Q(t+2,y2)在第四象限,
∴y1>0>y2,故C选项错误,不符合题意;D选项错误,不符合题意;
故选:B.
8.(2024春 亭湖区月考)如图,点A在反比例函数的图象上,点B在反比例函数的图象上,AB∥y轴,交x轴于点C,连结OA,取OA的中点D,连结BD,则△ADB(阴影部分)的面积为( )
A.16 B.8 C.4 D.2
【解答】解:∵点A在反比例函数的图象上,
∴S△AOC,
∵点B在反比例函数的图象上,
∴S△BOC2,
∴S△AOB=S△AOC﹣S△BOC=6﹣2=4,
∵D是OA的中点,
∴S阴影S△AOB2.
故选:D.
二.填空题(共7小题)
9.(2025 新吴区二模)已知一个函数的图象在第一象限内y随着x的增大而增大,请写出符合条件的函数表达式 y=x(答案不唯一) .
【解答】解:∵一个函数的图象在第一象限内y随着x的增大而增大,
∴函数关系式可以是:y=x或y=x2(答案不唯一).
故答案为:y=x(答案不唯一).
10.(2025 惠山区二模)在平面直角坐标系中,某函数的图象经过点(﹣2,1).且函数y随自变量x的增大而减小,请写出一个符合要求的函数表达式 y=﹣x﹣1(答案不唯一) .
【解答】解:由题意得k<0,设y=﹣x+b,
∵图象经过点(﹣2,1),
∴1=﹣(﹣2)+b,
解得:b=﹣1,
∴函数表达式为y=﹣x﹣1.
故答案为:y=﹣x﹣1(答案不唯一).
11.(2025春 沛县月考)若点A(x1,y1),B(x2,y2)在函数的图象上,且x1<x2<0,则y1 < y2(填“<”或“>”).
【解答】解:∵k=﹣5<0,
∴反比例函数的图象在第二、四象限,
∴在每一个象限内y随x的增大而增大,
∵x1<x2<0,
∴y1<y2.
故答案为:<.
12.(2025 盐城二模)如图,在平面直角坐标系中,四边形OCBA为菱形,点A落在反比例函数y(x>0)上,且tan∠AOC,点B落在反比例函数y(x>0)上,则k= 32 .
【解答】解:过点A、B作x轴的垂线,垂足分别为D、E,
∵tan∠AOC,
∴,
∴设AD=4a,则OD=3a,
∴点A(3a,4a),
由题意可得:3a 4a=12,
∴a=1(负值已舍),
∴点A(3,4),
∴AD=4,OD=3,
∴OA5,
∵,AB∥CO,
∴点B(8,4),
∵点B落在反比例函数y(x>0)上,
∴k=8×4=32,
故答案为:32.
13.(2025 扬州二模)如图,平面直角坐标系xOy中,函数的图象经过A(x1,y1),B(x2,y2)两点.若△ABO的面积为,则的值为 .
【解答】解:如图,作AD⊥x轴,BC⊥x轴,垂足分别为D、C,
根据反比例函数k值的几何意义可得:
S△AOB=S梯形ABCD,
∴(y1+y2)(x2﹣x1),
整理得:x2y1﹣x1y2=9,
∵x1y1 x2y2=36,
∴x1y2 x2y1=36,
∴(x2y1﹣9)x2y1=36,
解得x2y1=12,
∴.
故答案为:.
14.(2025春 苏州期中)如图,平面直角坐标系中,点A(2,6)为反比例函数的图象一点,点B为x轴上一点,连接AB,过点A作AC⊥AB,交反比例函数的图象于点C,连接BC,若△ABC为等腰直角三角形,则点B的横坐标为 .
【解答】解:作AM⊥x轴于M,CD⊥x轴于D,CN⊥AM于N,
∵A(2,6),
∴OM=2,AM=6,
∵点A(2,6)为反比例函数的图象一点,
∴k=2×6=12,
∴反比例函数为y,
设C(a,),则OD=a,CD,
∵AC⊥AB,
∴∠BAM+∠CAN=90°,
∵∠ABM+∠BAM=90°,
∴∠ABM=∠CAN,
∵∠AMB=∠CNA=90°,AB=AC,
∴△AMB≌△CAN(AAS),
∴BM=AN=6,CN=AM=6,
∴OD=OM+MD=OD+CN,
∴a=2+6=8,
∴BM=6,
∴OB=BM﹣OM2,
∴B点的横坐标为,
故答案为:.
15.(2025春 雨花台区校级月考)验光师通过检测发现近视眼镜的度数y(度)与镜片焦距x(米)成反比例,y关于x的函数图象如图所示.经过一段时间的矫正治疗后,小雪的镜片焦距由0.25米调整到0.5米,则近视眼镜的度数减少了 200 度.
【解答】解:设y(k≠0),
把(0.2,500)代入y(k≠0),
∴k=500×0.2=100,
∴函数解析式为y,
当x=0.25时,y400,
当x=0.5时,y200,
∴度数减少了400﹣200=200(度),
故答案为:200.
三.解答题(共6小题)
16.(2025春 苏州期中)如图,一次函数y=kx+b(k,b是常数,k≠0)的图象与反比例函数(m是常数,m≠0)的图象交于点A(n,1),B(﹣2,﹣2),x轴上一点M(﹣4,0),连接AM,BM.
(1)求一次函数与反比例函数的表达式;
(2)求△ABM的面积.
【解答】解:(1)∵两个函数图象交于点A(n,1),B(﹣2,﹣2),
∴m=﹣2×(﹣2)=4,
∴反比例函数解析式为y,
∵点A(4,1)和B(﹣2,﹣2)在一次函数y=kx+b(k,b是常数,k≠0)的图象上,
,解得,
∴一次函数解析式为y1.
(2)如图,直线AB交x轴于点C,
在直线y1中,当y=0时,x=2,
∴C(2,0),
∴CM=6,
∴S△ABM=S△AMC+S△BMC9.
17.(2025春 亭湖区校级期中)如图,在平面直角坐标系中,双曲线y经过点A(6,1),过点A作AB⊥y轴,垂足为点B,点C是双曲线第三象限上一点,连接AC,BC.
(1)求k的值;
(2)若△ABC的面积为12,求直线AC的解析式
【解答】解:(1)∵双曲线y,经过点A(6,1),
∴1,
解得k=6;
(2)设点C到AB的距离为h,
∵点A的坐标为(6,1),AB⊥y轴,
∴AB=6,
∴S△ABC6 h=12,
解得h=4,
∵点A的纵坐标为1,
∴点C的纵坐标为1﹣4=﹣3,
∴3,
解得x=﹣2,
∴点C的坐标为(﹣2,﹣3),
设直线AC的解析式为y=kx+b,
则,解得,
所以,直线AC的解析式为yx﹣2.
18.(2025 淮阴区模拟)如图,四边形ABCD为正方形,点A的坐标为(0,2),点B的坐标为(0,﹣3),反比例函数的图象经过点C,一次函数y=ax+b(a≠0)的图象经过点C和点A.
(1)求反比例函数与一次函数的表达式;
(2)点P是反比例函数图象上的一点,若△OAP的面积恰好等于正方形ABCD的面积的,求点P坐标.
【解答】(1)解:∵A(0,2),B(0,﹣3),
∴BC=AB=5,
∴C(5,﹣3),
把C(5,﹣3)代入y得:﹣3,
∴k=﹣3×5=﹣15,
∴反比例函数解析式为y;
把A(0,2),C(5,﹣3)代入一次函数y=ax+b得:
,
解得,
∴一次函数解析式为y=﹣x+2;
(2)设P点的坐标为(x,y),
∵S△OAPS正方形ABCD,
∴丨x丨=25,
解得:x=±15,
当x=15时,y=﹣1;
当x=﹣15时;y=1
∴P(15,﹣1)或(﹣15,1).
19.(2025春 兴化市期中)反比例函数的图象经过点A(1,2a)和点B(5﹣a,3).
(1)求a、k的值;
(2)如图①,在反比例函数的图象上有一点P,小明发现将点P绕原点O顺时针方向旋转90°后得到的点Q在另一个反比例函数图象上,求出点Q所在的函数表达式,并写出自变量取值范围;
(3)如图②,已知直线l1:y=x和l2:y=﹣x,将反比例函数的图象绕原点旋转45°后得到新图象,在新图象上任取一点Q,过点Q作QM⊥l1,QN⊥l2,垂足分别为点M,点N.求四边形QMON的面积.
【解答】解:(1)将点A、B的坐标代入反比例函数表达式得:k=2a=3(5﹣a),
则a=3,k=6;
(2)设点P(m,n),则mn=6,则点Q(n,﹣m),
则﹣mn=﹣6,
则点Q所在的函数表达式为y(x>0);
(3)将直线l1:y=x、l2:y=﹣x,反比例函数的图象绕原点逆时针旋转45°,
则OM、ON、反比例函数分别和y轴、x轴、原反比例函数重合,
则四边形QMON的面积=k=6.
20.(2025 苏州一模)如图,已知一次函数的图象与反比例函数的图象相交于点A,点B(点A在点B的左侧).连接OA,过点B作BD⊥y轴,垂足为D,与OA交于点C.
(1)当点B的坐标为(6,n)时,求k的值;
(2)当时,求线段OD的长.
【解答】解:(1)把点B的坐标为(6,n)代入得n4=1,
∴B(6,1),
把B(6,1)代入得1,
∴k=6;
(2)过B作BH⊥x轴于H,
∵BD⊥y轴,
∴∠BDO=∠DOH=∠BHO=90°,
∴四边形BDOH是矩形,
∴OD=BH,
过A作AE⊥y轴于E,
∴CD∥AE,
∴△OCD∽△OAE,
∴,
∵,
∴,
解得,,
∴B(4,),A(4,),
∴OD,OE,
∵OE=4OD,
∴4,
∴k,
∴OD.
21.(2024春 鼓楼区校级期末)如图,已知正比例函数的图象与反比例函数的图象相交于点A(3,n)和点 B.
(1)求反比例函数的解析式;
(2)请结合函数图象,直接写出不等式的解集;
(3)如图,以AO为边作菱形AOCD,使点C在x轴正半轴上,点D在第一象限,双曲线交CD于点E,连接AE、OE,求△AOE的面积.
【解答】解:(1)把点A(3,n)代入正比例函数可得:n=4,
∴点A(3,4),
把点A(3,4)代入反比例函数,
可得:k=3×4=12,
∴反比例函数的解析式为;
(2)∵点A与点B是关于原点对称的,
∴点B(﹣3,﹣4),
∴根据图象可得,不等式的解集为:x<﹣3或0<x<3;
(3)如图所示,过点A作AG⊥x轴,垂足为G,
∵A(3,4),
∴OG=3,AG=4,
在Rt△AOG中,,
∵四边形AOCD是菱形,
∴OC=OA=5,,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【江苏省各地区真题汇编】反比例函数核心考点检测卷-2025年中考数学
一.选择题(共8小题)
1.(2025春 沛县月考)下列函数中,表示y是x的反比例函数的是( )
A. B. C.y=2x D.y=x+2
2.(2025 东台市一模)对于反比例函数,下列说法错误的是( )
A.图象经过点(3,﹣675)
B.图象位于第二、四象限
C.当x<0时,y随x的增大而减小
D.当x>0时,y随x的增大而增大
3.(2025 姑苏区校级模拟)如图,在平面直角坐标系中,点A(0,2),B(1,0),∠ABC=90°,BC=2AB,若点C在函数y(x>0)的图象上,则k的值为( )
A.6 B.8 C.10 D.12
4.(2025 徐州校级模拟)如图,四边形AOBC是平行四边形,点B在x轴上,CA的延长线与y轴交于点D,反比例函数的图象经过点A(2,y),且与边BC交于点E.若S平行四边形AOBC=6,且AD=AC,则点E的纵坐标为( )
A. B. C. D.
5.(2025 沭阳县校级二模)如图,直线y=mx+n交反比例函数y(x>0)的图象于点A和点B,交x轴于点C,,过点A作AD⊥x轴于点D,连接BD并延长,交y轴于点P,连接PC.若△PCD的面积为4,则k的值为( )
A.8 B.12 C.16 D.18
6.(2025春 姑苏区校级期中)如图,点A在反比例函数图象上,过A作AC⊥x轴,垂足为C,且OC=6,OA的垂直平分线交OC于B,则△ABC的周长为( )
A.7 B.8 C. D.
7.(2025 江阴市二模)反比例函数(k为常数)的图象上有P(t,y1),Q(t+2,y2)两点.下列选项正确的是( )
A.当t<﹣2时,y2<y1<0 B.当t>0时,y1<y2<0
C.当﹣2<t<0时,0<y1<y2 D.当﹣2<t<0时,y1<0<y2
8.(2024春 亭湖区月考)如图,点A在反比例函数的图象上,点B在反比例函数的图象上,AB∥y轴,交x轴于点C,连结OA,取OA的中点D,连结BD,则△ADB(阴影部分)的面积为( )
A.16 B.8 C.4 D.2
二.填空题(共7小题)
9.(2025 新吴区二模)已知一个函数的图象在第一象限内y随着x的增大而增大,请写出符合条件的函数表达式 .
10.(2025 惠山区二模)在平面直角坐标系中,某函数的图象经过点(﹣2,1).且函数y随自变量x的增大而减小,请写出一个符合要求的函数表达式 .
11.(2025春 沛县月考)若点A(x1,y1),B(x2,y2)在函数的图象上,且x1<x2<0,则y1 y2(填“<”或“>”).
12.(2025 盐城二模)如图,在平面直角坐标系中,四边形OCBA为菱形,点A落在反比例函数y(x>0)上,且tan∠AOC,点B落在反比例函数y(x>0)上,则k= .
13.(2025 扬州二模)如图,平面直角坐标系xOy中,函数的图象经过A(x1,y1),B(x2,y2)两点.若△ABO的面积为,则的值为 .
14.(2025春 苏州期中)如图,平面直角坐标系中,点A(2,6)为反比例函数的图象一点,点B为x轴上一点,连接AB,过点A作AC⊥AB,交反比例函数的图象于点C,连接BC,若△ABC为等腰直角三角形,则点B的横坐标为 .
15.(2025春 雨花台区校级月考)验光师通过检测发现近视眼镜的度数y(度)与镜片焦距x(米)成反比例,y关于x的函数图象如图所示.经过一段时间的矫正治疗后,小雪的镜片焦距由0.25米调整到0.5米,则近视眼镜的度数减少了 度.
三.解答题(共6小题)
16.(2025春 苏州期中)如图,一次函数y=kx+b(k,b是常数,k≠0)的图象与反比例函数(m是常数,m≠0)的图象交于点A(n,1),B(﹣2,﹣2),x轴上一点M(﹣4,0),连接AM,BM.
(1)求一次函数与反比例函数的表达式;
(2)求△ABM的面积.
17.(2025春 亭湖区校级期中)如图,在平面直角坐标系中,双曲线y经过点A(6,1),过点A作AB⊥y轴,垂足为点B,点C是双曲线第三象限上一点,连接AC,BC.
(1)求k的值;
(2)若△ABC的面积为12,求直线AC的解析式
18.(2025 淮阴区模拟)如图,四边形ABCD为正方形,点A的坐标为(0,2),点B的坐标为(0,﹣3),反比例函数的图象经过点C,一次函数y=ax+b(a≠0)的图象经过点C和点A.
(1)求反比例函数与一次函数的表达式;
(2)点P是反比例函数图象上的一点,若△OAP的面积恰好等于正方形ABCD的面积的,求点P坐标.
19.(2025春 兴化市期中)反比例函数的图象经过点A(1,2a)和点B(5﹣a,3).
(1)求a、k的值;
(2)如图①,在反比例函数的图象上有一点P,小明发现将点P绕原点O顺时针方向旋转90°后得到的点Q在另一个反比例函数图象上,求出点Q所在的函数表达式,并写出自变量取值范围;
(3)如图②,已知直线l1:y=x和l2:y=﹣x,将反比例函数的图象绕原点旋转45°后得到新图象,在新图象上任取一点Q,过点Q作QM⊥l1,QN⊥l2,垂足分别为点M,点N.求四边形QMON的面积.
20.(2025 苏州一模)如图,已知一次函数的图象与反比例函数的图象相交于点A,点B(点A在点B的左侧).连接OA,过点B作BD⊥y轴,垂足为D,与OA交于点C.
(1)当点B的坐标为(6,n)时,求k的值;
(2)当时,求线段OD的长.
21.(2024春 鼓楼区校级期末)如图,已知正比例函数的图象与反比例函数的图象相交于点A(3,n)和点 B.
(1)求反比例函数的解析式;
(2)请结合函数图象,直接写出不等式的解集;
(3)如图,以AO为边作菱形AOCD,使点C在x轴正半轴上,点D在第一象限,双曲线交CD于点E,连接AE、OE,求△AOE的面积.
【江苏省各地区真题汇编】反比例函数核心考点检测卷-2025年中考数学
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B C C A B A B D
一.选择题(共8小题)
1.(2025春 沛县月考)下列函数中,表示y是x的反比例函数的是( )
A. B. C.y=2x D.y=x+2
【解答】解:A. 表示y是x的正比例函数,不符合题意;
B. 表示y是x的反比例函数,符合题意;
C.y=2x 表示y是x的正比例函数,不符合题意;
D.y=x+2表示y是x的一次函数,不符合题意;
故选:B.
2.(2025 东台市一模)对于反比例函数,下列说法错误的是( )
A.图象经过点(3,﹣675)
B.图象位于第二、四象限
C.当x<0时,y随x的增大而减小
D.当x>0时,y随x的增大而增大
【解答】解:A、把x=3代入得,y=﹣675,则(3,﹣675)在图象上,选项正确,不符合题意;
B、图象位于第二、四象限,选项正确,不符合题意;
C、当x<0时,y随x的增大而增大,选项错误,符合题意;
D、当x>0时,y随x的增大而增大,选项正确,不符合题意.
故选:C.
3.(2025 姑苏区校级模拟)如图,在平面直角坐标系中,点A(0,2),B(1,0),∠ABC=90°,BC=2AB,若点C在函数y(x>0)的图象上,则k的值为( )
A.6 B.8 C.10 D.12
【解答】解:作CD⊥x轴,垂足为点D,
∵点A(0,2),B(1,0),
∴OA=2,OB=1,
∵∠AOB=∠BDC,∠ABO=∠BCD,
∴△AOB∽△BDC,
∵BC=2AB,
∴,
∴BD=2AO=4,CD=2BO=2,
∴OD=5,
∴C(5,2),
∵点C在函数y(x>0)的图象上,
∴k=5×2=10.
故选:C.
4.(2025 徐州校级模拟)如图,四边形AOBC是平行四边形,点B在x轴上,CA的延长线与y轴交于点D,反比例函数的图象经过点A(2,y),且与边BC交于点E.若S平行四边形AOBC=6,且AD=AC,则点E的纵坐标为( )
A. B. C. D.
【解答】解:∵AD=AC,且A(2,y),
∴AC=2,
又∵S平行四边形AOBC=AC y=6,
∴y=3,
则k=2×3=6,
反比例函数解析式为:y(x>0),
∵四边形AOBC是平行四边形,
∴OB=CA=2,
∴B(2,0),C(4,3),
∴直线BC:y,
联立,
解得:y1(1),y2(1)(舍去),
故选:A.
5.(2025 沭阳县校级二模)如图,直线y=mx+n交反比例函数y(x>0)的图象于点A和点B,交x轴于点C,,过点A作AD⊥x轴于点D,连接BD并延长,交y轴于点P,连接PC.若△PCD的面积为4,则k的值为( )
A.8 B.12 C.16 D.18
【解答】解:过点B分别作BM⊥AD于点M,BN⊥CD于点N,
设点B(a,b),k=ab,
则BN∥AD,则△CNB∽△CDA,
则,即,
∴ADb,
则k=abb xA,则xAa,
则点A(a,b),则点D(a,0),
由点B、D的坐标得,直线BD的表达式为:yxb,
则点P(0,b);
由点A、B的坐标得,直线AB的表达式为:yb,
则点C(,0)则CD=a,
∵S△PCDCD OPa b=4,
则ab=12=k,
故选:B.
6.(2025春 姑苏区校级期中)如图,点A在反比例函数图象上,过A作AC⊥x轴,垂足为C,且OC=6,OA的垂直平分线交OC于B,则△ABC的周长为( )
A.7 B.8 C. D.
【解答】解:∵点A在反比例函数图象上,
∴S△AOC3,
∵3,OC=6,
∴AC=1,
∵OA的垂直平分线交OC于B,
∴AB=OB,
∴△ABC的周长=OC+AC=6+1=7.
故选:A.
7.(2025 江阴市二模)反比例函数(k为常数)的图象上有P(t,y1),Q(t+2,y2)两点.下列选项正确的是( )
A.当t<﹣2时,y2<y1<0 B.当t>0时,y1<y2<0
C.当﹣2<t<0时,0<y1<y2 D.当﹣2<t<0时,y1<0<y2
【解答】解:根据反比例函数的图象和性质逐项分析判断如下:
由条件可知﹣(k2+1)<0,
∴的图象在第二、第四象限内,在每个象限,y随x增大而增大,
当t<﹣2时,则t+2<0,
∴P(t,y1),Q(t+2,y2)都在第二象限,
∴0<y1<y2,故A选项错误,不符合题意;
当t>0时,则t+2>0,
∴P(t,y1),Q(t+2,y2)都在第四象限,
∴y1<y2<0,故B选项正确,符合题意;
当﹣2<t<0时,t+2>0,P(t,y1)在第二象限,Q(t+2,y2)在第四象限,
∴y1>0>y2,故C选项错误,不符合题意;D选项错误,不符合题意;
故选:B.
8.(2024春 亭湖区月考)如图,点A在反比例函数的图象上,点B在反比例函数的图象上,AB∥y轴,交x轴于点C,连结OA,取OA的中点D,连结BD,则△ADB(阴影部分)的面积为( )
A.16 B.8 C.4 D.2
【解答】解:∵点A在反比例函数的图象上,
∴S△AOC,
∵点B在反比例函数的图象上,
∴S△BOC2,
∴S△AOB=S△AOC﹣S△BOC=6﹣2=4,
∵D是OA的中点,
∴S阴影S△AOB2.
故选:D.
二.填空题(共7小题)
9.(2025 新吴区二模)已知一个函数的图象在第一象限内y随着x的增大而增大,请写出符合条件的函数表达式 y=x(答案不唯一) .
【解答】解:∵一个函数的图象在第一象限内y随着x的增大而增大,
∴函数关系式可以是:y=x或y=x2(答案不唯一).
故答案为:y=x(答案不唯一).
10.(2025 惠山区二模)在平面直角坐标系中,某函数的图象经过点(﹣2,1).且函数y随自变量x的增大而减小,请写出一个符合要求的函数表达式 y=﹣x﹣1(答案不唯一) .
【解答】解:由题意得k<0,设y=﹣x+b,
∵图象经过点(﹣2,1),
∴1=﹣(﹣2)+b,
解得:b=﹣1,
∴函数表达式为y=﹣x﹣1.
故答案为:y=﹣x﹣1(答案不唯一).
11.(2025春 沛县月考)若点A(x1,y1),B(x2,y2)在函数的图象上,且x1<x2<0,则y1 < y2(填“<”或“>”).
【解答】解:∵k=﹣5<0,
∴反比例函数的图象在第二、四象限,
∴在每一个象限内y随x的增大而增大,
∵x1<x2<0,
∴y1<y2.
故答案为:<.
12.(2025 盐城二模)如图,在平面直角坐标系中,四边形OCBA为菱形,点A落在反比例函数y(x>0)上,且tan∠AOC,点B落在反比例函数y(x>0)上,则k= 32 .
【解答】解:过点A、B作x轴的垂线,垂足分别为D、E,
∵tan∠AOC,
∴,
∴设AD=4a,则OD=3a,
∴点A(3a,4a),
由题意可得:3a 4a=12,
∴a=1(负值已舍),
∴点A(3,4),
∴AD=4,OD=3,
∴OA5,
∵,AB∥CO,
∴点B(8,4),
∵点B落在反比例函数y(x>0)上,
∴k=8×4=32,
故答案为:32.
13.(2025 扬州二模)如图,平面直角坐标系xOy中,函数的图象经过A(x1,y1),B(x2,y2)两点.若△ABO的面积为,则的值为 .
【解答】解:如图,作AD⊥x轴,BC⊥x轴,垂足分别为D、C,
根据反比例函数k值的几何意义可得:
S△AOB=S梯形ABCD,
∴(y1+y2)(x2﹣x1),
整理得:x2y1﹣x1y2=9,
∵x1y1 x2y2=36,
∴x1y2 x2y1=36,
∴(x2y1﹣9)x2y1=36,
解得x2y1=12,
∴.
故答案为:.
14.(2025春 苏州期中)如图,平面直角坐标系中,点A(2,6)为反比例函数的图象一点,点B为x轴上一点,连接AB,过点A作AC⊥AB,交反比例函数的图象于点C,连接BC,若△ABC为等腰直角三角形,则点B的横坐标为 .
【解答】解:作AM⊥x轴于M,CD⊥x轴于D,CN⊥AM于N,
∵A(2,6),
∴OM=2,AM=6,
∵点A(2,6)为反比例函数的图象一点,
∴k=2×6=12,
∴反比例函数为y,
设C(a,),则OD=a,CD,
∵AC⊥AB,
∴∠BAM+∠CAN=90°,
∵∠ABM+∠BAM=90°,
∴∠ABM=∠CAN,
∵∠AMB=∠CNA=90°,AB=AC,
∴△AMB≌△CAN(AAS),
∴BM=AN=6,CN=AM=6,
∴OD=OM+MD=OD+CN,
∴a=2+6=8,
∴BM=6,
∴OB=BM﹣OM2,
∴B点的横坐标为,
故答案为:.
15.(2025春 雨花台区校级月考)验光师通过检测发现近视眼镜的度数y(度)与镜片焦距x(米)成反比例,y关于x的函数图象如图所示.经过一段时间的矫正治疗后,小雪的镜片焦距由0.25米调整到0.5米,则近视眼镜的度数减少了 200 度.
【解答】解:设y(k≠0),
把(0.2,500)代入y(k≠0),
∴k=500×0.2=100,
∴函数解析式为y,
当x=0.25时,y400,
当x=0.5时,y200,
∴度数减少了400﹣200=200(度),
故答案为:200.
三.解答题(共6小题)
16.(2025春 苏州期中)如图,一次函数y=kx+b(k,b是常数,k≠0)的图象与反比例函数(m是常数,m≠0)的图象交于点A(n,1),B(﹣2,﹣2),x轴上一点M(﹣4,0),连接AM,BM.
(1)求一次函数与反比例函数的表达式;
(2)求△ABM的面积.
【解答】解:(1)∵两个函数图象交于点A(n,1),B(﹣2,﹣2),
∴m=﹣2×(﹣2)=4,
∴反比例函数解析式为y,
∵点A(4,1)和B(﹣2,﹣2)在一次函数y=kx+b(k,b是常数,k≠0)的图象上,
,解得,
∴一次函数解析式为y1.
(2)如图,直线AB交x轴于点C,
在直线y1中,当y=0时,x=2,
∴C(2,0),
∴CM=6,
∴S△ABM=S△AMC+S△BMC9.
17.(2025春 亭湖区校级期中)如图,在平面直角坐标系中,双曲线y经过点A(6,1),过点A作AB⊥y轴,垂足为点B,点C是双曲线第三象限上一点,连接AC,BC.
(1)求k的值;
(2)若△ABC的面积为12,求直线AC的解析式
【解答】解:(1)∵双曲线y,经过点A(6,1),
∴1,
解得k=6;
(2)设点C到AB的距离为h,
∵点A的坐标为(6,1),AB⊥y轴,
∴AB=6,
∴S△ABC6 h=12,
解得h=4,
∵点A的纵坐标为1,
∴点C的纵坐标为1﹣4=﹣3,
∴3,
解得x=﹣2,
∴点C的坐标为(﹣2,﹣3),
设直线AC的解析式为y=kx+b,
则,解得,
所以,直线AC的解析式为yx﹣2.
18.(2025 淮阴区模拟)如图,四边形ABCD为正方形,点A的坐标为(0,2),点B的坐标为(0,﹣3),反比例函数的图象经过点C,一次函数y=ax+b(a≠0)的图象经过点C和点A.
(1)求反比例函数与一次函数的表达式;
(2)点P是反比例函数图象上的一点,若△OAP的面积恰好等于正方形ABCD的面积的,求点P坐标.
【解答】(1)解:∵A(0,2),B(0,﹣3),
∴BC=AB=5,
∴C(5,﹣3),
把C(5,﹣3)代入y得:﹣3,
∴k=﹣3×5=﹣15,
∴反比例函数解析式为y;
把A(0,2),C(5,﹣3)代入一次函数y=ax+b得:
,
解得,
∴一次函数解析式为y=﹣x+2;
(2)设P点的坐标为(x,y),
∵S△OAPS正方形ABCD,
∴丨x丨=25,
解得:x=±15,
当x=15时,y=﹣1;
当x=﹣15时;y=1
∴P(15,﹣1)或(﹣15,1).
19.(2025春 兴化市期中)反比例函数的图象经过点A(1,2a)和点B(5﹣a,3).
(1)求a、k的值;
(2)如图①,在反比例函数的图象上有一点P,小明发现将点P绕原点O顺时针方向旋转90°后得到的点Q在另一个反比例函数图象上,求出点Q所在的函数表达式,并写出自变量取值范围;
(3)如图②,已知直线l1:y=x和l2:y=﹣x,将反比例函数的图象绕原点旋转45°后得到新图象,在新图象上任取一点Q,过点Q作QM⊥l1,QN⊥l2,垂足分别为点M,点N.求四边形QMON的面积.
【解答】解:(1)将点A、B的坐标代入反比例函数表达式得:k=2a=3(5﹣a),
则a=3,k=6;
(2)设点P(m,n),则mn=6,则点Q(n,﹣m),
则﹣mn=﹣6,
则点Q所在的函数表达式为y(x>0);
(3)将直线l1:y=x、l2:y=﹣x,反比例函数的图象绕原点逆时针旋转45°,
则OM、ON、反比例函数分别和y轴、x轴、原反比例函数重合,
则四边形QMON的面积=k=6.
20.(2025 苏州一模)如图,已知一次函数的图象与反比例函数的图象相交于点A,点B(点A在点B的左侧).连接OA,过点B作BD⊥y轴,垂足为D,与OA交于点C.
(1)当点B的坐标为(6,n)时,求k的值;
(2)当时,求线段OD的长.
【解答】解:(1)把点B的坐标为(6,n)代入得n4=1,
∴B(6,1),
把B(6,1)代入得1,
∴k=6;
(2)过B作BH⊥x轴于H,
∵BD⊥y轴,
∴∠BDO=∠DOH=∠BHO=90°,
∴四边形BDOH是矩形,
∴OD=BH,
过A作AE⊥y轴于E,
∴CD∥AE,
∴△OCD∽△OAE,
∴,
∵,
∴,
解得,,
∴B(4,),A(4,),
∴OD,OE,
∵OE=4OD,
∴4,
∴k,
∴OD.
21.(2024春 鼓楼区校级期末)如图,已知正比例函数的图象与反比例函数的图象相交于点A(3,n)和点 B.
(1)求反比例函数的解析式;
(2)请结合函数图象,直接写出不等式的解集;
(3)如图,以AO为边作菱形AOCD,使点C在x轴正半轴上,点D在第一象限,双曲线交CD于点E,连接AE、OE,求△AOE的面积.
【解答】解:(1)把点A(3,n)代入正比例函数可得:n=4,
∴点A(3,4),
把点A(3,4)代入反比例函数,
可得:k=3×4=12,
∴反比例函数的解析式为;
(2)∵点A与点B是关于原点对称的,
∴点B(﹣3,﹣4),
∴根据图象可得,不等式的解集为:x<﹣3或0<x<3;
(3)如图所示,过点A作AG⊥x轴,垂足为G,
∵A(3,4),
∴OG=3,AG=4,
在Rt△AOG中,,
∵四边形AOCD是菱形,
∴OC=OA=5,,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
