【江苏省各地区真题汇编】空间向量与立体几何考前专题特训-2025年高考数学(含解析)
文档属性
| 名称 | 【江苏省各地区真题汇编】空间向量与立体几何考前专题特训-2025年高考数学(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-26 21:20:39 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【江苏省各地区真题汇编】空间向量与立体几何考前专题特训-2025年高考数学
一.选择题(共8小题)
1.(2025春 江苏校级期中)若,,则( )
A.(2,0,﹣3) B.(2,﹣1,1) C.(﹣2,1,﹣1) D.(2,1,﹣3)
2.(2025春 江苏校级期中)在平行六面体ABCD﹣A1B1C1D1中∠BAD=90°,AB=AD=AA1=1,∠BAA1=∠DAA1=60°.取棱B1C1的中点M,则( )
A. B. C. D.
3.(2025春 常州期中)如图,直三棱柱ABC﹣A1B1C1中,AB=AC=BC=AA1=2,点P为侧面ABB1A1上的任意一点,则的取值范围是( )
A.[0,2] B.[1,3] C.[2,4] D.[3,5]
4.(2025春 淮安期中)在三棱锥P﹣ABC中,,,,且,,则( )
A. B.
C. D.
5.(2025春 江苏校级期中)已知平面α的法向量为,平面β的法向量为,若α∥β,则xy=( )
A.﹣1 B.1 C. D.
6.(2025春 溧阳市期中)已知动点P是棱长为1的正方体ABCD﹣A1B1C1D1的对角线BD1上一点,记,当∠APC为钝角时,λ的取值范围为( )
A. B. C. D.
7.(2025春 高邮市期中)在空间向量中,我们给出了定义向量的“外积”运算规则:对于空间向量和,.已知,,平面α的法向量,直线l的方向向量,则直线l与平面α的位置关系是( )
A.平行 B.垂直
C.直线l在平面α内 D.相交但不垂直
8.(2025春 淮安期中)关于空间向量,以下说法正确的是( )
A.若对空间中任意一点O,有,则P,A,B,C四点共面
B.若空间向量,满足,则与夹角为锐角
C.若直线l的方向向量为,平面α的一个法向量为,则l∥α
D.若空间向量,则在的投影向量为
二.多选题(共3小题)
(多选)9.(2025春 如皋市月考)在棱长为2的正方体ABCD﹣A1B1C1D1中,P是AC上的动点(包含两端点),则下列结论正确的是( )
A.存在点P,使B1P与平面A1DC1相交
B.B1P⊥BD1
C.D1P与平面AB1C所成角的正弦最大值为
D.A1P+B1P的最小值为
(多选)10.(2024春 锡山区校级期末)在三棱锥D﹣ABC中,平面ABC⊥平面ABD,AB=AC=BC=BD=AD=2,则( )
A.三棱锥D﹣ABC的体积为1
B.点C到直线AD的距离为
C.二面角B﹣AD﹣C的正切值为2
D.三棱锥D﹣ABC外接球的球心到平面ABD的距离为
(多选)11.(2023秋 苏州期末)如图,在长方体ABCD﹣A1B1C1D1中,已知AB=2,BC,AA1=1,P为棱C1D1的中点,Q为底面ABCD上(含边界)的一动点.记点Q轨迹的长度为L,则下列说法正确的有( )
A.若PQ⊥B1C,则L=2
B.若PQ∥平面A1BC1,则L
C.若PQ,则L=π
D.若C到平面A1PQ的距离为,则L=2
三.填空题(共3小题)
12.(2025春 常州期中)已知向量的夹角为钝角,则实数t的取值范围为 .
13.(2025春 淮安期中)《九章算术》是我国古代数学名著,它在几何学中的研究比西方早一千多年,书中将四个面均为直角三角形的四面体称为鳖臑.如图,四面体P﹣ABC为鳖臑,PA⊥平面ABC,AB⊥BC,且PA=AB=BC=1,则直线PB与平面PAC所成角的大小为 .
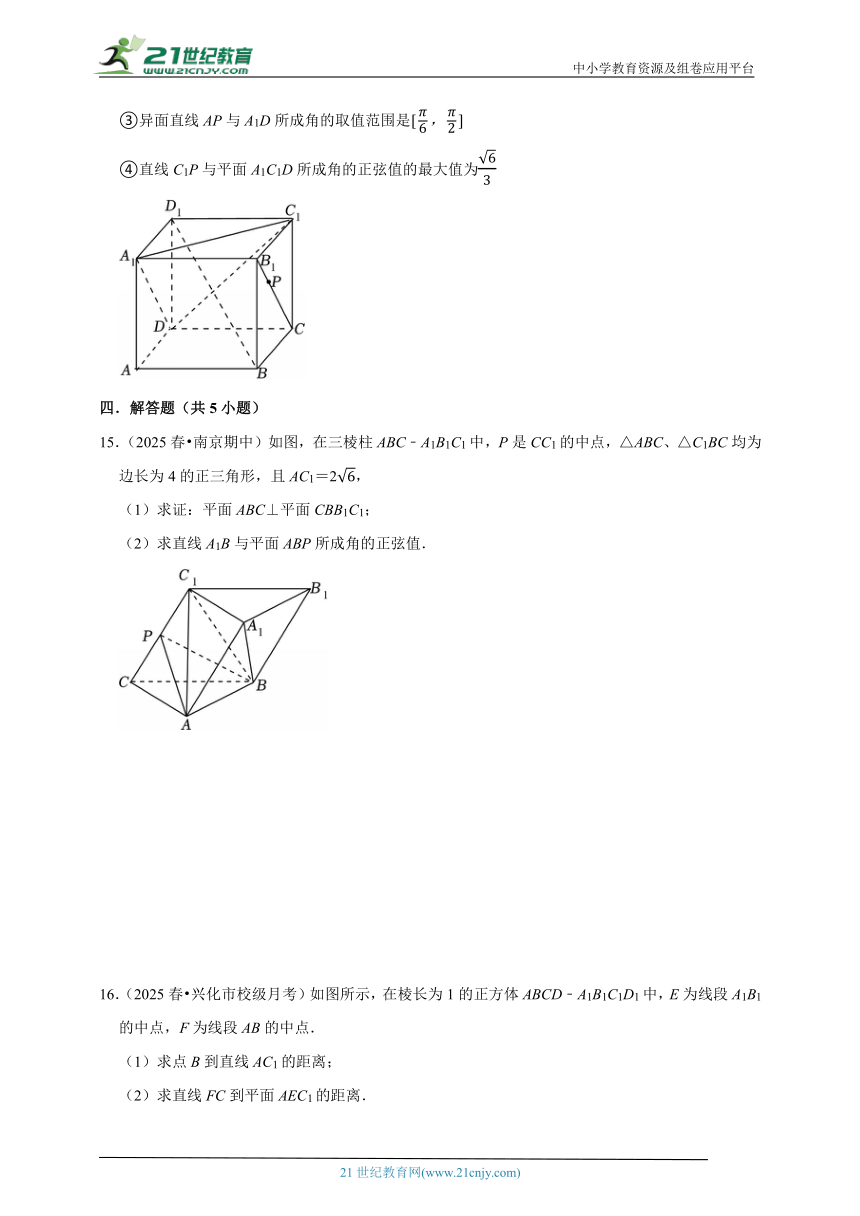
14.(2025春 邗江区校级期中)如图,在正方体ABCD﹣A1B1C1D1中,点P在线段B1C上运动,则下列结论正确的是 .
①直线BD1⊥平面A1C1D
②三棱锥D﹣A1C1P的体积为定值
③异面直线AP与A1D所成角的取值范围是
④直线C1P与平面A1C1D所成角的正弦值的最大值为
四.解答题(共5小题)
15.(2025春 南京期中)如图,在三棱柱ABC﹣A1B1C1中,P是CC1的中点,△ABC、△C1BC均为边长为4的正三角形,且AC1=2,
(1)求证:平面ABC⊥平面CBB1C1;
(2)求直线A1B与平面ABP所成角的正弦值.
16.(2025春 兴化市校级月考)如图所示,在棱长为1的正方体ABCD﹣A1B1C1D1中,E为线段A1B1的中点,F为线段AB的中点.
(1)求点B到直线AC1的距离;
(2)求直线FC到平面AEC1的距离.
17.(2025 鼓楼区校级模拟)如图,在直四棱柱ABCD﹣A1B1C1D1中,AD=2,BC=CD,∠DCB=90°,∠DAB=45°,E,F分别为AD,AB的中点.
(1)求证:AD⊥BD;
(2)求证:平面BDC1∥平面EFD1;
(3)若CC1=2,P是线段D1F上的动点,求直线A1P与平面BDC1所成角的正弦值的最大值.
18.(2025春 盐城月考)如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,E为AD的中点,PA⊥AD,BE∥CD,BE⊥AD,PA=AE=BE=2,CD=1.
(1)求A到平面PBC的距离;
(2)求直线PE与平面PBC所成角的正弦值;
(3)在线段PE上是否存在点M,使得DM∥平面PBC?若存在,求出点M的位置;若不存在,说明理由.
19.(2025春 江苏校级期中)如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,且∠ABC=60°,PA⊥平面ABCD,PA=AB=2,点E,F为PC,PA的中点.
(1)求证:平面BDE⊥平面ABCD;
(2)二面角E﹣BD﹣F的大小;
(3)线段PC上是否存在点M,使得直线AM与平面BDF所成夹角为.若存在,求出M点的位置;若不存在,请说明理由.
【江苏省各地区真题汇编】空间向量与立体几何考前专题特训-2025年高考数学
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D B C D A C D A
二.多选题(共3小题)
题号 9 10 11
答案 BCD ACD ACD
一.选择题(共8小题)
1.(2025春 江苏校级期中)若,,则( )
A.(2,0,﹣3) B.(2,﹣1,1) C.(﹣2,1,﹣1) D.(2,1,﹣3)
【解答】解:由题可得:.
故选:D.
2.(2025春 江苏校级期中)在平行六面体ABCD﹣A1B1C1D1中∠BAD=90°,AB=AD=AA1=1,∠BAA1=∠DAA1=60°.取棱B1C1的中点M,则( )
A. B. C. D.
【解答】解:平行六面体ABCD﹣A1B1C1D1中∠BAD=90°,AB=AD=AA1=1,∠BAA1=∠DAA1=60°,取棱B1C1的中点M,
根据向量的线性运算,则
所以,
所以.
故选:B.
3.(2025春 常州期中)如图,直三棱柱ABC﹣A1B1C1中,AB=AC=BC=AA1=2,点P为侧面ABB1A1上的任意一点,则的取值范围是( )
A.[0,2] B.[1,3] C.[2,4] D.[3,5]
【解答】解:直三棱柱ABC﹣A1B1C1中,AB=AC=BC=AA1=2,点P为侧面ABB1A1上的任意一点,
如图取AB中点为原点O,建立空间直角坐标系,设P(x,0,z),
其中﹣1≤x≤1,0≤z≤2,,,
,,,
当x=±1,且z=0或z=2时,取最大值4,
当x=0,且z=1时,取最小值2,所以的取值范围为[2,4].
故选:C.
4.(2025春 淮安期中)在三棱锥P﹣ABC中,,,,且,,则( )
A. B.
C. D.
【解答】解:如图所示,连接BM,因为,,则,,
所以.
故选:D.
5.(2025春 江苏校级期中)已知平面α的法向量为,平面β的法向量为,若α∥β,则xy=( )
A.﹣1 B.1 C. D.
【解答】解:根据题意,平面α的法向量为,平面β的法向量为,
若α∥β,则有,即,解可得x=4,,
故xy=﹣1.
故选:A.
6.(2025春 溧阳市期中)已知动点P是棱长为1的正方体ABCD﹣A1B1C1D1的对角线BD1上一点,记,当∠APC为钝角时,λ的取值范围为( )
A. B. C. D.
【解答】解:由题设,建立如图所示空间直角坐标系:
则有A(1,0,0),B(1,1,0),C(0,1,0),D1(0,0,1),
∴
∴,
,
显然∠APC不是平角,
所以∠APC为钝角等价于cos∠APC<0,即,
∴(λ﹣1)λ+λ(λ﹣1)+λ2=λ(3λ﹣2)<0,
解得,
则λ的取值范围是.
故选:C.
7.(2025春 高邮市期中)在空间向量中,我们给出了定义向量的“外积”运算规则:对于空间向量和,.已知,,平面α的法向量,直线l的方向向量,则直线l与平面α的位置关系是( )
A.平行 B.垂直
C.直线l在平面α内 D.相交但不垂直
【解答】解:因为,,
所以平面α的法向量为,
因为直线l的方向向量,所以,所以与不垂直.
因为,所以与不平行,
所以与既不垂直也不平行,所以直线l与平面α相交但不垂直.
故选:D.
8.(2025春 淮安期中)关于空间向量,以下说法正确的是( )
A.若对空间中任意一点O,有,则P,A,B,C四点共面
B.若空间向量,满足,则与夹角为锐角
C.若直线l的方向向量为,平面α的一个法向量为,则l∥α
D.若空间向量,则在的投影向量为
【解答】解:A选项,根据题意可知,中,故P,A,B,C四点共面,A选项正确;
B选项,当,同向共线时也成立,但与夹角不为锐角,B选项错误;
C选项,根据题意可知,,即,故l⊥α,C选项错误;
D选项,在上的投影向量为,D选项错误.
故选:A.
二.多选题(共3小题)
(多选)9.(2025春 如皋市月考)在棱长为2的正方体ABCD﹣A1B1C1D1中,P是AC上的动点(包含两端点),则下列结论正确的是( )
A.存在点P,使B1P与平面A1DC1相交
B.B1P⊥BD1
C.D1P与平面AB1C所成角的正弦最大值为
D.A1P+B1P的最小值为
【解答】解:选项A,连接AB1,CB1,则AB1∥C1D,AC∥A1C1,
因为AB1∩AC=A,AB1、AC 平面AB1C,C1D∩A1C1=C1,C1D、A1C1 平面A1DC1,
所以平面AB1C∥平面A1DC1,
由P是AC上的动点(包含两端点),知B1P 平面AB1C,
所以B1P∥平面A1DC1,
所以不存在点P,使B1P与平面A1DC1相交,故选项A错误;
选项B,由三垂线定理的逆定理知,BD1⊥AC,BD1⊥AB1,
因为AC∩AB1=A,AC、AB1 平面AB1C,所以BD1⊥平面AB1C,
又B1P 平面AB1C,所以BD1⊥B1P,故选项B正确;
选项C,由BD1⊥平面AB1C,知∠D1PQ即为D1P与平面AB1C所成角,
要求sin∠D1PQ的最大值,需求tan∠D1PQ,
在Rt△D1PQ中,tan∠D1PQ,
设AC∩BD=O,连接OB1,设OB1∩BD1=Q,连接OQ,
在四边形OBB1D1中,,
所以QD1BD1,
而PQ≥OQOB1,
所以tan∠D1PQ2,此时sin∠D1PQ,
所以D1P与平面AB1C所成角的正弦最大值为,故选项C正确;
选项D,将平面A1AC与平面AB1C展开至同一平面,如图所示,
其中△A1AC为直角三角形,△AB1C为等边三角形,且A1A=2,AB1=2,
连接A1B1,
当点P为A1B1与AC的交点时,A1P+B1P取得最小值A1B1,
在△AA1B1中,由余弦定理知,12+4,
所以A1B12,
即A1P+B1P的最小值为2,故选项D正确.
故选:BCD.
(多选)10.(2024春 锡山区校级期末)在三棱锥D﹣ABC中,平面ABC⊥平面ABD,AB=AC=BC=BD=AD=2,则( )
A.三棱锥D﹣ABC的体积为1
B.点C到直线AD的距离为
C.二面角B﹣AD﹣C的正切值为2
D.三棱锥D﹣ABC外接球的球心到平面ABD的距离为
【解答】解:在三棱锥D﹣ABC中,平面ABC⊥平面ABD,AB=AC=BC=BD=AD=2,
如图,取AB的中点G,连接DG,CG,
∵平面ABC⊥平面ABD,且平面ABC∩平面ABD=AB,CG 平面ABC,∴CG⊥平面ABD,
∵,∴,故A正确;
取AD的中点E,连接BE,取AE的中点F,连接FG,CF,
∵F,G分别为AE,AB中点,∴FG∥BE,∴FG⊥AD,
∵CG⊥平面ABD,AD 平面ABD,∴CG⊥AD,
又CG∩FG=G,CG,FG 平面CFG,∴AD⊥平面CFG,则AD⊥CF,
则点C到直线AD的距离为为二面角B﹣AD﹣C的平面角,
,故B错误,C正确;
设△ABD,△ABC的外心分别为M,K,则GK⊥AB,
又平面ABD⊥平面ABC,∴GK⊥平面ABD.
设三棱锥D﹣ABC外接球的球心为O,则OK⊥平面ABC,OM⊥平面ABD,
∴四边形OMGK为矩形,则,
∴三棱锥D﹣ABC外接球的球心到平面ABD的距离为,故D正确.
故选:ACD.
(多选)11.(2023秋 苏州期末)如图,在长方体ABCD﹣A1B1C1D1中,已知AB=2,BC,AA1=1,P为棱C1D1的中点,Q为底面ABCD上(含边界)的一动点.记点Q轨迹的长度为L,则下列说法正确的有( )
A.若PQ⊥B1C,则L=2
B.若PQ∥平面A1BC1,则L
C.若PQ,则L=π
D.若C到平面A1PQ的距离为,则L=2
【解答】解:对A选项,如图,
设Q在BC上的射影为M,PQ⊥B1C,即C1M⊥B1C,
易得,故L=MN=2,故A选项正确;
对B选项:如图,取AB,BC中点E,F,
显然有PE∥BC1,EF∥A1C1,
进而可得平面PEF∥平面A1BC1,故,故B选项错误;
对C选项:如图,设P在CD上的射影为N,
由PQ,PN=1,易得NQ=1,
故Q在以N为圆心,1为半径的半圆弧上,故L=π,故C选项正确;
对D:以D为原点建系如图,
则,设Q(m,n,0),m∈[0,],n∈[0,2],
所以,,,
设平面A1PQ的法向量为,
则,取,
所以C到平面A1PQ的距离为,
所以,
所以,
即或,
即或,
但当Q(m,n,0)满足时,直线在矩形ABCD外,
所以L2,故D选项正确.
故选:ACD.
三.填空题(共3小题)
12.(2025春 常州期中)已知向量的夹角为钝角,则实数t的取值范围为 (﹣∞,﹣4)∪(﹣4,5) .
【解答】解:因为向量的夹角为钝角,
则,解得t<5,
当共线时,由,即(﹣4,2,t)=λ(2,﹣1,2),解得t=﹣4,
所以当夹角为钝角时t∈(﹣∞,﹣4)∪(﹣4,5).
故答案为:(﹣∞,﹣4)∪(﹣4,5).
13.(2025春 淮安期中)《九章算术》是我国古代数学名著,它在几何学中的研究比西方早一千多年,书中将四个面均为直角三角形的四面体称为鳖臑.如图,四面体P﹣ABC为鳖臑,PA⊥平面ABC,AB⊥BC,且PA=AB=BC=1,则直线PB与平面PAC所成角的大小为 .
【解答】解:取AC的中点O,连接OB,OP,
因为AB⊥BC,且AB=BC=1,所以OB⊥AC,且OBAC,
因为PA⊥平面ABC,AC、OB 平面ABC,所以PA⊥AC,PA⊥OB,
又AC∩PA=A,AC、PA 平面PAC,所以OB⊥平面PAC,
所以∠OPB即为直线PB与平面PAC所成角,
在Rt△PAO中,PA=1,OA,所以OP,
所以tan∠OPB,
所以∠OPB,
即直线PB与平面PAC所成角的大小为.
故答案为:.
14.(2025春 邗江区校级期中)如图,在正方体ABCD﹣A1B1C1D1中,点P在线段B1C上运动,则下列结论正确的是 ①②④ .
①直线BD1⊥平面A1C1D
②三棱锥D﹣A1C1P的体积为定值
③异面直线AP与A1D所成角的取值范围是
④直线C1P与平面A1C1D所成角的正弦值的最大值为
【解答】解:对①,根据三垂线定理易知BD1⊥A1C1,BD1⊥A1D,从而可得BD1⊥平面A1C1D,∴①正确;
对②,易知B1C∥A1D,从而可得B1C∥平面A1C1D,
∴P到平面A1C1D距离为定值,又△A1C1D的面积也为定值,
∴三棱锥D﹣A1C1P的体积为定值,∴②正确;
对③,∵B1C∥A1D,
∴异面直线AP与A1D所成角即为相交直线AP与B1C所成角,
又易知△AB1C为等边三角形,
∴相交直线AP与B1C所成角的范围为[,],
即异面直线AP与A1D所成角的取值范围是[,],∴③错误;
对④,由①知BD1⊥平面A1C1D,
∴直线C1P与平面A1C1D所成角的正弦值为:
C1P与BD1所成角的余弦值,
如图将C1P对称平移至D1Q,
则C1P与BD1所成角的余弦值即为:
D1Q与BD1所成角的余弦值,其中Q为线段A1D上的动点,
又AB⊥平面ADD1A1,∴AB⊥D1Q,
∴当Q为A1D的中点时,D1Q与BD1所成角的余弦值最大,
最大值为,
∴直线C1P与平面A1C1D所成角的正弦值的最大值为,∴④正确.
故答案为:①②④.
四.解答题(共5小题)
15.(2025春 南京期中)如图,在三棱柱ABC﹣A1B1C1中,P是CC1的中点,△ABC、△C1BC均为边长为4的正三角形,且AC1=2,
(1)求证:平面ABC⊥平面CBB1C1;
(2)求直线A1B与平面ABP所成角的正弦值.
【解答】解:(1)证明:如图,取BC的中点O,连接AO,C1O,
因为△ABC、△C1BC均为边长为4的正三角形,
所以AO⊥CB,C1O⊥CB,A1O=C1O=2,△C1AO中,AO2,
所以AO⊥C1O,
又AO∩C1O=O,BC,C1O 平面CBB1C1,所以AO⊥平面CBB1C1,
又因为AO 平面ABC,
所以平面ABC⊥平面CBB1C1;
(2)以直线OA,OB,OC1所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,
则A(2,0,0),B(0,2,0),C(0,﹣2,0),C1(0,0,2),B1(0,4,2),P(0,﹣1,),
由,得,,,,
设(x,y,z)是平面PAB的一个法向量,
则,
令,则,
设直线A1B与平面ABP所成角为θ,
则sinθ=|cos,|,
所以直线A1B与平面ABP所成角的正弦值为.
16.(2025春 兴化市校级月考)如图所示,在棱长为1的正方体ABCD﹣A1B1C1D1中,E为线段A1B1的中点,F为线段AB的中点.
(1)求点B到直线AC1的距离;
(2)求直线FC到平面AEC1的距离.
【解答】解:(1)以D1为坐标原点,分别以D1A1,D1C1,D1D所在直线为x,y,z轴建立空间直角坐标系,
则A(1,0,1),B(1,1,1),C(0,1,1),C1(0,1,0),E(1,,0),F(1,,1),
∴,,,,
,,
(1)取,,
,,则点B到直线AC1的距离为;
(2)∵,∴FC∥EC1,
而FC 平面AEC1,EC1 平面AEC1,∴FC∥平面AEC1,
则点F到平面AEC1的距离就是直线FC到平面AEC1的距离.
设平面AEC1的一个法向量为,
由,取y=2,得,
又,
∴直线FC到平面AEC1的距离为.
17.(2025 鼓楼区校级模拟)如图,在直四棱柱ABCD﹣A1B1C1D1中,AD=2,BC=CD,∠DCB=90°,∠DAB=45°,E,F分别为AD,AB的中点.
(1)求证:AD⊥BD;
(2)求证:平面BDC1∥平面EFD1;
(3)若CC1=2,P是线段D1F上的动点,求直线A1P与平面BDC1所成角的正弦值的最大值.
【解答】解:(1)证明:在直四棱柱ABCD﹣A1B1C1D1中,AD=2,BC=CD,
∠DCB=90°,∠DAB=45°,E,F分别为AD,AB的中点,
∵DC=BC,∠DCB=90°,
∴BD2,又AD=2,∴BD=AD=2,
又∠DAB=45°,∴∠ABD=45°,∴∠ADB=90°,∴AD⊥BD.
(2)证明:在直四棱柱ABCD﹣A1B1C1D1中,DD1⊥平面ABCD,
∵AD 平面ABCD,BD 平面ABCD,∴DD1⊥AD,DD1⊥BD,
∴DA,DB,DD1两两垂直,
以点D为坐标原点,以DA所在直线为x轴,DB所在直线为y轴,DD1所在直线为z轴,建立空间直角坐标系,如图,
设DD1=h(h>0),
则D(0,0,0),B(0,2,0),C1(﹣1,1,h),E(1,0,0),F(1,1,0),D1(0,0,h).
∴(0,2,0),(﹣1,1,h),(0,1,0),(﹣1,0,h),
设为平面BDC1的法向量,
则,令x1=h,得(h,0,1),
设平面EFD1的法向量,
则,取x=h,得(h,0,1),
∵∥,平面BDC1与平面EFD1不重合,
∴平面BDC1∥平面EFD1.
(3)CC1=2,P是线段D1F上的动点,
当CC1=2时,为平面BDC1的法向量,
D1(0,0,2),则(﹣1,﹣1,2),
设λ(﹣1,﹣1,2)=(﹣λ,﹣λ,2λ),(λ∈[0,1]),
∴P(1﹣λ,1﹣λ,2λ),∵A1(2,0,2),∴(﹣1﹣λ,1﹣λ,2λ﹣2),
设直线A1P与平面BDC1所成角为θ,
sinθ=|cos|
,
当且仅当时,等号成立,
∴若CC1=2,P是线段D1F上的动点,则直线A1P与平面BDC1所成角的正弦值的最大值为.
18.(2025春 盐城月考)如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,E为AD的中点,PA⊥AD,BE∥CD,BE⊥AD,PA=AE=BE=2,CD=1.
(1)求A到平面PBC的距离;
(2)求直线PE与平面PBC所成角的正弦值;
(3)在线段PE上是否存在点M,使得DM∥平面PBC?若存在,求出点M的位置;若不存在,说明理由.
【解答】解:(1)因为平面PAD⊥平面ABCD,BE⊥AD,平面PAD∩平面ABCD=AD,
所以BE⊥平面PAD,
作Ez⊥AD,以E为原点,以,的方向分别为x轴,y轴的正方向,建立如图所示的空间直角坐标系E﹣xyz,
则点E(0,0,0),P(0,﹣2,2),A(0,﹣2,0),B(2,0,0),C(1,2,0),
D(0,2,0),
所以,,,
设平面PBC的法向量为,
则,所以,即,
取y=1,解得,
A到平面PBC的距离为;
(2)由(1)知,平面PBC的法向量为,
设直线PE与平面PBC所成角为θ,
则直线PE与平面PBC所成角的正弦值为:
,,
所以直线PE与平面PBC所成角的正弦值为;
(3)“线段PE上存在点M,使得DM∥平面PBC”等价于“”,
因为,
设,λ∈[0,1],
则M(0,2λ﹣2,2﹣2λ),.
由(2)知平面PBC的法向量为,
所以,
解得,
所以线段PE上存在点M,即PE中点,使得DM∥平面PBC.
19.(2025春 江苏校级期中)如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,且∠ABC=60°,PA⊥平面ABCD,PA=AB=2,点E,F为PC,PA的中点.
(1)求证:平面BDE⊥平面ABCD;
(2)二面角E﹣BD﹣F的大小;
(3)线段PC上是否存在点M,使得直线AM与平面BDF所成夹角为.若存在,求出M点的位置;若不存在,请说明理由.
【解答】解:(1)证明:连接AC与BD交于点O,连接EO,
∵底面ABCD为菱形,∴点O为AC的中点,
∵点E为PC的中点∴EO∥PA,
又∵PA⊥平面ABCD,∴EO⊥平面ABCD,
又∵EO 平面BDE,
∴平面BDE⊥平面ABCD.
(2)∵EO⊥平面ABCD,且底面ABCD为菱形,∴OB,OC,OE两两垂直.
以O为原点,以向量方向为x,y,z轴正方向建立如图所示空间直角坐标系,
∵底面ABCD为菱形,且∠ABC=60°,则△ABC为等边三角形,
PA=AB=2,∴,
∵O,E分别为AC,PC的中点,∴,
则,
则,
设平面BFD的一个法向量为,
则,有,
令y=1,则,
∵底面ABCD为菱形,∴OC⊥BD,
∵平面BDE⊥平面ABCD,且平面BDE∩平面ABCD=BD,OC 平面ABCD,
∴OC⊥平面BDE,
∴为平面BDE的一个法向量,
设二面角E﹣BD﹣F大小为θ,
则.
∴二面角E﹣BD﹣F的大小为;
(3)不存在,理由如下:
∵点M在线段PC上,设,
由P(0,﹣1,2),C(0,1,0),A(0,﹣1,0)可得,
则,则M(0,2λ﹣1,2﹣2λ),则,
由题意,若直线AM与平面BDF所成夹角为,
则,
整理得2λ2﹣2λ﹣1=0,解出.
又∵0≤λ≤1,∴不符合题意,故线段PC上不存在这样的点M.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【江苏省各地区真题汇编】空间向量与立体几何考前专题特训-2025年高考数学
一.选择题(共8小题)
1.(2025春 江苏校级期中)若,,则( )
A.(2,0,﹣3) B.(2,﹣1,1) C.(﹣2,1,﹣1) D.(2,1,﹣3)
2.(2025春 江苏校级期中)在平行六面体ABCD﹣A1B1C1D1中∠BAD=90°,AB=AD=AA1=1,∠BAA1=∠DAA1=60°.取棱B1C1的中点M,则( )
A. B. C. D.
3.(2025春 常州期中)如图,直三棱柱ABC﹣A1B1C1中,AB=AC=BC=AA1=2,点P为侧面ABB1A1上的任意一点,则的取值范围是( )
A.[0,2] B.[1,3] C.[2,4] D.[3,5]
4.(2025春 淮安期中)在三棱锥P﹣ABC中,,,,且,,则( )
A. B.
C. D.
5.(2025春 江苏校级期中)已知平面α的法向量为,平面β的法向量为,若α∥β,则xy=( )
A.﹣1 B.1 C. D.
6.(2025春 溧阳市期中)已知动点P是棱长为1的正方体ABCD﹣A1B1C1D1的对角线BD1上一点,记,当∠APC为钝角时,λ的取值范围为( )
A. B. C. D.
7.(2025春 高邮市期中)在空间向量中,我们给出了定义向量的“外积”运算规则:对于空间向量和,.已知,,平面α的法向量,直线l的方向向量,则直线l与平面α的位置关系是( )
A.平行 B.垂直
C.直线l在平面α内 D.相交但不垂直
8.(2025春 淮安期中)关于空间向量,以下说法正确的是( )
A.若对空间中任意一点O,有,则P,A,B,C四点共面
B.若空间向量,满足,则与夹角为锐角
C.若直线l的方向向量为,平面α的一个法向量为,则l∥α
D.若空间向量,则在的投影向量为
二.多选题(共3小题)
(多选)9.(2025春 如皋市月考)在棱长为2的正方体ABCD﹣A1B1C1D1中,P是AC上的动点(包含两端点),则下列结论正确的是( )
A.存在点P,使B1P与平面A1DC1相交
B.B1P⊥BD1
C.D1P与平面AB1C所成角的正弦最大值为
D.A1P+B1P的最小值为
(多选)10.(2024春 锡山区校级期末)在三棱锥D﹣ABC中,平面ABC⊥平面ABD,AB=AC=BC=BD=AD=2,则( )
A.三棱锥D﹣ABC的体积为1
B.点C到直线AD的距离为
C.二面角B﹣AD﹣C的正切值为2
D.三棱锥D﹣ABC外接球的球心到平面ABD的距离为
(多选)11.(2023秋 苏州期末)如图,在长方体ABCD﹣A1B1C1D1中,已知AB=2,BC,AA1=1,P为棱C1D1的中点,Q为底面ABCD上(含边界)的一动点.记点Q轨迹的长度为L,则下列说法正确的有( )
A.若PQ⊥B1C,则L=2
B.若PQ∥平面A1BC1,则L
C.若PQ,则L=π
D.若C到平面A1PQ的距离为,则L=2
三.填空题(共3小题)
12.(2025春 常州期中)已知向量的夹角为钝角,则实数t的取值范围为 .
13.(2025春 淮安期中)《九章算术》是我国古代数学名著,它在几何学中的研究比西方早一千多年,书中将四个面均为直角三角形的四面体称为鳖臑.如图,四面体P﹣ABC为鳖臑,PA⊥平面ABC,AB⊥BC,且PA=AB=BC=1,则直线PB与平面PAC所成角的大小为 .
14.(2025春 邗江区校级期中)如图,在正方体ABCD﹣A1B1C1D1中,点P在线段B1C上运动,则下列结论正确的是 .
①直线BD1⊥平面A1C1D
②三棱锥D﹣A1C1P的体积为定值
③异面直线AP与A1D所成角的取值范围是
④直线C1P与平面A1C1D所成角的正弦值的最大值为
四.解答题(共5小题)
15.(2025春 南京期中)如图,在三棱柱ABC﹣A1B1C1中,P是CC1的中点,△ABC、△C1BC均为边长为4的正三角形,且AC1=2,
(1)求证:平面ABC⊥平面CBB1C1;
(2)求直线A1B与平面ABP所成角的正弦值.
16.(2025春 兴化市校级月考)如图所示,在棱长为1的正方体ABCD﹣A1B1C1D1中,E为线段A1B1的中点,F为线段AB的中点.
(1)求点B到直线AC1的距离;
(2)求直线FC到平面AEC1的距离.
17.(2025 鼓楼区校级模拟)如图,在直四棱柱ABCD﹣A1B1C1D1中,AD=2,BC=CD,∠DCB=90°,∠DAB=45°,E,F分别为AD,AB的中点.
(1)求证:AD⊥BD;
(2)求证:平面BDC1∥平面EFD1;
(3)若CC1=2,P是线段D1F上的动点,求直线A1P与平面BDC1所成角的正弦值的最大值.
18.(2025春 盐城月考)如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,E为AD的中点,PA⊥AD,BE∥CD,BE⊥AD,PA=AE=BE=2,CD=1.
(1)求A到平面PBC的距离;
(2)求直线PE与平面PBC所成角的正弦值;
(3)在线段PE上是否存在点M,使得DM∥平面PBC?若存在,求出点M的位置;若不存在,说明理由.
19.(2025春 江苏校级期中)如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,且∠ABC=60°,PA⊥平面ABCD,PA=AB=2,点E,F为PC,PA的中点.
(1)求证:平面BDE⊥平面ABCD;
(2)二面角E﹣BD﹣F的大小;
(3)线段PC上是否存在点M,使得直线AM与平面BDF所成夹角为.若存在,求出M点的位置;若不存在,请说明理由.
【江苏省各地区真题汇编】空间向量与立体几何考前专题特训-2025年高考数学
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D B C D A C D A
二.多选题(共3小题)
题号 9 10 11
答案 BCD ACD ACD
一.选择题(共8小题)
1.(2025春 江苏校级期中)若,,则( )
A.(2,0,﹣3) B.(2,﹣1,1) C.(﹣2,1,﹣1) D.(2,1,﹣3)
【解答】解:由题可得:.
故选:D.
2.(2025春 江苏校级期中)在平行六面体ABCD﹣A1B1C1D1中∠BAD=90°,AB=AD=AA1=1,∠BAA1=∠DAA1=60°.取棱B1C1的中点M,则( )
A. B. C. D.
【解答】解:平行六面体ABCD﹣A1B1C1D1中∠BAD=90°,AB=AD=AA1=1,∠BAA1=∠DAA1=60°,取棱B1C1的中点M,
根据向量的线性运算,则
所以,
所以.
故选:B.
3.(2025春 常州期中)如图,直三棱柱ABC﹣A1B1C1中,AB=AC=BC=AA1=2,点P为侧面ABB1A1上的任意一点,则的取值范围是( )
A.[0,2] B.[1,3] C.[2,4] D.[3,5]
【解答】解:直三棱柱ABC﹣A1B1C1中,AB=AC=BC=AA1=2,点P为侧面ABB1A1上的任意一点,
如图取AB中点为原点O,建立空间直角坐标系,设P(x,0,z),
其中﹣1≤x≤1,0≤z≤2,,,
,,,
当x=±1,且z=0或z=2时,取最大值4,
当x=0,且z=1时,取最小值2,所以的取值范围为[2,4].
故选:C.
4.(2025春 淮安期中)在三棱锥P﹣ABC中,,,,且,,则( )
A. B.
C. D.
【解答】解:如图所示,连接BM,因为,,则,,
所以.
故选:D.
5.(2025春 江苏校级期中)已知平面α的法向量为,平面β的法向量为,若α∥β,则xy=( )
A.﹣1 B.1 C. D.
【解答】解:根据题意,平面α的法向量为,平面β的法向量为,
若α∥β,则有,即,解可得x=4,,
故xy=﹣1.
故选:A.
6.(2025春 溧阳市期中)已知动点P是棱长为1的正方体ABCD﹣A1B1C1D1的对角线BD1上一点,记,当∠APC为钝角时,λ的取值范围为( )
A. B. C. D.
【解答】解:由题设,建立如图所示空间直角坐标系:
则有A(1,0,0),B(1,1,0),C(0,1,0),D1(0,0,1),
∴
∴,
,
显然∠APC不是平角,
所以∠APC为钝角等价于cos∠APC<0,即,
∴(λ﹣1)λ+λ(λ﹣1)+λ2=λ(3λ﹣2)<0,
解得,
则λ的取值范围是.
故选:C.
7.(2025春 高邮市期中)在空间向量中,我们给出了定义向量的“外积”运算规则:对于空间向量和,.已知,,平面α的法向量,直线l的方向向量,则直线l与平面α的位置关系是( )
A.平行 B.垂直
C.直线l在平面α内 D.相交但不垂直
【解答】解:因为,,
所以平面α的法向量为,
因为直线l的方向向量,所以,所以与不垂直.
因为,所以与不平行,
所以与既不垂直也不平行,所以直线l与平面α相交但不垂直.
故选:D.
8.(2025春 淮安期中)关于空间向量,以下说法正确的是( )
A.若对空间中任意一点O,有,则P,A,B,C四点共面
B.若空间向量,满足,则与夹角为锐角
C.若直线l的方向向量为,平面α的一个法向量为,则l∥α
D.若空间向量,则在的投影向量为
【解答】解:A选项,根据题意可知,中,故P,A,B,C四点共面,A选项正确;
B选项,当,同向共线时也成立,但与夹角不为锐角,B选项错误;
C选项,根据题意可知,,即,故l⊥α,C选项错误;
D选项,在上的投影向量为,D选项错误.
故选:A.
二.多选题(共3小题)
(多选)9.(2025春 如皋市月考)在棱长为2的正方体ABCD﹣A1B1C1D1中,P是AC上的动点(包含两端点),则下列结论正确的是( )
A.存在点P,使B1P与平面A1DC1相交
B.B1P⊥BD1
C.D1P与平面AB1C所成角的正弦最大值为
D.A1P+B1P的最小值为
【解答】解:选项A,连接AB1,CB1,则AB1∥C1D,AC∥A1C1,
因为AB1∩AC=A,AB1、AC 平面AB1C,C1D∩A1C1=C1,C1D、A1C1 平面A1DC1,
所以平面AB1C∥平面A1DC1,
由P是AC上的动点(包含两端点),知B1P 平面AB1C,
所以B1P∥平面A1DC1,
所以不存在点P,使B1P与平面A1DC1相交,故选项A错误;
选项B,由三垂线定理的逆定理知,BD1⊥AC,BD1⊥AB1,
因为AC∩AB1=A,AC、AB1 平面AB1C,所以BD1⊥平面AB1C,
又B1P 平面AB1C,所以BD1⊥B1P,故选项B正确;
选项C,由BD1⊥平面AB1C,知∠D1PQ即为D1P与平面AB1C所成角,
要求sin∠D1PQ的最大值,需求tan∠D1PQ,
在Rt△D1PQ中,tan∠D1PQ,
设AC∩BD=O,连接OB1,设OB1∩BD1=Q,连接OQ,
在四边形OBB1D1中,,
所以QD1BD1,
而PQ≥OQOB1,
所以tan∠D1PQ2,此时sin∠D1PQ,
所以D1P与平面AB1C所成角的正弦最大值为,故选项C正确;
选项D,将平面A1AC与平面AB1C展开至同一平面,如图所示,
其中△A1AC为直角三角形,△AB1C为等边三角形,且A1A=2,AB1=2,
连接A1B1,
当点P为A1B1与AC的交点时,A1P+B1P取得最小值A1B1,
在△AA1B1中,由余弦定理知,12+4,
所以A1B12,
即A1P+B1P的最小值为2,故选项D正确.
故选:BCD.
(多选)10.(2024春 锡山区校级期末)在三棱锥D﹣ABC中,平面ABC⊥平面ABD,AB=AC=BC=BD=AD=2,则( )
A.三棱锥D﹣ABC的体积为1
B.点C到直线AD的距离为
C.二面角B﹣AD﹣C的正切值为2
D.三棱锥D﹣ABC外接球的球心到平面ABD的距离为
【解答】解:在三棱锥D﹣ABC中,平面ABC⊥平面ABD,AB=AC=BC=BD=AD=2,
如图,取AB的中点G,连接DG,CG,
∵平面ABC⊥平面ABD,且平面ABC∩平面ABD=AB,CG 平面ABC,∴CG⊥平面ABD,
∵,∴,故A正确;
取AD的中点E,连接BE,取AE的中点F,连接FG,CF,
∵F,G分别为AE,AB中点,∴FG∥BE,∴FG⊥AD,
∵CG⊥平面ABD,AD 平面ABD,∴CG⊥AD,
又CG∩FG=G,CG,FG 平面CFG,∴AD⊥平面CFG,则AD⊥CF,
则点C到直线AD的距离为为二面角B﹣AD﹣C的平面角,
,故B错误,C正确;
设△ABD,△ABC的外心分别为M,K,则GK⊥AB,
又平面ABD⊥平面ABC,∴GK⊥平面ABD.
设三棱锥D﹣ABC外接球的球心为O,则OK⊥平面ABC,OM⊥平面ABD,
∴四边形OMGK为矩形,则,
∴三棱锥D﹣ABC外接球的球心到平面ABD的距离为,故D正确.
故选:ACD.
(多选)11.(2023秋 苏州期末)如图,在长方体ABCD﹣A1B1C1D1中,已知AB=2,BC,AA1=1,P为棱C1D1的中点,Q为底面ABCD上(含边界)的一动点.记点Q轨迹的长度为L,则下列说法正确的有( )
A.若PQ⊥B1C,则L=2
B.若PQ∥平面A1BC1,则L
C.若PQ,则L=π
D.若C到平面A1PQ的距离为,则L=2
【解答】解:对A选项,如图,
设Q在BC上的射影为M,PQ⊥B1C,即C1M⊥B1C,
易得,故L=MN=2,故A选项正确;
对B选项:如图,取AB,BC中点E,F,
显然有PE∥BC1,EF∥A1C1,
进而可得平面PEF∥平面A1BC1,故,故B选项错误;
对C选项:如图,设P在CD上的射影为N,
由PQ,PN=1,易得NQ=1,
故Q在以N为圆心,1为半径的半圆弧上,故L=π,故C选项正确;
对D:以D为原点建系如图,
则,设Q(m,n,0),m∈[0,],n∈[0,2],
所以,,,
设平面A1PQ的法向量为,
则,取,
所以C到平面A1PQ的距离为,
所以,
所以,
即或,
即或,
但当Q(m,n,0)满足时,直线在矩形ABCD外,
所以L2,故D选项正确.
故选:ACD.
三.填空题(共3小题)
12.(2025春 常州期中)已知向量的夹角为钝角,则实数t的取值范围为 (﹣∞,﹣4)∪(﹣4,5) .
【解答】解:因为向量的夹角为钝角,
则,解得t<5,
当共线时,由,即(﹣4,2,t)=λ(2,﹣1,2),解得t=﹣4,
所以当夹角为钝角时t∈(﹣∞,﹣4)∪(﹣4,5).
故答案为:(﹣∞,﹣4)∪(﹣4,5).
13.(2025春 淮安期中)《九章算术》是我国古代数学名著,它在几何学中的研究比西方早一千多年,书中将四个面均为直角三角形的四面体称为鳖臑.如图,四面体P﹣ABC为鳖臑,PA⊥平面ABC,AB⊥BC,且PA=AB=BC=1,则直线PB与平面PAC所成角的大小为 .
【解答】解:取AC的中点O,连接OB,OP,
因为AB⊥BC,且AB=BC=1,所以OB⊥AC,且OBAC,
因为PA⊥平面ABC,AC、OB 平面ABC,所以PA⊥AC,PA⊥OB,
又AC∩PA=A,AC、PA 平面PAC,所以OB⊥平面PAC,
所以∠OPB即为直线PB与平面PAC所成角,
在Rt△PAO中,PA=1,OA,所以OP,
所以tan∠OPB,
所以∠OPB,
即直线PB与平面PAC所成角的大小为.
故答案为:.
14.(2025春 邗江区校级期中)如图,在正方体ABCD﹣A1B1C1D1中,点P在线段B1C上运动,则下列结论正确的是 ①②④ .
①直线BD1⊥平面A1C1D
②三棱锥D﹣A1C1P的体积为定值
③异面直线AP与A1D所成角的取值范围是
④直线C1P与平面A1C1D所成角的正弦值的最大值为
【解答】解:对①,根据三垂线定理易知BD1⊥A1C1,BD1⊥A1D,从而可得BD1⊥平面A1C1D,∴①正确;
对②,易知B1C∥A1D,从而可得B1C∥平面A1C1D,
∴P到平面A1C1D距离为定值,又△A1C1D的面积也为定值,
∴三棱锥D﹣A1C1P的体积为定值,∴②正确;
对③,∵B1C∥A1D,
∴异面直线AP与A1D所成角即为相交直线AP与B1C所成角,
又易知△AB1C为等边三角形,
∴相交直线AP与B1C所成角的范围为[,],
即异面直线AP与A1D所成角的取值范围是[,],∴③错误;
对④,由①知BD1⊥平面A1C1D,
∴直线C1P与平面A1C1D所成角的正弦值为:
C1P与BD1所成角的余弦值,
如图将C1P对称平移至D1Q,
则C1P与BD1所成角的余弦值即为:
D1Q与BD1所成角的余弦值,其中Q为线段A1D上的动点,
又AB⊥平面ADD1A1,∴AB⊥D1Q,
∴当Q为A1D的中点时,D1Q与BD1所成角的余弦值最大,
最大值为,
∴直线C1P与平面A1C1D所成角的正弦值的最大值为,∴④正确.
故答案为:①②④.
四.解答题(共5小题)
15.(2025春 南京期中)如图,在三棱柱ABC﹣A1B1C1中,P是CC1的中点,△ABC、△C1BC均为边长为4的正三角形,且AC1=2,
(1)求证:平面ABC⊥平面CBB1C1;
(2)求直线A1B与平面ABP所成角的正弦值.
【解答】解:(1)证明:如图,取BC的中点O,连接AO,C1O,
因为△ABC、△C1BC均为边长为4的正三角形,
所以AO⊥CB,C1O⊥CB,A1O=C1O=2,△C1AO中,AO2,
所以AO⊥C1O,
又AO∩C1O=O,BC,C1O 平面CBB1C1,所以AO⊥平面CBB1C1,
又因为AO 平面ABC,
所以平面ABC⊥平面CBB1C1;
(2)以直线OA,OB,OC1所在直线分别为x,y,z轴建立如图所示的空间直角坐标系,
则A(2,0,0),B(0,2,0),C(0,﹣2,0),C1(0,0,2),B1(0,4,2),P(0,﹣1,),
由,得,,,,
设(x,y,z)是平面PAB的一个法向量,
则,
令,则,
设直线A1B与平面ABP所成角为θ,
则sinθ=|cos,|,
所以直线A1B与平面ABP所成角的正弦值为.
16.(2025春 兴化市校级月考)如图所示,在棱长为1的正方体ABCD﹣A1B1C1D1中,E为线段A1B1的中点,F为线段AB的中点.
(1)求点B到直线AC1的距离;
(2)求直线FC到平面AEC1的距离.
【解答】解:(1)以D1为坐标原点,分别以D1A1,D1C1,D1D所在直线为x,y,z轴建立空间直角坐标系,
则A(1,0,1),B(1,1,1),C(0,1,1),C1(0,1,0),E(1,,0),F(1,,1),
∴,,,,
,,
(1)取,,
,,则点B到直线AC1的距离为;
(2)∵,∴FC∥EC1,
而FC 平面AEC1,EC1 平面AEC1,∴FC∥平面AEC1,
则点F到平面AEC1的距离就是直线FC到平面AEC1的距离.
设平面AEC1的一个法向量为,
由,取y=2,得,
又,
∴直线FC到平面AEC1的距离为.
17.(2025 鼓楼区校级模拟)如图,在直四棱柱ABCD﹣A1B1C1D1中,AD=2,BC=CD,∠DCB=90°,∠DAB=45°,E,F分别为AD,AB的中点.
(1)求证:AD⊥BD;
(2)求证:平面BDC1∥平面EFD1;
(3)若CC1=2,P是线段D1F上的动点,求直线A1P与平面BDC1所成角的正弦值的最大值.
【解答】解:(1)证明:在直四棱柱ABCD﹣A1B1C1D1中,AD=2,BC=CD,
∠DCB=90°,∠DAB=45°,E,F分别为AD,AB的中点,
∵DC=BC,∠DCB=90°,
∴BD2,又AD=2,∴BD=AD=2,
又∠DAB=45°,∴∠ABD=45°,∴∠ADB=90°,∴AD⊥BD.
(2)证明:在直四棱柱ABCD﹣A1B1C1D1中,DD1⊥平面ABCD,
∵AD 平面ABCD,BD 平面ABCD,∴DD1⊥AD,DD1⊥BD,
∴DA,DB,DD1两两垂直,
以点D为坐标原点,以DA所在直线为x轴,DB所在直线为y轴,DD1所在直线为z轴,建立空间直角坐标系,如图,
设DD1=h(h>0),
则D(0,0,0),B(0,2,0),C1(﹣1,1,h),E(1,0,0),F(1,1,0),D1(0,0,h).
∴(0,2,0),(﹣1,1,h),(0,1,0),(﹣1,0,h),
设为平面BDC1的法向量,
则,令x1=h,得(h,0,1),
设平面EFD1的法向量,
则,取x=h,得(h,0,1),
∵∥,平面BDC1与平面EFD1不重合,
∴平面BDC1∥平面EFD1.
(3)CC1=2,P是线段D1F上的动点,
当CC1=2时,为平面BDC1的法向量,
D1(0,0,2),则(﹣1,﹣1,2),
设λ(﹣1,﹣1,2)=(﹣λ,﹣λ,2λ),(λ∈[0,1]),
∴P(1﹣λ,1﹣λ,2λ),∵A1(2,0,2),∴(﹣1﹣λ,1﹣λ,2λ﹣2),
设直线A1P与平面BDC1所成角为θ,
sinθ=|cos|
,
当且仅当时,等号成立,
∴若CC1=2,P是线段D1F上的动点,则直线A1P与平面BDC1所成角的正弦值的最大值为.
18.(2025春 盐城月考)如图,在四棱锥P﹣ABCD中,平面PAD⊥平面ABCD,E为AD的中点,PA⊥AD,BE∥CD,BE⊥AD,PA=AE=BE=2,CD=1.
(1)求A到平面PBC的距离;
(2)求直线PE与平面PBC所成角的正弦值;
(3)在线段PE上是否存在点M,使得DM∥平面PBC?若存在,求出点M的位置;若不存在,说明理由.
【解答】解:(1)因为平面PAD⊥平面ABCD,BE⊥AD,平面PAD∩平面ABCD=AD,
所以BE⊥平面PAD,
作Ez⊥AD,以E为原点,以,的方向分别为x轴,y轴的正方向,建立如图所示的空间直角坐标系E﹣xyz,
则点E(0,0,0),P(0,﹣2,2),A(0,﹣2,0),B(2,0,0),C(1,2,0),
D(0,2,0),
所以,,,
设平面PBC的法向量为,
则,所以,即,
取y=1,解得,
A到平面PBC的距离为;
(2)由(1)知,平面PBC的法向量为,
设直线PE与平面PBC所成角为θ,
则直线PE与平面PBC所成角的正弦值为:
,,
所以直线PE与平面PBC所成角的正弦值为;
(3)“线段PE上存在点M,使得DM∥平面PBC”等价于“”,
因为,
设,λ∈[0,1],
则M(0,2λ﹣2,2﹣2λ),.
由(2)知平面PBC的法向量为,
所以,
解得,
所以线段PE上存在点M,即PE中点,使得DM∥平面PBC.
19.(2025春 江苏校级期中)如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,且∠ABC=60°,PA⊥平面ABCD,PA=AB=2,点E,F为PC,PA的中点.
(1)求证:平面BDE⊥平面ABCD;
(2)二面角E﹣BD﹣F的大小;
(3)线段PC上是否存在点M,使得直线AM与平面BDF所成夹角为.若存在,求出M点的位置;若不存在,请说明理由.
【解答】解:(1)证明:连接AC与BD交于点O,连接EO,
∵底面ABCD为菱形,∴点O为AC的中点,
∵点E为PC的中点∴EO∥PA,
又∵PA⊥平面ABCD,∴EO⊥平面ABCD,
又∵EO 平面BDE,
∴平面BDE⊥平面ABCD.
(2)∵EO⊥平面ABCD,且底面ABCD为菱形,∴OB,OC,OE两两垂直.
以O为原点,以向量方向为x,y,z轴正方向建立如图所示空间直角坐标系,
∵底面ABCD为菱形,且∠ABC=60°,则△ABC为等边三角形,
PA=AB=2,∴,
∵O,E分别为AC,PC的中点,∴,
则,
则,
设平面BFD的一个法向量为,
则,有,
令y=1,则,
∵底面ABCD为菱形,∴OC⊥BD,
∵平面BDE⊥平面ABCD,且平面BDE∩平面ABCD=BD,OC 平面ABCD,
∴OC⊥平面BDE,
∴为平面BDE的一个法向量,
设二面角E﹣BD﹣F大小为θ,
则.
∴二面角E﹣BD﹣F的大小为;
(3)不存在,理由如下:
∵点M在线段PC上,设,
由P(0,﹣1,2),C(0,1,0),A(0,﹣1,0)可得,
则,则M(0,2λ﹣1,2﹣2λ),则,
由题意,若直线AM与平面BDF所成夹角为,
则,
整理得2λ2﹣2λ﹣1=0,解出.
又∵0≤λ≤1,∴不符合题意,故线段PC上不存在这样的点M.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
