【江苏省各地区真题汇编】立体几何初步考前专题特训-2025年高考数学(含解析)
文档属性
| 名称 | 【江苏省各地区真题汇编】立体几何初步考前专题特训-2025年高考数学(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-26 21:25:55 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【江苏省各地区真题汇编】立体几何初步考前专题特训-2025年高考数学
一.选择题(共8小题)
1.(2025 南通校级模拟)若圆柱的侧面的展开图的周长为4,则该圆柱体积最大为( )
A. B. C. D.
2.(2025 武进区校级一模)已知长方体ABCD﹣A1B1C1D1,E是棱C1D1的中点,平面AB1E将长方体分割成两部分,则体积较大部分与体积较小部分的体积之比为( )
A. B.2 C. D.
3.(2023秋 海门区校级月考)如图,圆锥的轴截面SAB是正三角形,O为底面圆的圆心,D为SO的中点,点C在底面圆的圆周上,且△ABC是等腰直角三角形,则直线CD与AS所成角的余弦值为( )
A. B. C. D.
4.(2025春 润州区校级期中)下列叙述中,正确的是( )
A.因为P∈α,Q∈α,所以PQ∈α
B.因为P∈α,Q∈β,所以α∩β=PQ
C.因为AB α,C∈AB,D∈AB,所以CD∈α
D.因为AB α,AB β,所以α∩β=AB
5.(2024春 锡山区校级期末)若底面半径为r,母线长为l的圆锥的表面积与直径为l的球的表面积相等,则( )
A. B. C. D.
6.(2025 姜堰区模拟)在三棱锥S﹣ABC中,底面△ABC为斜边的等腰直角三角形,顶点S在底面ABC上的射影为AC的中点.若SA=2,E为线段AB上的一个动点,则SE+CE的最小值为( )
A. B. C. D.
7.(2025春 淮安期中)在直三棱柱ABC﹣A1B1C1中,AB⊥AC,AB=AC=1,,则异面直线AC1与BC所成角的余弦值为( )
A. B. C. D.
8.(2025 江苏校级模拟)如图是一个棱长为2的正方体被过棱A1B1、A1D1的中点M、N,顶点A和过点N顶点D、C1的两个截面截去两个角后所得的几何体,则该几何体的体积为( )
A.5 B.6 C.7 D.8
二.多选题(共3小题)
(多选)9.(2025 江苏校级模拟)如图,圆锥的底面直径AB=2,母线VA=3,点C是母线VB的中点.以下结论正确的是( )
A.沿圆锥的侧面从点A到达点C的最短距离为
B.圆锥的外接球表面积为
C.过点C作平行于母线VA的平面,截圆锥所得抛物线的焦准距为3
D.过点V作动直线l,满足与母线VA成角,直线l形成的图形被圆锥底面所在平面截得的图形为椭圆
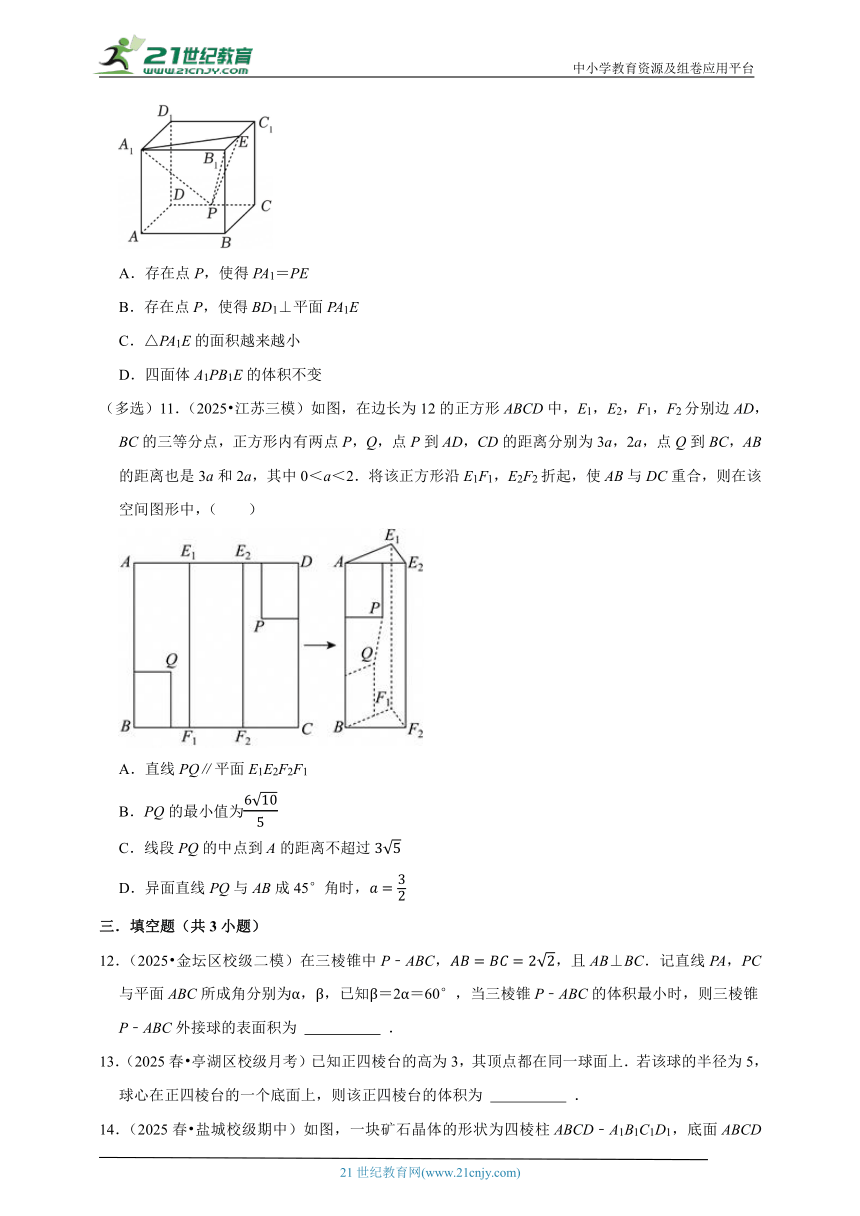
(多选)10.(2024秋 鼓楼区校级期末)如图,在正方体ABCD﹣A1B1C1D1中,E为棱B1C1的中点,动点P沿着棱DC从点D向点C移动,对于下列四个结论,正确的是( )
A.存在点P,使得PA1=PE
B.存在点P,使得BD1⊥平面PA1E
C.△PA1E的面积越来越小
D.四面体A1PB1E的体积不变
(多选)11.(2025 江苏三模)如图,在边长为12的正方形ABCD中,E1,E2,F1,F2分别边AD,BC的三等分点,正方形内有两点P,Q,点P到AD,CD的距离分别为3a,2a,点Q到BC,AB的距离也是3a和2a,其中0<a<2.将该正方形沿E1F1,E2F2折起,使AB与DC重合,则在该空间图形中,( )
A.直线PQ∥平面E1E2F2F1
B.PQ的最小值为
C.线段PQ的中点到A的距离不超过
D.异面直线PQ与AB成45°角时,
三.填空题(共3小题)
12.(2025 金坛区校级二模)在三棱锥中P﹣ABC,,且AB⊥BC.记直线PA,PC与平面ABC所成角分别为α,β,已知β=2α=60°,当三棱锥P﹣ABC的体积最小时,则三棱锥P﹣ABC外接球的表面积为 .
13.(2025春 亭湖区校级月考)已知正四棱台的高为3,其顶点都在同一球面上.若该球的半径为5,球心在正四棱台的一个底面上,则该正四棱台的体积为 .
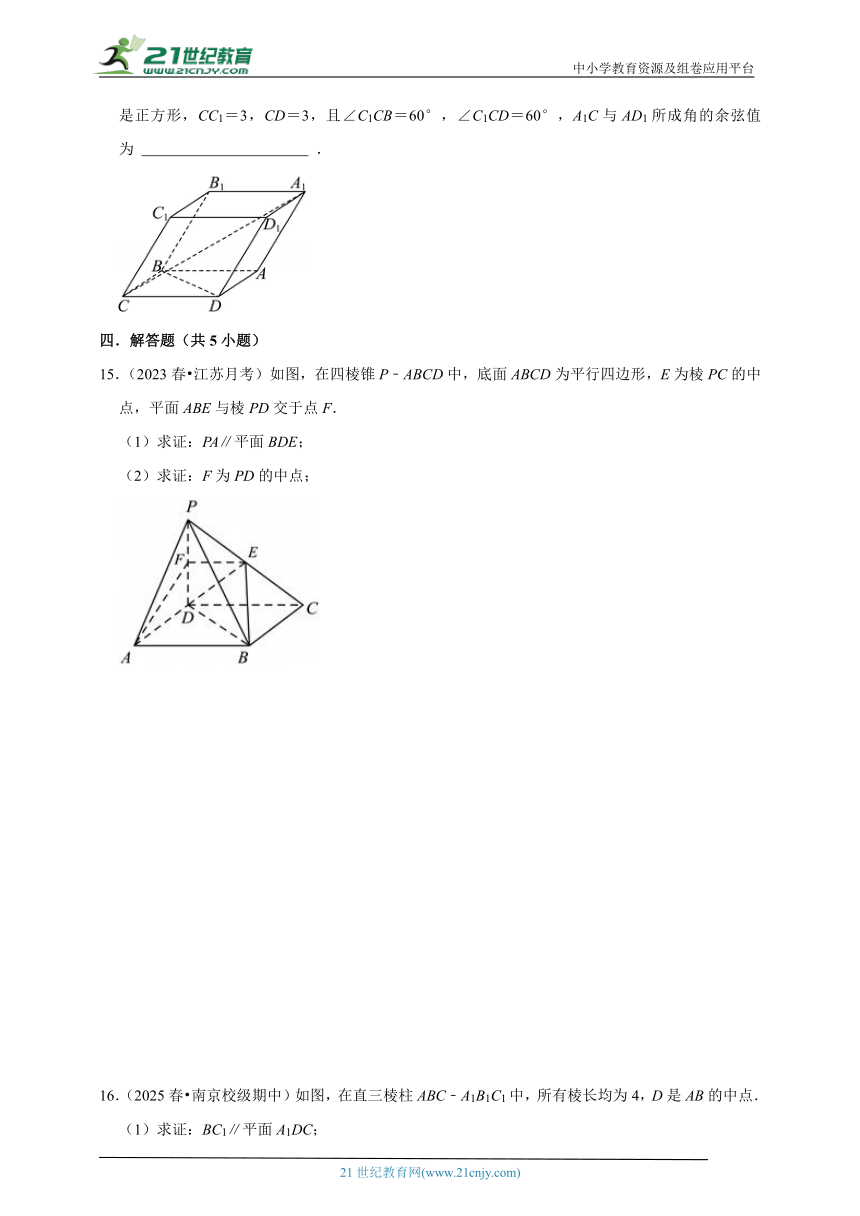
14.(2025春 盐城校级期中)如图,一块矿石晶体的形状为四棱柱ABCD﹣A1B1C1D1,底面ABCD是正方形,CC1=3,CD=3,且∠C1CB=60°,∠C1CD=60°,A1C与AD1所成角的余弦值为 .
四.解答题(共5小题)
15.(2023春 江苏月考)如图,在四棱锥P﹣ABCD中,底面ABCD为平行四边形,E为棱PC的中点,平面ABE与棱PD交于点F.
(1)求证:PA∥平面BDE;
(2)求证:F为PD的中点;
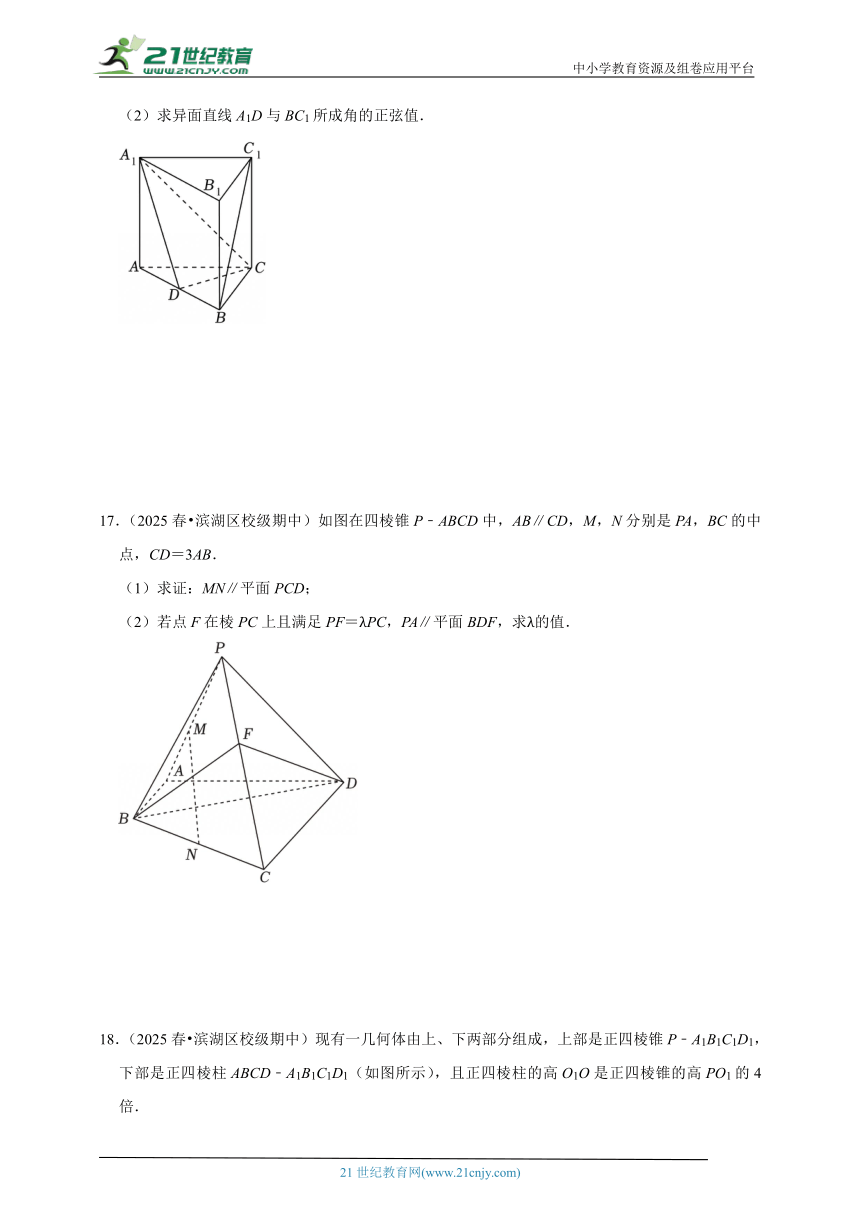
16.(2025春 南京校级期中)如图,在直三棱柱ABC﹣A1B1C1中,所有棱长均为4,D是AB的中点.
(1)求证:BC1∥平面A1DC;
(2)求异面直线A1D与BC1所成角的正弦值.
17.(2025春 滨湖区校级期中)如图在四棱锥P﹣ABCD中,AB∥CD,M,N分别是PA,BC的中点,CD=3AB.
(1)求证:MN∥平面PCD;
(2)若点F在棱PC上且满足PF=λPC,PA∥平面BDF,求λ的值.
18.(2025春 滨湖区校级期中)现有一几何体由上、下两部分组成,上部是正四棱锥P﹣A1B1C1D1,下部是正四棱柱ABCD﹣A1B1C1D1(如图所示),且正四棱柱的高O1O是正四棱锥的高PO1的4倍.
(1)若AB=6,PO1=2,求该几何体的体积.
(2)若正四棱锥的侧棱长为6,PO1=2.
(i)求正四棱锥P﹣A1B1C1D1的侧面积.
(i)若Q,N分别是线段A1B1,PB1上的动点,求AQ+QN+NC1的最小值.
19.(2025春 鼓楼区校级月考)在多面体ABCDPE中(如图),底面ABCD为梯形,AB⊥AD,AB∥CD,F为PA的中点,,,四边形PDCE为矩形,平面PDCE⊥平面ABCD.
(1)求证:平面PBD⊥平面ABCD;
(2)求三棱锥P﹣ABD外接球的体积;
(3)在线段EF上是否存在一点Q,使得BQ与平面PBC所成角的大小为若存在,求出FQ的长;若不存在,请说明理由.
【江苏省各地区真题汇编】立体几何初步考前专题特训-2025年高考数学
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 A C C D B A C C
二.多选题(共3小题)
题号 9 10 11
答案 ABD ACD ABD
一.选择题(共8小题)
1.(2025 南通校级模拟)若圆柱的侧面的展开图的周长为4,则该圆柱体积最大为( )
A. B. C. D.
【解答】解:设圆柱母线长为l,底面半径为r,则,
而圆柱体积V=πr2l=πr2(2﹣2πr),其中.
则V′=4πr﹣6π2r2,
当r∈(0,)时,V′>0,V=πr2(2﹣2πr)为增函数,
当r∈()时,V′<0,V=πr2(2﹣2πr)为减函数,
故.
故选:A.
2.(2025 武进区校级一模)已知长方体ABCD﹣A1B1C1D1,E是棱C1D1的中点,平面AB1E将长方体分割成两部分,则体积较大部分与体积较小部分的体积之比为( )
A. B.2 C. D.
【解答】解:因为长方体ABCD﹣A1B1C1D1,E是棱C1D1的中点,平面AB1E将长方体分割成两部分,
所以作出示意图如下:
取DD1的中点为F,又E是棱C1D1的中点,
所以可知EF∥C1D∥AB1,
所以E,F,A,B1四点共面,
根据长方体性质,△D1EF与△A1B1A相似,相似比为,且平面D1EF∥平面A1B1A,
所以AF,A1D1,B1E交于同一点,
所以长方体被平面AB1EF割成的体积较小部分为三棱台D1EF﹣A1B1A,
设长方体的各棱长为AB=a,AD=b,AA1=c,则长方体的体积为V=abc,
再由棱台体积公式可得
,
较大部分的体积为;
所以体积较大部分与体积较小部分的体积之比为.
故选:C.
3.(2023秋 海门区校级月考)如图,圆锥的轴截面SAB是正三角形,O为底面圆的圆心,D为SO的中点,点C在底面圆的圆周上,且△ABC是等腰直角三角形,则直线CD与AS所成角的余弦值为( )
A. B. C. D.
【解答】解:取OA的中点E,
由D为SO的中点,
则DE∥SA,
则直线CD与AS所成的角为∠CDE(或其补角),
不妨设|AB|=2,
又圆锥的轴截面SAB是正三角形,O为底面圆的圆心,D为SO的中点,点C在底面圆的圆周上,且△ABC是等腰直角三角形,
则|DE|,,,
在△CDE中,由余弦定理可得cos∠CDE,
即直线CD与AS所成角的余弦值为,
故选:C.
4.(2025春 润州区校级期中)下列叙述中,正确的是( )
A.因为P∈α,Q∈α,所以PQ∈α
B.因为P∈α,Q∈β,所以α∩β=PQ
C.因为AB α,C∈AB,D∈AB,所以CD∈α
D.因为AB α,AB β,所以α∩β=AB
【解答】解:因为P∈α,Q∈α,所以PQ α,故A错误;
由P∈α,Q∈β,推不出α∩β=PQ,故B错误;
因为AB α,C∈AB,D∈AB,所以CD α,故C错误;
因为AB α,AB β,所以A∈(α∩β)且B∈(α∩β),故D正确.
故选:D.
5.(2024春 锡山区校级期末)若底面半径为r,母线长为l的圆锥的表面积与直径为l的球的表面积相等,则( )
A. B. C. D.
【解答】解:因为底面半径为r,母线长为l的圆锥的表面积与直径为l的球的表面积相等,
又圆锥的表面积为πrl+πr2,球的表面积为,
所以πrl+πr2=πl2,即,
解得.
故选:B.
6.(2025 姜堰区模拟)在三棱锥S﹣ABC中,底面△ABC为斜边的等腰直角三角形,顶点S在底面ABC上的射影为AC的中点.若SA=2,E为线段AB上的一个动点,则SE+CE的最小值为( )
A. B. C. D.
【解答】解:如图,在三棱锥S﹣ABC中,设点O为线段AC的中点,连接BO,SO,
由题易知:平面ABC,
在Rt△ABC中,,故,
所以△SAB是边长为2的等边三角形,
将△SAB展开到与△ABC共面,如图所示,
则SE+CE≥SC,当且仅当S,E,C三点共线时等号成立,即SE+CE取得最小值,
在△SBC中,,
由余弦定理可得:,
所以,
即SE+CE的最小值为.
故选:A.
7.(2025春 淮安期中)在直三棱柱ABC﹣A1B1C1中,AB⊥AC,AB=AC=1,,则异面直线AC1与BC所成角的余弦值为( )
A. B. C. D.
【解答】解:连接AB1,因为BC∥B1C1,
所以∠B1C1A等于异面直线AC1与BC所成的角,
因为AB⊥AC,AB=AC=1,,所以BC=B1C1,
AC1=AB1,
在△AB1C1中,由余弦定理可得cos∠B1C1A
.
所以异面直线AC1与BC所成角的余弦值为.
故选:C.
8.(2025 江苏校级模拟)如图是一个棱长为2的正方体被过棱A1B1、A1D1的中点M、N,顶点A和过点N顶点D、C1的两个截面截去两个角后所得的几何体,则该几何体的体积为( )
A.5 B.6 C.7 D.8
【解答】解:如图将正方体还原可得如下图形:
则,,
所以该几何体的体积 .
故选:C.
二.多选题(共3小题)
(多选)9.(2025 江苏校级模拟)如图,圆锥的底面直径AB=2,母线VA=3,点C是母线VB的中点.以下结论正确的是( )
A.沿圆锥的侧面从点A到达点C的最短距离为
B.圆锥的外接球表面积为
C.过点C作平行于母线VA的平面,截圆锥所得抛物线的焦准距为3
D.过点V作动直线l,满足与母线VA成角,直线l形成的图形被圆锥底面所在平面截得的图形为椭圆
【解答】解:对于A,沿母线VA展开圆锥侧面如图所示,
因为底面直径AB=2,所以底面圆周长为2π,即展开后扇形弧长为2π,
因为母线VA=3,所以展开后扇形半径为3,则扇形圆心角∠AVA',
所以∠AVB,点A到VB的距离为3sin,
即沿圆锥的侧面从点A到达点C的最短距离为,故A正确;
对于B,由对称性知外接球球心O在圆锥的高上,
设O到底面的距离为d,外接球半径为R,
因为母线长为3,底面半径为1,所以圆锥的高为2,
则R2=12+d2,解得d,R,
则圆锥的外接球表面积等于4πR2,故B正确;
对于C,点C为母线VB中点,过点C与母线VA的平面必过底面圆圆心,交底面圆与E、F,如图,
EF=2,设底面圆圆心为M,则MCVA,
以C为坐标原点,CM所在直线为x轴,在截面内建立平面直角坐标系,
如图,
设抛物线方程为y2=2px,将点E(,1)代入,得p,故焦准距为,C错误;
对于D,由已知圆锥底面与直线VA所成角α满足cosα,动直线l与VA夹角β为,
其形成轨迹为一个圆锥面,VA为该圆锥的轴,l为母线,
因为cosβ,所以α>β,所以直线l形成的图形被圆锥底面所在平面截得的图形为椭圆,D正确.
故选ABD.
(多选)10.(2024秋 鼓楼区校级期末)如图,在正方体ABCD﹣A1B1C1D1中,E为棱B1C1的中点,动点P沿着棱DC从点D向点C移动,对于下列四个结论,正确的是( )
A.存在点P,使得PA1=PE
B.存在点P,使得BD1⊥平面PA1E
C.△PA1E的面积越来越小
D.四面体A1PB1E的体积不变
【解答】解:对于A,设正方体棱长为2,DP=m(0≤m≤2),由AA1⊥平面ABCD,AP 平面ABCD,得AA1⊥AP,
同理PC⊥EC,所以AD2+DP2=8+m2,
PE2=PC2+CE2=(2﹣m)2+5,由8+m2=(2﹣m)2+5,解得,
所以存在P使得PA1=PE,故A正确;
对于B,以D为坐标原点,DA、DC、DD1所在直线分别为x、y、z轴建立空间直角坐标系,如下图,
设正方体棱长为2,则A1(2,0,2),E(1,2,2),B(2,2,0),D1(0,0,2),
所以(﹣1,2,0),,
,所以BD1不可能与A1E垂直,故BD1⊥平面PA1E也不可能成立,故B错误;
对于C,在B中所建空间直角坐标系中,设P(0,m,0)(0≤m≤2),则(1,2﹣m,2),
,,
所以,
设P到直线A1E的距离为d,则d
,
由二次函数性质知0≤m≤2时,y=(m﹣4)2+20递减,所以d递减,
又不变,ΔA1PE的面积为 d,所以ΔA1PE的面积递减,故C正确;
对于D,正方体中,CD∥平面A1B1C1D1,P∈CD,所以P到平面A1B1C1D1的距离不变,
即P到平面A1B1E的距离不变,而ΔA1B1E面积不变,因此三棱锥P=A1B1E即四面体A1PB1E的体积不变,故D正确.
综上,ACD正确.
故选:ACD.
(多选)11.(2025 江苏三模)如图,在边长为12的正方形ABCD中,E1,E2,F1,F2分别边AD,BC的三等分点,正方形内有两点P,Q,点P到AD,CD的距离分别为3a,2a,点Q到BC,AB的距离也是3a和2a,其中0<a<2.将该正方形沿E1F1,E2F2折起,使AB与DC重合,则在该空间图形中,( )
A.直线PQ∥平面E1E2F2F1
B.PQ的最小值为
C.线段PQ的中点到A的距离不超过
D.异面直线PQ与AB成45°角时,
【解答】解:如图,
取E1E2中点O1,F1F2的中点O,连接OB,OO1,
因为BF2=F2F1=F1B=4,所以BO⊥F1F2,
因为E1F1⊥F1B,E1F1⊥F1F2,又F1B∩F1F2,F1B,F1F2 面BF1F2,
所以E1F1⊥面BF1F2,又OO1∥E1F1,所以OO1⊥面BF1F2,
故OB,OF2,OO1两两垂直,建立如图所示的空间直角坐标系,
设QH⊥BF1于H,PM⊥BF2于M,过H作HK⊥OB于K,
易知,BH=2a,又,
所以,
又QH=3a,
所以,同理可知,
所以,
对于选项A,易知平面E1E2F2F1的一个法向量为,
因为,
显然QP 平面E1E2F2F1,所以PQ∥平面E1E2F2F1,故选项A正确;
对于选项B,因为,
令y=40a2﹣144a+144,其中0<a<2,
对称轴,所以,
所以,故选项B正确;
对于选项C,因为PQ的中点,,
所以|AS|3,故选项C错误;
对于选项D,因为,所以,
所以,整理得到2a2﹣9a+9=0,
解得或a=3(舍),故选项D正确.
故选:ABD.
三.填空题(共3小题)
12.(2025 金坛区校级二模)在三棱锥中P﹣ABC,,且AB⊥BC.记直线PA,PC与平面ABC所成角分别为α,β,已知β=2α=60°,当三棱锥P﹣ABC的体积最小时,则三棱锥P﹣ABC外接球的表面积为 16π .
【解答】解:设点P在平面ABC内的投影为P',因为直线PA,PC与平面ABC所成角分别为α,β,且β=2α=60°,则α=30°,
根据线面夹角关系可知,,
所以3|P'C|=|P'A|,
由阿波罗尼斯圆可知,投影P'在圆上运动,以AC所在直线为x轴,过AC的中点O作垂线,建立如图所示直角坐标系,
因为,AB=BC,且AB⊥BC,所以AC,OB=OA=2,
令P'(x,y),由题可知A(﹣2,0),B(0,2),C(2,0),
则,
化简得,
可知P'在以为圆心,半径为的圆上,
当|P'C|最小时,|P'P|最小,即三棱锥P﹣ABC的体积最小,
此时P'(1,0),,,,
∴P点在底面ABC上的射影P'在AC上,且∠APC=90°,又∠ABC=90°,
∴此时三棱锥P﹣ABC的外接球的球心为AC的中点,
外接球的半径,.
故答案为:16π.
13.(2025春 亭湖区校级月考)已知正四棱台的高为3,其顶点都在同一球面上.若该球的半径为5,球心在正四棱台的一个底面上,则该正四棱台的体积为 122 .
【解答】解:因为正四棱台的高为3,其顶点都在同一球面上,
且该球的半径为5,球心在正四棱台的一个底面上,
设球心所在底面为下底面,正四棱台的高为3,球半径为5,
设上底面边长为a,则上底面中心到顶点距离为,
根据勾股定理,即,解得,
因为球心在下底面,下底面中心到顶点距离就是球半径5,
设下底面边长为b,则,解得,
根据正四棱台体积公式(其中h是高,S是下底面积,S′是上底面积),
下底面积,上底面积S′=a2=32,
已知高h=3,则体积.
故答案为:122.
14.(2025春 盐城校级期中)如图,一块矿石晶体的形状为四棱柱ABCD﹣A1B1C1D1,底面ABCD是正方形,CC1=3,CD=3,且∠C1CB=60°,∠C1CD=60°,A1C与AD1所成角的余弦值为 .
【解答】解:分别取,则,
且,
而,
由,
,
,
设A1C与AD1的所成角为θ,
则cosθ=|cos,|.
故答案为:.
四.解答题(共5小题)
15.(2023春 江苏月考)如图,在四棱锥P﹣ABCD中,底面ABCD为平行四边形,E为棱PC的中点,平面ABE与棱PD交于点F.
(1)求证:PA∥平面BDE;
(2)求证:F为PD的中点;
【解答】证明:(1)如图所示:
连接AC交BD于点G,连接GE,
因为ABCD为平行四边形,
所以G为AC的中点,
又E为PC的中点,
所以GE∥PA,
又PA 平面BDE,GE 平面BDE,
所以PA∥平面BDE;
(2)因为底面ABCD为平行四边形,
所以AB∥CD,
又AB 平面ABCD,CD 平面ABCD,
所以CD∥平面ABEF,
又平面ABEF∩平面PDC=EF,
所以CD∥EF,
又因为E为PC的中点,
所以F为PD的中点.
16.(2025春 南京校级期中)如图,在直三棱柱ABC﹣A1B1C1中,所有棱长均为4,D是AB的中点.
(1)求证:BC1∥平面A1DC;
(2)求异面直线A1D与BC1所成角的正弦值.
【解答】(1)证明:连接AC1交A1C于O,
在直三棱柱ABC﹣A1B1C1中,所有棱长均为4,
因此四边形AA1C1C是正方形,所以O是AC1的中点,而D是AB的中点,
因此有OD∥BC1,而OD 平面A1DC,BC1 平面A1DC,
所以BC1∥平面A1DC;
(2)解:由(1)可知:OD∥BC1,
因此异面直线A1D与BC1所成角为∠A1DO(或其补角),
因为AA1C1C是正方形,所以,
在直三棱柱ABC﹣A1B1C1中,所有棱长均为4,
因此四边形BB1C1C是正方形,因此有,
在直三棱柱ABC﹣A1B1C1中,侧棱垂直于底面,因此也就垂直底面中任何直线,
因此有,
由余弦定理可知:,
因此.
17.(2025春 滨湖区校级期中)如图在四棱锥P﹣ABCD中,AB∥CD,M,N分别是PA,BC的中点,CD=3AB.
(1)求证:MN∥平面PCD;
(2)若点F在棱PC上且满足PF=λPC,PA∥平面BDF,求λ的值.
【解答】(1)证明:取PB的中点E,连接ME,EN,
因为AB∥CD,M,N分别是PA,BC的中点,
所以EM∥AB,EN∥PC,
所以ME∥CD,
ME 平面PCD,EN 平面PCD,CD 平面PCD,PC 平面PCD,
所以ME∥平面PCD,EN∥平面PCD,
且ME∩EN=E,
所以平面MEN∥平面PCD,
又因为MN 平面MEN,
所以MN∥平面PCD;
(2)解:连接AC,交BD于O,连接OF,又因为DC=3AB,AB∥CD,
所以AOOC,
因为PA∥平面BDF,PA 平面PAC,
平面PAC∩平面BDF=OF,
所以PA∥OF,
所以,
所以PFFC,可得PFPC,
又因为PF=λPC,
可得λ.
18.(2025春 滨湖区校级期中)现有一几何体由上、下两部分组成,上部是正四棱锥P﹣A1B1C1D1,下部是正四棱柱ABCD﹣A1B1C1D1(如图所示),且正四棱柱的高O1O是正四棱锥的高PO1的4倍.
(1)若AB=6,PO1=2,求该几何体的体积.
(2)若正四棱锥的侧棱长为6,PO1=2.
(i)求正四棱锥P﹣A1B1C1D1的侧面积.
(i)若Q,N分别是线段A1B1,PB1上的动点,求AQ+QN+NC1的最小值.
【解答】解:(1)由条件可知,正四棱柱的高O1O=8,
所以正四棱柱的体积为6×6×8=288,
三棱锥P﹣A1B1C1D1的体积为,
所以该几何体的体积为288+24=312;
(2)(i),
所以,
正四棱锥P﹣A1B1C1D1侧面的高为,
所以正四棱锥的侧面积为;
(ii)如图,将长方形ABB1A1,△PA1B1和△PB1C1展开在一个平面,
PA1=PB1=PC1=6,A1B1=B1C1=8,
设∠A1B1P=α,,A1B1=AA1=8,,
,所以,
所以,
,
,
当A,Q,N,C1四点共线时,AQ+QN+NC1最短,
所以,
所以AQ+QN+NC1的最小值为.
19.(2025春 鼓楼区校级月考)在多面体ABCDPE中(如图),底面ABCD为梯形,AB⊥AD,AB∥CD,F为PA的中点,,,四边形PDCE为矩形,平面PDCE⊥平面ABCD.
(1)求证:平面PBD⊥平面ABCD;
(2)求三棱锥P﹣ABD外接球的体积;
(3)在线段EF上是否存在一点Q,使得BQ与平面PBC所成角的大小为若存在,求出FQ的长;若不存在,请说明理由.
【解答】解:(1)证明:因为四边形PDCE为矩形,
所以PD⊥CD,
因为平面PDCE⊥平面ABCD,
平面PDCE∩平面ABCD=CD,PD 平面PDCE,
所以PD⊥平面ABCD,
又因为PD 平面PBD,
所以平面PBD⊥平面ABCD;
(2)由(1)知PD⊥平面ABCD,
BD 平面ABCD,
所以PD⊥BD,
所以Rt△PBD的外心O在BD的中点,
所以OG∥PD,所以OG⊥平面ABCD,
AB⊥AD,所以Rt△ABD的外心G在BD的中点,
所以点O为三棱锥P﹣ABD外接球的球心,
,,
所以外接球的半径,
则三棱锥P﹣ABD外接球的体积为;
(3)因为AD⊥DC,PD⊥平面ABCD,
所以以D为原点,以DA,DC,DP所在直线为x轴,y轴,z轴建立空间直角坐标系,
则A(1,0,0),,,B(1,1,0),C(0,2,0),,
设线段EF上存在一点Q,使得BQ与平面PBC所成角的大小为,
设Q(x1,y1,z1),,λ∈[0,1],
则.
所以,,,
设平面PBC的法向量为,
则,
取x=1,则y=1,,
则,
因为,
又BQ与平面PBC所成角的大小为,
所以,
即,
整理得λ2=1,所以λ=1,
此时点Q与点E重合,
所以,
则.
综上:在线段EF上存在一点Q,使得BQ与平面PBC所成角的大小为,此时FQ的长度为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【江苏省各地区真题汇编】立体几何初步考前专题特训-2025年高考数学
一.选择题(共8小题)
1.(2025 南通校级模拟)若圆柱的侧面的展开图的周长为4,则该圆柱体积最大为( )
A. B. C. D.
2.(2025 武进区校级一模)已知长方体ABCD﹣A1B1C1D1,E是棱C1D1的中点,平面AB1E将长方体分割成两部分,则体积较大部分与体积较小部分的体积之比为( )
A. B.2 C. D.
3.(2023秋 海门区校级月考)如图,圆锥的轴截面SAB是正三角形,O为底面圆的圆心,D为SO的中点,点C在底面圆的圆周上,且△ABC是等腰直角三角形,则直线CD与AS所成角的余弦值为( )
A. B. C. D.
4.(2025春 润州区校级期中)下列叙述中,正确的是( )
A.因为P∈α,Q∈α,所以PQ∈α
B.因为P∈α,Q∈β,所以α∩β=PQ
C.因为AB α,C∈AB,D∈AB,所以CD∈α
D.因为AB α,AB β,所以α∩β=AB
5.(2024春 锡山区校级期末)若底面半径为r,母线长为l的圆锥的表面积与直径为l的球的表面积相等,则( )
A. B. C. D.
6.(2025 姜堰区模拟)在三棱锥S﹣ABC中,底面△ABC为斜边的等腰直角三角形,顶点S在底面ABC上的射影为AC的中点.若SA=2,E为线段AB上的一个动点,则SE+CE的最小值为( )
A. B. C. D.
7.(2025春 淮安期中)在直三棱柱ABC﹣A1B1C1中,AB⊥AC,AB=AC=1,,则异面直线AC1与BC所成角的余弦值为( )
A. B. C. D.
8.(2025 江苏校级模拟)如图是一个棱长为2的正方体被过棱A1B1、A1D1的中点M、N,顶点A和过点N顶点D、C1的两个截面截去两个角后所得的几何体,则该几何体的体积为( )
A.5 B.6 C.7 D.8
二.多选题(共3小题)
(多选)9.(2025 江苏校级模拟)如图,圆锥的底面直径AB=2,母线VA=3,点C是母线VB的中点.以下结论正确的是( )
A.沿圆锥的侧面从点A到达点C的最短距离为
B.圆锥的外接球表面积为
C.过点C作平行于母线VA的平面,截圆锥所得抛物线的焦准距为3
D.过点V作动直线l,满足与母线VA成角,直线l形成的图形被圆锥底面所在平面截得的图形为椭圆
(多选)10.(2024秋 鼓楼区校级期末)如图,在正方体ABCD﹣A1B1C1D1中,E为棱B1C1的中点,动点P沿着棱DC从点D向点C移动,对于下列四个结论,正确的是( )
A.存在点P,使得PA1=PE
B.存在点P,使得BD1⊥平面PA1E
C.△PA1E的面积越来越小
D.四面体A1PB1E的体积不变
(多选)11.(2025 江苏三模)如图,在边长为12的正方形ABCD中,E1,E2,F1,F2分别边AD,BC的三等分点,正方形内有两点P,Q,点P到AD,CD的距离分别为3a,2a,点Q到BC,AB的距离也是3a和2a,其中0<a<2.将该正方形沿E1F1,E2F2折起,使AB与DC重合,则在该空间图形中,( )
A.直线PQ∥平面E1E2F2F1
B.PQ的最小值为
C.线段PQ的中点到A的距离不超过
D.异面直线PQ与AB成45°角时,
三.填空题(共3小题)
12.(2025 金坛区校级二模)在三棱锥中P﹣ABC,,且AB⊥BC.记直线PA,PC与平面ABC所成角分别为α,β,已知β=2α=60°,当三棱锥P﹣ABC的体积最小时,则三棱锥P﹣ABC外接球的表面积为 .
13.(2025春 亭湖区校级月考)已知正四棱台的高为3,其顶点都在同一球面上.若该球的半径为5,球心在正四棱台的一个底面上,则该正四棱台的体积为 .
14.(2025春 盐城校级期中)如图,一块矿石晶体的形状为四棱柱ABCD﹣A1B1C1D1,底面ABCD是正方形,CC1=3,CD=3,且∠C1CB=60°,∠C1CD=60°,A1C与AD1所成角的余弦值为 .
四.解答题(共5小题)
15.(2023春 江苏月考)如图,在四棱锥P﹣ABCD中,底面ABCD为平行四边形,E为棱PC的中点,平面ABE与棱PD交于点F.
(1)求证:PA∥平面BDE;
(2)求证:F为PD的中点;
16.(2025春 南京校级期中)如图,在直三棱柱ABC﹣A1B1C1中,所有棱长均为4,D是AB的中点.
(1)求证:BC1∥平面A1DC;
(2)求异面直线A1D与BC1所成角的正弦值.
17.(2025春 滨湖区校级期中)如图在四棱锥P﹣ABCD中,AB∥CD,M,N分别是PA,BC的中点,CD=3AB.
(1)求证:MN∥平面PCD;
(2)若点F在棱PC上且满足PF=λPC,PA∥平面BDF,求λ的值.
18.(2025春 滨湖区校级期中)现有一几何体由上、下两部分组成,上部是正四棱锥P﹣A1B1C1D1,下部是正四棱柱ABCD﹣A1B1C1D1(如图所示),且正四棱柱的高O1O是正四棱锥的高PO1的4倍.
(1)若AB=6,PO1=2,求该几何体的体积.
(2)若正四棱锥的侧棱长为6,PO1=2.
(i)求正四棱锥P﹣A1B1C1D1的侧面积.
(i)若Q,N分别是线段A1B1,PB1上的动点,求AQ+QN+NC1的最小值.
19.(2025春 鼓楼区校级月考)在多面体ABCDPE中(如图),底面ABCD为梯形,AB⊥AD,AB∥CD,F为PA的中点,,,四边形PDCE为矩形,平面PDCE⊥平面ABCD.
(1)求证:平面PBD⊥平面ABCD;
(2)求三棱锥P﹣ABD外接球的体积;
(3)在线段EF上是否存在一点Q,使得BQ与平面PBC所成角的大小为若存在,求出FQ的长;若不存在,请说明理由.
【江苏省各地区真题汇编】立体几何初步考前专题特训-2025年高考数学
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 A C C D B A C C
二.多选题(共3小题)
题号 9 10 11
答案 ABD ACD ABD
一.选择题(共8小题)
1.(2025 南通校级模拟)若圆柱的侧面的展开图的周长为4,则该圆柱体积最大为( )
A. B. C. D.
【解答】解:设圆柱母线长为l,底面半径为r,则,
而圆柱体积V=πr2l=πr2(2﹣2πr),其中.
则V′=4πr﹣6π2r2,
当r∈(0,)时,V′>0,V=πr2(2﹣2πr)为增函数,
当r∈()时,V′<0,V=πr2(2﹣2πr)为减函数,
故.
故选:A.
2.(2025 武进区校级一模)已知长方体ABCD﹣A1B1C1D1,E是棱C1D1的中点,平面AB1E将长方体分割成两部分,则体积较大部分与体积较小部分的体积之比为( )
A. B.2 C. D.
【解答】解:因为长方体ABCD﹣A1B1C1D1,E是棱C1D1的中点,平面AB1E将长方体分割成两部分,
所以作出示意图如下:
取DD1的中点为F,又E是棱C1D1的中点,
所以可知EF∥C1D∥AB1,
所以E,F,A,B1四点共面,
根据长方体性质,△D1EF与△A1B1A相似,相似比为,且平面D1EF∥平面A1B1A,
所以AF,A1D1,B1E交于同一点,
所以长方体被平面AB1EF割成的体积较小部分为三棱台D1EF﹣A1B1A,
设长方体的各棱长为AB=a,AD=b,AA1=c,则长方体的体积为V=abc,
再由棱台体积公式可得
,
较大部分的体积为;
所以体积较大部分与体积较小部分的体积之比为.
故选:C.
3.(2023秋 海门区校级月考)如图,圆锥的轴截面SAB是正三角形,O为底面圆的圆心,D为SO的中点,点C在底面圆的圆周上,且△ABC是等腰直角三角形,则直线CD与AS所成角的余弦值为( )
A. B. C. D.
【解答】解:取OA的中点E,
由D为SO的中点,
则DE∥SA,
则直线CD与AS所成的角为∠CDE(或其补角),
不妨设|AB|=2,
又圆锥的轴截面SAB是正三角形,O为底面圆的圆心,D为SO的中点,点C在底面圆的圆周上,且△ABC是等腰直角三角形,
则|DE|,,,
在△CDE中,由余弦定理可得cos∠CDE,
即直线CD与AS所成角的余弦值为,
故选:C.
4.(2025春 润州区校级期中)下列叙述中,正确的是( )
A.因为P∈α,Q∈α,所以PQ∈α
B.因为P∈α,Q∈β,所以α∩β=PQ
C.因为AB α,C∈AB,D∈AB,所以CD∈α
D.因为AB α,AB β,所以α∩β=AB
【解答】解:因为P∈α,Q∈α,所以PQ α,故A错误;
由P∈α,Q∈β,推不出α∩β=PQ,故B错误;
因为AB α,C∈AB,D∈AB,所以CD α,故C错误;
因为AB α,AB β,所以A∈(α∩β)且B∈(α∩β),故D正确.
故选:D.
5.(2024春 锡山区校级期末)若底面半径为r,母线长为l的圆锥的表面积与直径为l的球的表面积相等,则( )
A. B. C. D.
【解答】解:因为底面半径为r,母线长为l的圆锥的表面积与直径为l的球的表面积相等,
又圆锥的表面积为πrl+πr2,球的表面积为,
所以πrl+πr2=πl2,即,
解得.
故选:B.
6.(2025 姜堰区模拟)在三棱锥S﹣ABC中,底面△ABC为斜边的等腰直角三角形,顶点S在底面ABC上的射影为AC的中点.若SA=2,E为线段AB上的一个动点,则SE+CE的最小值为( )
A. B. C. D.
【解答】解:如图,在三棱锥S﹣ABC中,设点O为线段AC的中点,连接BO,SO,
由题易知:平面ABC,
在Rt△ABC中,,故,
所以△SAB是边长为2的等边三角形,
将△SAB展开到与△ABC共面,如图所示,
则SE+CE≥SC,当且仅当S,E,C三点共线时等号成立,即SE+CE取得最小值,
在△SBC中,,
由余弦定理可得:,
所以,
即SE+CE的最小值为.
故选:A.
7.(2025春 淮安期中)在直三棱柱ABC﹣A1B1C1中,AB⊥AC,AB=AC=1,,则异面直线AC1与BC所成角的余弦值为( )
A. B. C. D.
【解答】解:连接AB1,因为BC∥B1C1,
所以∠B1C1A等于异面直线AC1与BC所成的角,
因为AB⊥AC,AB=AC=1,,所以BC=B1C1,
AC1=AB1,
在△AB1C1中,由余弦定理可得cos∠B1C1A
.
所以异面直线AC1与BC所成角的余弦值为.
故选:C.
8.(2025 江苏校级模拟)如图是一个棱长为2的正方体被过棱A1B1、A1D1的中点M、N,顶点A和过点N顶点D、C1的两个截面截去两个角后所得的几何体,则该几何体的体积为( )
A.5 B.6 C.7 D.8
【解答】解:如图将正方体还原可得如下图形:
则,,
所以该几何体的体积 .
故选:C.
二.多选题(共3小题)
(多选)9.(2025 江苏校级模拟)如图,圆锥的底面直径AB=2,母线VA=3,点C是母线VB的中点.以下结论正确的是( )
A.沿圆锥的侧面从点A到达点C的最短距离为
B.圆锥的外接球表面积为
C.过点C作平行于母线VA的平面,截圆锥所得抛物线的焦准距为3
D.过点V作动直线l,满足与母线VA成角,直线l形成的图形被圆锥底面所在平面截得的图形为椭圆
【解答】解:对于A,沿母线VA展开圆锥侧面如图所示,
因为底面直径AB=2,所以底面圆周长为2π,即展开后扇形弧长为2π,
因为母线VA=3,所以展开后扇形半径为3,则扇形圆心角∠AVA',
所以∠AVB,点A到VB的距离为3sin,
即沿圆锥的侧面从点A到达点C的最短距离为,故A正确;
对于B,由对称性知外接球球心O在圆锥的高上,
设O到底面的距离为d,外接球半径为R,
因为母线长为3,底面半径为1,所以圆锥的高为2,
则R2=12+d2,解得d,R,
则圆锥的外接球表面积等于4πR2,故B正确;
对于C,点C为母线VB中点,过点C与母线VA的平面必过底面圆圆心,交底面圆与E、F,如图,
EF=2,设底面圆圆心为M,则MCVA,
以C为坐标原点,CM所在直线为x轴,在截面内建立平面直角坐标系,
如图,
设抛物线方程为y2=2px,将点E(,1)代入,得p,故焦准距为,C错误;
对于D,由已知圆锥底面与直线VA所成角α满足cosα,动直线l与VA夹角β为,
其形成轨迹为一个圆锥面,VA为该圆锥的轴,l为母线,
因为cosβ,所以α>β,所以直线l形成的图形被圆锥底面所在平面截得的图形为椭圆,D正确.
故选ABD.
(多选)10.(2024秋 鼓楼区校级期末)如图,在正方体ABCD﹣A1B1C1D1中,E为棱B1C1的中点,动点P沿着棱DC从点D向点C移动,对于下列四个结论,正确的是( )
A.存在点P,使得PA1=PE
B.存在点P,使得BD1⊥平面PA1E
C.△PA1E的面积越来越小
D.四面体A1PB1E的体积不变
【解答】解:对于A,设正方体棱长为2,DP=m(0≤m≤2),由AA1⊥平面ABCD,AP 平面ABCD,得AA1⊥AP,
同理PC⊥EC,所以AD2+DP2=8+m2,
PE2=PC2+CE2=(2﹣m)2+5,由8+m2=(2﹣m)2+5,解得,
所以存在P使得PA1=PE,故A正确;
对于B,以D为坐标原点,DA、DC、DD1所在直线分别为x、y、z轴建立空间直角坐标系,如下图,
设正方体棱长为2,则A1(2,0,2),E(1,2,2),B(2,2,0),D1(0,0,2),
所以(﹣1,2,0),,
,所以BD1不可能与A1E垂直,故BD1⊥平面PA1E也不可能成立,故B错误;
对于C,在B中所建空间直角坐标系中,设P(0,m,0)(0≤m≤2),则(1,2﹣m,2),
,,
所以,
设P到直线A1E的距离为d,则d
,
由二次函数性质知0≤m≤2时,y=(m﹣4)2+20递减,所以d递减,
又不变,ΔA1PE的面积为 d,所以ΔA1PE的面积递减,故C正确;
对于D,正方体中,CD∥平面A1B1C1D1,P∈CD,所以P到平面A1B1C1D1的距离不变,
即P到平面A1B1E的距离不变,而ΔA1B1E面积不变,因此三棱锥P=A1B1E即四面体A1PB1E的体积不变,故D正确.
综上,ACD正确.
故选:ACD.
(多选)11.(2025 江苏三模)如图,在边长为12的正方形ABCD中,E1,E2,F1,F2分别边AD,BC的三等分点,正方形内有两点P,Q,点P到AD,CD的距离分别为3a,2a,点Q到BC,AB的距离也是3a和2a,其中0<a<2.将该正方形沿E1F1,E2F2折起,使AB与DC重合,则在该空间图形中,( )
A.直线PQ∥平面E1E2F2F1
B.PQ的最小值为
C.线段PQ的中点到A的距离不超过
D.异面直线PQ与AB成45°角时,
【解答】解:如图,
取E1E2中点O1,F1F2的中点O,连接OB,OO1,
因为BF2=F2F1=F1B=4,所以BO⊥F1F2,
因为E1F1⊥F1B,E1F1⊥F1F2,又F1B∩F1F2,F1B,F1F2 面BF1F2,
所以E1F1⊥面BF1F2,又OO1∥E1F1,所以OO1⊥面BF1F2,
故OB,OF2,OO1两两垂直,建立如图所示的空间直角坐标系,
设QH⊥BF1于H,PM⊥BF2于M,过H作HK⊥OB于K,
易知,BH=2a,又,
所以,
又QH=3a,
所以,同理可知,
所以,
对于选项A,易知平面E1E2F2F1的一个法向量为,
因为,
显然QP 平面E1E2F2F1,所以PQ∥平面E1E2F2F1,故选项A正确;
对于选项B,因为,
令y=40a2﹣144a+144,其中0<a<2,
对称轴,所以,
所以,故选项B正确;
对于选项C,因为PQ的中点,,
所以|AS|3,故选项C错误;
对于选项D,因为,所以,
所以,整理得到2a2﹣9a+9=0,
解得或a=3(舍),故选项D正确.
故选:ABD.
三.填空题(共3小题)
12.(2025 金坛区校级二模)在三棱锥中P﹣ABC,,且AB⊥BC.记直线PA,PC与平面ABC所成角分别为α,β,已知β=2α=60°,当三棱锥P﹣ABC的体积最小时,则三棱锥P﹣ABC外接球的表面积为 16π .
【解答】解:设点P在平面ABC内的投影为P',因为直线PA,PC与平面ABC所成角分别为α,β,且β=2α=60°,则α=30°,
根据线面夹角关系可知,,
所以3|P'C|=|P'A|,
由阿波罗尼斯圆可知,投影P'在圆上运动,以AC所在直线为x轴,过AC的中点O作垂线,建立如图所示直角坐标系,
因为,AB=BC,且AB⊥BC,所以AC,OB=OA=2,
令P'(x,y),由题可知A(﹣2,0),B(0,2),C(2,0),
则,
化简得,
可知P'在以为圆心,半径为的圆上,
当|P'C|最小时,|P'P|最小,即三棱锥P﹣ABC的体积最小,
此时P'(1,0),,,,
∴P点在底面ABC上的射影P'在AC上,且∠APC=90°,又∠ABC=90°,
∴此时三棱锥P﹣ABC的外接球的球心为AC的中点,
外接球的半径,.
故答案为:16π.
13.(2025春 亭湖区校级月考)已知正四棱台的高为3,其顶点都在同一球面上.若该球的半径为5,球心在正四棱台的一个底面上,则该正四棱台的体积为 122 .
【解答】解:因为正四棱台的高为3,其顶点都在同一球面上,
且该球的半径为5,球心在正四棱台的一个底面上,
设球心所在底面为下底面,正四棱台的高为3,球半径为5,
设上底面边长为a,则上底面中心到顶点距离为,
根据勾股定理,即,解得,
因为球心在下底面,下底面中心到顶点距离就是球半径5,
设下底面边长为b,则,解得,
根据正四棱台体积公式(其中h是高,S是下底面积,S′是上底面积),
下底面积,上底面积S′=a2=32,
已知高h=3,则体积.
故答案为:122.
14.(2025春 盐城校级期中)如图,一块矿石晶体的形状为四棱柱ABCD﹣A1B1C1D1,底面ABCD是正方形,CC1=3,CD=3,且∠C1CB=60°,∠C1CD=60°,A1C与AD1所成角的余弦值为 .
【解答】解:分别取,则,
且,
而,
由,
,
,
设A1C与AD1的所成角为θ,
则cosθ=|cos,|.
故答案为:.
四.解答题(共5小题)
15.(2023春 江苏月考)如图,在四棱锥P﹣ABCD中,底面ABCD为平行四边形,E为棱PC的中点,平面ABE与棱PD交于点F.
(1)求证:PA∥平面BDE;
(2)求证:F为PD的中点;
【解答】证明:(1)如图所示:
连接AC交BD于点G,连接GE,
因为ABCD为平行四边形,
所以G为AC的中点,
又E为PC的中点,
所以GE∥PA,
又PA 平面BDE,GE 平面BDE,
所以PA∥平面BDE;
(2)因为底面ABCD为平行四边形,
所以AB∥CD,
又AB 平面ABCD,CD 平面ABCD,
所以CD∥平面ABEF,
又平面ABEF∩平面PDC=EF,
所以CD∥EF,
又因为E为PC的中点,
所以F为PD的中点.
16.(2025春 南京校级期中)如图,在直三棱柱ABC﹣A1B1C1中,所有棱长均为4,D是AB的中点.
(1)求证:BC1∥平面A1DC;
(2)求异面直线A1D与BC1所成角的正弦值.
【解答】(1)证明:连接AC1交A1C于O,
在直三棱柱ABC﹣A1B1C1中,所有棱长均为4,
因此四边形AA1C1C是正方形,所以O是AC1的中点,而D是AB的中点,
因此有OD∥BC1,而OD 平面A1DC,BC1 平面A1DC,
所以BC1∥平面A1DC;
(2)解:由(1)可知:OD∥BC1,
因此异面直线A1D与BC1所成角为∠A1DO(或其补角),
因为AA1C1C是正方形,所以,
在直三棱柱ABC﹣A1B1C1中,所有棱长均为4,
因此四边形BB1C1C是正方形,因此有,
在直三棱柱ABC﹣A1B1C1中,侧棱垂直于底面,因此也就垂直底面中任何直线,
因此有,
由余弦定理可知:,
因此.
17.(2025春 滨湖区校级期中)如图在四棱锥P﹣ABCD中,AB∥CD,M,N分别是PA,BC的中点,CD=3AB.
(1)求证:MN∥平面PCD;
(2)若点F在棱PC上且满足PF=λPC,PA∥平面BDF,求λ的值.
【解答】(1)证明:取PB的中点E,连接ME,EN,
因为AB∥CD,M,N分别是PA,BC的中点,
所以EM∥AB,EN∥PC,
所以ME∥CD,
ME 平面PCD,EN 平面PCD,CD 平面PCD,PC 平面PCD,
所以ME∥平面PCD,EN∥平面PCD,
且ME∩EN=E,
所以平面MEN∥平面PCD,
又因为MN 平面MEN,
所以MN∥平面PCD;
(2)解:连接AC,交BD于O,连接OF,又因为DC=3AB,AB∥CD,
所以AOOC,
因为PA∥平面BDF,PA 平面PAC,
平面PAC∩平面BDF=OF,
所以PA∥OF,
所以,
所以PFFC,可得PFPC,
又因为PF=λPC,
可得λ.
18.(2025春 滨湖区校级期中)现有一几何体由上、下两部分组成,上部是正四棱锥P﹣A1B1C1D1,下部是正四棱柱ABCD﹣A1B1C1D1(如图所示),且正四棱柱的高O1O是正四棱锥的高PO1的4倍.
(1)若AB=6,PO1=2,求该几何体的体积.
(2)若正四棱锥的侧棱长为6,PO1=2.
(i)求正四棱锥P﹣A1B1C1D1的侧面积.
(i)若Q,N分别是线段A1B1,PB1上的动点,求AQ+QN+NC1的最小值.
【解答】解:(1)由条件可知,正四棱柱的高O1O=8,
所以正四棱柱的体积为6×6×8=288,
三棱锥P﹣A1B1C1D1的体积为,
所以该几何体的体积为288+24=312;
(2)(i),
所以,
正四棱锥P﹣A1B1C1D1侧面的高为,
所以正四棱锥的侧面积为;
(ii)如图,将长方形ABB1A1,△PA1B1和△PB1C1展开在一个平面,
PA1=PB1=PC1=6,A1B1=B1C1=8,
设∠A1B1P=α,,A1B1=AA1=8,,
,所以,
所以,
,
,
当A,Q,N,C1四点共线时,AQ+QN+NC1最短,
所以,
所以AQ+QN+NC1的最小值为.
19.(2025春 鼓楼区校级月考)在多面体ABCDPE中(如图),底面ABCD为梯形,AB⊥AD,AB∥CD,F为PA的中点,,,四边形PDCE为矩形,平面PDCE⊥平面ABCD.
(1)求证:平面PBD⊥平面ABCD;
(2)求三棱锥P﹣ABD外接球的体积;
(3)在线段EF上是否存在一点Q,使得BQ与平面PBC所成角的大小为若存在,求出FQ的长;若不存在,请说明理由.
【解答】解:(1)证明:因为四边形PDCE为矩形,
所以PD⊥CD,
因为平面PDCE⊥平面ABCD,
平面PDCE∩平面ABCD=CD,PD 平面PDCE,
所以PD⊥平面ABCD,
又因为PD 平面PBD,
所以平面PBD⊥平面ABCD;
(2)由(1)知PD⊥平面ABCD,
BD 平面ABCD,
所以PD⊥BD,
所以Rt△PBD的外心O在BD的中点,
所以OG∥PD,所以OG⊥平面ABCD,
AB⊥AD,所以Rt△ABD的外心G在BD的中点,
所以点O为三棱锥P﹣ABD外接球的球心,
,,
所以外接球的半径,
则三棱锥P﹣ABD外接球的体积为;
(3)因为AD⊥DC,PD⊥平面ABCD,
所以以D为原点,以DA,DC,DP所在直线为x轴,y轴,z轴建立空间直角坐标系,
则A(1,0,0),,,B(1,1,0),C(0,2,0),,
设线段EF上存在一点Q,使得BQ与平面PBC所成角的大小为,
设Q(x1,y1,z1),,λ∈[0,1],
则.
所以,,,
设平面PBC的法向量为,
则,
取x=1,则y=1,,
则,
因为,
又BQ与平面PBC所成角的大小为,
所以,
即,
整理得λ2=1,所以λ=1,
此时点Q与点E重合,
所以,
则.
综上:在线段EF上存在一点Q,使得BQ与平面PBC所成角的大小为,此时FQ的长度为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
