人教版五年级数学上册《多边形的面积》整理与复习课件(共16张PPT)
文档属性
| 名称 | 人教版五年级数学上册《多边形的面积》整理与复习课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 594.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-25 10:20:13 | ||
图片预览




文档简介
(共16张PPT)
《多边形的面积》
整理与复习
人教版五上第六单元
一、知识回顾
同学们,你们还记得第六单元《多边形的面积》有几个模块的内容吗?
二、知识梳理
1、分工合作,整理模块内容:
1、2组:《平行四边形的面积》;
3、4组:《三角形的面积》;
5、6组:《梯形的面积》;
7、8组:《组合图形的面积》;
9、10组:《估算不规则图形的面积》。
2、展示汇报:
整理完毕后,确定汇报人,依次分组汇报。
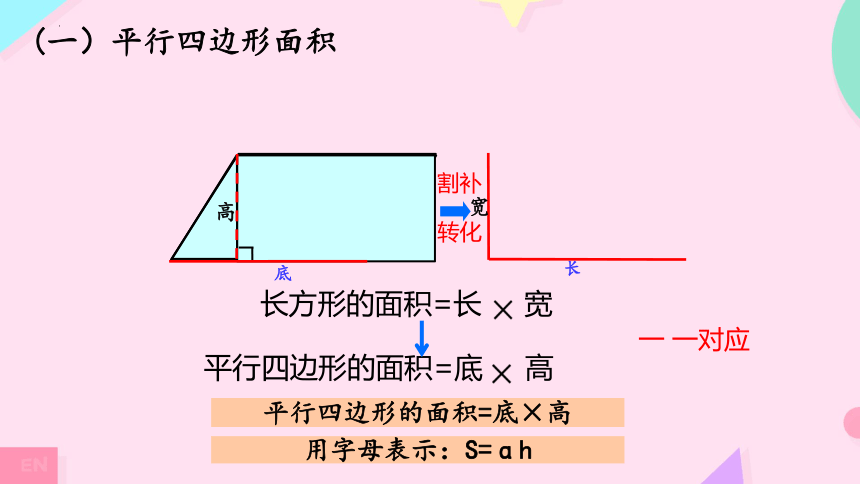
平行四边形的面积=底×高
底
长
高
宽
用字母表示:S=ɑh
(一)平行四边形面积
长方形的面积=长 宽
平行四边形的面积=底 高
割补
转化
一 一对应
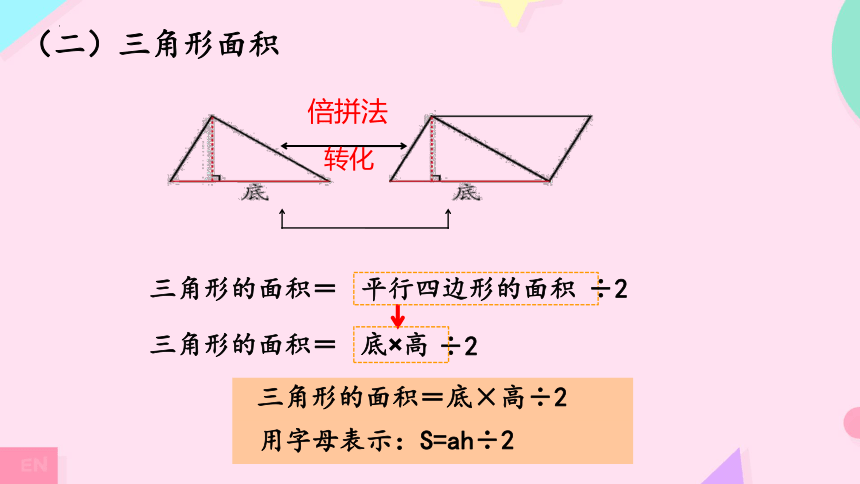
三角形的面积=
用字母表示:S=ah÷2
÷2
平行四边形的面积
÷2
底×高
(二)三角形面积
三角形的面积=底×高÷2
倍拼法
转化
三角形的面积=
大约在2000年前,我国数学名著《九章算术》中的“方田章”就论述了平面图形面积的算法。书中说:“方田术曰,广从(zòng)步数相乘得积步。”其中“方田”是指长方形田地,“广”和“从”是指长和宽,也就是说:长方形面积=长×宽。还说:“圭田术曰,半广以乘正从。”就是说:三角形面积=底×高÷2。
你知道吗
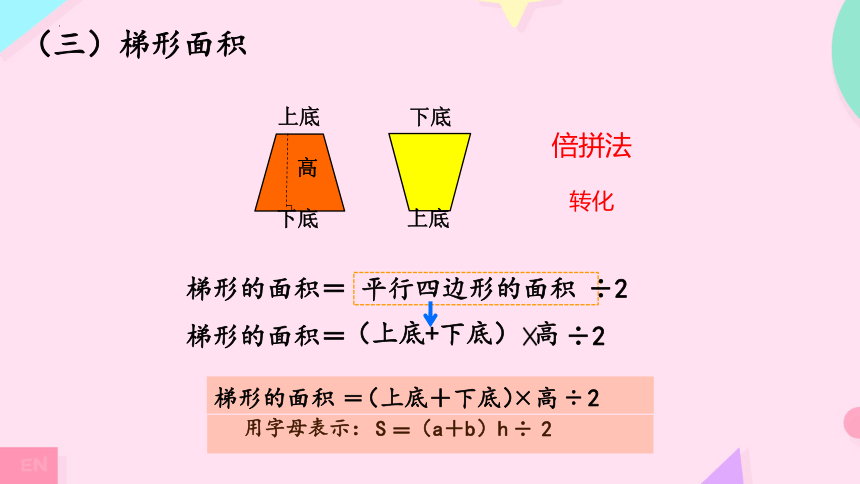
梯形的面积
=
×
高
÷
2
用字母表示:
S
(上底+下底)
=
(a+b)
h
÷
2
上底
下底
上底
下底
高
梯形的面积=
平行四边形的面积
÷2
(上底+下底) 高
÷2
(三)梯形面积
梯形的面积=
倍拼法
转化
10cm
8cm
12cm
分割法:将组合图形分割成两个或两个以上的基本图形的方法。
添补法:通过添加辅助线,将组合图形转化成基本图形的方法。
S组合= S三角形 + S长方形
12×4÷2+12×8 = 120(cm2)
S组合= S大长方形 – S梯形
10×12-(10+4)×(12-8)÷2 = 92(cm2)
10cm
8cm
12cm
4cm
(四)组合图形面积
4cm
(五)估算不规则图形面积
转化
不规则图形
规则图形
在区间范围内,合理即可!
a
a
a
b
a
b
h
h
a
h
S=ah
S=ah÷2
S=(a+b)h÷2
转化
转化
转化
a
b
S=ab
(六)几种图形之间的关系
1、把一个长方形的木条框架拉成一个平行四边形,它的周长和面积都不变。
2、两个面积相等的三角形,形状一定相同。
3、面积相等的两个梯形,一定能拼成一个平行四边形。
4、三角形的面积是和它等底等高的平行四边形面积的一半。
5、两个平行四边形的面积相等,那么它们的底和高都相等。
√
×
×
×
×
(一)看谁最会判
三、知识应用
陶乐园有一块平行四边形菜地(如下图),分成三块种蔬菜。每一种蔬菜各种了多少平方米?
8m
12m
16m
10m
(二)看谁最能干
答:黄瓜、西红柿、茄子分别种了40㎡、120㎡和120㎡。
黄瓜
西红柿
茄子
正方形的周长是20厘米,求正方形和平行四边形的面积?
(三)看谁会思考
在下面的梯形中剪去一个最大的平行四边形,剩下的面积是多少?有几种求法?
方法一:(2+3.5)×1.8÷2-2×1.8=1.35(cm2)
方法二:(3.5-2)×1.8÷2=1.35(cm2)
答:剩下的面积是1.35cm2。有两种求法。
(四)看谁更厉害
2m
3.5m
1.8m
数学思想
转化
数学方法
割补法
应用面积公式解决问题
倍拼法
一一对应
《多边形的面积》
整理与复习
人教版五上第六单元
一、知识回顾
同学们,你们还记得第六单元《多边形的面积》有几个模块的内容吗?
二、知识梳理
1、分工合作,整理模块内容:
1、2组:《平行四边形的面积》;
3、4组:《三角形的面积》;
5、6组:《梯形的面积》;
7、8组:《组合图形的面积》;
9、10组:《估算不规则图形的面积》。
2、展示汇报:
整理完毕后,确定汇报人,依次分组汇报。
平行四边形的面积=底×高
底
长
高
宽
用字母表示:S=ɑh
(一)平行四边形面积
长方形的面积=长 宽
平行四边形的面积=底 高
割补
转化
一 一对应
三角形的面积=
用字母表示:S=ah÷2
÷2
平行四边形的面积
÷2
底×高
(二)三角形面积
三角形的面积=底×高÷2
倍拼法
转化
三角形的面积=
大约在2000年前,我国数学名著《九章算术》中的“方田章”就论述了平面图形面积的算法。书中说:“方田术曰,广从(zòng)步数相乘得积步。”其中“方田”是指长方形田地,“广”和“从”是指长和宽,也就是说:长方形面积=长×宽。还说:“圭田术曰,半广以乘正从。”就是说:三角形面积=底×高÷2。
你知道吗
梯形的面积
=
×
高
÷
2
用字母表示:
S
(上底+下底)
=
(a+b)
h
÷
2
上底
下底
上底
下底
高
梯形的面积=
平行四边形的面积
÷2
(上底+下底) 高
÷2
(三)梯形面积
梯形的面积=
倍拼法
转化
10cm
8cm
12cm
分割法:将组合图形分割成两个或两个以上的基本图形的方法。
添补法:通过添加辅助线,将组合图形转化成基本图形的方法。
S组合= S三角形 + S长方形
12×4÷2+12×8 = 120(cm2)
S组合= S大长方形 – S梯形
10×12-(10+4)×(12-8)÷2 = 92(cm2)
10cm
8cm
12cm
4cm
(四)组合图形面积
4cm
(五)估算不规则图形面积
转化
不规则图形
规则图形
在区间范围内,合理即可!
a
a
a
b
a
b
h
h
a
h
S=ah
S=ah÷2
S=(a+b)h÷2
转化
转化
转化
a
b
S=ab
(六)几种图形之间的关系
1、把一个长方形的木条框架拉成一个平行四边形,它的周长和面积都不变。
2、两个面积相等的三角形,形状一定相同。
3、面积相等的两个梯形,一定能拼成一个平行四边形。
4、三角形的面积是和它等底等高的平行四边形面积的一半。
5、两个平行四边形的面积相等,那么它们的底和高都相等。
√
×
×
×
×
(一)看谁最会判
三、知识应用
陶乐园有一块平行四边形菜地(如下图),分成三块种蔬菜。每一种蔬菜各种了多少平方米?
8m
12m
16m
10m
(二)看谁最能干
答:黄瓜、西红柿、茄子分别种了40㎡、120㎡和120㎡。
黄瓜
西红柿
茄子
正方形的周长是20厘米,求正方形和平行四边形的面积?
(三)看谁会思考
在下面的梯形中剪去一个最大的平行四边形,剩下的面积是多少?有几种求法?
方法一:(2+3.5)×1.8÷2-2×1.8=1.35(cm2)
方法二:(3.5-2)×1.8÷2=1.35(cm2)
答:剩下的面积是1.35cm2。有两种求法。
(四)看谁更厉害
2m
3.5m
1.8m
数学思想
转化
数学方法
割补法
应用面积公式解决问题
倍拼法
一一对应
