19.3正方形与特殊的四边形综合题专训(2)
文档属性
| 名称 | 19.3正方形与特殊的四边形综合题专训(2) |  | |
| 格式 | zip | ||
| 文件大小 | 227.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-14 21:45:58 | ||
图片预览



文档简介
华师大版八年级下册19.3正方形与特殊的四边形综合题专训
正方形与平行四边形综合
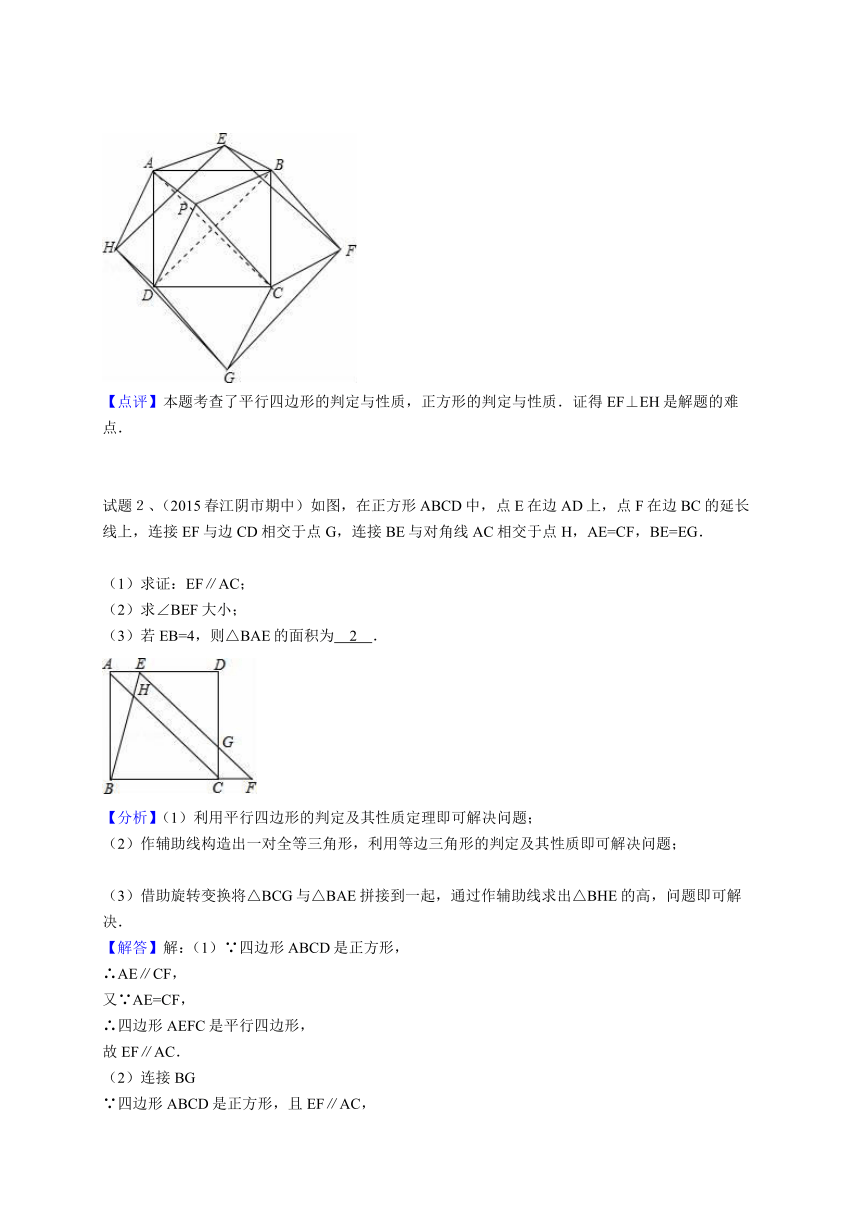
试题1、如图,P是正方形ABCD内一点,以正方形ABCD的一条边做为对角线,点P与这条边的两个端点作平行四边形,依次得点E、F、G、H,求证:四边形EFGH是正方形.
【分析】如图,连接BD、AC.则AC=BD.通过证明△AHE≌△PDB(SAS),推知HE=BD,∠AHE=∠PDB,则HE∥DB.易证四边形EFGH是平行四边形.同理,EF∥HG∥AC,EF=AC=HG,所以EH=EF,EH⊥EF,故四边形EFGH是正方形.
【解答】证明:如图,连接BD、AC.则AC=BD.
∵四边形AHDP和四边形AEBP为平行四边形,
∴AH=DP,AE=BP.
又∵∠HAP+∠APD=180°,∠EAP+∠BPA=180°.
∴∠HAE=∠BPD,
在△AHE与△PDB中,
,
∴△AHE≌△PDB(SAS),
∴HE=BD,∠AHE=∠PDB,
又∵AH∥PD,
∴HE∥DB.
同理,GF=BD,GF∥BD,
∴HE=GF,HE∥GF∥BD,
∴四边形EFGH是平行四边形.
同理,EF∥HG∥AC,EF=AC=HG,
又AC⊥BD,
∴EH=EF,EH⊥EF,
∴四边形EFGH是正方形.
【点评】本题考查了平行四边形的判定与性质,正方形的判定与性质.证得EF⊥EH是解题的难点.
试题2、(2015春江阴市期中)如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连接EF与边CD相交于点G,连接BE与对角线AC相交于点H,AE=CF,BE=EG.
(1)求证:EF∥AC;
(2)求∠BEF大小;
(3)若EB=4,则△BAE的面积为 2 .
【分析】(1)利用平行四边形的判定及其性质定理即可解决问题;
(2)作辅助线构造出一对全等三角形,利用等边三角形的判定及其性质即可解决问题;
(3)借助旋转变换将△BCG与△BAE拼接到一起,通过作辅助线求出△BHE的高,问题即可解决.
【解答】解:(1)∵四边形ABCD是正方形,
∴AE∥CF,
又∵AE=CF,
∴四边形AEFC是平行四边形,
故EF∥AC.
(2)连接BG
∵四边形ABCD是正方形,且EF∥AC,
∴∠DEG=∠DAC=45°,∠DGE=∠DCA=45°;
故∠CFG=∠DEG=45°,∠CGF=∠DGE=45°,
∴∠CGF=∠CFG,CG=CF;
∵AE=CF,
∴AE=CG;
在△ABE与△CBG中,
,
∴△ABE≌CBG(SAS),
∴BE=BG;
又∵BE=EG,
∴BE=BG=EG,△BEG是等边三角形,
故∠BEF=60°.
(3)延长EA到M,使AH=CG;过点M作MK⊥BE于点K;
∵△BEG是等边三角形,
∴∠EBG=60°,
∴∠ABE+∠CBG=90°﹣60°=30°;
在△ABM与△BCG中,
,
∴△ABM≌△BCG(SAS),
∴BM=BC=4,∠ABM=∠CBG;
故∠ABM+∠ABE=∠ABE+∠CBG=30°,
∴MK=,
∴△BME的面积=,△BAE的面积═.
【点评】考查了正方形的性质、全等三角形的判定及其应用问题;解题的关键是通过作辅助线构造出全等三角形,结合等边三角形的判定及其性质来解决问题;对综合运用能力及探究思维能力提出了较高的要求.
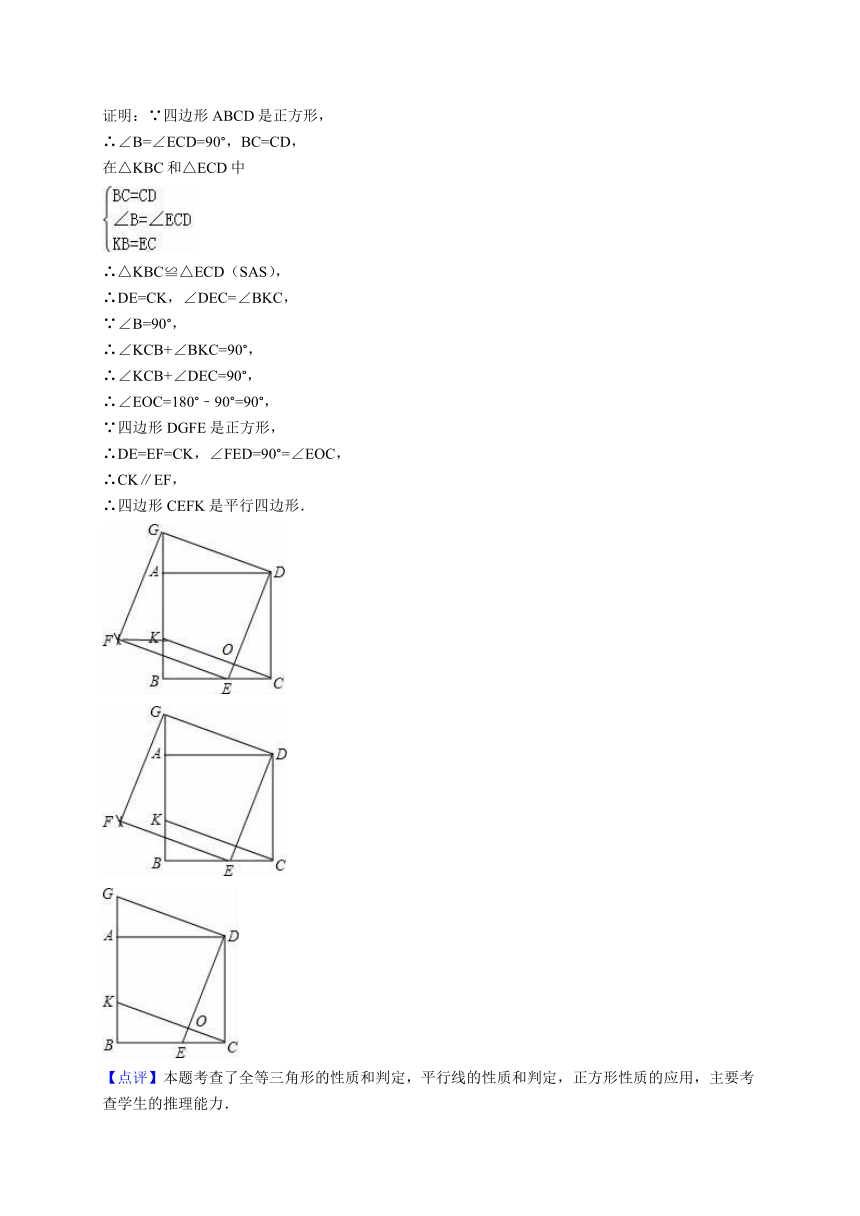
试题3、(2013惠东县校级模拟)如图,四边形ABCD是正方形,点E,K分别在BC,AB上,点G在BA的延长线上,且CE=BK=AG.
(1)求证:①DE=DG;
②DE⊥DG;
(2)尺规作图:以线段DE,DG为边作出正方形DEFG(要求:只保留作图痕迹,不写作法和证明);
(3)连接(2)中的KF,猜想并写出四边形CEFK是怎样的特殊四边形,并证明你的猜想.
【分析】(1)①根据正方形性质求出AD=DC,∠GAD=∠DCE=90°,根据全等三角形判定推出即可;②根据全等得出∠GDA=∠CDE,求出∠GDE=∠GDA+∠ADE=∠ADC=90°即可;
(2)分别以G、E为圆心,以DG为半径画弧,两弧交于F,连接GF、EF即可;
(3)推出EF=CK,EF∥CK,根据平行四边形的判定推出即可.
【解答】(1)①证明:∵四边形ABCD是正方形,
∴AD=DC,∠GAD=∠DCE=90°,
在△GAD和△ECD中
∴△GAD≌△ECD(SAS),
∴DE=DG;
②∵四边形ABCD是正方形,
∴∠ADC=90°,
∵△GAD≌△ECD,
∴∠GDA=∠CDE,
∴∠GDE=∠GDA+∠ADE=∠CDE+∠ADE=∠ADC=90°,
∴DE⊥DG.
(2)解:如图所示:;
(3)四边形CEFK是平行四边形,
证明:∵四边形ABCD是正方形,
∴∠B=∠ECD=90°,BC=CD,
在△KBC和△ECD中
∴△KBC≌△ECD(SAS),
∴DE=CK,∠DEC=∠BKC,
∵∠B=90°,
∴∠KCB+∠BKC=90°,
∴∠KCB+∠DEC=90°,
∴∠EOC=180°﹣90°=90°,
∵四边形DGFE是正方形,
∴DE=EF=CK,∠FED=90°=∠EOC,
∴CK∥EF,
∴四边形CEFK是平行四边形.
【点评】本题考查了全等三角形的性质和判定,平行线的性质和判定,正方形性质的应用,主要考查学生的推理能力.
试题4、(2015春天水期末)如图所示:在△ABC中,分别以AB、AC、BC为边,在BC的同侧作等边△ABD、等边△ACE、等边△BCF.
(1)求证:四边形DAEF是平行四边形;
(2)探究下列问题:(只填条件,不需证明)
①当∠BAC满足 ∠BAC=150° 条件时,四边形DAEF是矩形;
②当∠BAC满足 ∠BAC=60° 条件时,以D、A、E、F为顶点的四边形不存在;
③当△ABC满足 ∠BAC=150°且AB=AC 条件时,四边形DAEF是正方形.
【分析】(1)由等边三角形的性质得出AC=CE=AE,AB=AD=BD,BC=CF=BF,∠BCF=∠ACE=60°,求出∠BCA=∠FCE,证△BCA≌△FCE,得出EF=BA=AD,同理DF=AC=AE,即可得出结论;
(2)①求出∠DAE的度数,根据矩形的判定得出即可;
②证出D、A、E三点共线,即可得出结论;
③由①得出四边形DAEF是矩形;再由AB=AC≠BC得出四边形DAEF是菱形,即可得出结论.
【解答】(1)证明:∵△ABD、△BCE、△ACE是等边三角形,
∴AC=CE=AE,AB=AD=BD,BC=CF=BF,∠BCF=∠ACE=60°,
∴∠BCA=∠FCE=60°﹣∠ACF,
在△BCA和△FCE中,
,
∴△BCA≌△FCE(SAS),
∴EF=BA=AD,
同理:DF=AC=AE,
∴四边形DAEF是平行四边形;
(2)解:①当∠A=150°时,四边形DAEF是矩形,理由如下:
∵△ABD、△ACE是等边三角形,
∴∠DAB=∠EAC=60°,
∴∠DAE=360°﹣60°﹣60°﹣150°=90°,
∵四边形DAEF是平行四边形,
∴四边形DAEF是矩形,
故答案为:=150°;
②当∠BAC=60°时,以D、A、E、F为顶点的四边形不存在;理由如下:
∵∠BAC=60°,∠BAD=∠CAE=60°,
∴点D、A、E共线,
∴以D、A、E、F为顶点的四边形不存在;
故答案为:∠BAC=60°;
③当△ABC满足∠BAC=150°,且AB=AC≠BC时,四边形DAEF是正方形,理由如下:
由①得:当∠BAC=150°时,四边形DAEF是矩形;
当AB=AC时,由(1)得:EF=AB=AD,DF=AC=AE,
∵AB=AC,
∴AD=AE,
∵四边形DAEF是平行四边形,
∴四边形DAEF是菱形,
∴四边形DAEF是正方形.
故答案为:∠BAC=150°,AB=AC.
【点评】本题考查了等边三角形的性质、全等三角形的性质和判定、平行四边形的判定、菱形的判定、矩形的判定以及正方形的判定;解此题的关键是求出EF=BA=AD,DF=AC=AE,主要考查了学生的推理能力.
试题5、(2011嘉兴)以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连接这四个点,得四边形EFGH.
(1)如图1,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;如图2,当四边形ABCD为矩形时,请判断:四边形EFGH的形状(不要求证明);
(2)如图3,当四边形ABCD为一般平行四边形时,设∠ADC=α(0°<α<90°),
①试用含α的代数式表示∠HAE;
②求证:HE=HG;
③四边形EFGH是什么四边形?并说明理由.
【分析】(1)根据等腰直角三角形的性质得到∠E=∠F=∠G=∠H=90°,求出四边形是矩形,根据勾股定理求出AH=HD=AD,DG=GC=CD,CF=BF=BC,AE=BE=AB,推出EF=FG=GH=EH,根据正方形的判定推出四边形EFGH是正方形即可;
(2)①根据平行四边形的性质得出,∠BAD=180°﹣α,根据△HAD和△EAB是等腰直角三角形,得到∠HAD=∠EAB=45°,求出∠HAE即可;
②根据△AEB和△DGC是等腰直角三角形,得出AE=AB,DG=CD,平行四边形的性质得出AB=CD,求出∠HDG=90°+a=∠HAE,根据SAS证△HAE≌△HDG,根据全等三角形的性质即可得出HE=HG;
③与②证明过程类似求出GH=GF,FG=FE,推出GH=GF=EF=HE,得出菱形EFGH,证△HAE≌△HDG,求出∠AHD=90°,∠EHG=90°,即可推出结论.
【解答】(1)解:四边形EFGH的形状是正方形.
(2)解:①∠HAE=90°+α,
在平行四边形ABCD中AB∥CD,
∴∠BAD=180°﹣∠ADC=180°﹣α,
∵△HAD和△EAB是等腰直角三角形,
∴∠HAD=∠EAB=45°,
∴∠HAE=360°﹣∠HAD﹣∠EAB﹣∠BAD=360°﹣45°﹣45°﹣(180°﹣a)=90°+α,
答:用含α的代数式表示∠HAE是90°+α.
②证明:∵△AEB和△DGC是等腰直角三角形,
∴AE=AB,DG=CD,
在平行四边形ABCD中,AB=CD,
∴AE=DG,
∵△AHD和△DGC是等腰直角三角形,
∴∠HDA=∠CDG=45°,
∴∠HDG=∠HDA+∠ADC+∠CDG=90°+α=∠HAE,
∵△AHD是等腰直角三角形,
∴HA=HD,
∴△HAE≌△HDG,
∴HE=HG.
③答:四边形EFGH是正方形,
理由是:由②同理可得:GH=GF,FG=FE,
∵HE=HG,
∴GH=GF=EF=HE,
∴四边形EFGH是菱形,
∵△HAE≌△HDG,
∴∠DHG=∠AHE,
∵∠AHD=∠AHG+∠DHG=90°,
∴∠EHG=∠AHG+∠AHE=90°,
∴四边形EFGH是正方形.
【点评】本题主要考查对正方形的判定,等腰直角三角形的性质,菱形的判定和性质,全等三角形的性质和判定,平行线的性质等知识点的理解和掌握,综合运用性质进行推理是解此题的关键.
正方形与矩形综合
试题1、(2013海安县校级模拟)正方形ABCD,矩形EFGH均位于第一象限内,它们的边平行于x轴或y轴,其中,点A,E在直线OM上,点C,G在直线ON上,O为坐标原点,点A的坐标为(3,3),正方形ABCD的边长为1.若矩形EFGH的周长为10,面积为6,则点F的坐标为 (7,5),(8,5) .
【分析】由A的坐标为(3,3),正方形ABCD的边长为1得出直线OM的解析式,再求出C点的坐标利用待定系数法求出直线ON的解析式;设矩形EFGH的宽为a,则长为5﹣a,再根据面积为6即可得出a的值,由点E在直线OM上设点E的坐标为(e,e),由矩形的边长可用e表示出F、G点的坐标,再根据G点在直线ON上得出e的值,即可得出结论.
【解答】解:∵A的坐标为(3,3),
∴直线OM的解析式为y=x,
∵正方形ABCD的边长为1,
∴C(4,2),
设直线ON的解析式为y=kx(k≠0),
∴2=4k,
解得k=,
∴直线ON的解析式为:y=x;
设矩形EFGH的宽为a,则长为5﹣a,
∵矩形EFGH的面积为6,
∴a(5﹣a)=6,
解得:a=2或a=3,
当a=2即EF=2时,EH=5﹣2=3,
∵点E在直线OM上,设点E的坐标为(e,e),
∴F(e,e﹣2),G(e+3,e﹣2),
∵点G在直线ON上,
∴e﹣2=(e+3),
解得:e=7,
∴F(7,5);
当a=3即EF=3时,EH=5﹣3=2,
∵点E在直线OM上,设点E的坐标为(e,e),
∴F(e,e﹣3),G(e+2,e﹣3),
∵点G在直线ON上,
∴e﹣3=(e+2),
解得:e=8,
∴F(8,5).
故答案为:(7,5),(8,5).
【点评】本题考查了正方形的性质、矩形的性质、一次函数解析式的求法;根据题意得出直线ON的解析式是解答此题的关键,在解答时要注意进行分类讨论.
试题2、(2016春江阴市月考)如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.
(1)求证:HF=AP;
(2)若正方形ABCD的边长为12,AP=4,求线段AF的长.
【分析】(1)由正方形的性质和已知条件可分别证明∠FEH=∠PBA,AB=HE,进而可证明△ABP≌△HEF,由全等三角形的性质即可得到HF=AP;
(2)连接,设AF=x,则PF=BF=12﹣x,在△APF中利用勾股定理可得:42+x2=(12﹣x)2,解方程求出x的值即可.
【解答】解:(1)∵EF⊥BP,EH⊥AB,
∴∠FEH+∠EMQ=90°=∠PBA+∠BMH,
又∵∠QME=∠BMH,
∴∠FEH=∠PBA,
∵四边形ABCD是正方形,
∴∠A=∠D=90°,AB=AD,
∵EH⊥AB,
∴∠EHA=90°=∠A=∠D,
∴四边形ADEH是矩形,
∴AD=EH,
又∵AB=AD,
∴AB=EH,
在△ABP与△HEF中
,
∴△ABP≌△HEF(ASA),
∴AP=FH;
(2)连结PF,
∵EF垂直平分BP,
∴PF=BF,
设AF=x,则PF=BF=12﹣x,
∴在△APF中,42+x2=(12﹣x)2,
∴x=,
∴AF=.
【点评】本题考查的是正方形的性质、勾股定理的运用、全等三角形的判定和性质以及线段垂直平分线的性质,熟知正方形的性质及全等三角形的判定与性质是解答此题的关键.
试题3、(2015春霸州市期末)如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.
(1)试说明EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论.
【分析】(1)根据CE平分∠ACB,MN∥BC,找到相等的角,即∠OEC=∠ECB,再根据等边对等角得OE=OC,同理OC=OF,可得EO=FO.
(2)利用矩形的判定解答,即有一个内角是直角的平行四边形是矩形.
(3)利用已知条件及正方形的性质解答.
【解答】解:(1)∵CE平分∠ACB,
∴∠ACE=∠BCE,
∵MN∥BC,
∴∠OEC=∠ECB,
∴∠OEC=∠OCE,
∴OE=OC,
同理,OC=OF,
∴OE=OF.
(2)当点O运动到AC中点处时,四边形AECF是矩形.
如图AO=CO,EO=FO,
∴四边形AECF为平行四边形,
∵CE平分∠ACB,
∴∠ACE=∠ACB,
同理,∠ACF=∠ACG,
∴∠ECF=∠ACE+∠ACF=(∠ACB+∠ACG)=×180°=90°,
∴四边形AECF是矩形.
(3)△ABC是直角三角形
∵四边形AECF是正方形,
∴AC⊥EN,故∠AOM=90°,
∵MN∥BC,
∴∠BCA=∠AOM,
∴∠BCA=90°,
∴△ABC是直角三角形.
【点评】本题主要考查利用平行线的性质“等角对等边”证明出结论(1),再利用结论(1)和矩形的判定证明结论(2),再对(3)进行判断.解答时不仅要注意用到前一问题的结论,更要注意前一问题为下一问题提供思路,有相似的思考方法.是矩形的判定和正方形的性质等的综合运用.
试题4、(2015春万州区期末)如图,在正方形ABCD中,点E、F、G、H分别在四边上,EH∥BC,GF∥AB,EH与FG交于点O,且AE=AG,若AE比CH长2,△BOF的面积为
(1)求正方形ABCD的面积;
(2)设AE=a,BE=b,求代数式a4+b4的值.
【分析】(1)根据四边形ABCD是正方形,得到AD∥BC,AD=BC,AB∥CD,AB=CD,由于EH∥BC,GF∥AB,得出四边形AEOG是正方形,四边形AEHD,EBFO,GOHD是矩形,根据△BOF的面积为,得到矩形EBFO的面积=3,设AE=OE=DH=x,BE=CH=y,列出,即可得到结果;
(2)由(1)求得AE=3,BE=1,代入即可得到结果.
【解答】解:(1)∵四边形ABCD是正方形,
∴AD∥BC,AD=BC,AB∥CD,AB=CD,
∵EH∥BC,GF∥AB,
∴四边形AEOG是正方形,四边形AEHD,EBFO,GOHD是矩形,
∴AE=DH,BE=CH,
∵△BOF的面积为,
∴矩形EBFO的面积=3,
设AE=OE=DH=x,BE=CH=y,
∴,
∴,
∴AEE=3,BE=1,
∴AB=AE+BE=4,
∴正方形ABCD的面积=4×4=16;
(2)由(1)求得AE=3,BE=1,
∴a=3,b=1,
∴a4+b4=34+11=82.
【点评】本题考查了正方形的判定和性质,正方形的面积,三角形的面积,充分利用已知条件列方程组求出各线段是解题的关键.
试题5、(2015春冷水江市校级期末)如图,矩形ABCD和正方形ECGF.其中E、H分别为AD、BC中点.连结AF、HG、AH.
(1)求证:AF=HG;
(2)求证:∠FAD=∠GHC;
(3)试探究∠FAH与∠AFE的关系.
【分析】(1)根据矩形的性质和已知得出AE=HC,AE∥HC,求出四边形AHCE为平行四边形,根据平行四边形的性质得出AH=EC,AH∥EC,求出四边形AHGF是平行四边形,即可得出答案;
(2)根据平行线得出∠FAH+∠AHG=180°,求出∠DAH=∠AHB,根据∠AHB+∠AHG+∠GHC=180°即可得出答案;
(3)过A点作AM∥EF,根据平行线的性质得出∠MAF=∠AFE,求出MA⊥AH,根据垂直得出∠MAF+∠FAH=90°,即可得出答案.
【解答】(1)证明:∵四边形ABCD是矩形,且E、H分别为AD、BC的中点,
∴AE=HC,AE∥HC,
∴四边形AHCE为平行四边形,
∴AH=EC,AH∥EC,
又∵四边形ECGF为正方形,
∴EC=FG,EC∥FG,
∴AH=FG,AH∥FG,
∴四边形AHGF是平行四边形,
∴AH=FG;
(2)证明:∵四边形AHGF是平行四边形,
∴∠FAH+∠AHG=180°,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAH=∠AHB,
又∵∠AHB+∠AHG+∠GHC=180°,
∴∠FAD=∠GHC;
(3)∠FAH+∠AFE=90°,
证明:过A点作AM∥EF,
则∠MAF=∠AFE,
∵AM∥EF,AH∥EC,FE⊥EC,
∴MA⊥AH,
∴∠MAF+∠FAH=90°,
∴∠FAH+∠MAF=90°.
【点评】本题考查了矩形的性质,平行四边形的性质和判定,正方形的性质的应用,能综合运用知识点进行推理是解此题的关键.
正方形与菱形综合
试题1、(2012深圳模拟)如图,正方形ABCD的边长为2,以对角线BD为边作菱形BEFD,点C、E、F在同一直线上.
(1)求∠EBC的度数;
(2)求CE的长.
【分析】(1)首先连接AC交BD于点O,过点E作EH⊥BD于点H,由正方形ABCD的边长为2,四边形BEFD是菱形,易求得BE=BD=2,由BD∥EF,可求得EH=OC=,然后由三角函数的性质,求得∠EBC的度数;
(2)首先过点E作EG⊥BC,交BC的延长线于点G,即可得△ECG是等腰直角三角形,然后设EG=CG=x,在Rt△BEG中,由BE2=BG2+EG2,可得方程:(2)2=(2+x)2+x2,解此方程即可求得EG的长,继而求得CE的长.
【解答】解:(1)连接AC交BD于点O,过点E作EH⊥BD于点H,
∵正方形ABCD的边长为2,
∴BD=AC=2,AC⊥BD,
∴OC=AC=,
∵四边形BEFD是菱形,
∴BE=BD=2,BD∥EF,
∵点C、E、F在同一直线上,
∴EH=OC=,
在Rt△BEH中,sin∠EBH===,
∴∠EBH=30°,
∴∠EBC=∠DBC﹣∠EBH=45°﹣30°=15°;
(2)过点E作EG⊥BC,交BC的延长线于点G,
∵BD∥EF,
∴∠ECG=∠DBC=45°,
∴△ECG是等腰直角三角形,
∴EG=CG,
设EG=x,
则BG=BC+CG=2+x,
在Rt△BEG中,BE2=BG2+EG2,
即(2)2=(2+x)2+x2,
即2x2+4x﹣4=0,
解得:x=﹣1或x=﹣﹣1(舍去),
∴EG=﹣1,
∴CE=EG=(﹣1)=﹣.
【点评】此题考查了正方形的性质、菱形的性质、特殊角的三角函数值以及勾股定理的知识.此题难度较大,注意掌握辅助线的作法,注意数形结合与方程思想的应用.
试题2、(2013春莒南县期末)如图,正方形ABCD的边长为2,以对角线AC为一边作菱形AEFC,AF于BC交于G点,则∠BCE的度数与BE的长分别为( )
A.30°、
B.30°、
C.22.5°、
D.22.5°、
【分析】根据正方形的对角线平分一组对角可得∠BAC=∠ACB=45°,根据菱形的四条边都相等可得AC=AE,然后根据等腰三角形两底角相等求出∠ACE,然后根据∠BCE=∠ACE﹣∠ACB计算即可得解;再根据正方形的对角线等于边长的倍求出AE=AC,然后根据BE=AE﹣AB计算即可得解.
【解答】解:在正方形ABCD中,∠BAC=∠ACB=45°,
∵四边形AEFC是菱形,
∴AC=AE,
∴∠ACE=(180°﹣∠BAC)=(180°﹣45°)=67.5°,
∴∠BCE=∠ACE﹣∠ACB=67.5°﹣45°=22.5°,
∵正方形ABCD的边长为2,
∴AE=AC=2,
∴BE=AE﹣AB=2﹣2.
故选C.
【点评】本题考查了正方形的性质,菱形的性质,等边对等角的性质,熟记两图形的性质并准确识图是解题的关键.
试题3、(2015春遂宁期末)如图,正方形ABCD的对角线AC是菱形AEFC的一边,则∠FAB的度数为 22.5° .
【分析】根据正方形的性质求出∠BAC=45°,再根据菱形的对角线平分一组对角解答即可.
【解答】解:∵四边形ABCD是正方形,
∴∠BAC=45°,
∵四边形AEFC是菱形,
∴∠FAB=∠BAC=×45°=22.5°.
故答案为:22.5°.
【点评】本题考查了正方形的对角线平分一组对角,菱形的对角线平分一组对角的性质,熟记性质是解题的关键.
试题4、(2014重庆校级二模)如图,已知正方形ABCD的边长为3,菱形EFGH的三个顶点E、G、H分别落在正方形的边AB、CD、DA上,AH=1,则GC长度的取值范围是 3﹣≤GC≤3 .
【分析】由菱形边长来确定GC长度的取值范围.
【解答】解:∵AH=1,
∴HE的最大值为==,
此时DG==,
∴此时GC=3﹣,
当G与点D重合时,菱形的边最小,
∴3﹣≤GC≤3.
故答案为:3﹣≤GC≤3.
【点评】本题主要考查了正方形的性质及菱形的性质,解题的关键是由菱形边长来确定GC长度的取值范围.
试题5、(2014春椒江区校级期中)如图,ABCD是正方形,E是CF上一点,若DBEF是菱形,则∠EBC= 15° .
【分析】过D作DG垂直于CF,垂足为G,由正方形的性质可得出正方形的四条边相等,且四个角为直角,三角形BCD为等腰直角三角形,可得出∠BDC与∠DBC都为45°,设正方形的边长为1,根据勾股定理求出BD的长为,即菱形的四条边为,由DG与FC垂直,且BD与EF平行,可得BD垂直于DG,进而得到∠CDG为45°,即三角形DCG为等腰直角三角形,由DC的长为1,可求出DG为,在直角三角形DFG中,由DG为DF的一半,得到∠F为30°,再根据菱形的对角相等,可得∠DBE为30°,由∠EBC=∠DBC﹣∠DBE求出度数即可.
【解答】解:过D作DG⊥CF,垂足为G,如图所示:
∵四边形ABCD为正方形,
∴∠CBD=∠CDB=45°,∠BCD=90°,
设正方形ABCD的边长为1,即AB=BC=CD=AD=1,
∴根据勾股定理得:BD==,
∵四边形BEFD为菱形,
∴BE=EF=DF=BD=,
又∵BD∥EF,DG⊥FC,
∴BD⊥DG,即∠BDG=90°,
∴∠CDG=∠BDG﹣∠BDC=90°﹣45°=45°,又∠DGC=90°,
∴△DCG为等腰直角三角形,又DC=1,
∴DG=DCsin45°=,又DF=,
在Rt△DFG中,由DG=DF,
∴∠F=30°,
∴∠DBE=30°,
则∠EBC=∠DBC﹣∠DBE=45°﹣30°=15°.
故答案是:15°.
【点评】此题考查了正方形的性质,菱形的性质,等腰直角三角形的性质以及直角三角形的性质,根据题意作出辅助线DG是本题的突破点,熟练掌握图形的性质是解本题的关键.
试题6、(2015荆州)如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
【分析】(1)先证出△ABP≌△CBP,得PA=PC,由于PA=PE,得PC=PE;
(2)由△ABP≌△CBP,得∠BAP=∠BCP,进而得∠DAP=∠DCP,由PA=PC,得到∠DAP=∠E,∠DCP=∠E,最后∠CPF=∠EDF=90°得到结论;
(3)借助(1)和(2)的证明方法容易证明结论.
【解答】(1)证明:在正方形ABCD中,AB=BC,
∠ABP=∠CBP=45°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PE,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPF=∠EDF=90°;
(3)在菱形ABCD中,AB=BC,∠ABP=∠CBP=60°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,
∵PA=PE,
∴PC=PE,
∴∠DAP=∠DCP,
∵PA=PC,
∴∠DAP=∠AEP,
∴∠DCP=∠AEP
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠AEP,
即∠CPF=∠EDF=180°﹣∠ADC=180°﹣120°=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴AP=CE.
【点评】本题考查了正方形的性质,全等三角形的判定与性质,菱形的性质,等边对等角的性质,熟记正方形的性质确定出∠ABP=∠CBP是解题的关键.
正方形与正方形综合
试题1、(2016贵阳模拟)将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
A.2cm2
B.4cm2
C.6cm2
D.8cm2
【分析】连接AP、AN,点A是正方形的对角线的交点,则AP=AN,∠APF=∠ANE=45°,易得PAF≌△NAE,进而可得四边形AENF的面积等于△NAP的面积,同理可得答案.
【解答】解:如图,连接AP,AN,点A是正方形的对角线的交
则AP=AN,∠APF=∠ANE=45°,
∵∠PAF+∠FAN=∠FAN+∠NAE=90°,
∴∠PAF=∠NAE,
∴△PAF≌△NAE,
∴四边形AENF的面积等于△NAP的面积,
而△NAP的面积是正方形的面积的,而正方形的面积为4,
∴四边形AENF的面积为1cm2,四块阴影面积的和为4cm2.
故选B.
【点评】本题考查旋转的性质.旋转变化前后,对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等.要注意旋转的三要素:①定点﹣旋转中心;②旋转方向;③旋转角度.
试题2、现有一张边长等于a(a>16)的正方形纸片,从距离正方形的四个顶点8cm处,沿45°角画线,将正方形纸片分成5部分,则阴影部分是 正方形 (填写图形的形状)(如图),它的一边长是 cm .
【分析】延长小正方形的一边交大正方形于一点,连接此点与距大正方形顶点8cm处的点,构造直角边长为8的等腰直角三角形,将小正方形的边长转化为等腰直角三角形的斜边长来求解即可.
【解答】解:如图,作AB平行于小正方形的一边,延长小正方形的另一边与大正方形的一边交于B点,
∴△ABC为直角边长为8cm的等腰直角三角形,
∴AB=AC=8,
∴阴影正方形的边长=AB=8
cm.
故答案为:正方形,
cm.
【点评】本题考查了正方形的性质与勾股定理的知识,题目同时也渗透了转化思想
试题3、已知,正方形CEFG的边GC在正方形ABCD的边CD上,延长CD到H,使DH=CE,K在BC边上,且BK=CE,求证:四边形AKFH为正方形.
【分析】根据正方形的性质得出AB=BC=CD=AD,∠BAD=∠DCB=∠B=∠ADC=90°,∠GCE=∠E=∠GFE=∠CGF=90°,求出∠ADH=∠HGF=∠E=∠B=90°,BK=GF=DH=EF,KE=GH=AB=AD,证△ABK≌△KEF≌△HGF≌△ADH,根据全等三角形的性质推出AK=KF=HF=AH,∠BAK=HAD,求出∠HAK=∠BAD=90°,根据正方形的判定得出即可.
【解答】证明:∵四边形ABCD和四边形CEFG是正方形,
∴AB=BC=CD=AD,∠BAD=∠DCB=∠B=∠ADC=90°,∠GCE=∠E=∠GFE=∠CGF=90°,
∴∠ADH=∠HGF=∠E=∠B=90°,
∵DH=CE,BK=CE,
∴BK=GF=DH=EF,KE=GH=AB=AD,
在△ABK、△KEF、△HGF、△ADH中
∴△ABK≌△KEF≌△HGF≌△ADH,
∴AK=KF=HF=AH,∠BAK=HAD,
∵∠BAD=90°,
∴∠HAK=∠HAD+∠DAK=∠BAK+∠DAK=∠BAD=90°,
∴四边形AKFH为正方形.
【点评】本题考查了正方形的性质和判定,全等三角形的性质和判定的应用,解此题的关键是推出△ABK≌△KEF≌△HGF≌△ADH,注意:有一个角是直角的菱形是正方形.
试题5、(2013历城区一模)如图,四边形ABCD、DEFG都是正方形,连接AE、CG,AE与CG相交于点M.下列结论:①AE=CG,②AE⊥CG,③DM∥GE,④OM=OD,⑤∠DME=45°.正确结论的个数为( )
A.2个
B.3个
C.4个
D.5个
【分析】根据正方形的性质可得AD=CD,DE=DG,∠ADC=∠EDG=90°,然后求出∠ADE=∠CDG,再利用“边角边”证明△ADE和△CDF全等,根据全等三角形对应边相等可得AE=CG,判定①正确;根据全等三角形对应角相等可得∠1=∠2,再求出∠MEG+∠MGE=∠DEG+∠DGE=90°,然后求出∠EMG=90°,判定②正确;根据直角三角形斜边上的中线等于斜边的一半可得OM=OD=GE,判定④正确;求出点D、E、G、M四点共圆,再根据同弧所对的圆周角相等可得∠DME=∠DGE=45°,判定⑤正确;根据∠MGE≠45°可得∠DME≠∠MGE,判定DM∥GE错误.
【解答】解:∵四边形ABCD、DEFG都是正方形,
∴AD=CD,DE=DG,∠ADC=∠EDG=90°,
∴∠ADC+∠ADG=∠EDG+∠ADG,
即∠ADE=∠CDG,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(SAS),
∴AE=CG,故①正确;
∠1=∠2,
∵∠MEG+∠MGE=∠MEG+∠DGE+∠1=∠MEG+∠2+∠DGE=∠DEG+∠DGE=45°+45°=90°,
∴∠EMG=180°﹣(∠MEG+∠MGE)=180°﹣90°=90°,
∴AE⊥CG,故②正确;
∵O是正方形DEFG的对角线的交点,
∴OE=OG,
∴OM=OD=GE,故④正确;
∵∠EMG=∠EDG=90°,
∴点D、E、G、M四点共圆,
∴∠DME=∠DGE=45°,故⑤正确;
⑤方法二:过D作DP⊥EM于P,DQ⊥CG于Q,
在△GQD与△EPD中,,
∴△GQD≌△EPD,
∴DQ=DP,
∴MD是∠CME的平分线,
∴∠DME=∠CME=45°,故⑤正确;
∵∠MGE≠∠DEG=45°,
∴∠DME≠∠MGE,
∴DM∥GE不成立,故③错误;
综上所述,正确的有①②④⑤共4个.
故选C.
【点评】本题考查了正方形的性质,全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,以及四点共圆,熟练掌握各性质是解题的关键.
试题6、(2014万州区校级模拟)如图,正方形ABCD绕B点逆时针旋转得到正方形BPQR,连接DQ,延长CP交DQ于E.若CE=5,ED=4,则AB= .
【分析】设AD与PQ相交于点O,连接BO,过点C作CM⊥DQ角QD的延长线于M,利用“HL”证明Rt△AOB和Rt△POB全等,根据全等三角形对应边相等可得∠ABO=∠PBO,全等三角形对应边相等可得AO=PO,然后求出OD=OQ,根据等边对等角可得∠ODQ=∠OQD,再根据三角形的内角和定理和四边形的内角和定理求出∠PBO=∠ODQ,再根据等腰三角形两底角相等的性质用∠POB表示出∠PCB,然后求出∠EDB=∠PCB,根据三角形的内角和定理可得∠CED=∠CBD=45°,判断出△CEM是等腰直角三角形,根据等腰直角三角形的性质求出CM=EM=5,再求出DM,然后利用勾股定理列式计算即可求出CD的长,根据正方形的四条边都相等即可得解.
【解答】解:如图,设AD与PQ相交于点O,连接BO,过点C作CM⊥DQ角QD的延长线于M,
在Rt△AOB和Rt△POB中,
,
∴Rt△AOB≌Rt△POB(HL),
∴∠ABO=∠PBO,AO=PO,
∴AD﹣AO=PQ﹣PO,
即OD=OQ,
∴∠ODQ=∠OQD,
∵∠PBO=(360°﹣90°×2﹣∠AOP)=(180°﹣∠AOP),
∠ODQ=(180°﹣∠DOQ),
∠AOP=∠DOQ(对顶角相等),
∴∠PBO=∠ODQ,
∵BC=BP,
∴∠PCB=(180°﹣∠PBC)=(180°﹣90°+2∠POB)=45°+∠PBO,
∠EDB=∠ODQ+∠ADB=∠PBO+45°,
∴∠EDB=∠PCB,
∴∠CED=∠CBD=45°,
∴△CEM是等腰直角三角形,
∵CE=5,
∴CM=EM=5,
∴DM=EM﹣ED=5﹣4=1,
在Rt△CDM中,CD===,
∴AB=CD=.
故答案为:.
【点评】本题考查了正方形的性质,全等三角形的判定与性质,三角形的内角和定理,
正方形与平行四边形综合
试题1、如图,P是正方形ABCD内一点,以正方形ABCD的一条边做为对角线,点P与这条边的两个端点作平行四边形,依次得点E、F、G、H,求证:四边形EFGH是正方形.
【分析】如图,连接BD、AC.则AC=BD.通过证明△AHE≌△PDB(SAS),推知HE=BD,∠AHE=∠PDB,则HE∥DB.易证四边形EFGH是平行四边形.同理,EF∥HG∥AC,EF=AC=HG,所以EH=EF,EH⊥EF,故四边形EFGH是正方形.
【解答】证明:如图,连接BD、AC.则AC=BD.
∵四边形AHDP和四边形AEBP为平行四边形,
∴AH=DP,AE=BP.
又∵∠HAP+∠APD=180°,∠EAP+∠BPA=180°.
∴∠HAE=∠BPD,
在△AHE与△PDB中,
,
∴△AHE≌△PDB(SAS),
∴HE=BD,∠AHE=∠PDB,
又∵AH∥PD,
∴HE∥DB.
同理,GF=BD,GF∥BD,
∴HE=GF,HE∥GF∥BD,
∴四边形EFGH是平行四边形.
同理,EF∥HG∥AC,EF=AC=HG,
又AC⊥BD,
∴EH=EF,EH⊥EF,
∴四边形EFGH是正方形.
【点评】本题考查了平行四边形的判定与性质,正方形的判定与性质.证得EF⊥EH是解题的难点.
试题2、(2015春江阴市期中)如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连接EF与边CD相交于点G,连接BE与对角线AC相交于点H,AE=CF,BE=EG.
(1)求证:EF∥AC;
(2)求∠BEF大小;
(3)若EB=4,则△BAE的面积为 2 .
【分析】(1)利用平行四边形的判定及其性质定理即可解决问题;
(2)作辅助线构造出一对全等三角形,利用等边三角形的判定及其性质即可解决问题;
(3)借助旋转变换将△BCG与△BAE拼接到一起,通过作辅助线求出△BHE的高,问题即可解决.
【解答】解:(1)∵四边形ABCD是正方形,
∴AE∥CF,
又∵AE=CF,
∴四边形AEFC是平行四边形,
故EF∥AC.
(2)连接BG
∵四边形ABCD是正方形,且EF∥AC,
∴∠DEG=∠DAC=45°,∠DGE=∠DCA=45°;
故∠CFG=∠DEG=45°,∠CGF=∠DGE=45°,
∴∠CGF=∠CFG,CG=CF;
∵AE=CF,
∴AE=CG;
在△ABE与△CBG中,
,
∴△ABE≌CBG(SAS),
∴BE=BG;
又∵BE=EG,
∴BE=BG=EG,△BEG是等边三角形,
故∠BEF=60°.
(3)延长EA到M,使AH=CG;过点M作MK⊥BE于点K;
∵△BEG是等边三角形,
∴∠EBG=60°,
∴∠ABE+∠CBG=90°﹣60°=30°;
在△ABM与△BCG中,
,
∴△ABM≌△BCG(SAS),
∴BM=BC=4,∠ABM=∠CBG;
故∠ABM+∠ABE=∠ABE+∠CBG=30°,
∴MK=,
∴△BME的面积=,△BAE的面积═.
【点评】考查了正方形的性质、全等三角形的判定及其应用问题;解题的关键是通过作辅助线构造出全等三角形,结合等边三角形的判定及其性质来解决问题;对综合运用能力及探究思维能力提出了较高的要求.
试题3、(2013惠东县校级模拟)如图,四边形ABCD是正方形,点E,K分别在BC,AB上,点G在BA的延长线上,且CE=BK=AG.
(1)求证:①DE=DG;
②DE⊥DG;
(2)尺规作图:以线段DE,DG为边作出正方形DEFG(要求:只保留作图痕迹,不写作法和证明);
(3)连接(2)中的KF,猜想并写出四边形CEFK是怎样的特殊四边形,并证明你的猜想.
【分析】(1)①根据正方形性质求出AD=DC,∠GAD=∠DCE=90°,根据全等三角形判定推出即可;②根据全等得出∠GDA=∠CDE,求出∠GDE=∠GDA+∠ADE=∠ADC=90°即可;
(2)分别以G、E为圆心,以DG为半径画弧,两弧交于F,连接GF、EF即可;
(3)推出EF=CK,EF∥CK,根据平行四边形的判定推出即可.
【解答】(1)①证明:∵四边形ABCD是正方形,
∴AD=DC,∠GAD=∠DCE=90°,
在△GAD和△ECD中
∴△GAD≌△ECD(SAS),
∴DE=DG;
②∵四边形ABCD是正方形,
∴∠ADC=90°,
∵△GAD≌△ECD,
∴∠GDA=∠CDE,
∴∠GDE=∠GDA+∠ADE=∠CDE+∠ADE=∠ADC=90°,
∴DE⊥DG.
(2)解:如图所示:;
(3)四边形CEFK是平行四边形,
证明:∵四边形ABCD是正方形,
∴∠B=∠ECD=90°,BC=CD,
在△KBC和△ECD中
∴△KBC≌△ECD(SAS),
∴DE=CK,∠DEC=∠BKC,
∵∠B=90°,
∴∠KCB+∠BKC=90°,
∴∠KCB+∠DEC=90°,
∴∠EOC=180°﹣90°=90°,
∵四边形DGFE是正方形,
∴DE=EF=CK,∠FED=90°=∠EOC,
∴CK∥EF,
∴四边形CEFK是平行四边形.
【点评】本题考查了全等三角形的性质和判定,平行线的性质和判定,正方形性质的应用,主要考查学生的推理能力.
试题4、(2015春天水期末)如图所示:在△ABC中,分别以AB、AC、BC为边,在BC的同侧作等边△ABD、等边△ACE、等边△BCF.
(1)求证:四边形DAEF是平行四边形;
(2)探究下列问题:(只填条件,不需证明)
①当∠BAC满足 ∠BAC=150° 条件时,四边形DAEF是矩形;
②当∠BAC满足 ∠BAC=60° 条件时,以D、A、E、F为顶点的四边形不存在;
③当△ABC满足 ∠BAC=150°且AB=AC 条件时,四边形DAEF是正方形.
【分析】(1)由等边三角形的性质得出AC=CE=AE,AB=AD=BD,BC=CF=BF,∠BCF=∠ACE=60°,求出∠BCA=∠FCE,证△BCA≌△FCE,得出EF=BA=AD,同理DF=AC=AE,即可得出结论;
(2)①求出∠DAE的度数,根据矩形的判定得出即可;
②证出D、A、E三点共线,即可得出结论;
③由①得出四边形DAEF是矩形;再由AB=AC≠BC得出四边形DAEF是菱形,即可得出结论.
【解答】(1)证明:∵△ABD、△BCE、△ACE是等边三角形,
∴AC=CE=AE,AB=AD=BD,BC=CF=BF,∠BCF=∠ACE=60°,
∴∠BCA=∠FCE=60°﹣∠ACF,
在△BCA和△FCE中,
,
∴△BCA≌△FCE(SAS),
∴EF=BA=AD,
同理:DF=AC=AE,
∴四边形DAEF是平行四边形;
(2)解:①当∠A=150°时,四边形DAEF是矩形,理由如下:
∵△ABD、△ACE是等边三角形,
∴∠DAB=∠EAC=60°,
∴∠DAE=360°﹣60°﹣60°﹣150°=90°,
∵四边形DAEF是平行四边形,
∴四边形DAEF是矩形,
故答案为:=150°;
②当∠BAC=60°时,以D、A、E、F为顶点的四边形不存在;理由如下:
∵∠BAC=60°,∠BAD=∠CAE=60°,
∴点D、A、E共线,
∴以D、A、E、F为顶点的四边形不存在;
故答案为:∠BAC=60°;
③当△ABC满足∠BAC=150°,且AB=AC≠BC时,四边形DAEF是正方形,理由如下:
由①得:当∠BAC=150°时,四边形DAEF是矩形;
当AB=AC时,由(1)得:EF=AB=AD,DF=AC=AE,
∵AB=AC,
∴AD=AE,
∵四边形DAEF是平行四边形,
∴四边形DAEF是菱形,
∴四边形DAEF是正方形.
故答案为:∠BAC=150°,AB=AC.
【点评】本题考查了等边三角形的性质、全等三角形的性质和判定、平行四边形的判定、菱形的判定、矩形的判定以及正方形的判定;解此题的关键是求出EF=BA=AD,DF=AC=AE,主要考查了学生的推理能力.
试题5、(2011嘉兴)以四边形ABCD的边AB、BC、CD、DA为斜边分别向外侧作等腰直角三角形,直角顶点分别为E、F、G、H,顺次连接这四个点,得四边形EFGH.
(1)如图1,当四边形ABCD为正方形时,我们发现四边形EFGH是正方形;如图2,当四边形ABCD为矩形时,请判断:四边形EFGH的形状(不要求证明);
(2)如图3,当四边形ABCD为一般平行四边形时,设∠ADC=α(0°<α<90°),
①试用含α的代数式表示∠HAE;
②求证:HE=HG;
③四边形EFGH是什么四边形?并说明理由.
【分析】(1)根据等腰直角三角形的性质得到∠E=∠F=∠G=∠H=90°,求出四边形是矩形,根据勾股定理求出AH=HD=AD,DG=GC=CD,CF=BF=BC,AE=BE=AB,推出EF=FG=GH=EH,根据正方形的判定推出四边形EFGH是正方形即可;
(2)①根据平行四边形的性质得出,∠BAD=180°﹣α,根据△HAD和△EAB是等腰直角三角形,得到∠HAD=∠EAB=45°,求出∠HAE即可;
②根据△AEB和△DGC是等腰直角三角形,得出AE=AB,DG=CD,平行四边形的性质得出AB=CD,求出∠HDG=90°+a=∠HAE,根据SAS证△HAE≌△HDG,根据全等三角形的性质即可得出HE=HG;
③与②证明过程类似求出GH=GF,FG=FE,推出GH=GF=EF=HE,得出菱形EFGH,证△HAE≌△HDG,求出∠AHD=90°,∠EHG=90°,即可推出结论.
【解答】(1)解:四边形EFGH的形状是正方形.
(2)解:①∠HAE=90°+α,
在平行四边形ABCD中AB∥CD,
∴∠BAD=180°﹣∠ADC=180°﹣α,
∵△HAD和△EAB是等腰直角三角形,
∴∠HAD=∠EAB=45°,
∴∠HAE=360°﹣∠HAD﹣∠EAB﹣∠BAD=360°﹣45°﹣45°﹣(180°﹣a)=90°+α,
答:用含α的代数式表示∠HAE是90°+α.
②证明:∵△AEB和△DGC是等腰直角三角形,
∴AE=AB,DG=CD,
在平行四边形ABCD中,AB=CD,
∴AE=DG,
∵△AHD和△DGC是等腰直角三角形,
∴∠HDA=∠CDG=45°,
∴∠HDG=∠HDA+∠ADC+∠CDG=90°+α=∠HAE,
∵△AHD是等腰直角三角形,
∴HA=HD,
∴△HAE≌△HDG,
∴HE=HG.
③答:四边形EFGH是正方形,
理由是:由②同理可得:GH=GF,FG=FE,
∵HE=HG,
∴GH=GF=EF=HE,
∴四边形EFGH是菱形,
∵△HAE≌△HDG,
∴∠DHG=∠AHE,
∵∠AHD=∠AHG+∠DHG=90°,
∴∠EHG=∠AHG+∠AHE=90°,
∴四边形EFGH是正方形.
【点评】本题主要考查对正方形的判定,等腰直角三角形的性质,菱形的判定和性质,全等三角形的性质和判定,平行线的性质等知识点的理解和掌握,综合运用性质进行推理是解此题的关键.
正方形与矩形综合
试题1、(2013海安县校级模拟)正方形ABCD,矩形EFGH均位于第一象限内,它们的边平行于x轴或y轴,其中,点A,E在直线OM上,点C,G在直线ON上,O为坐标原点,点A的坐标为(3,3),正方形ABCD的边长为1.若矩形EFGH的周长为10,面积为6,则点F的坐标为 (7,5),(8,5) .
【分析】由A的坐标为(3,3),正方形ABCD的边长为1得出直线OM的解析式,再求出C点的坐标利用待定系数法求出直线ON的解析式;设矩形EFGH的宽为a,则长为5﹣a,再根据面积为6即可得出a的值,由点E在直线OM上设点E的坐标为(e,e),由矩形的边长可用e表示出F、G点的坐标,再根据G点在直线ON上得出e的值,即可得出结论.
【解答】解:∵A的坐标为(3,3),
∴直线OM的解析式为y=x,
∵正方形ABCD的边长为1,
∴C(4,2),
设直线ON的解析式为y=kx(k≠0),
∴2=4k,
解得k=,
∴直线ON的解析式为:y=x;
设矩形EFGH的宽为a,则长为5﹣a,
∵矩形EFGH的面积为6,
∴a(5﹣a)=6,
解得:a=2或a=3,
当a=2即EF=2时,EH=5﹣2=3,
∵点E在直线OM上,设点E的坐标为(e,e),
∴F(e,e﹣2),G(e+3,e﹣2),
∵点G在直线ON上,
∴e﹣2=(e+3),
解得:e=7,
∴F(7,5);
当a=3即EF=3时,EH=5﹣3=2,
∵点E在直线OM上,设点E的坐标为(e,e),
∴F(e,e﹣3),G(e+2,e﹣3),
∵点G在直线ON上,
∴e﹣3=(e+2),
解得:e=8,
∴F(8,5).
故答案为:(7,5),(8,5).
【点评】本题考查了正方形的性质、矩形的性质、一次函数解析式的求法;根据题意得出直线ON的解析式是解答此题的关键,在解答时要注意进行分类讨论.
试题2、(2016春江阴市月考)如图,在正方形ABCD中,点P在AD上,且不与A、D重合,BP的垂直平分线分别交CD、AB于E、F两点,垂足为Q,过E作EH⊥AB于H.
(1)求证:HF=AP;
(2)若正方形ABCD的边长为12,AP=4,求线段AF的长.
【分析】(1)由正方形的性质和已知条件可分别证明∠FEH=∠PBA,AB=HE,进而可证明△ABP≌△HEF,由全等三角形的性质即可得到HF=AP;
(2)连接,设AF=x,则PF=BF=12﹣x,在△APF中利用勾股定理可得:42+x2=(12﹣x)2,解方程求出x的值即可.
【解答】解:(1)∵EF⊥BP,EH⊥AB,
∴∠FEH+∠EMQ=90°=∠PBA+∠BMH,
又∵∠QME=∠BMH,
∴∠FEH=∠PBA,
∵四边形ABCD是正方形,
∴∠A=∠D=90°,AB=AD,
∵EH⊥AB,
∴∠EHA=90°=∠A=∠D,
∴四边形ADEH是矩形,
∴AD=EH,
又∵AB=AD,
∴AB=EH,
在△ABP与△HEF中
,
∴△ABP≌△HEF(ASA),
∴AP=FH;
(2)连结PF,
∵EF垂直平分BP,
∴PF=BF,
设AF=x,则PF=BF=12﹣x,
∴在△APF中,42+x2=(12﹣x)2,
∴x=,
∴AF=.
【点评】本题考查的是正方形的性质、勾股定理的运用、全等三角形的判定和性质以及线段垂直平分线的性质,熟知正方形的性质及全等三角形的判定与性质是解答此题的关键.
试题3、(2015春霸州市期末)如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.
(1)试说明EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形并证明你的结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论.
【分析】(1)根据CE平分∠ACB,MN∥BC,找到相等的角,即∠OEC=∠ECB,再根据等边对等角得OE=OC,同理OC=OF,可得EO=FO.
(2)利用矩形的判定解答,即有一个内角是直角的平行四边形是矩形.
(3)利用已知条件及正方形的性质解答.
【解答】解:(1)∵CE平分∠ACB,
∴∠ACE=∠BCE,
∵MN∥BC,
∴∠OEC=∠ECB,
∴∠OEC=∠OCE,
∴OE=OC,
同理,OC=OF,
∴OE=OF.
(2)当点O运动到AC中点处时,四边形AECF是矩形.
如图AO=CO,EO=FO,
∴四边形AECF为平行四边形,
∵CE平分∠ACB,
∴∠ACE=∠ACB,
同理,∠ACF=∠ACG,
∴∠ECF=∠ACE+∠ACF=(∠ACB+∠ACG)=×180°=90°,
∴四边形AECF是矩形.
(3)△ABC是直角三角形
∵四边形AECF是正方形,
∴AC⊥EN,故∠AOM=90°,
∵MN∥BC,
∴∠BCA=∠AOM,
∴∠BCA=90°,
∴△ABC是直角三角形.
【点评】本题主要考查利用平行线的性质“等角对等边”证明出结论(1),再利用结论(1)和矩形的判定证明结论(2),再对(3)进行判断.解答时不仅要注意用到前一问题的结论,更要注意前一问题为下一问题提供思路,有相似的思考方法.是矩形的判定和正方形的性质等的综合运用.
试题4、(2015春万州区期末)如图,在正方形ABCD中,点E、F、G、H分别在四边上,EH∥BC,GF∥AB,EH与FG交于点O,且AE=AG,若AE比CH长2,△BOF的面积为
(1)求正方形ABCD的面积;
(2)设AE=a,BE=b,求代数式a4+b4的值.
【分析】(1)根据四边形ABCD是正方形,得到AD∥BC,AD=BC,AB∥CD,AB=CD,由于EH∥BC,GF∥AB,得出四边形AEOG是正方形,四边形AEHD,EBFO,GOHD是矩形,根据△BOF的面积为,得到矩形EBFO的面积=3,设AE=OE=DH=x,BE=CH=y,列出,即可得到结果;
(2)由(1)求得AE=3,BE=1,代入即可得到结果.
【解答】解:(1)∵四边形ABCD是正方形,
∴AD∥BC,AD=BC,AB∥CD,AB=CD,
∵EH∥BC,GF∥AB,
∴四边形AEOG是正方形,四边形AEHD,EBFO,GOHD是矩形,
∴AE=DH,BE=CH,
∵△BOF的面积为,
∴矩形EBFO的面积=3,
设AE=OE=DH=x,BE=CH=y,
∴,
∴,
∴AEE=3,BE=1,
∴AB=AE+BE=4,
∴正方形ABCD的面积=4×4=16;
(2)由(1)求得AE=3,BE=1,
∴a=3,b=1,
∴a4+b4=34+11=82.
【点评】本题考查了正方形的判定和性质,正方形的面积,三角形的面积,充分利用已知条件列方程组求出各线段是解题的关键.
试题5、(2015春冷水江市校级期末)如图,矩形ABCD和正方形ECGF.其中E、H分别为AD、BC中点.连结AF、HG、AH.
(1)求证:AF=HG;
(2)求证:∠FAD=∠GHC;
(3)试探究∠FAH与∠AFE的关系.
【分析】(1)根据矩形的性质和已知得出AE=HC,AE∥HC,求出四边形AHCE为平行四边形,根据平行四边形的性质得出AH=EC,AH∥EC,求出四边形AHGF是平行四边形,即可得出答案;
(2)根据平行线得出∠FAH+∠AHG=180°,求出∠DAH=∠AHB,根据∠AHB+∠AHG+∠GHC=180°即可得出答案;
(3)过A点作AM∥EF,根据平行线的性质得出∠MAF=∠AFE,求出MA⊥AH,根据垂直得出∠MAF+∠FAH=90°,即可得出答案.
【解答】(1)证明:∵四边形ABCD是矩形,且E、H分别为AD、BC的中点,
∴AE=HC,AE∥HC,
∴四边形AHCE为平行四边形,
∴AH=EC,AH∥EC,
又∵四边形ECGF为正方形,
∴EC=FG,EC∥FG,
∴AH=FG,AH∥FG,
∴四边形AHGF是平行四边形,
∴AH=FG;
(2)证明:∵四边形AHGF是平行四边形,
∴∠FAH+∠AHG=180°,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DAH=∠AHB,
又∵∠AHB+∠AHG+∠GHC=180°,
∴∠FAD=∠GHC;
(3)∠FAH+∠AFE=90°,
证明:过A点作AM∥EF,
则∠MAF=∠AFE,
∵AM∥EF,AH∥EC,FE⊥EC,
∴MA⊥AH,
∴∠MAF+∠FAH=90°,
∴∠FAH+∠MAF=90°.
【点评】本题考查了矩形的性质,平行四边形的性质和判定,正方形的性质的应用,能综合运用知识点进行推理是解此题的关键.
正方形与菱形综合
试题1、(2012深圳模拟)如图,正方形ABCD的边长为2,以对角线BD为边作菱形BEFD,点C、E、F在同一直线上.
(1)求∠EBC的度数;
(2)求CE的长.
【分析】(1)首先连接AC交BD于点O,过点E作EH⊥BD于点H,由正方形ABCD的边长为2,四边形BEFD是菱形,易求得BE=BD=2,由BD∥EF,可求得EH=OC=,然后由三角函数的性质,求得∠EBC的度数;
(2)首先过点E作EG⊥BC,交BC的延长线于点G,即可得△ECG是等腰直角三角形,然后设EG=CG=x,在Rt△BEG中,由BE2=BG2+EG2,可得方程:(2)2=(2+x)2+x2,解此方程即可求得EG的长,继而求得CE的长.
【解答】解:(1)连接AC交BD于点O,过点E作EH⊥BD于点H,
∵正方形ABCD的边长为2,
∴BD=AC=2,AC⊥BD,
∴OC=AC=,
∵四边形BEFD是菱形,
∴BE=BD=2,BD∥EF,
∵点C、E、F在同一直线上,
∴EH=OC=,
在Rt△BEH中,sin∠EBH===,
∴∠EBH=30°,
∴∠EBC=∠DBC﹣∠EBH=45°﹣30°=15°;
(2)过点E作EG⊥BC,交BC的延长线于点G,
∵BD∥EF,
∴∠ECG=∠DBC=45°,
∴△ECG是等腰直角三角形,
∴EG=CG,
设EG=x,
则BG=BC+CG=2+x,
在Rt△BEG中,BE2=BG2+EG2,
即(2)2=(2+x)2+x2,
即2x2+4x﹣4=0,
解得:x=﹣1或x=﹣﹣1(舍去),
∴EG=﹣1,
∴CE=EG=(﹣1)=﹣.
【点评】此题考查了正方形的性质、菱形的性质、特殊角的三角函数值以及勾股定理的知识.此题难度较大,注意掌握辅助线的作法,注意数形结合与方程思想的应用.
试题2、(2013春莒南县期末)如图,正方形ABCD的边长为2,以对角线AC为一边作菱形AEFC,AF于BC交于G点,则∠BCE的度数与BE的长分别为( )
A.30°、
B.30°、
C.22.5°、
D.22.5°、
【分析】根据正方形的对角线平分一组对角可得∠BAC=∠ACB=45°,根据菱形的四条边都相等可得AC=AE,然后根据等腰三角形两底角相等求出∠ACE,然后根据∠BCE=∠ACE﹣∠ACB计算即可得解;再根据正方形的对角线等于边长的倍求出AE=AC,然后根据BE=AE﹣AB计算即可得解.
【解答】解:在正方形ABCD中,∠BAC=∠ACB=45°,
∵四边形AEFC是菱形,
∴AC=AE,
∴∠ACE=(180°﹣∠BAC)=(180°﹣45°)=67.5°,
∴∠BCE=∠ACE﹣∠ACB=67.5°﹣45°=22.5°,
∵正方形ABCD的边长为2,
∴AE=AC=2,
∴BE=AE﹣AB=2﹣2.
故选C.
【点评】本题考查了正方形的性质,菱形的性质,等边对等角的性质,熟记两图形的性质并准确识图是解题的关键.
试题3、(2015春遂宁期末)如图,正方形ABCD的对角线AC是菱形AEFC的一边,则∠FAB的度数为 22.5° .
【分析】根据正方形的性质求出∠BAC=45°,再根据菱形的对角线平分一组对角解答即可.
【解答】解:∵四边形ABCD是正方形,
∴∠BAC=45°,
∵四边形AEFC是菱形,
∴∠FAB=∠BAC=×45°=22.5°.
故答案为:22.5°.
【点评】本题考查了正方形的对角线平分一组对角,菱形的对角线平分一组对角的性质,熟记性质是解题的关键.
试题4、(2014重庆校级二模)如图,已知正方形ABCD的边长为3,菱形EFGH的三个顶点E、G、H分别落在正方形的边AB、CD、DA上,AH=1,则GC长度的取值范围是 3﹣≤GC≤3 .
【分析】由菱形边长来确定GC长度的取值范围.
【解答】解:∵AH=1,
∴HE的最大值为==,
此时DG==,
∴此时GC=3﹣,
当G与点D重合时,菱形的边最小,
∴3﹣≤GC≤3.
故答案为:3﹣≤GC≤3.
【点评】本题主要考查了正方形的性质及菱形的性质,解题的关键是由菱形边长来确定GC长度的取值范围.
试题5、(2014春椒江区校级期中)如图,ABCD是正方形,E是CF上一点,若DBEF是菱形,则∠EBC= 15° .
【分析】过D作DG垂直于CF,垂足为G,由正方形的性质可得出正方形的四条边相等,且四个角为直角,三角形BCD为等腰直角三角形,可得出∠BDC与∠DBC都为45°,设正方形的边长为1,根据勾股定理求出BD的长为,即菱形的四条边为,由DG与FC垂直,且BD与EF平行,可得BD垂直于DG,进而得到∠CDG为45°,即三角形DCG为等腰直角三角形,由DC的长为1,可求出DG为,在直角三角形DFG中,由DG为DF的一半,得到∠F为30°,再根据菱形的对角相等,可得∠DBE为30°,由∠EBC=∠DBC﹣∠DBE求出度数即可.
【解答】解:过D作DG⊥CF,垂足为G,如图所示:
∵四边形ABCD为正方形,
∴∠CBD=∠CDB=45°,∠BCD=90°,
设正方形ABCD的边长为1,即AB=BC=CD=AD=1,
∴根据勾股定理得:BD==,
∵四边形BEFD为菱形,
∴BE=EF=DF=BD=,
又∵BD∥EF,DG⊥FC,
∴BD⊥DG,即∠BDG=90°,
∴∠CDG=∠BDG﹣∠BDC=90°﹣45°=45°,又∠DGC=90°,
∴△DCG为等腰直角三角形,又DC=1,
∴DG=DCsin45°=,又DF=,
在Rt△DFG中,由DG=DF,
∴∠F=30°,
∴∠DBE=30°,
则∠EBC=∠DBC﹣∠DBE=45°﹣30°=15°.
故答案是:15°.
【点评】此题考查了正方形的性质,菱形的性质,等腰直角三角形的性质以及直角三角形的性质,根据题意作出辅助线DG是本题的突破点,熟练掌握图形的性质是解本题的关键.
试题6、(2015荆州)如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
【分析】(1)先证出△ABP≌△CBP,得PA=PC,由于PA=PE,得PC=PE;
(2)由△ABP≌△CBP,得∠BAP=∠BCP,进而得∠DAP=∠DCP,由PA=PC,得到∠DAP=∠E,∠DCP=∠E,最后∠CPF=∠EDF=90°得到结论;
(3)借助(1)和(2)的证明方法容易证明结论.
【解答】(1)证明:在正方形ABCD中,AB=BC,
∠ABP=∠CBP=45°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE;
(2)由(1)知,△ABP≌△CBP,
∴∠BAP=∠BCP,
∴∠DAP=∠DCP,
∵PA=PE,
∴∠DAP=∠E,
∴∠DCP=∠E,
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠E,
即∠CPF=∠EDF=90°;
(3)在菱形ABCD中,AB=BC,∠ABP=∠CBP=60°,
在△ABP和△CBP中,
,
∴△ABP≌△CBP(SAS),
∴PA=PC,∠BAP=∠BCP,
∵PA=PE,
∴PC=PE,
∴∠DAP=∠DCP,
∵PA=PC,
∴∠DAP=∠AEP,
∴∠DCP=∠AEP
∵∠CFP=∠EFD(对顶角相等),
∴180°﹣∠PFC﹣∠PCF=180°﹣∠DFE﹣∠AEP,
即∠CPF=∠EDF=180°﹣∠ADC=180°﹣120°=60°,
∴△EPC是等边三角形,
∴PC=CE,
∴AP=CE.
【点评】本题考查了正方形的性质,全等三角形的判定与性质,菱形的性质,等边对等角的性质,熟记正方形的性质确定出∠ABP=∠CBP是解题的关键.
正方形与正方形综合
试题1、(2016贵阳模拟)将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
A.2cm2
B.4cm2
C.6cm2
D.8cm2
【分析】连接AP、AN,点A是正方形的对角线的交点,则AP=AN,∠APF=∠ANE=45°,易得PAF≌△NAE,进而可得四边形AENF的面积等于△NAP的面积,同理可得答案.
【解答】解:如图,连接AP,AN,点A是正方形的对角线的交
则AP=AN,∠APF=∠ANE=45°,
∵∠PAF+∠FAN=∠FAN+∠NAE=90°,
∴∠PAF=∠NAE,
∴△PAF≌△NAE,
∴四边形AENF的面积等于△NAP的面积,
而△NAP的面积是正方形的面积的,而正方形的面积为4,
∴四边形AENF的面积为1cm2,四块阴影面积的和为4cm2.
故选B.
【点评】本题考查旋转的性质.旋转变化前后,对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所构成的旋转角相等.要注意旋转的三要素:①定点﹣旋转中心;②旋转方向;③旋转角度.
试题2、现有一张边长等于a(a>16)的正方形纸片,从距离正方形的四个顶点8cm处,沿45°角画线,将正方形纸片分成5部分,则阴影部分是 正方形 (填写图形的形状)(如图),它的一边长是 cm .
【分析】延长小正方形的一边交大正方形于一点,连接此点与距大正方形顶点8cm处的点,构造直角边长为8的等腰直角三角形,将小正方形的边长转化为等腰直角三角形的斜边长来求解即可.
【解答】解:如图,作AB平行于小正方形的一边,延长小正方形的另一边与大正方形的一边交于B点,
∴△ABC为直角边长为8cm的等腰直角三角形,
∴AB=AC=8,
∴阴影正方形的边长=AB=8
cm.
故答案为:正方形,
cm.
【点评】本题考查了正方形的性质与勾股定理的知识,题目同时也渗透了转化思想
试题3、已知,正方形CEFG的边GC在正方形ABCD的边CD上,延长CD到H,使DH=CE,K在BC边上,且BK=CE,求证:四边形AKFH为正方形.
【分析】根据正方形的性质得出AB=BC=CD=AD,∠BAD=∠DCB=∠B=∠ADC=90°,∠GCE=∠E=∠GFE=∠CGF=90°,求出∠ADH=∠HGF=∠E=∠B=90°,BK=GF=DH=EF,KE=GH=AB=AD,证△ABK≌△KEF≌△HGF≌△ADH,根据全等三角形的性质推出AK=KF=HF=AH,∠BAK=HAD,求出∠HAK=∠BAD=90°,根据正方形的判定得出即可.
【解答】证明:∵四边形ABCD和四边形CEFG是正方形,
∴AB=BC=CD=AD,∠BAD=∠DCB=∠B=∠ADC=90°,∠GCE=∠E=∠GFE=∠CGF=90°,
∴∠ADH=∠HGF=∠E=∠B=90°,
∵DH=CE,BK=CE,
∴BK=GF=DH=EF,KE=GH=AB=AD,
在△ABK、△KEF、△HGF、△ADH中
∴△ABK≌△KEF≌△HGF≌△ADH,
∴AK=KF=HF=AH,∠BAK=HAD,
∵∠BAD=90°,
∴∠HAK=∠HAD+∠DAK=∠BAK+∠DAK=∠BAD=90°,
∴四边形AKFH为正方形.
【点评】本题考查了正方形的性质和判定,全等三角形的性质和判定的应用,解此题的关键是推出△ABK≌△KEF≌△HGF≌△ADH,注意:有一个角是直角的菱形是正方形.
试题5、(2013历城区一模)如图,四边形ABCD、DEFG都是正方形,连接AE、CG,AE与CG相交于点M.下列结论:①AE=CG,②AE⊥CG,③DM∥GE,④OM=OD,⑤∠DME=45°.正确结论的个数为( )
A.2个
B.3个
C.4个
D.5个
【分析】根据正方形的性质可得AD=CD,DE=DG,∠ADC=∠EDG=90°,然后求出∠ADE=∠CDG,再利用“边角边”证明△ADE和△CDF全等,根据全等三角形对应边相等可得AE=CG,判定①正确;根据全等三角形对应角相等可得∠1=∠2,再求出∠MEG+∠MGE=∠DEG+∠DGE=90°,然后求出∠EMG=90°,判定②正确;根据直角三角形斜边上的中线等于斜边的一半可得OM=OD=GE,判定④正确;求出点D、E、G、M四点共圆,再根据同弧所对的圆周角相等可得∠DME=∠DGE=45°,判定⑤正确;根据∠MGE≠45°可得∠DME≠∠MGE,判定DM∥GE错误.
【解答】解:∵四边形ABCD、DEFG都是正方形,
∴AD=CD,DE=DG,∠ADC=∠EDG=90°,
∴∠ADC+∠ADG=∠EDG+∠ADG,
即∠ADE=∠CDG,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(SAS),
∴AE=CG,故①正确;
∠1=∠2,
∵∠MEG+∠MGE=∠MEG+∠DGE+∠1=∠MEG+∠2+∠DGE=∠DEG+∠DGE=45°+45°=90°,
∴∠EMG=180°﹣(∠MEG+∠MGE)=180°﹣90°=90°,
∴AE⊥CG,故②正确;
∵O是正方形DEFG的对角线的交点,
∴OE=OG,
∴OM=OD=GE,故④正确;
∵∠EMG=∠EDG=90°,
∴点D、E、G、M四点共圆,
∴∠DME=∠DGE=45°,故⑤正确;
⑤方法二:过D作DP⊥EM于P,DQ⊥CG于Q,
在△GQD与△EPD中,,
∴△GQD≌△EPD,
∴DQ=DP,
∴MD是∠CME的平分线,
∴∠DME=∠CME=45°,故⑤正确;
∵∠MGE≠∠DEG=45°,
∴∠DME≠∠MGE,
∴DM∥GE不成立,故③错误;
综上所述,正确的有①②④⑤共4个.
故选C.
【点评】本题考查了正方形的性质,全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,以及四点共圆,熟练掌握各性质是解题的关键.
试题6、(2014万州区校级模拟)如图,正方形ABCD绕B点逆时针旋转得到正方形BPQR,连接DQ,延长CP交DQ于E.若CE=5,ED=4,则AB= .
【分析】设AD与PQ相交于点O,连接BO,过点C作CM⊥DQ角QD的延长线于M,利用“HL”证明Rt△AOB和Rt△POB全等,根据全等三角形对应边相等可得∠ABO=∠PBO,全等三角形对应边相等可得AO=PO,然后求出OD=OQ,根据等边对等角可得∠ODQ=∠OQD,再根据三角形的内角和定理和四边形的内角和定理求出∠PBO=∠ODQ,再根据等腰三角形两底角相等的性质用∠POB表示出∠PCB,然后求出∠EDB=∠PCB,根据三角形的内角和定理可得∠CED=∠CBD=45°,判断出△CEM是等腰直角三角形,根据等腰直角三角形的性质求出CM=EM=5,再求出DM,然后利用勾股定理列式计算即可求出CD的长,根据正方形的四条边都相等即可得解.
【解答】解:如图,设AD与PQ相交于点O,连接BO,过点C作CM⊥DQ角QD的延长线于M,
在Rt△AOB和Rt△POB中,
,
∴Rt△AOB≌Rt△POB(HL),
∴∠ABO=∠PBO,AO=PO,
∴AD﹣AO=PQ﹣PO,
即OD=OQ,
∴∠ODQ=∠OQD,
∵∠PBO=(360°﹣90°×2﹣∠AOP)=(180°﹣∠AOP),
∠ODQ=(180°﹣∠DOQ),
∠AOP=∠DOQ(对顶角相等),
∴∠PBO=∠ODQ,
∵BC=BP,
∴∠PCB=(180°﹣∠PBC)=(180°﹣90°+2∠POB)=45°+∠PBO,
∠EDB=∠ODQ+∠ADB=∠PBO+45°,
∴∠EDB=∠PCB,
∴∠CED=∠CBD=45°,
∴△CEM是等腰直角三角形,
∵CE=5,
∴CM=EM=5,
∴DM=EM﹣ED=5﹣4=1,
在Rt△CDM中,CD===,
∴AB=CD=.
故答案为:.
【点评】本题考查了正方形的性质,全等三角形的判定与性质,三角形的内角和定理,
