人教版三年级数学下册第八单元数学广角——搭配单元检测(含答案)
文档属性
| 名称 | 人教版三年级数学下册第八单元数学广角——搭配单元检测(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-25 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版三年级数学下册第八单元搭配单元检测
一、单选题(10分)
1.运动会上,三(1)班将派出4位同学参加4×100米接力赛,小江跑得最快老师将他安排在最后一棒。这四名同学跑接力赛一共有( )种排法。
A.12 B.8 C.6
2.用 可以组成 ( ) 个没有重复数字的两位数。
A.7 B.9 C.12 D.15
3.书架上有4本不同的科技书和5本不同的故事书,天天想借一本科技书和一本故事书,有( )种不同的借法。
A.20 B.16 C.9 D.25
4.奶茶店有3种奶茶和2道小吃,小华想点一杯奶茶和一道小吃,有( )种搭配方法。
A.2 B.3 C.5 D.6
5.学校体育室里有篮球、排球、羽毛球、足球四种球,体育课代表到体育室借两种球,有( )种不同的借法。
A.4 B.5 C.6
二、判断题(10分)
6.用0、2、3、4可以组成12个没有重复数字的两位数。( )
7.有五个排球队,每两队之间比赛一场,一共要比赛20场。( )
8.用0、4、7、8可以组成8个不同的两位数。( )
9.如图,从学校到图书馆共有6条路可以走。( )
10.有3双袜子,2双鞋子,一共有5种不同的穿法。( )
三、填空题(28分)
11.垃圾分类环保先行。垃圾可分为:有害垃圾、可回收垃圾、厨余垃圾、其他垃圾。四种分类垃圾桶提成一排(如图),一共有 种不同的摆法。如果“其他垃圾”桶不能摆在最左边,那么一共有 种不同的摆法。
12.小红,小亮,小米,三个好朋友每两人互相送一件小礼物,他们一共送了 次礼物:在“六一”儿童节这天他们又每两人互通一次电话,一共通话 次。
13.用2、0、7、6可以组成 个没有重复数字的两位数,其中组成的最小两位数是 。
14.兔妹到猴哥家作客,它一共有 条路可以选择。
15.4个分类垃圾桶摆成一排,如果“有害垃圾”桶的位置摆在最左边不动,其他3个垃圾桶可以任意换位置,这样的摆法一共有 种。
16.甲、乙、丙三人排成一排拍照,如果丙排在中间,一共有 种不同的排法。
17.有4个同学聚会,每两个人握一次手,全都握一遍,一共要握 次手。
18.从一枚1元硬币、一枚5角硬币和两枚1角硬币中任意取两枚,可以组成 种不同的币值。
19.蚂蚁之间有一种特殊的交流方式,它们通过触碰触角交流信息。有5只蚂蚁,每2只碰一次触角,它们一共需要碰 次触角。
20.小红和4个好朋友,每两人通一次电话,她们一共要通 次电话。
21.小东、小明、小芳三个人进行乒乓球单打比赛,每两个人之间都要比赛一场,一共要比 场。
四、操作题(4分)
22.用红、黄、蓝三种颜料在同一个圆环(如图)的三个部分中分别涂上不同的颜色,有多少种不同的涂法?请你涂一涂。
五、连线题(6分)
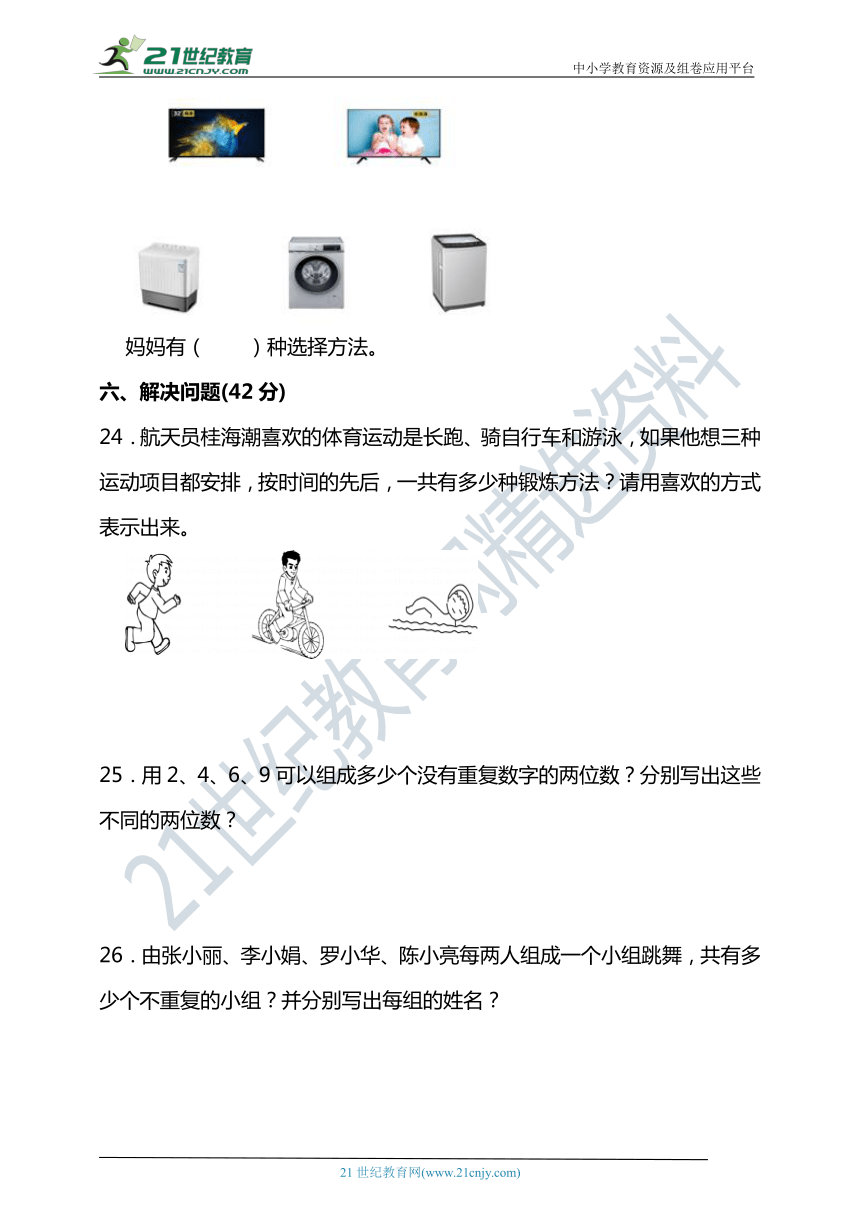
23.京东商城有促销活动,妈妈想买一台电视机和一台洗衣机,请用连线表示她可以怎样选择。
妈妈有( )种选择方法。
六、解决问题(42分)
24.航天员桂海潮喜欢的体育运动是长跑、骑自行车和游泳,如果他想三种运动项目都安排,按时间的先后,一共有多少种锻炼方法?请用喜欢的方式表示出来。
25.用2、4、6、9可以组成多少个没有重复数字的两位数?分别写出这些不同的两位数?
26.由张小丽、李小娟、罗小华、陈小亮每两人组成一个小组跳舞,共有多少个不重复的小组?并分别写出每组的姓名?
27.一个三位小数,整数部分小于3,十分位上不是0~7,百分位上不是0~6,千分位上是7~9,这个三位小数一共有多少种可能?
28.小华、小明、小东、小勇四个好朋友一起到公园去游玩,四个人站成一排拍一张照片,如果小华站在最右边,有多少种不同的站队方法?每两人租一条小船,有几种不同的搭配方法?
29.李叔叔来到了新房,新房有4个房间,也有4把钥匙,他知道每把钥匙只能开一个房门,但不知道哪把钥匙开哪一个房门,现在要打开所有关闭的4个房门,那么他至少要试开多少次才能打开全部?
30.孙悟空在和妖怪斗法的时候,把自己的名字“孙行者”三个字变化了许多次,能变出多少个与原来不同的名字?
答案
1.C
2.B
3.A
4.D
5.C
6.×
7.×
8.×
9.×
10.×
11.24;18
12.6;3
13.9;20
14.4
15.6
16.2
17.6
18.4
19.10
20.10
21.3
22.解:
3×2=6(种)
答:有6种不同的涂法。
23.解:连线如下:
妈妈有6种选择方法。
24.解:3×2×1=6(种)
长跑、骑自行车、游泳,
长跑、游泳、骑自行车,
游泳、长跑、骑自行车,
游泳、骑自行车、长跑,
骑自行车、长跑、游泳,
骑自行车、游泳、长跑,
答:一共有6种锻炼方法。
25.解:24、26、29、46、49、69、42、62、92、64、94、96。
26.解:4×3÷2=6(个)
张小丽、李小娟; 张小丽、罗小华; 张小丽、陈小亮;
李小娟、罗小华; 李 小娟、陈小亮; 罗小华、陈小亮。
答:共有6个不重复的小组。
27.解:整数部分为0,1,2;十分位为8,9;百分位为7,8,9;千分位为7,8,9,故
共54种可能。
28.解:3+2+1=6(种)
答:有6种不同的站队方法,6种不同的搭配方法。
29.解:3+2+1=6(次)
答:至少试6次。
30.解:孙者行,者行孙,者孙行,行者孙,行孙者,共5个与原来不同的名字。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
人教版三年级数学下册第八单元搭配单元检测
一、单选题(10分)
1.运动会上,三(1)班将派出4位同学参加4×100米接力赛,小江跑得最快老师将他安排在最后一棒。这四名同学跑接力赛一共有( )种排法。
A.12 B.8 C.6
2.用 可以组成 ( ) 个没有重复数字的两位数。
A.7 B.9 C.12 D.15
3.书架上有4本不同的科技书和5本不同的故事书,天天想借一本科技书和一本故事书,有( )种不同的借法。
A.20 B.16 C.9 D.25
4.奶茶店有3种奶茶和2道小吃,小华想点一杯奶茶和一道小吃,有( )种搭配方法。
A.2 B.3 C.5 D.6
5.学校体育室里有篮球、排球、羽毛球、足球四种球,体育课代表到体育室借两种球,有( )种不同的借法。
A.4 B.5 C.6
二、判断题(10分)
6.用0、2、3、4可以组成12个没有重复数字的两位数。( )
7.有五个排球队,每两队之间比赛一场,一共要比赛20场。( )
8.用0、4、7、8可以组成8个不同的两位数。( )
9.如图,从学校到图书馆共有6条路可以走。( )
10.有3双袜子,2双鞋子,一共有5种不同的穿法。( )
三、填空题(28分)
11.垃圾分类环保先行。垃圾可分为:有害垃圾、可回收垃圾、厨余垃圾、其他垃圾。四种分类垃圾桶提成一排(如图),一共有 种不同的摆法。如果“其他垃圾”桶不能摆在最左边,那么一共有 种不同的摆法。
12.小红,小亮,小米,三个好朋友每两人互相送一件小礼物,他们一共送了 次礼物:在“六一”儿童节这天他们又每两人互通一次电话,一共通话 次。
13.用2、0、7、6可以组成 个没有重复数字的两位数,其中组成的最小两位数是 。
14.兔妹到猴哥家作客,它一共有 条路可以选择。
15.4个分类垃圾桶摆成一排,如果“有害垃圾”桶的位置摆在最左边不动,其他3个垃圾桶可以任意换位置,这样的摆法一共有 种。
16.甲、乙、丙三人排成一排拍照,如果丙排在中间,一共有 种不同的排法。
17.有4个同学聚会,每两个人握一次手,全都握一遍,一共要握 次手。
18.从一枚1元硬币、一枚5角硬币和两枚1角硬币中任意取两枚,可以组成 种不同的币值。
19.蚂蚁之间有一种特殊的交流方式,它们通过触碰触角交流信息。有5只蚂蚁,每2只碰一次触角,它们一共需要碰 次触角。
20.小红和4个好朋友,每两人通一次电话,她们一共要通 次电话。
21.小东、小明、小芳三个人进行乒乓球单打比赛,每两个人之间都要比赛一场,一共要比 场。
四、操作题(4分)
22.用红、黄、蓝三种颜料在同一个圆环(如图)的三个部分中分别涂上不同的颜色,有多少种不同的涂法?请你涂一涂。
五、连线题(6分)
23.京东商城有促销活动,妈妈想买一台电视机和一台洗衣机,请用连线表示她可以怎样选择。
妈妈有( )种选择方法。
六、解决问题(42分)
24.航天员桂海潮喜欢的体育运动是长跑、骑自行车和游泳,如果他想三种运动项目都安排,按时间的先后,一共有多少种锻炼方法?请用喜欢的方式表示出来。
25.用2、4、6、9可以组成多少个没有重复数字的两位数?分别写出这些不同的两位数?
26.由张小丽、李小娟、罗小华、陈小亮每两人组成一个小组跳舞,共有多少个不重复的小组?并分别写出每组的姓名?
27.一个三位小数,整数部分小于3,十分位上不是0~7,百分位上不是0~6,千分位上是7~9,这个三位小数一共有多少种可能?
28.小华、小明、小东、小勇四个好朋友一起到公园去游玩,四个人站成一排拍一张照片,如果小华站在最右边,有多少种不同的站队方法?每两人租一条小船,有几种不同的搭配方法?
29.李叔叔来到了新房,新房有4个房间,也有4把钥匙,他知道每把钥匙只能开一个房门,但不知道哪把钥匙开哪一个房门,现在要打开所有关闭的4个房门,那么他至少要试开多少次才能打开全部?
30.孙悟空在和妖怪斗法的时候,把自己的名字“孙行者”三个字变化了许多次,能变出多少个与原来不同的名字?
答案
1.C
2.B
3.A
4.D
5.C
6.×
7.×
8.×
9.×
10.×
11.24;18
12.6;3
13.9;20
14.4
15.6
16.2
17.6
18.4
19.10
20.10
21.3
22.解:
3×2=6(种)
答:有6种不同的涂法。
23.解:连线如下:
妈妈有6种选择方法。
24.解:3×2×1=6(种)
长跑、骑自行车、游泳,
长跑、游泳、骑自行车,
游泳、长跑、骑自行车,
游泳、骑自行车、长跑,
骑自行车、长跑、游泳,
骑自行车、游泳、长跑,
答:一共有6种锻炼方法。
25.解:24、26、29、46、49、69、42、62、92、64、94、96。
26.解:4×3÷2=6(个)
张小丽、李小娟; 张小丽、罗小华; 张小丽、陈小亮;
李小娟、罗小华; 李 小娟、陈小亮; 罗小华、陈小亮。
答:共有6个不重复的小组。
27.解:整数部分为0,1,2;十分位为8,9;百分位为7,8,9;千分位为7,8,9,故
共54种可能。
28.解:3+2+1=6(种)
答:有6种不同的站队方法,6种不同的搭配方法。
29.解:3+2+1=6(次)
答:至少试6次。
30.解:孙者行,者行孙,者孙行,行者孙,行孙者,共5个与原来不同的名字。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
