人教八下16.3.1 二次根式的加减第1课时 课件(共28张PPT)
文档属性
| 名称 | 人教八下16.3.1 二次根式的加减第1课时 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 08:57:59 | ||
图片预览








文档简介
(共28张PPT)
人教版数学八年级下册
第十六章 二次根式
汇报人:孙老师
汇报班级:X级X班
第1课时 二次根式的加减
16.3 二次根式的加减
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.掌握合并被开方数相同的最简二次根式的方法.
2.熟练运用二次根式的加、减运算法则进行计算.
第贰章节
新课导入
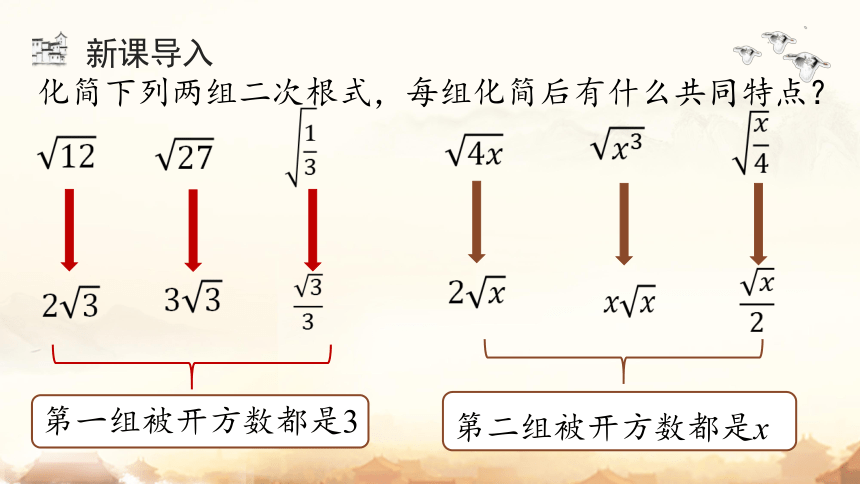
新课导入
化简下列两组二次根式,每组化简后有什么共同特点?
第二组被开方数都是x
第一组被开方数都是3
第叁章节
新知探究
新知探究
整式的加减
找同类项
合并同类项
二次根式的加减
合并同类二次根式
找同类
二次根式
类 比
知识点1:二次根式的加减
例如: 2 a + a =
(2 + 1) a = 3a
?
合作探究
观察下列二次根式有什么共同特征:
每组的二次根式的被开方数相同
下列二次根式又有什么共同特征?
经过化成最简二次根式后,各根式被开放数相同,像这样的几个二次根式被称为同类二次根式.
1. 与最简二次根式 能合并,则 m =_____.
练一练
1
同学们可以说出 的三个同类二次根式?
答案不唯一,如: , , .
二次根式的加减
找同类
二次根式
合并同类二次根式
例如: 2 a + a = (2 + 1) a = 3a
类 比
乘法分配律的逆运用
同理:
+ =
- =
(2 + 1)
(2 - 1)
=
=
思考 现有一块长 7.5 dm、宽 5 dm 的木板,能否采用如图的方式,在这块木板上截出两个分别是 8 dm2 和 18 dm2 的正方形木板?
7.5 dm
5 dm
S=8dm2
S=18dm2
分析:
7.5
大于还是小于
化为最简
二次根式
用分配律合并
整式
加减
二次根
式性质
分配律
整式加
减法则
基本思想:把二次根式加减问题转化为整式加减问题.
归纳总结
思考:如何合并同类二次根式?
合并同类二次根式的方法是:
(1) 化——将非最简二次根式的二次根式化简;
(2) 找——找出被开方数相同的二次根式;
(3) 并——把被开方数相同的二次根式合并.
“一化简二判断三合并”
例1 计算:
典例精析
分析:(1) 一:化简
二:判断
三:合并
(2)
第肆章节
随堂练习
随堂练习
知识点1:二次根式的加减运算
1. 下列式子能与 合并的是( A ).
A. B. C. D.
2. 下列运算正确的是( C )
A. + = B. 3 - =3
C. × = D. ÷ =
A
C
3. 计算.
(1)3 - ; (2)2 + ;
(1)解:原式=(3-1) =2 .
(2)解:原式=4 +3 =7 .
(3) - ; (4) +2 (x≥0).
(3)解:原式=3 - = .
(4)解:原式=2x +2x =4x .
4. 计算.
(1)3 -9 +3 ;
(1)15
(2)( + )+( - ).
(2)6 +
知识点2:二次根式的运用
5. 如图,从一个大正方形中可以裁去面积为8 cm2和32 cm2的两个小正方形,则大正方形的边长为( C ).
A. 2 cm B. 4 cm
C. 6 cm D. 8 cm
(第5题)
C
6. 已知一个三角形的周长为5 cm,一边长为4 cm,另一边长为 cm,求第三边长.
解:第三边长为5 -4 - =35 -16 -5 =14 (cm).
7. 若2 + 可以合并为一项,则m可以是( B ).
A. 6 B. 12 C. 15 D. 18
8. 在二次根式① ,② ,③ ,④ 中,可以与 合并的是( C ).
A. ①② B. ②③ C. ①④ D. ③④
B
C
9. 计算.
(1)3 -4 + ; (2)3 + + - ;
(1)解:原式=15 -12 + =4 .
(2)解:原式=3 +2 +5 -4 =3 -2 +5 .
(3) + -2 ; (4)5 - -2 (a≥0).
(3)解:原式=3 + -2×2 =3 + -4 =0
(4)解:原式=5a-2a-6a=-3a.
10. 如果最简二次根式 与 可以合并.
(1)求a的值.
解:(1)∵最简二次根式 与 可以合并,
∴ 解得a=3.
(2)若a≤x≤2a,化简 + .
(2)将a=3代入a≤x≤2a,得3≤x≤6.
则原式= + = + =x-2+6-x=4.
第伍章节
课堂小结
课堂小结
什么样的二次根式可以合并?二次根式的加减的一般步骤是怎样的?
类比整式的加减
二次整式的加减
化简
合并
计算
应用
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
人教版数学八年级下册
第十六章 二次根式
汇报人:孙老师
汇报班级:X级X班
第1课时 二次根式的加减
16.3 二次根式的加减
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.掌握合并被开方数相同的最简二次根式的方法.
2.熟练运用二次根式的加、减运算法则进行计算.
第贰章节
新课导入
新课导入
化简下列两组二次根式,每组化简后有什么共同特点?
第二组被开方数都是x
第一组被开方数都是3
第叁章节
新知探究
新知探究
整式的加减
找同类项
合并同类项
二次根式的加减
合并同类二次根式
找同类
二次根式
类 比
知识点1:二次根式的加减
例如: 2 a + a =
(2 + 1) a = 3a
?
合作探究
观察下列二次根式有什么共同特征:
每组的二次根式的被开方数相同
下列二次根式又有什么共同特征?
经过化成最简二次根式后,各根式被开放数相同,像这样的几个二次根式被称为同类二次根式.
1. 与最简二次根式 能合并,则 m =_____.
练一练
1
同学们可以说出 的三个同类二次根式?
答案不唯一,如: , , .
二次根式的加减
找同类
二次根式
合并同类二次根式
例如: 2 a + a = (2 + 1) a = 3a
类 比
乘法分配律的逆运用
同理:
+ =
- =
(2 + 1)
(2 - 1)
=
=
思考 现有一块长 7.5 dm、宽 5 dm 的木板,能否采用如图的方式,在这块木板上截出两个分别是 8 dm2 和 18 dm2 的正方形木板?
7.5 dm
5 dm
S=8dm2
S=18dm2
分析:
7.5
大于还是小于
化为最简
二次根式
用分配律合并
整式
加减
二次根
式性质
分配律
整式加
减法则
基本思想:把二次根式加减问题转化为整式加减问题.
归纳总结
思考:如何合并同类二次根式?
合并同类二次根式的方法是:
(1) 化——将非最简二次根式的二次根式化简;
(2) 找——找出被开方数相同的二次根式;
(3) 并——把被开方数相同的二次根式合并.
“一化简二判断三合并”
例1 计算:
典例精析
分析:(1) 一:化简
二:判断
三:合并
(2)
第肆章节
随堂练习
随堂练习
知识点1:二次根式的加减运算
1. 下列式子能与 合并的是( A ).
A. B. C. D.
2. 下列运算正确的是( C )
A. + = B. 3 - =3
C. × = D. ÷ =
A
C
3. 计算.
(1)3 - ; (2)2 + ;
(1)解:原式=(3-1) =2 .
(2)解:原式=4 +3 =7 .
(3) - ; (4) +2 (x≥0).
(3)解:原式=3 - = .
(4)解:原式=2x +2x =4x .
4. 计算.
(1)3 -9 +3 ;
(1)15
(2)( + )+( - ).
(2)6 +
知识点2:二次根式的运用
5. 如图,从一个大正方形中可以裁去面积为8 cm2和32 cm2的两个小正方形,则大正方形的边长为( C ).
A. 2 cm B. 4 cm
C. 6 cm D. 8 cm
(第5题)
C
6. 已知一个三角形的周长为5 cm,一边长为4 cm,另一边长为 cm,求第三边长.
解:第三边长为5 -4 - =35 -16 -5 =14 (cm).
7. 若2 + 可以合并为一项,则m可以是( B ).
A. 6 B. 12 C. 15 D. 18
8. 在二次根式① ,② ,③ ,④ 中,可以与 合并的是( C ).
A. ①② B. ②③ C. ①④ D. ③④
B
C
9. 计算.
(1)3 -4 + ; (2)3 + + - ;
(1)解:原式=15 -12 + =4 .
(2)解:原式=3 +2 +5 -4 =3 -2 +5 .
(3) + -2 ; (4)5 - -2 (a≥0).
(3)解:原式=3 + -2×2 =3 + -4 =0
(4)解:原式=5a-2a-6a=-3a.
10. 如果最简二次根式 与 可以合并.
(1)求a的值.
解:(1)∵最简二次根式 与 可以合并,
∴ 解得a=3.
(2)若a≤x≤2a,化简 + .
(2)将a=3代入a≤x≤2a,得3≤x≤6.
则原式= + = + =x-2+6-x=4.
第伍章节
课堂小结
课堂小结
什么样的二次根式可以合并?二次根式的加减的一般步骤是怎样的?
类比整式的加减
二次整式的加减
化简
合并
计算
应用
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
