人教八下16.2.2 二次根式的除法第2课时 课件(共34张PPT)
文档属性
| 名称 | 人教八下16.2.2 二次根式的除法第2课时 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 12.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 08:59:22 | ||
图片预览









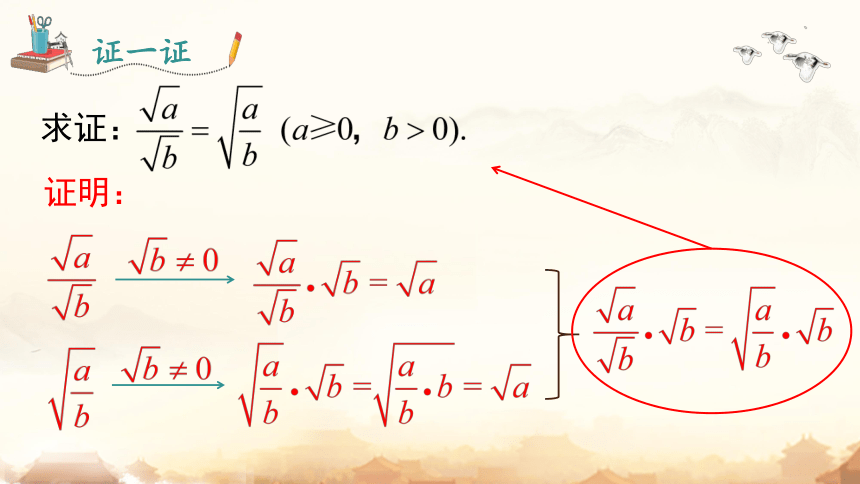

文档简介
(共34张PPT)
人教版数学八年级下册
第十六章 二次根式
汇报人:孙老师
汇报班级:X级X班
第2课时 二次根式的除法
16.2 二次根式的乘除
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.理解并掌握最简二次根式的概念.
2.熟练将二次根式化简为最简二次根式.
第贰章节
新课导入
新课导入
二次根式的乘法法则:
算术平方根的积等于各个被开方数积的算术平方根.
计算
公式逆用:
积的算术平方根,等于积中各因式的算术平方根的积.
化简
第叁章节
新知探究
新知探究
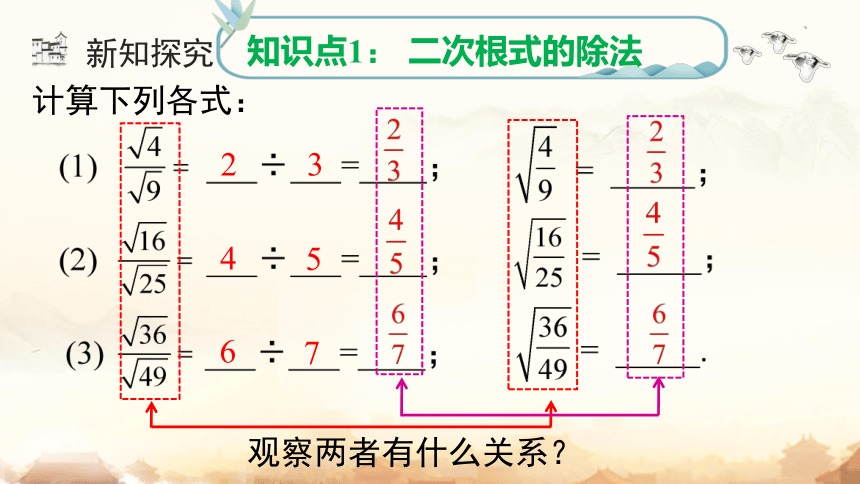
知识点1: 二次根式的除法
计算下列各式:
2
3
4
5
6
7
观察两者有什么关系?
观察三组式子的结果,我们得到下面三个等式:
猜测 你发现了什么规律?能用字母表示你所发现的规律吗?
从上面的猜测的规律中,a,b 的取值范围有没有限制呢?
猜测:
(1)
(2)
(3)
不是的.应该是 a≥0, b>0. 若 b = 0 时,等式两边的二次根式就没有意义啦!
回顾上节课所讲的二次根式的乘法,我们知道
那么对于 是否同样是 a≥0,b≥0?
证一证
求证:
证明:
归纳总结
二次根式的除法法则:
另一种形式:
典例精析
例1 计算:
化简
除法化乘法
分析:(1)
(2)
答案:(1) .
(2) .
练一练
答案:(1) 2 .
(2) 5 .
带分数化假分数
1. 计算:
分析:(3)
解:
(4) 原式
知识点2:商的算术平方根的性质
类比积的算术平方根的性质的由来,
把二次根式的除法法则反过来能得到什么呢?
商的算术平方根的性质
另一种形式:
例2 化简:
分析:(1)
练一练
1. 化简:
带分数化假分数
化分数
解:(1) 原式 =
知识点3:最简二次根式
同学们,观察上面的几道例题,思考在什么情况下二次根式需要化简呢?
二次根式的被开方数中有分数或分式.
二次根式出现在分母当中.
还有被开方数中有未开尽的方的因数或因式.
例3 计算:
分析:
方法二:分母有理化(把分母中的根号化去).
分子与分母同乘一个非零整式,所得分数与原分数相等.
(1)方法一:将二次根式的除法转化为商的算术平方根的形式.
分析:
分析:
归纳总结
满足如下两个特点:
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
我们把满足上述两个条件的二次根式,叫做最简二次根式.
如:
如:
练一练
1. 化简:
解:(1)原式=
(2)原式 =
知识点4:二次根式除法的应用
分析:S = ab
例4 设长方形的面积为 S,相邻两边长分别为 a,b.已知 ,求 a 的值.
代入数值
通过上面的学习,同学们来化简一下新课导入中的问题吧!
第肆章节
随堂练习
随堂练习
知识点1:二次根式的除法法则 = (a≥0,b>0)
1. 计算: = 2 ; ÷ = ; ÷ = (a>0).
2
2
2a
2. 计算: ÷ = (a>0); ÷ = (x≥0,y>0); = 2 (x>0).
2y
2
3. 计算.
(1) ; (2) ÷ .
(1)2 (2)2
4. 计算.
(1) ;
(2) ÷ ;
(1)
(2)
(3) ÷ (x>0,y≥0);
(4) .
(3)2x
(4)2
知识点2:商的算术平方根 = (a≥0,b>0)
5. 化简: = ; = .
6. 化简.
(1) ;
(2) ;
(1)
(2)
(3) (x≥0,y>0);
(4) (x≥0,y>0).
(3)
(4)
知识点3:最简二次根式
7. 下列式子中,是最简二次根式的是( A ).
A. B. C. D.
8. 化简: = ; = ; = ; = .
A
第伍章节
课堂小结
课堂小结
一、二次根式的除法法则:
(a≥0, b>0)
二、最简二次根式特征:
①被开方数不含分母;
②被开方数中不含能开得尽方的因数(或因式);
③分母中不含二次根式.
三、利用商的算术平方根的性质:
(a≥0, b>0)
四、思想方法:
类比思想,转化思想
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
人教版数学八年级下册
第十六章 二次根式
汇报人:孙老师
汇报班级:X级X班
第2课时 二次根式的除法
16.2 二次根式的乘除
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.理解并掌握最简二次根式的概念.
2.熟练将二次根式化简为最简二次根式.
第贰章节
新课导入
新课导入
二次根式的乘法法则:
算术平方根的积等于各个被开方数积的算术平方根.
计算
公式逆用:
积的算术平方根,等于积中各因式的算术平方根的积.
化简
第叁章节
新知探究
新知探究
知识点1: 二次根式的除法
计算下列各式:
2
3
4
5
6
7
观察两者有什么关系?
观察三组式子的结果,我们得到下面三个等式:
猜测 你发现了什么规律?能用字母表示你所发现的规律吗?
从上面的猜测的规律中,a,b 的取值范围有没有限制呢?
猜测:
(1)
(2)
(3)
不是的.应该是 a≥0, b>0. 若 b = 0 时,等式两边的二次根式就没有意义啦!
回顾上节课所讲的二次根式的乘法,我们知道
那么对于 是否同样是 a≥0,b≥0?
证一证
求证:
证明:
归纳总结
二次根式的除法法则:
另一种形式:
典例精析
例1 计算:
化简
除法化乘法
分析:(1)
(2)
答案:(1) .
(2) .
练一练
答案:(1) 2 .
(2) 5 .
带分数化假分数
1. 计算:
分析:(3)
解:
(4) 原式
知识点2:商的算术平方根的性质
类比积的算术平方根的性质的由来,
把二次根式的除法法则反过来能得到什么呢?
商的算术平方根的性质
另一种形式:
例2 化简:
分析:(1)
练一练
1. 化简:
带分数化假分数
化分数
解:(1) 原式 =
知识点3:最简二次根式
同学们,观察上面的几道例题,思考在什么情况下二次根式需要化简呢?
二次根式的被开方数中有分数或分式.
二次根式出现在分母当中.
还有被开方数中有未开尽的方的因数或因式.
例3 计算:
分析:
方法二:分母有理化(把分母中的根号化去).
分子与分母同乘一个非零整式,所得分数与原分数相等.
(1)方法一:将二次根式的除法转化为商的算术平方根的形式.
分析:
分析:
归纳总结
满足如下两个特点:
(1)被开方数不含分母;
(2)被开方数中不含能开得尽方的因数或因式.
我们把满足上述两个条件的二次根式,叫做最简二次根式.
如:
如:
练一练
1. 化简:
解:(1)原式=
(2)原式 =
知识点4:二次根式除法的应用
分析:S = ab
例4 设长方形的面积为 S,相邻两边长分别为 a,b.已知 ,求 a 的值.
代入数值
通过上面的学习,同学们来化简一下新课导入中的问题吧!
第肆章节
随堂练习
随堂练习
知识点1:二次根式的除法法则 = (a≥0,b>0)
1. 计算: = 2 ; ÷ = ; ÷ = (a>0).
2
2
2a
2. 计算: ÷ = (a>0); ÷ = (x≥0,y>0); = 2 (x>0).
2y
2
3. 计算.
(1) ; (2) ÷ .
(1)2 (2)2
4. 计算.
(1) ;
(2) ÷ ;
(1)
(2)
(3) ÷ (x>0,y≥0);
(4) .
(3)2x
(4)2
知识点2:商的算术平方根 = (a≥0,b>0)
5. 化简: = ; = .
6. 化简.
(1) ;
(2) ;
(1)
(2)
(3) (x≥0,y>0);
(4) (x≥0,y>0).
(3)
(4)
知识点3:最简二次根式
7. 下列式子中,是最简二次根式的是( A ).
A. B. C. D.
8. 化简: = ; = ; = ; = .
A
第伍章节
课堂小结
课堂小结
一、二次根式的除法法则:
(a≥0, b>0)
二、最简二次根式特征:
①被开方数不含分母;
②被开方数中不含能开得尽方的因数(或因式);
③分母中不含二次根式.
三、利用商的算术平方根的性质:
(a≥0, b>0)
四、思想方法:
类比思想,转化思想
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
