17.2勾股定理的逆定理第1课时 课件(共29张PPT)
文档属性
| 名称 | 17.2勾股定理的逆定理第1课时 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 12.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 14:11:34 | ||
图片预览







文档简介
(共29张PPT)
人教版数学八年级下册
第十七章 勾股定理
汇报人:孙老师
汇报班级:X级X班
17.2 第1课时 勾股定理的逆定理
17.2 勾股定理的逆定理
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.掌握勾股定理的逆定理概念.
2.熟练运用勾股定理的逆定理去判定直角三角形.
第贰章节
新课导入
新课导入
如果已知三角形的三边长为a,b,c并且满足a2+b2=c2,那么这个三角形是否是直角三角形?
条件:三角形三边a,b,c满足a2+b2=c2.
结论:该三角形是直角三角形.
结论能成立吗
第叁章节
新知探究
新知探究
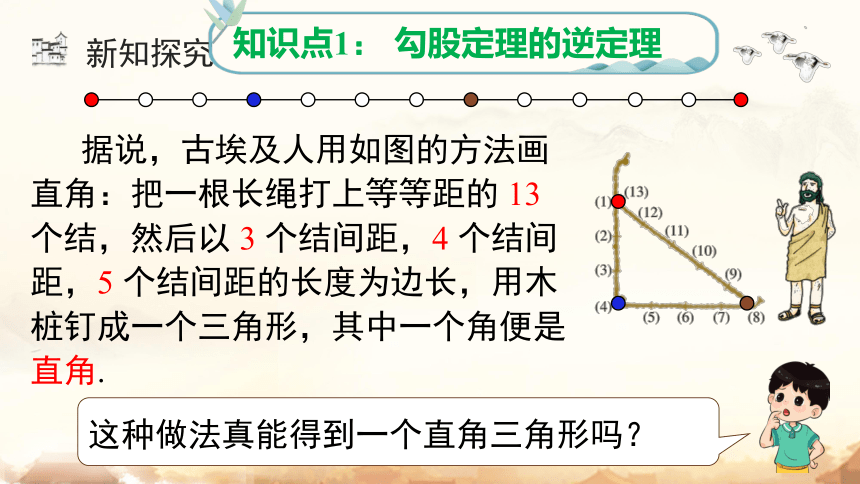
据说,古埃及人用如图的方法画直角:把一根长绳打上等等距的 13 个结,然后以 3 个结间距,4 个结间距,5 个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.
这种做法真能得到一个直角三角形吗?
知识点1: 勾股定理的逆定理
3
4
5
这个三角形三边有什么关系吗?
32 + 42 = 52
画一画
(1) 下列各组数中两个数的平方和等于第三个数的平方,分别以这些数为边长 (单位:cm) 画三角形:
① 2.5,6,6.5; ② 4,7.5,8.5.
(2) 量一量:用量角器分别测量上述各三角形的度数.
2.5
6
6.5
4
7.5
8.5
(3) 想一想:判断这些三角形的形状,提出猜想.
这些三角形是直角三角形!
命题2 如果三角形的三边长 a,b,c 满足 a2 + b2 = c2,那么这个三角形是直角三角形.
猜想
△ABC≌△ A′B′C′
∠C 是直角
△ABC 是直角三角形
A
B
C
a
b
c
构造两直角边分别为a,b 的Rt△A′B′C′
证一证:
已知:如图,△ABC的三边长 a,b,c,满足a2+b2=c2.
求证:△ABC 是直角三角形.
证明:作 Rt△A′B′C′,使∠C′ = 90°,A′C′ = b,B′C′ = a,
∴△ABC≌△A′B′C′(SSS).
∴∠C = ∠C′ = 90°, 即△ABC 是直角三角形.
A
C
a
B
b
c
在△ABC 和△A′B′C′ 中
则 A′B′ 2 = B′C′ 2 + A′C′ 2 = a2 + b2.
∵ a2 + b2 = c2,∴ A′B′ 2 = c2 . ∴ A′B′ = c .
如果三角形的三边长 a 、b 、c 满足
a2 + b2 = c2,
那么这个三角形是直角三角形.
A
C
B
a
b
c
勾股定理的逆定理
这是判定直角三角形的一个依据.
形
数
思维轴
1
找
2
算
3
判
最长边
算出两短边的平方和与最长边的平方
判断等量关系
最长边为斜边,其所对应的角为直角
利用边的关系判断直角三角形
例1 判断由线段 a,b,c 组成的三角形是不是
直角三角形:
典例精析
(1) a = 15,b = 8,c = 17;
(2) a = 13,b = 14,c = 15.
分析:根据勾股定理及其逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
答案:(1) 是直角三角形.
(2) 不是直角三角形.
练一练
1.下列各组线段中,能构成直角三角形的是( )
A.2,3,4 B.3,4,6
C.5,12,13 D.4,6,7
C
2.一个三角形的三边的长分别是 3,4,5,则这个三角形最长边上的高是 ( )
A.4 B.3 C.2.5 D.2.4
D
知识点2: 勾股数
如果三角形的三边长 a,b,c 满足
a2 + b2 = c2,那么这个三角形是直角三角形.
满足 a2 + b2 = c2 的三个正整数,称为勾股数.
常见勾股数:
3,4,5;5,12,13;6,8,10;7,24,25;8,15,17;9,40,41;10,24,26 等等.
勾股数拓展性质:
一组勾股数,都扩大相同倍数 k ( k 为正整数),得到一组新数,这组数同样是勾股数.
如:3,4,5
6,8,10
扩大 2 倍
知识点3: 互逆命题与互逆定理
命题1 如果直角三角形的两条直角边长分别为 a,b,斜边为 c,那么 a2 + b2 = c2.
命题2 如果三角形的三边长 a 、b 、c 满足
a2 + b2 = c2,那么这个三角形是直角三角形.
前面我们学习了两个命题,分别为:
观察两个命题的题设和结论,它们有何联系?
它们是题设和结论正好相反的两个命题.
互逆命题:如果两个命题的题设和结论正好相反,那么这两个命题叫做互逆命题. 如果把其中一个叫做原命题,那么另一个叫做它的逆命题.
归纳总结
互为逆定理:如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,我们称这两个定理互为逆定理.如:勾股定理与勾股定理的逆定理为互逆定理.
注意
(1) 命题有真有假,而定理都是真命题;
(2) 每个命题都有逆命题,但不是所有的定理都有逆定理;
(3) 原命题的真假与其逆命题的真假没有关系.
第肆章节
随堂练习
随堂练习
解析:由,得是直角三角形,且边a的对角是直角,即是直角 .
1.在△中, 的对边分别为a, b , c ,且.
A. 是直角 B. 是直角
C. 是直角 D. 是锐角
C
解析:设直角三角形三边满足a2+b2=c2 ,三边同时扩大3倍后,也满足,所以得到的新三角形还是直角三角形.
2.将直角三角形的三条边同时扩大3倍,得到的三角形是( ).
A. 锐角三角形 B. 等腰三角形
C. 直角三角形 D. 钝角三角形
C
解:因为,所以.
3.已知一个三角形的三边长分别为15,20,25,则这个三角形的面积是多少?
所以这个三角形是直角三角形,且15,20为直角边,则这个三角形的面积为
确定直角边!
第伍章节
课堂小结
课堂小结
勾股定理的逆定理是什么?什么是逆命题?什么样的数叫做勾股数?
勾股定理
互逆命题、
互逆定理
勾股定理的逆定理
直角三角形的判定
证明
内容
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
人教版数学八年级下册
第十七章 勾股定理
汇报人:孙老师
汇报班级:X级X班
17.2 第1课时 勾股定理的逆定理
17.2 勾股定理的逆定理
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.掌握勾股定理的逆定理概念.
2.熟练运用勾股定理的逆定理去判定直角三角形.
第贰章节
新课导入
新课导入
如果已知三角形的三边长为a,b,c并且满足a2+b2=c2,那么这个三角形是否是直角三角形?
条件:三角形三边a,b,c满足a2+b2=c2.
结论:该三角形是直角三角形.
结论能成立吗
第叁章节
新知探究
新知探究
据说,古埃及人用如图的方法画直角:把一根长绳打上等等距的 13 个结,然后以 3 个结间距,4 个结间距,5 个结间距的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.
这种做法真能得到一个直角三角形吗?
知识点1: 勾股定理的逆定理
3
4
5
这个三角形三边有什么关系吗?
32 + 42 = 52
画一画
(1) 下列各组数中两个数的平方和等于第三个数的平方,分别以这些数为边长 (单位:cm) 画三角形:
① 2.5,6,6.5; ② 4,7.5,8.5.
(2) 量一量:用量角器分别测量上述各三角形的度数.
2.5
6
6.5
4
7.5
8.5
(3) 想一想:判断这些三角形的形状,提出猜想.
这些三角形是直角三角形!
命题2 如果三角形的三边长 a,b,c 满足 a2 + b2 = c2,那么这个三角形是直角三角形.
猜想
△ABC≌△ A′B′C′
∠C 是直角
△ABC 是直角三角形
A
B
C
a
b
c
构造两直角边分别为a,b 的Rt△A′B′C′
证一证:
已知:如图,△ABC的三边长 a,b,c,满足a2+b2=c2.
求证:△ABC 是直角三角形.
证明:作 Rt△A′B′C′,使∠C′ = 90°,A′C′ = b,B′C′ = a,
∴△ABC≌△A′B′C′(SSS).
∴∠C = ∠C′ = 90°, 即△ABC 是直角三角形.
A
C
a
B
b
c
在△ABC 和△A′B′C′ 中
则 A′B′ 2 = B′C′ 2 + A′C′ 2 = a2 + b2.
∵ a2 + b2 = c2,∴ A′B′ 2 = c2 . ∴ A′B′ = c .
如果三角形的三边长 a 、b 、c 满足
a2 + b2 = c2,
那么这个三角形是直角三角形.
A
C
B
a
b
c
勾股定理的逆定理
这是判定直角三角形的一个依据.
形
数
思维轴
1
找
2
算
3
判
最长边
算出两短边的平方和与最长边的平方
判断等量关系
最长边为斜边,其所对应的角为直角
利用边的关系判断直角三角形
例1 判断由线段 a,b,c 组成的三角形是不是
直角三角形:
典例精析
(1) a = 15,b = 8,c = 17;
(2) a = 13,b = 14,c = 15.
分析:根据勾股定理及其逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
答案:(1) 是直角三角形.
(2) 不是直角三角形.
练一练
1.下列各组线段中,能构成直角三角形的是( )
A.2,3,4 B.3,4,6
C.5,12,13 D.4,6,7
C
2.一个三角形的三边的长分别是 3,4,5,则这个三角形最长边上的高是 ( )
A.4 B.3 C.2.5 D.2.4
D
知识点2: 勾股数
如果三角形的三边长 a,b,c 满足
a2 + b2 = c2,那么这个三角形是直角三角形.
满足 a2 + b2 = c2 的三个正整数,称为勾股数.
常见勾股数:
3,4,5;5,12,13;6,8,10;7,24,25;8,15,17;9,40,41;10,24,26 等等.
勾股数拓展性质:
一组勾股数,都扩大相同倍数 k ( k 为正整数),得到一组新数,这组数同样是勾股数.
如:3,4,5
6,8,10
扩大 2 倍
知识点3: 互逆命题与互逆定理
命题1 如果直角三角形的两条直角边长分别为 a,b,斜边为 c,那么 a2 + b2 = c2.
命题2 如果三角形的三边长 a 、b 、c 满足
a2 + b2 = c2,那么这个三角形是直角三角形.
前面我们学习了两个命题,分别为:
观察两个命题的题设和结论,它们有何联系?
它们是题设和结论正好相反的两个命题.
互逆命题:如果两个命题的题设和结论正好相反,那么这两个命题叫做互逆命题. 如果把其中一个叫做原命题,那么另一个叫做它的逆命题.
归纳总结
互为逆定理:如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,我们称这两个定理互为逆定理.如:勾股定理与勾股定理的逆定理为互逆定理.
注意
(1) 命题有真有假,而定理都是真命题;
(2) 每个命题都有逆命题,但不是所有的定理都有逆定理;
(3) 原命题的真假与其逆命题的真假没有关系.
第肆章节
随堂练习
随堂练习
解析:由,得是直角三角形,且边a的对角是直角,即是直角 .
1.在△中, 的对边分别为a, b , c ,且.
A. 是直角 B. 是直角
C. 是直角 D. 是锐角
C
解析:设直角三角形三边满足a2+b2=c2 ,三边同时扩大3倍后,也满足,所以得到的新三角形还是直角三角形.
2.将直角三角形的三条边同时扩大3倍,得到的三角形是( ).
A. 锐角三角形 B. 等腰三角形
C. 直角三角形 D. 钝角三角形
C
解:因为,所以.
3.已知一个三角形的三边长分别为15,20,25,则这个三角形的面积是多少?
所以这个三角形是直角三角形,且15,20为直角边,则这个三角形的面积为
确定直角边!
第伍章节
课堂小结
课堂小结
勾股定理的逆定理是什么?什么是逆命题?什么样的数叫做勾股数?
勾股定理
互逆命题、
互逆定理
勾股定理的逆定理
直角三角形的判定
证明
内容
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
