人教八下18.1.2平行四边形的判定第1课时 课件(共37张PPT)
文档属性
| 名称 | 人教八下18.1.2平行四边形的判定第1课时 课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 13:30:25 | ||
图片预览







文档简介
(共37张PPT)
人教版数学八年级下册
第十八章 平行四边形
汇报人:孙老师
汇报班级:X级X班
18.1.2 第1课时 平行四边形的判定(1)
18.1 平行四边形
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1. 平行四边形判定方法1: 两组对边分别 的四边形是平行四边形.
2. 平行四边形判定方法2: 两组对边分别 的四边形是平行四边形.
3. 平行四边形判定方法3: 一组对边 的四边形是平行四边形.
平行
相等
平行且相等
第贰章节
新课导入
新课导入
根据以往几何学习的经验,接下来我们应该研究什么呢?
定义
性质
判定
平行四边形的判定
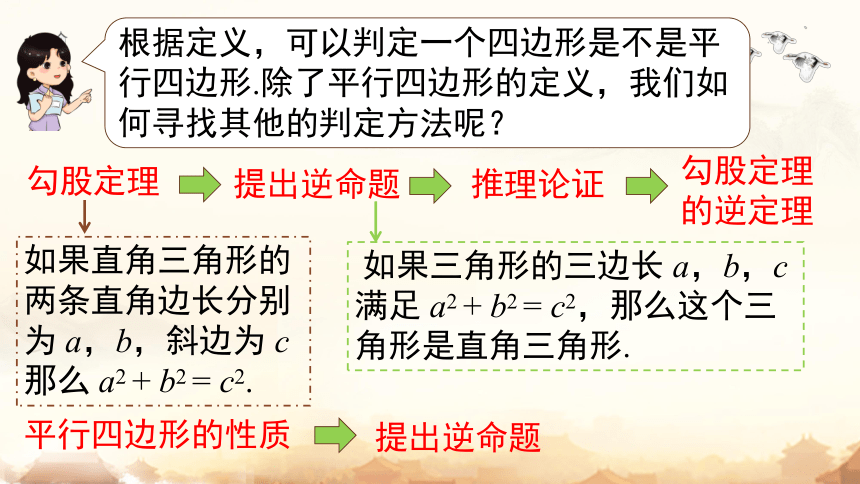
根据定义,可以判定一个四边形是不是平行四边形.除了平行四边形的定义,我们如何寻找其他的判定方法呢?
勾股定理
勾股定理的逆定理
提出逆命题
推理论证
如果直角三角形的两条直角边长分别为 a,b,斜边为 c那么 a2 + b2 = c2.
如果三角形的三边长 a,b,c 满足 a2 + b2 = c2,那么这个三角形是直角三角形.
平行四边形的性质
提出逆命题
平行四边形的性质 逆命题
对边相等
对角相等
对角线互相平分
猜想3:对角线互相平分的四边形是平行四边形
猜想1:两组对边分别相等的四边形是平行四边形
猜想2:两组对角分别相等的四边形是平行四边形
第叁章节
新知探究
新知探究
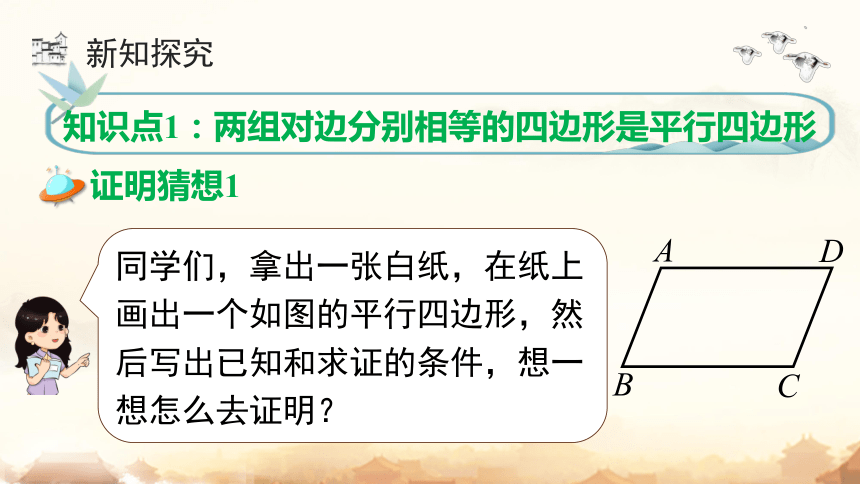
知识点1:两组对边分别相等的四边形是平行四边形
证明猜想1
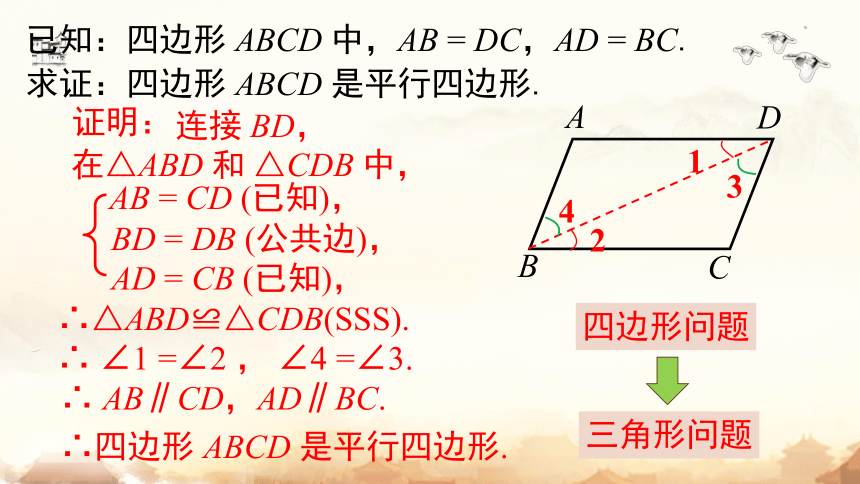
同学们,拿出一张白纸,在纸上画出一个如图的平行四边形,然后写出已知和求证的条件,想一想怎么去证明?
B
D
A
C
B
D
A
C
3
2
4
1
四边形 ABCD 是平行四边形.
已知:
求证:
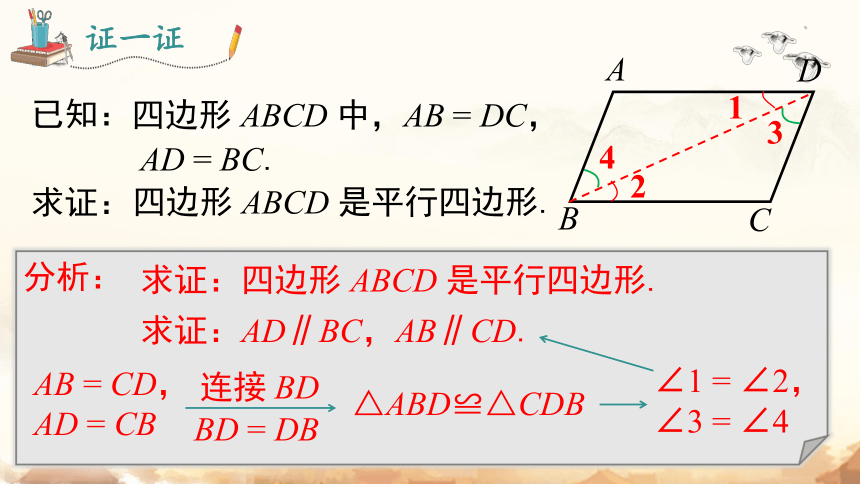
四边形 ABCD 中,AB = DC,
AD = BC.
证一证
分析:
求证:四边形 ABCD 是平行四边形.
求证:AD∥BC,AB∥CD.
AB = CD,AD = CB
△ABD≌△CDB
∠1 = ∠2,∠3 = ∠4
BD = DB
连接 BD
连接 BD,
在△ABD 和 △CDB 中,
AB = CD (已知),
AD = CB (已知),
BD = DB (公共边),
∴△ABD≌△CDB(SSS).
∴ ∠1 =∠2 , ∠4 =∠3.
∴ AB∥CD,AD∥BC.
∴四边形 ABCD 是平行四边形.
证明:
B
D
A
C
3
2
4
1
已知:四边形 ABCD 中,AB = DC,AD = BC.
求证:四边形 ABCD 是平行四边形.
四边形问题
三角形问题
归纳总结
平行四边形的判定定理
两组对边分别相等的四边形是平行四边形.
几何语言描述:
∵ 在四边形 ABCD 中,
AB = CD,AD = CB,
∴ 四边形 ABCD 是平行四边形.
B
D
A
C
练一练
证明:在 Rt△ABC 和 Rt△ADC 中,
AC = CA,
AB = CD,
∴ Rt△ABC≌Rt△CDA(HL).
∴ BC = DA.
又∵ AB = CD,
∴ 四边形 ABCD 是平行四边形.
1. 如图,AD⊥AC,BC⊥AC,且 AB = CD.
求证:四边形 ABCD 是平行四边形.
已知:四边形 ABCD 中,∠A = ∠C,
∠D = ∠B.
求证:四边形 ABCD 是平行四边形.
知识点2:两组对角分别相等的四边形是平行四边形
证明猜想2
B
D
A
C
分析:
∠A = ∠C,∠D = ∠B
∠A + ∠C +∠D + ∠B = 360°
∠A + ∠B = 180°
∠A + ∠D = 180°
AB∥CD,AD∥BC
四边形 ABCD 是平行四边形
已知:四边形 ABCD 中,∠A = ∠C,∠D = ∠B.
求证:四边形 ABCD 是平行四边形.
B
D
A
C
又∵∠A =∠C,∠B =∠D,
∵∠A +∠C +∠B +∠D = 360°,
∴ 2∠A + 2∠B = 360°,
即∠A +∠B = 180°.
∴ AD∥BC.
∴四边形 ABCD 是平行四边形.
同理得 AB∥CD,
证明:
归纳总结
平行四边形的判定定理
两组对角分别相等的四边形是平行四边形.
几何语言描述:
∵ 在四边形 ABCD 中,
∠A =∠C,∠B =∠D,
∴ 四边形 ABCD 是平行四边形.
B
D
A
C
练一练
2. 判断下列四边形是否为平行四边形:
A
D
C
B
110°
70°
110°
A
B
C
D
120°
60°
是
不是
3. 能判定四边形 ABCD 是平行四边形的条件:
∠A∶∠B∶∠C∶∠D 的值为 ( )
A. 1∶2∶3∶4
B. 1∶4∶2∶3
C. 1∶2∶2∶1
D. 3∶2∶3∶2
D
知识点3:对角线互相平分的四边形是平行四边形
证明猜想3
已知:四边形 ABCD 中,AC,BD 相
交点 O, OA = OC,OB = OD.
求证:四边形 ABCD 是平行四边形.
A
B
C
D
O
问题1:上述问题,实际证明什么?
问题2:证明 AD∥BC,AB∥CD,根据平行的判定,利用角的关系进行证明,如何找角的关系?
思考下列问题:
证明 AD∥BC,
AB∥CD
证明:
在△AOB 和△COD 中,
OA = OC (已知),
OB = OD (已知),
∠AOB = ∠COD (对顶角相等),
∴△AOB≌△COD(SAS).
∴ ∠BAO =∠OCD,∠ABO =∠CDO.
∴ AB∥CD , AD∥BC.
∴ 四边形 ABCD 是平行四边形.
已知:四边形 ABCD 中,AC,BD 相交点 O,
OA = OC,OB = OD.
求证:四边形 ABCD 是平行四边形.
A
B
C
D
O
归纳总结
平行四边形的判定定理
对角线互相平分的四边形是平行四边形.
几何语言描述:
∵ 在四边形 ABCD 中,
AO = CO,DO = BO,
∴ 四边形 ABCD 是平行四边形.
A
B
C
D
O
例1 如图, □ABCD 的对角线 AC,BD 相交于点 O,E,F 是 AC 上的两点,并且 AE = CF.
求证:四边形 BFDE 是平行四边形.
B
O
D
A
C
E
F
证明:∵ 四边形 ABCD 是平行四边形,
∴ AO = CO,BO = DO.
∵ AE = CF,
∴ AO -AE = CO - CF,即 EO = OF.
又∵ BO = DO,
∴ 四边形 BFDE 是平行四边形.
典例精析
第肆章节
随堂练习
随堂练习
知识点1:两组对边分别平行的四边形是平行四边形1.如图,在四边形ABCD中,若AB∥CD, BC∥AD,则四边形ABCD为 .
(第1题)
平行四边形
2. 如图,在四边形ABCD中, AB∥CD,当∠A+∠B= ° 时, 四边形ABCD为平行四边形.
(第2题)
180
(第3题)
3. 如图,在四边形ABCD中, 若∠BAC=∠ ,∠DAC=∠ ,则四边形ABCD为平行四边形.
DCA
BCA
知识点2:两组对边分别相等的四边形是平行四边形
4. 在四边形中,有一组对边相等,另一组对边也相等,则这个四边形( A ).
A. 一定是平行四边形
B. 一定不是平行四边形
C. 可以是平行四边形,也可以不是平行四边形
D. 上述答案都不对
A
5. 如图,在四边形ABCD中,AC,BD相交于点O,若AD=8 cm,AB=4 cm,那么当BC= cm,CD= cm时,四边形ABCD为平行四边形.
(第5题)
8
4
知识点3:一组对边平行且相等的四边形是平行四边形
6. 四边形ABCD中,对角线AC,BD相交于点D,下列条件不.能.判定四边形ABCD是平行四边形的是( A ).
A. AD∥BC,AB=CD B. AB∥CD,AB=CD
C. AD∥BC,AB∥CD D. AD=BC,AB=CD
A
7. 在四边形ABCD中,AD∥BC,若AD=8 cm,则当BC= cm时,四边形ABCD为平行四边形.
8
8. 如图,在 ABCD中,点P,Q分别是AD,BC上一点,且∠CDQ=∠ABP.
求证:四边形BQDP是平行四边形.
(第8题)
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,∠A=∠C,AB=CD.
在△ABP和△CDQ中,
∴△ABP≌△CDQ(ASA).∴AP=CQ.
∴AD-AP=BC-CQ,即PD=BQ.
又∵PD∥BQ,
∴四边形BQDP是平行四边形.
9. 如图,在 ABCD中,DE⊥AC,BF⊥AC,垂足分别为E,F.
(第9题)
求证:四边形DEBF为平行四边形.
证明:在 ABCD中,AD=BC,AD∥BC,
∴∠DAC=∠BCA.
又∵∠DEA=∠BFC=90°,
∴Rt△ADE≌Rt△CBF(AAS).∴DE=BF.
又∵DE⊥AC,BF⊥AC,∴DE∥BF.
∴四边形DEBF为平行四边形.
10. 如图,点B,E,C,F在同一条直线上,AB=DE,AB∥DE,BE=CF.
(第10题)
(1)求证:△ABC≌△DEF.
证明:(1)∵AB∥DE,∴∠B=∠DEF.
∵BE=CF,∴BE+CE=CF+CE,即BC=EF.
在△ABC和△DEF中, ∴△ABC≌△DEF(SAS).
在△ABC和△DEF中, ∴△ABC≌△DEF(SAS).
(2)由(1)得△ABC≌△DEF. ∴AC=DF,∠ACB=∠F. ∴AC∥DF.
∴四边形ACFD是平行四边形.
(2)连接AD,求证:四边形ACFD是平行四边形.
11. 如图,在 ABCD中,E,F分别是AB,CD的中点.求证:
(1)△AFD≌△CEB.
(第11题)
证明:(1)在 ABCD中,AD=CB,AB=CD,∠D=∠B.
∵E,F分别是AB,CD的中点,∴DF= CD,BE= AB.
∴DF=BE. ∴△AFD≌△CEB(SAS).
(2)四边形AECF是平行四边形.
(2)在 ABCD中,AB=CD,AB∥CD,∴AE∥CF. 又E,F分别为AB,CD的中点,
∴AE=CF. ∴四边形AECF是平行四边形.
第伍章节
课堂小结
课堂小结
结合本节课的学习,谈谈对研究几何图形判定方法的思考.
定义
判定定理
性质定理
逆向猜想
1
通过本节的学习,我们一共有几种判定平行四边形的方法?
2
在具体证明中,这些方法如何选取?
3
显示总结
显示总结
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
人教版数学八年级下册
第十八章 平行四边形
汇报人:孙老师
汇报班级:X级X班
18.1.2 第1课时 平行四边形的判定(1)
18.1 平行四边形
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1. 平行四边形判定方法1: 两组对边分别 的四边形是平行四边形.
2. 平行四边形判定方法2: 两组对边分别 的四边形是平行四边形.
3. 平行四边形判定方法3: 一组对边 的四边形是平行四边形.
平行
相等
平行且相等
第贰章节
新课导入
新课导入
根据以往几何学习的经验,接下来我们应该研究什么呢?
定义
性质
判定
平行四边形的判定
根据定义,可以判定一个四边形是不是平行四边形.除了平行四边形的定义,我们如何寻找其他的判定方法呢?
勾股定理
勾股定理的逆定理
提出逆命题
推理论证
如果直角三角形的两条直角边长分别为 a,b,斜边为 c那么 a2 + b2 = c2.
如果三角形的三边长 a,b,c 满足 a2 + b2 = c2,那么这个三角形是直角三角形.
平行四边形的性质
提出逆命题
平行四边形的性质 逆命题
对边相等
对角相等
对角线互相平分
猜想3:对角线互相平分的四边形是平行四边形
猜想1:两组对边分别相等的四边形是平行四边形
猜想2:两组对角分别相等的四边形是平行四边形
第叁章节
新知探究
新知探究
知识点1:两组对边分别相等的四边形是平行四边形
证明猜想1
同学们,拿出一张白纸,在纸上画出一个如图的平行四边形,然后写出已知和求证的条件,想一想怎么去证明?
B
D
A
C
B
D
A
C
3
2
4
1
四边形 ABCD 是平行四边形.
已知:
求证:
四边形 ABCD 中,AB = DC,
AD = BC.
证一证
分析:
求证:四边形 ABCD 是平行四边形.
求证:AD∥BC,AB∥CD.
AB = CD,AD = CB
△ABD≌△CDB
∠1 = ∠2,∠3 = ∠4
BD = DB
连接 BD
连接 BD,
在△ABD 和 △CDB 中,
AB = CD (已知),
AD = CB (已知),
BD = DB (公共边),
∴△ABD≌△CDB(SSS).
∴ ∠1 =∠2 , ∠4 =∠3.
∴ AB∥CD,AD∥BC.
∴四边形 ABCD 是平行四边形.
证明:
B
D
A
C
3
2
4
1
已知:四边形 ABCD 中,AB = DC,AD = BC.
求证:四边形 ABCD 是平行四边形.
四边形问题
三角形问题
归纳总结
平行四边形的判定定理
两组对边分别相等的四边形是平行四边形.
几何语言描述:
∵ 在四边形 ABCD 中,
AB = CD,AD = CB,
∴ 四边形 ABCD 是平行四边形.
B
D
A
C
练一练
证明:在 Rt△ABC 和 Rt△ADC 中,
AC = CA,
AB = CD,
∴ Rt△ABC≌Rt△CDA(HL).
∴ BC = DA.
又∵ AB = CD,
∴ 四边形 ABCD 是平行四边形.
1. 如图,AD⊥AC,BC⊥AC,且 AB = CD.
求证:四边形 ABCD 是平行四边形.
已知:四边形 ABCD 中,∠A = ∠C,
∠D = ∠B.
求证:四边形 ABCD 是平行四边形.
知识点2:两组对角分别相等的四边形是平行四边形
证明猜想2
B
D
A
C
分析:
∠A = ∠C,∠D = ∠B
∠A + ∠C +∠D + ∠B = 360°
∠A + ∠B = 180°
∠A + ∠D = 180°
AB∥CD,AD∥BC
四边形 ABCD 是平行四边形
已知:四边形 ABCD 中,∠A = ∠C,∠D = ∠B.
求证:四边形 ABCD 是平行四边形.
B
D
A
C
又∵∠A =∠C,∠B =∠D,
∵∠A +∠C +∠B +∠D = 360°,
∴ 2∠A + 2∠B = 360°,
即∠A +∠B = 180°.
∴ AD∥BC.
∴四边形 ABCD 是平行四边形.
同理得 AB∥CD,
证明:
归纳总结
平行四边形的判定定理
两组对角分别相等的四边形是平行四边形.
几何语言描述:
∵ 在四边形 ABCD 中,
∠A =∠C,∠B =∠D,
∴ 四边形 ABCD 是平行四边形.
B
D
A
C
练一练
2. 判断下列四边形是否为平行四边形:
A
D
C
B
110°
70°
110°
A
B
C
D
120°
60°
是
不是
3. 能判定四边形 ABCD 是平行四边形的条件:
∠A∶∠B∶∠C∶∠D 的值为 ( )
A. 1∶2∶3∶4
B. 1∶4∶2∶3
C. 1∶2∶2∶1
D. 3∶2∶3∶2
D
知识点3:对角线互相平分的四边形是平行四边形
证明猜想3
已知:四边形 ABCD 中,AC,BD 相
交点 O, OA = OC,OB = OD.
求证:四边形 ABCD 是平行四边形.
A
B
C
D
O
问题1:上述问题,实际证明什么?
问题2:证明 AD∥BC,AB∥CD,根据平行的判定,利用角的关系进行证明,如何找角的关系?
思考下列问题:
证明 AD∥BC,
AB∥CD
证明:
在△AOB 和△COD 中,
OA = OC (已知),
OB = OD (已知),
∠AOB = ∠COD (对顶角相等),
∴△AOB≌△COD(SAS).
∴ ∠BAO =∠OCD,∠ABO =∠CDO.
∴ AB∥CD , AD∥BC.
∴ 四边形 ABCD 是平行四边形.
已知:四边形 ABCD 中,AC,BD 相交点 O,
OA = OC,OB = OD.
求证:四边形 ABCD 是平行四边形.
A
B
C
D
O
归纳总结
平行四边形的判定定理
对角线互相平分的四边形是平行四边形.
几何语言描述:
∵ 在四边形 ABCD 中,
AO = CO,DO = BO,
∴ 四边形 ABCD 是平行四边形.
A
B
C
D
O
例1 如图, □ABCD 的对角线 AC,BD 相交于点 O,E,F 是 AC 上的两点,并且 AE = CF.
求证:四边形 BFDE 是平行四边形.
B
O
D
A
C
E
F
证明:∵ 四边形 ABCD 是平行四边形,
∴ AO = CO,BO = DO.
∵ AE = CF,
∴ AO -AE = CO - CF,即 EO = OF.
又∵ BO = DO,
∴ 四边形 BFDE 是平行四边形.
典例精析
第肆章节
随堂练习
随堂练习
知识点1:两组对边分别平行的四边形是平行四边形1.如图,在四边形ABCD中,若AB∥CD, BC∥AD,则四边形ABCD为 .
(第1题)
平行四边形
2. 如图,在四边形ABCD中, AB∥CD,当∠A+∠B= ° 时, 四边形ABCD为平行四边形.
(第2题)
180
(第3题)
3. 如图,在四边形ABCD中, 若∠BAC=∠ ,∠DAC=∠ ,则四边形ABCD为平行四边形.
DCA
BCA
知识点2:两组对边分别相等的四边形是平行四边形
4. 在四边形中,有一组对边相等,另一组对边也相等,则这个四边形( A ).
A. 一定是平行四边形
B. 一定不是平行四边形
C. 可以是平行四边形,也可以不是平行四边形
D. 上述答案都不对
A
5. 如图,在四边形ABCD中,AC,BD相交于点O,若AD=8 cm,AB=4 cm,那么当BC= cm,CD= cm时,四边形ABCD为平行四边形.
(第5题)
8
4
知识点3:一组对边平行且相等的四边形是平行四边形
6. 四边形ABCD中,对角线AC,BD相交于点D,下列条件不.能.判定四边形ABCD是平行四边形的是( A ).
A. AD∥BC,AB=CD B. AB∥CD,AB=CD
C. AD∥BC,AB∥CD D. AD=BC,AB=CD
A
7. 在四边形ABCD中,AD∥BC,若AD=8 cm,则当BC= cm时,四边形ABCD为平行四边形.
8
8. 如图,在 ABCD中,点P,Q分别是AD,BC上一点,且∠CDQ=∠ABP.
求证:四边形BQDP是平行四边形.
(第8题)
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,∠A=∠C,AB=CD.
在△ABP和△CDQ中,
∴△ABP≌△CDQ(ASA).∴AP=CQ.
∴AD-AP=BC-CQ,即PD=BQ.
又∵PD∥BQ,
∴四边形BQDP是平行四边形.
9. 如图,在 ABCD中,DE⊥AC,BF⊥AC,垂足分别为E,F.
(第9题)
求证:四边形DEBF为平行四边形.
证明:在 ABCD中,AD=BC,AD∥BC,
∴∠DAC=∠BCA.
又∵∠DEA=∠BFC=90°,
∴Rt△ADE≌Rt△CBF(AAS).∴DE=BF.
又∵DE⊥AC,BF⊥AC,∴DE∥BF.
∴四边形DEBF为平行四边形.
10. 如图,点B,E,C,F在同一条直线上,AB=DE,AB∥DE,BE=CF.
(第10题)
(1)求证:△ABC≌△DEF.
证明:(1)∵AB∥DE,∴∠B=∠DEF.
∵BE=CF,∴BE+CE=CF+CE,即BC=EF.
在△ABC和△DEF中, ∴△ABC≌△DEF(SAS).
在△ABC和△DEF中, ∴△ABC≌△DEF(SAS).
(2)由(1)得△ABC≌△DEF. ∴AC=DF,∠ACB=∠F. ∴AC∥DF.
∴四边形ACFD是平行四边形.
(2)连接AD,求证:四边形ACFD是平行四边形.
11. 如图,在 ABCD中,E,F分别是AB,CD的中点.求证:
(1)△AFD≌△CEB.
(第11题)
证明:(1)在 ABCD中,AD=CB,AB=CD,∠D=∠B.
∵E,F分别是AB,CD的中点,∴DF= CD,BE= AB.
∴DF=BE. ∴△AFD≌△CEB(SAS).
(2)四边形AECF是平行四边形.
(2)在 ABCD中,AB=CD,AB∥CD,∴AE∥CF. 又E,F分别为AB,CD的中点,
∴AE=CF. ∴四边形AECF是平行四边形.
第伍章节
课堂小结
课堂小结
结合本节课的学习,谈谈对研究几何图形判定方法的思考.
定义
判定定理
性质定理
逆向猜想
1
通过本节的学习,我们一共有几种判定平行四边形的方法?
2
在具体证明中,这些方法如何选取?
3
显示总结
显示总结
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
