人教八下18.2.1矩形的性质第1课时 课件(共38张PPT)
文档属性
| 名称 | 人教八下18.2.1矩形的性质第1课时 课件(共38张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 00:00:00 | ||
图片预览









文档简介
(共38张PPT)
人教版数学八年级下册
第十八章 平行四边形
汇报人:孙老师
汇报班级:X级X班
18.2.1 第1课时 矩形的性质
18.2 特殊的平行四边形
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.掌握矩形的概念,能比较与平行四边形的异同.
2.探索并证明矩形的性质,会用矩形的性质解决问题.
第贰章节
新课导入
新课导入
拿一个活动的平行四边形教具,轻轻拉动一个点,它还是平行四边形吗 使一个角是直角,这时它是什么图形
点击查看平行四边形到矩形的变化过程
平行四边形
一个角是直角
矩形的概念:有一个角是直角的平行四边形叫做矩形,也就是长方形.
仔细观察下列实际生活中的图片,你觉得哪些是矩形的形象
矩形是生活中很常见的图形,你还能列举出矩形在生活中应用的其他例子吗
我们一起来探讨一下矩形的性质吧!
第叁章节
新知探究
新知探究
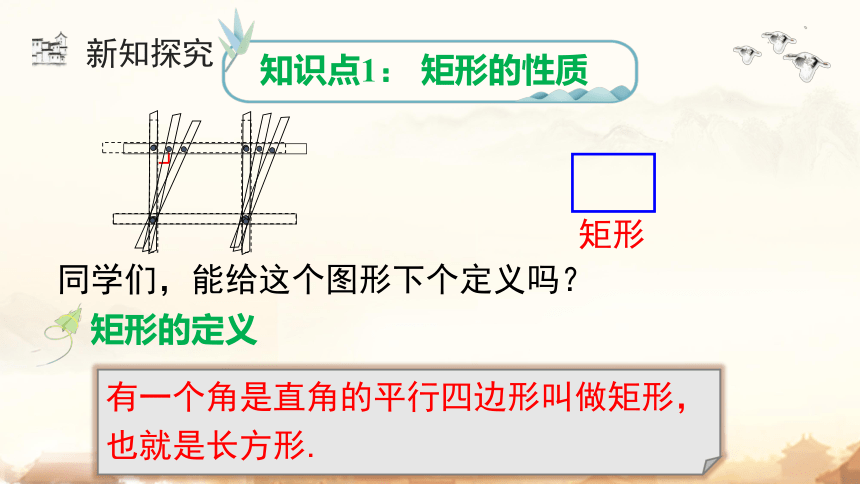
知识点1: 矩形的性质
矩形
同学们,能给这个图形下个定义吗?
矩形的定义
有一个角是直角的平行四边形叫做矩形,
也就是长方形.
矩形也是常见的图形,能否举出生活中矩形形象的例子?
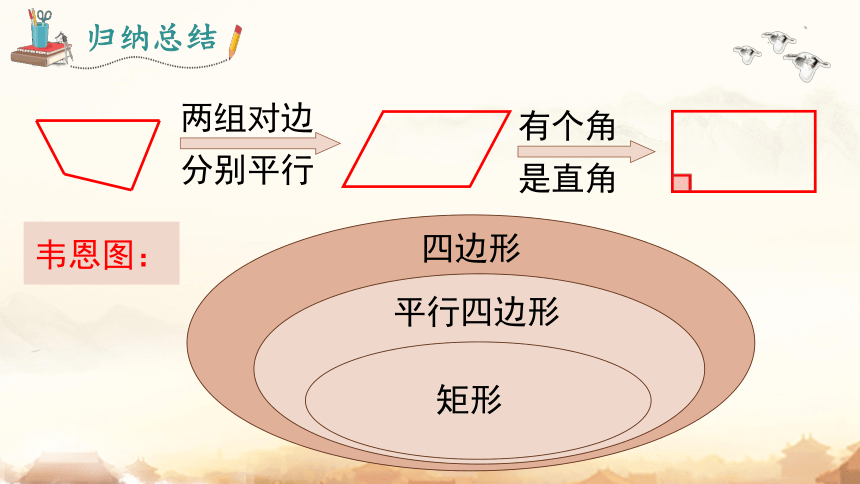
两组对边分别平行
有个角是直角
四边形
平行四边形
矩形
归纳总结
韦恩图:
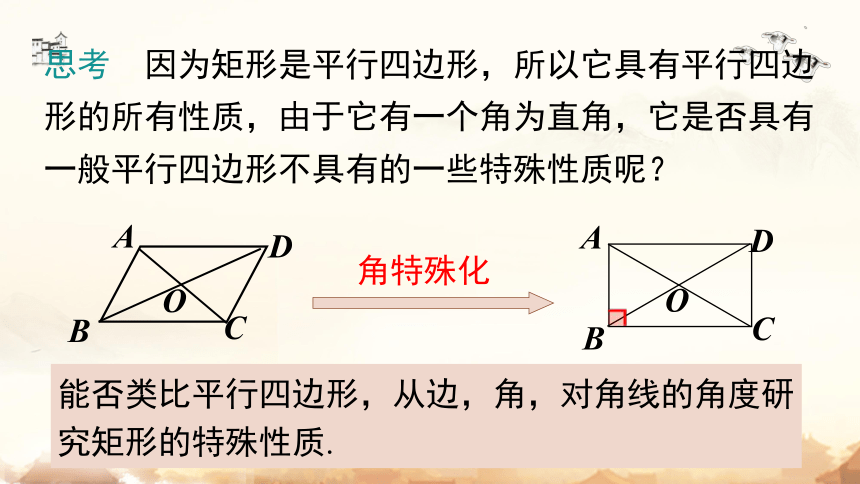
思考 因为矩形是平行四边形,所以它具有平行四边形的所有性质,由于它有一个角为直角,它是否具有一般平行四边形不具有的一些特殊性质呢?
能否类比平行四边形,从边,角,对角线的角度研究矩形的特殊性质.
A
B
C
D
O
A
B
C
D
O
角特殊化
活动:
准备素材:直尺、量角器、橡皮擦、课本、铅笔盒等.
(1) 请同学们以小组为单位,测量身边的矩形 (如书本,课桌,铅笔盒等) 的四条边的长度、四个角的度数和对角线的长度及夹角度数,并记录测量结果.
A
B
C
D
O
AB AD AC BD ∠BAD ∠ADC ∠AOD ∠AOB
橡皮擦
课本
桌子
物体
测量
(实物)
(形象图)
(2) 根据测量的结果,你有什么猜想?
猜想1 矩形的四个角都是直角.
猜想2 矩形的对角线相等.
你能证明吗?
证一证
证明:∵四边形 ABCD 是矩形,
∴∠B =∠D,∠C =∠A,AB∥DC.
∴∠B +∠C = 180°.
又∵∠B = 90°,
∴∠C = 90°.
∴∠B =∠C =∠D =∠A = 90°.
(1) 如图,四边形 ABCD 是矩形,∠B = 90°.
求证:∠B =∠C =∠D =∠A = 90°.
A
B
C
D
(2) 如图,四边形 ABCD 是矩形,
∠ABC = 90°,对角线 AC 与 DB 相交于点 O. 求证:AC = DB.
A
B
C
D
O
分析:
逆向思维
求证:AC = DB
求证:△ABC≌△DCB
正向思维
四边形 ABCD 是矩形
AB = DC,
∠ABC =∠DCB = 90°
△ABC≌△DCB
证明:∵ 四边形 ABCD 是矩形,
∴ AB = DC,∠ABC =∠DCB = 90°,
在 △ABC 和 △DCB 中,
∵ AB = DC,∠ABC = ∠DCB,BC = CB,
∴ △ABC≌△DCB.
∴ AC = DB.
A
B
C
D
O
(2) 如图,四边形 ABCD 是矩形,∠ABC = 90°,对角线 AC 与 DB 相交于点 O. 求证:AC = DB.
归纳总结
角:
对角线:
矩形的性质
对边平行相等;对角相等;对角线相互平分.
矩形的四个角都是直角
矩形的对角线相等
几何语言描述:
∵ 四边形 ABCD 是矩形,
∴ ∠ABC =∠BCD =∠DCA = ∠DAB = 90°,
AC = BD.
A
B
C
D
O
证明:连接 DE.
∵AD = AE,∴∠AED =∠ADE.
∵ 四边形 ABCD 是矩形,
∴ AD∥BC,∠C = 90°.
∴∠ADE =∠CED.
∴∠CED =∠AED.
又∵ DF⊥AE,
∴ DF = DC.
1. 如图,在矩形 ABCD 中,E 是 BC 上的点,AE = AD,
DF⊥AE,垂足为 F. 求证:DF = DC.
A
B
C
D
E
F
练一练
思考 请同学们拿出准备好的矩形纸片,折一折,观察并思考. 矩形是不是轴对称图形 如果是,那么对称轴有几条
矩形的性质:
对称性: 图形,对称轴: 条.
轴对称
2
练一练
2. 如图,在矩形 ABCD 中,对角线 AC,BD 交于
点 O,下列说法错误的是 ( )
A.AB∥DC B.AC = BD
C.AC⊥BD D.OA = OB
A
B
C
D
O
C
3. 如图,EF 过矩形 ABCD 对角线的交点 O,且分别交 AB、CD 于 E、F,那么阴影部分的面积是矩形ABCD 面积的_________.
知识点2:直角三角形斜边上的中线的性质
A
B
C
D
O
活动:如图,一张矩形纸片,画出两条对角线,沿着对角线 AC 剪去一半.
B
C
O
A
问题 Rt△ABC 中,BO 是一条怎样的线段?
它的长度与斜边 AC 有什么关系?
猜想:直角三角形斜边上的中线等于斜边的一半.
试给出数学证明.
证明:延长 BO 至 D,使 OD = BO,
连接 AD,CD.
∵ AO = OC,BO = OD,
∴ 四边形 ABCD 是平行四边形.
∵∠ABC = 90°,
∴ 平行四边形 ABCD 是矩形.
∴ AC = BD.
如图,在 Rt△ABC 中,∠ABC = 90°,BO 是 AC 上的中线. 求证:BO = AC.
O
C
B
A
D
证一证
∴ BO = BD = AC.
练一练
4. 如图,在△ABC 中,∠ABC = 90°,BD 是斜边 AC 上的中线.
(1)若 BD = 3 cm,则 AC =_____cm;
(2)若∠C = 30°,AB = 5 cm,则 AC =_____cm,
BD = _____cm.
A
B
C
D
6
10
5
第肆章节
随堂练习
随堂练习
知识点1:矩形的四个角都是直角
1. 如图,矩形ABCD中AC交BD于点O,∠AOB=105°,则∠ODC的度数为 .
2. 在矩形ABCD中,AB=3,BC=4,则AC= ,矩形的面积为 .
3. 已知一个矩形长3 cm,宽2 cm,则它的对角线长 cm.
37.5°
5
12
(1)△ADM≌△BCM.
(第4题)
证明:(1)∵四边形ABCD是矩形,
∴∠ADM=∠BCM,AD=BC.
∵M是CD的中点,∴DM=CM.
∴△ADM≌△BCM(SAS).
4. 如图,在矩形ABCD中,M是CD的中点.求证:
(2)∠MAB=∠MBA.
(2)由(1)得△ADM≌△BCM,∴MA=MB.
∴∠MAB=∠MBA.
知识点2:矩形的对角线相等且互相平分
5. 矩形具有而一般平行四边形不.具.有.的性质是( C ).
A. 对角线互相平分 B. 邻角互补
C. 对角线相等 D. 对角相等
C
6. 如图,矩形ABCD的对角线AC和BD相交于点O,若AO=5,则BD= .
(第6题)
10
7. 如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AB= cm,则矩形对角线AC长为 2 cm.
(第7题)
2
知识点3:直角三角形斜边上的中线等于斜边的一半8.在Rt△ABC中,∠ACB=90°,AC=6,BC=8,D为AB的中点,则CD= .
(第8题)
5
(第9题)
9. 如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,CD=3,AC=2,则BC的长为( D ).
A. 3 B. 4 C. 6 D. 4
D
10. 矩形ABCD的两条对角线AC,BD相交于点O,∠AOB=60°,OA=3,则AC= ,AB= .
6
3
11. 如图,平面直角坐标系中,长方形OABC的顶点O为坐标原点,顶点A(0,2),顶点B在第二象限.若长方形OABC的面积为6,则点B的坐标为( A ).
A. (-3,2) B. (-2,3)
C. (3,2) D. (-3,-2)
A
12. 如图,对角线AC,BD交于点O,M是AD中点,连接OM. 若OM=3,BC=10,则OB的长为( D ).
A. 5 B. 4 C. D.
(第12题)
D
13. 如图,在Rt△ABC中,∠BAC=90°,D,E,F分别是三边的中点,且DE=4,求AF的长度.
(第13题)
解:∵D,E分别为AB,AC的中点,
∴DE∥BC,BC=2DE=8.
∵F为BC的中点,
∴AF是直角三角形斜边上的中线.
∴AF= BC=4.
14. 如图,矩形ABCD的对角线AC,BD相交于点O,AE平分∠BAD,∠AOD=120°.
(第14题)
求∠OAE的度数.
解:∵四边形ABCD是矩形,
∴OA= AC= BD=OD,∠BAD=90°.
∵∠AOD=120°,∴∠OAD=∠ODA=30°.
∵AE平分∠BAD,∴∠BAE=∠DAE=45°.
∴∠OAE=∠DAE-∠OAD=15°.
第伍章节
课堂小结
课堂小结
矩形的概念:
矩形的性质:
直角三角形斜边上的中线的性质:
有一个角是直角的平行四边形叫做矩形.
矩形的四个角都是直角;
矩形的对角线相等.
直角三角形斜边上的中线等于斜边的一半.
知识结构
平行
四边形
矩形
性质:边、角、对角线
转化:直角三角形、等腰三角形
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
人教版数学八年级下册
第十八章 平行四边形
汇报人:孙老师
汇报班级:X级X班
18.2.1 第1课时 矩形的性质
18.2 特殊的平行四边形
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.掌握矩形的概念,能比较与平行四边形的异同.
2.探索并证明矩形的性质,会用矩形的性质解决问题.
第贰章节
新课导入
新课导入
拿一个活动的平行四边形教具,轻轻拉动一个点,它还是平行四边形吗 使一个角是直角,这时它是什么图形
点击查看平行四边形到矩形的变化过程
平行四边形
一个角是直角
矩形的概念:有一个角是直角的平行四边形叫做矩形,也就是长方形.
仔细观察下列实际生活中的图片,你觉得哪些是矩形的形象
矩形是生活中很常见的图形,你还能列举出矩形在生活中应用的其他例子吗
我们一起来探讨一下矩形的性质吧!
第叁章节
新知探究
新知探究
知识点1: 矩形的性质
矩形
同学们,能给这个图形下个定义吗?
矩形的定义
有一个角是直角的平行四边形叫做矩形,
也就是长方形.
矩形也是常见的图形,能否举出生活中矩形形象的例子?
两组对边分别平行
有个角是直角
四边形
平行四边形
矩形
归纳总结
韦恩图:
思考 因为矩形是平行四边形,所以它具有平行四边形的所有性质,由于它有一个角为直角,它是否具有一般平行四边形不具有的一些特殊性质呢?
能否类比平行四边形,从边,角,对角线的角度研究矩形的特殊性质.
A
B
C
D
O
A
B
C
D
O
角特殊化
活动:
准备素材:直尺、量角器、橡皮擦、课本、铅笔盒等.
(1) 请同学们以小组为单位,测量身边的矩形 (如书本,课桌,铅笔盒等) 的四条边的长度、四个角的度数和对角线的长度及夹角度数,并记录测量结果.
A
B
C
D
O
AB AD AC BD ∠BAD ∠ADC ∠AOD ∠AOB
橡皮擦
课本
桌子
物体
测量
(实物)
(形象图)
(2) 根据测量的结果,你有什么猜想?
猜想1 矩形的四个角都是直角.
猜想2 矩形的对角线相等.
你能证明吗?
证一证
证明:∵四边形 ABCD 是矩形,
∴∠B =∠D,∠C =∠A,AB∥DC.
∴∠B +∠C = 180°.
又∵∠B = 90°,
∴∠C = 90°.
∴∠B =∠C =∠D =∠A = 90°.
(1) 如图,四边形 ABCD 是矩形,∠B = 90°.
求证:∠B =∠C =∠D =∠A = 90°.
A
B
C
D
(2) 如图,四边形 ABCD 是矩形,
∠ABC = 90°,对角线 AC 与 DB 相交于点 O. 求证:AC = DB.
A
B
C
D
O
分析:
逆向思维
求证:AC = DB
求证:△ABC≌△DCB
正向思维
四边形 ABCD 是矩形
AB = DC,
∠ABC =∠DCB = 90°
△ABC≌△DCB
证明:∵ 四边形 ABCD 是矩形,
∴ AB = DC,∠ABC =∠DCB = 90°,
在 △ABC 和 △DCB 中,
∵ AB = DC,∠ABC = ∠DCB,BC = CB,
∴ △ABC≌△DCB.
∴ AC = DB.
A
B
C
D
O
(2) 如图,四边形 ABCD 是矩形,∠ABC = 90°,对角线 AC 与 DB 相交于点 O. 求证:AC = DB.
归纳总结
角:
对角线:
矩形的性质
对边平行相等;对角相等;对角线相互平分.
矩形的四个角都是直角
矩形的对角线相等
几何语言描述:
∵ 四边形 ABCD 是矩形,
∴ ∠ABC =∠BCD =∠DCA = ∠DAB = 90°,
AC = BD.
A
B
C
D
O
证明:连接 DE.
∵AD = AE,∴∠AED =∠ADE.
∵ 四边形 ABCD 是矩形,
∴ AD∥BC,∠C = 90°.
∴∠ADE =∠CED.
∴∠CED =∠AED.
又∵ DF⊥AE,
∴ DF = DC.
1. 如图,在矩形 ABCD 中,E 是 BC 上的点,AE = AD,
DF⊥AE,垂足为 F. 求证:DF = DC.
A
B
C
D
E
F
练一练
思考 请同学们拿出准备好的矩形纸片,折一折,观察并思考. 矩形是不是轴对称图形 如果是,那么对称轴有几条
矩形的性质:
对称性: 图形,对称轴: 条.
轴对称
2
练一练
2. 如图,在矩形 ABCD 中,对角线 AC,BD 交于
点 O,下列说法错误的是 ( )
A.AB∥DC B.AC = BD
C.AC⊥BD D.OA = OB
A
B
C
D
O
C
3. 如图,EF 过矩形 ABCD 对角线的交点 O,且分别交 AB、CD 于 E、F,那么阴影部分的面积是矩形ABCD 面积的_________.
知识点2:直角三角形斜边上的中线的性质
A
B
C
D
O
活动:如图,一张矩形纸片,画出两条对角线,沿着对角线 AC 剪去一半.
B
C
O
A
问题 Rt△ABC 中,BO 是一条怎样的线段?
它的长度与斜边 AC 有什么关系?
猜想:直角三角形斜边上的中线等于斜边的一半.
试给出数学证明.
证明:延长 BO 至 D,使 OD = BO,
连接 AD,CD.
∵ AO = OC,BO = OD,
∴ 四边形 ABCD 是平行四边形.
∵∠ABC = 90°,
∴ 平行四边形 ABCD 是矩形.
∴ AC = BD.
如图,在 Rt△ABC 中,∠ABC = 90°,BO 是 AC 上的中线. 求证:BO = AC.
O
C
B
A
D
证一证
∴ BO = BD = AC.
练一练
4. 如图,在△ABC 中,∠ABC = 90°,BD 是斜边 AC 上的中线.
(1)若 BD = 3 cm,则 AC =_____cm;
(2)若∠C = 30°,AB = 5 cm,则 AC =_____cm,
BD = _____cm.
A
B
C
D
6
10
5
第肆章节
随堂练习
随堂练习
知识点1:矩形的四个角都是直角
1. 如图,矩形ABCD中AC交BD于点O,∠AOB=105°,则∠ODC的度数为 .
2. 在矩形ABCD中,AB=3,BC=4,则AC= ,矩形的面积为 .
3. 已知一个矩形长3 cm,宽2 cm,则它的对角线长 cm.
37.5°
5
12
(1)△ADM≌△BCM.
(第4题)
证明:(1)∵四边形ABCD是矩形,
∴∠ADM=∠BCM,AD=BC.
∵M是CD的中点,∴DM=CM.
∴△ADM≌△BCM(SAS).
4. 如图,在矩形ABCD中,M是CD的中点.求证:
(2)∠MAB=∠MBA.
(2)由(1)得△ADM≌△BCM,∴MA=MB.
∴∠MAB=∠MBA.
知识点2:矩形的对角线相等且互相平分
5. 矩形具有而一般平行四边形不.具.有.的性质是( C ).
A. 对角线互相平分 B. 邻角互补
C. 对角线相等 D. 对角相等
C
6. 如图,矩形ABCD的对角线AC和BD相交于点O,若AO=5,则BD= .
(第6题)
10
7. 如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°,AB= cm,则矩形对角线AC长为 2 cm.
(第7题)
2
知识点3:直角三角形斜边上的中线等于斜边的一半8.在Rt△ABC中,∠ACB=90°,AC=6,BC=8,D为AB的中点,则CD= .
(第8题)
5
(第9题)
9. 如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,CD=3,AC=2,则BC的长为( D ).
A. 3 B. 4 C. 6 D. 4
D
10. 矩形ABCD的两条对角线AC,BD相交于点O,∠AOB=60°,OA=3,则AC= ,AB= .
6
3
11. 如图,平面直角坐标系中,长方形OABC的顶点O为坐标原点,顶点A(0,2),顶点B在第二象限.若长方形OABC的面积为6,则点B的坐标为( A ).
A. (-3,2) B. (-2,3)
C. (3,2) D. (-3,-2)
A
12. 如图,对角线AC,BD交于点O,M是AD中点,连接OM. 若OM=3,BC=10,则OB的长为( D ).
A. 5 B. 4 C. D.
(第12题)
D
13. 如图,在Rt△ABC中,∠BAC=90°,D,E,F分别是三边的中点,且DE=4,求AF的长度.
(第13题)
解:∵D,E分别为AB,AC的中点,
∴DE∥BC,BC=2DE=8.
∵F为BC的中点,
∴AF是直角三角形斜边上的中线.
∴AF= BC=4.
14. 如图,矩形ABCD的对角线AC,BD相交于点O,AE平分∠BAD,∠AOD=120°.
(第14题)
求∠OAE的度数.
解:∵四边形ABCD是矩形,
∴OA= AC= BD=OD,∠BAD=90°.
∵∠AOD=120°,∴∠OAD=∠ODA=30°.
∵AE平分∠BAD,∴∠BAE=∠DAE=45°.
∴∠OAE=∠DAE-∠OAD=15°.
第伍章节
课堂小结
课堂小结
矩形的概念:
矩形的性质:
直角三角形斜边上的中线的性质:
有一个角是直角的平行四边形叫做矩形.
矩形的四个角都是直角;
矩形的对角线相等.
直角三角形斜边上的中线等于斜边的一半.
知识结构
平行
四边形
矩形
性质:边、角、对角线
转化:直角三角形、等腰三角形
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
