人教八下18.1.2平行四边形的判定第2课时 课件(共33张PPT)
文档属性
| 名称 | 人教八下18.1.2平行四边形的判定第2课时 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 15.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 13:37:38 | ||
图片预览








文档简介
(共33张PPT)
人教版数学八年级下册
第十八章 平行四边形
汇报人:孙老师
汇报班级:X级X班
18.1.2 第2课时 平行四边形的判定(2)
18.1 平行四边形
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1. 平行四边形判定方法4:对角线 的四边形是平行四边形.
2. 平行四边形判定方法5:两组对角 的四边形是平行四边形.
互相平分
分别相等
第贰章节
新课导入
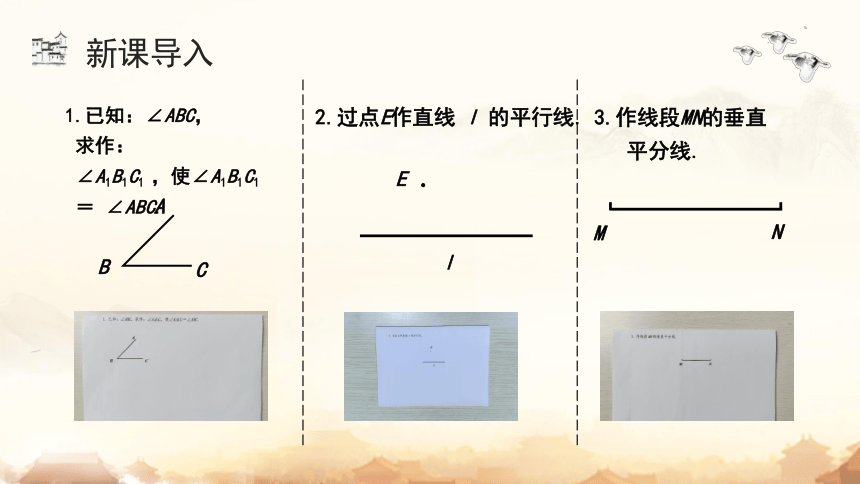
新课导入
求作:
∠A1B1C1 ,使∠A1B1C1
= ∠ABC.
1.已知:∠ABC,
A
B
C
3.作线段MN的垂直
平分线.
2.过点E作直线 l 的平行线.
l
E
M
N
第叁章节
新知探究
新知探究
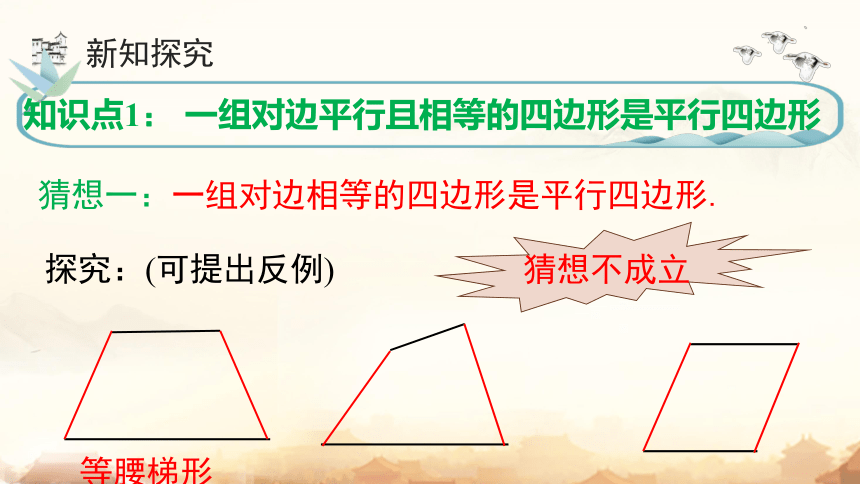
知识点1: 一组对边平行且相等的四边形是平行四边形
探究:(可提出反例)
猜想一:一组对边相等的四边形是平行四边形.
等腰梯形
猜想不成立
探究:(可提出反例)
猜想二:一组对边平行的四边形是平行四边形.
猜想不成立
梯形
猜想三:一组对边平行且相等的四边形是平行四边形.
同学们,拿出一张白纸,在纸上画出一个平行四边形,然后写出已知和求证的条件,想一想怎么去证明?
B
D
A
C
B
D
A
C
2
1
四边形 ABCD 是平行四边形.
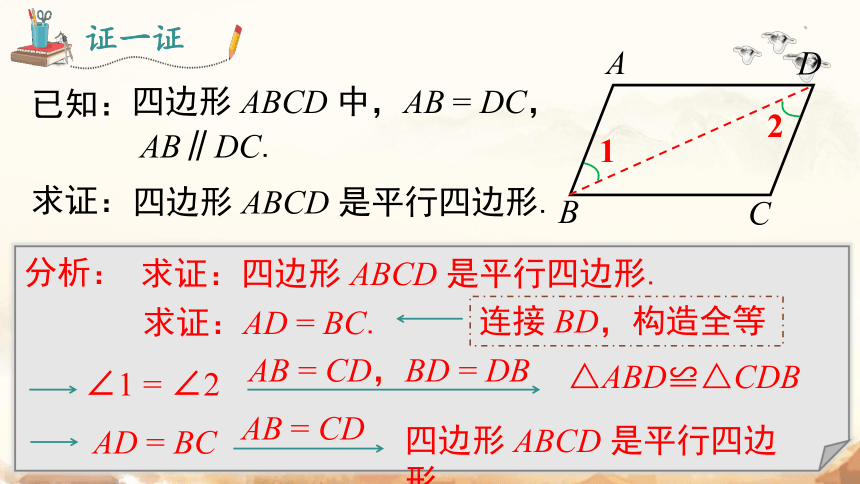
已知:
求证:
四边形 ABCD 中,AB = DC,
AB∥DC.
证一证
分析:
求证:四边形 ABCD 是平行四边形.
求证:AD = BC.
△ABD≌△CDB
∠1 = ∠2
AB = CD,BD = DB
连接 BD,构造全等
AD = BC
AB = CD
四边形 ABCD 是平行四边形
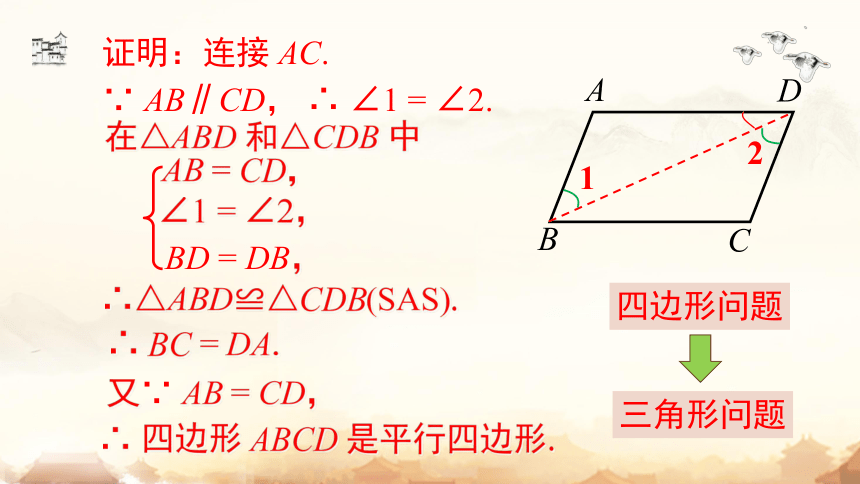
证明:连接 AC.
∵ AB∥CD, ∴ ∠1 = ∠2.
在△ABD 和△CDB 中
AB = CD,
BD = DB,
∠1 = ∠2,
∴△ABD≌△CDB(SAS).
∴ BC = DA.
又∵ AB = CD,
∴ 四边形 ABCD 是平行四边形.
B
D
A
C
2
1
四边形问题
三角形问题
归纳总结
平行四边形的判定定理
一组对边平行且相等的四边形是平行四边形.
几何语言描述:
∵在四边形 ABCD 中,
AB∥CD,AB = CD,
∴ 四边形 ABCD 是平行四边形.
B
D
A
C
典例精析
例1 如图 ,在平行四边形 ABCD 中,E,F 分别是 AB,CD 的中点.
求证:四边形 EBFD 是平行四边形.
A
B
C
D
E
F
分析:
平行四边形 ABCD
AB = CD,AB∥CD
E,F 分别是 AB,CD 的中点
EB = FD
四边形 EBFD 是平行四边形
证明:∵ 四边形 ABCD 是平行四边形,
∴ AB = CD,EB∥FD.
又∵ EB = AB ,FD = CD,
∴ EB = FD .
∴ 四边形 EBFD 是平行四边形.
例1 如图 ,在平行四边形 ABCD 中,E,F 分别是AB,CD 的中点. 求证:四边形 EBFD 是平行四边形.
A
B
C
D
E
F
1.已知四边形 ABCD 中有四个条件:AB∥CD,AB = CD,BC∥AD,BC = AD,从中任选两个,不能使四边形ABCD 成为平行四边形的选法是 ( )
A.AB∥CD,AB = CD
B.AB∥CD,BC∥AD
C.AB∥CD,BC = AD
D.AB = CD,BC = AD
C
练一练
2. 如图,点 A,B,C,D 在同一条直线上,点 E,F 分别在直线 AD 的两侧,AE = DF,∠A = ∠D,
AB = DC. 求证:四边形 BFCE 是平行四边形.
证明:∵ AB = CD,
∴ AB + BC = CD + BC,即 AC = BD.
在△ACE 和△DBF 中,
AC=BD ,∠A=∠D, AE=DF,
∴ △ACE≌△DBF(SAS).
∴ CE=BF,∠ACE=∠DBF.
∴ CE∥BF.
∴ 四边形 BFCE 是平行四边形.
边
角
对角线
对角线互相平分的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
现在你学会了几种平行四边形的判定方法
一组对边平行且相等的四边形是平行四边形
两组对边分别平行的四边形是平行四边形
归纳总结
例2 如图,△ABC 中,BD 平分∠ABC,DF∥BC,EF∥AC,试问 BF 与 CE 相等吗?为什么?
解:BF=CE.理由如下:
∵ DF∥BC,EF∥AC,
∴四边形 FECD 是平行四边形,
∠FDB = ∠DBE. ∴ FD = CE.
∵ BD 平分∠ABC,∴∠FBD = ∠EBD.
∴ ∠FBD = ∠FDB.
∴ BF = FD. ∴ BF=CE.
知识点2:平行四边形的性质与判定的综合运用
3. 四边形 ABCD 中,对角线 AC、BD 相交于点 O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD. 从中任选两个条件,能使四边形ABCD 为平行四边形的选法有( )
A.3 种 B.4 种
C.5 种 D.6 种
B
O
D
A
C
B
练一练
4. 如图,将 ABCD 沿过点 A 的直线 l 折叠,使点D 落到 AB 边上的点 D′ 处,折痕 l 交 CD 边于点 E,连接 BE.求证:四边形 BCED′ 是平行四边形.
证明:由题意得∠DAE = ∠D′AE,∠DEA = ∠D′EA,∠D = ∠AD′E,
∵ DE∥AD′,
∴ ∠DEA =∠EAD′,
∴ ∠DAE = ∠EAD′ = ∠DEA = ∠D′EA,
∴ ∠DAD′ = ∠DED′.
∴ 四边形 DAD′E 是平行四边形.
∴ DE = AD′.
∵ 四边形 ABCD 是平行四边形,
∴ AB∥DC,AB = DC,
∴ CE∥D′B,CE = D′B,
∴ 四边形 BCED′ 是平行四边形.
此题利用翻折变换的性质以及平行线的性质得出∠DAE =∠EAD′ =∠DEA =∠D′EA,再结合平行四边形的判定及性质进行解题.
总结
第肆章节
随堂练习
随堂练习
知识点1:对角线互相平分的四边形是平行四边形1.如图,在四边形ABCD中,对角线AC与BD相交于点O,OA=OC,要使四边形ABCD是平行四边形,可添加一个条件为 .
OB=OD(答案合理即可)
(第1题)
2. 如图,在平面直角坐标系中,A(-2,0),B(0,-3),C(2,0),要使四边形ABCD成为平行四边形,则点D的坐标为 .
(第2题)
(0,3)
(第3题)
3. 如图,若AO=OC,BD=6 cm,则OB= cm时,四边形ABCD是平行四边形.
3
知识点2:两组对角分别相等的四边形是平行四边形
4. 下列给出了四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的是( D ).
A. 1∶2∶3∶4 B. 2∶2∶3∶3
C. 2∶3∶3∶2 D. 2∶3∶2∶3
D
5. 如图,已知∠CBE=38°,要使四边形ABCD为平行四边形,则四边形ABCD的各内角度数依次为( D ).
A. 48°,132°, 48°,132°
B. 142°, 142°, 38°,38°
C. 38°, 38°, 142°,142°
D. 38°, 142°, 38°, 142°
(第5题)
D
6. 如图,延长△ABC的中线BD至点E,使DE=BD,连接AE,CE.
求证:四边形ABCE是平行四边形.
(第6题)
证明:∵BD是△ABC的AC边上的中线,
∴AD=CD.
∵DE=BD,∴四边形ABCD是平行四边形.
7. 如图,在四边形ABCD中,点E在BC的延长线上,∠B=∠D,∠A+∠DCE=180°.
求证:四边形ABCD是平行四边形.
(第7题)
证明:∵∠A+∠DCE=180°,∠BCD+∠DCE=180°,
∴∠A=∠BCD.
∵∠B=∠D,∴四边形ABCD是平行四边形.
8. 如图,在 ABCD中,M,N分别是AO,OC的中点,连接DN,BM.
(第8题)
求证:DN=BM.
证明:连接BN,DM.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵M,N分别是AO,OC的中点,
∴OM=AM,ON=NC. ∴OM=ON.
∴四边形MBND是平行四边形.∴DN=BM.
第伍章节
课堂小结
课堂小结
平行四边形的性质和判定有哪些?
边:
角:
对角线:
B
O
D
A
C
① AB∥CD, AD∥BC
② AB = CD, AD = BC
③ AB∥CD, AB = CD
∠BAD = ∠DCB,
∠ABC = ∠CDA
AO = CO,DO = BO
判定
性质
ABCD
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
人教版数学八年级下册
第十八章 平行四边形
汇报人:孙老师
汇报班级:X级X班
18.1.2 第2课时 平行四边形的判定(2)
18.1 平行四边形
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1. 平行四边形判定方法4:对角线 的四边形是平行四边形.
2. 平行四边形判定方法5:两组对角 的四边形是平行四边形.
互相平分
分别相等
第贰章节
新课导入
新课导入
求作:
∠A1B1C1 ,使∠A1B1C1
= ∠ABC.
1.已知:∠ABC,
A
B
C
3.作线段MN的垂直
平分线.
2.过点E作直线 l 的平行线.
l
E
M
N
第叁章节
新知探究
新知探究
知识点1: 一组对边平行且相等的四边形是平行四边形
探究:(可提出反例)
猜想一:一组对边相等的四边形是平行四边形.
等腰梯形
猜想不成立
探究:(可提出反例)
猜想二:一组对边平行的四边形是平行四边形.
猜想不成立
梯形
猜想三:一组对边平行且相等的四边形是平行四边形.
同学们,拿出一张白纸,在纸上画出一个平行四边形,然后写出已知和求证的条件,想一想怎么去证明?
B
D
A
C
B
D
A
C
2
1
四边形 ABCD 是平行四边形.
已知:
求证:
四边形 ABCD 中,AB = DC,
AB∥DC.
证一证
分析:
求证:四边形 ABCD 是平行四边形.
求证:AD = BC.
△ABD≌△CDB
∠1 = ∠2
AB = CD,BD = DB
连接 BD,构造全等
AD = BC
AB = CD
四边形 ABCD 是平行四边形
证明:连接 AC.
∵ AB∥CD, ∴ ∠1 = ∠2.
在△ABD 和△CDB 中
AB = CD,
BD = DB,
∠1 = ∠2,
∴△ABD≌△CDB(SAS).
∴ BC = DA.
又∵ AB = CD,
∴ 四边形 ABCD 是平行四边形.
B
D
A
C
2
1
四边形问题
三角形问题
归纳总结
平行四边形的判定定理
一组对边平行且相等的四边形是平行四边形.
几何语言描述:
∵在四边形 ABCD 中,
AB∥CD,AB = CD,
∴ 四边形 ABCD 是平行四边形.
B
D
A
C
典例精析
例1 如图 ,在平行四边形 ABCD 中,E,F 分别是 AB,CD 的中点.
求证:四边形 EBFD 是平行四边形.
A
B
C
D
E
F
分析:
平行四边形 ABCD
AB = CD,AB∥CD
E,F 分别是 AB,CD 的中点
EB = FD
四边形 EBFD 是平行四边形
证明:∵ 四边形 ABCD 是平行四边形,
∴ AB = CD,EB∥FD.
又∵ EB = AB ,FD = CD,
∴ EB = FD .
∴ 四边形 EBFD 是平行四边形.
例1 如图 ,在平行四边形 ABCD 中,E,F 分别是AB,CD 的中点. 求证:四边形 EBFD 是平行四边形.
A
B
C
D
E
F
1.已知四边形 ABCD 中有四个条件:AB∥CD,AB = CD,BC∥AD,BC = AD,从中任选两个,不能使四边形ABCD 成为平行四边形的选法是 ( )
A.AB∥CD,AB = CD
B.AB∥CD,BC∥AD
C.AB∥CD,BC = AD
D.AB = CD,BC = AD
C
练一练
2. 如图,点 A,B,C,D 在同一条直线上,点 E,F 分别在直线 AD 的两侧,AE = DF,∠A = ∠D,
AB = DC. 求证:四边形 BFCE 是平行四边形.
证明:∵ AB = CD,
∴ AB + BC = CD + BC,即 AC = BD.
在△ACE 和△DBF 中,
AC=BD ,∠A=∠D, AE=DF,
∴ △ACE≌△DBF(SAS).
∴ CE=BF,∠ACE=∠DBF.
∴ CE∥BF.
∴ 四边形 BFCE 是平行四边形.
边
角
对角线
对角线互相平分的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
现在你学会了几种平行四边形的判定方法
一组对边平行且相等的四边形是平行四边形
两组对边分别平行的四边形是平行四边形
归纳总结
例2 如图,△ABC 中,BD 平分∠ABC,DF∥BC,EF∥AC,试问 BF 与 CE 相等吗?为什么?
解:BF=CE.理由如下:
∵ DF∥BC,EF∥AC,
∴四边形 FECD 是平行四边形,
∠FDB = ∠DBE. ∴ FD = CE.
∵ BD 平分∠ABC,∴∠FBD = ∠EBD.
∴ ∠FBD = ∠FDB.
∴ BF = FD. ∴ BF=CE.
知识点2:平行四边形的性质与判定的综合运用
3. 四边形 ABCD 中,对角线 AC、BD 相交于点 O,给出下列四个条件:①AD∥BC;②AD=BC;③OA=OC;④OB=OD. 从中任选两个条件,能使四边形ABCD 为平行四边形的选法有( )
A.3 种 B.4 种
C.5 种 D.6 种
B
O
D
A
C
B
练一练
4. 如图,将 ABCD 沿过点 A 的直线 l 折叠,使点D 落到 AB 边上的点 D′ 处,折痕 l 交 CD 边于点 E,连接 BE.求证:四边形 BCED′ 是平行四边形.
证明:由题意得∠DAE = ∠D′AE,∠DEA = ∠D′EA,∠D = ∠AD′E,
∵ DE∥AD′,
∴ ∠DEA =∠EAD′,
∴ ∠DAE = ∠EAD′ = ∠DEA = ∠D′EA,
∴ ∠DAD′ = ∠DED′.
∴ 四边形 DAD′E 是平行四边形.
∴ DE = AD′.
∵ 四边形 ABCD 是平行四边形,
∴ AB∥DC,AB = DC,
∴ CE∥D′B,CE = D′B,
∴ 四边形 BCED′ 是平行四边形.
此题利用翻折变换的性质以及平行线的性质得出∠DAE =∠EAD′ =∠DEA =∠D′EA,再结合平行四边形的判定及性质进行解题.
总结
第肆章节
随堂练习
随堂练习
知识点1:对角线互相平分的四边形是平行四边形1.如图,在四边形ABCD中,对角线AC与BD相交于点O,OA=OC,要使四边形ABCD是平行四边形,可添加一个条件为 .
OB=OD(答案合理即可)
(第1题)
2. 如图,在平面直角坐标系中,A(-2,0),B(0,-3),C(2,0),要使四边形ABCD成为平行四边形,则点D的坐标为 .
(第2题)
(0,3)
(第3题)
3. 如图,若AO=OC,BD=6 cm,则OB= cm时,四边形ABCD是平行四边形.
3
知识点2:两组对角分别相等的四边形是平行四边形
4. 下列给出了四边形ABCD中∠A,∠B,∠C,∠D的度数之比,其中能判定四边形ABCD是平行四边形的是( D ).
A. 1∶2∶3∶4 B. 2∶2∶3∶3
C. 2∶3∶3∶2 D. 2∶3∶2∶3
D
5. 如图,已知∠CBE=38°,要使四边形ABCD为平行四边形,则四边形ABCD的各内角度数依次为( D ).
A. 48°,132°, 48°,132°
B. 142°, 142°, 38°,38°
C. 38°, 38°, 142°,142°
D. 38°, 142°, 38°, 142°
(第5题)
D
6. 如图,延长△ABC的中线BD至点E,使DE=BD,连接AE,CE.
求证:四边形ABCE是平行四边形.
(第6题)
证明:∵BD是△ABC的AC边上的中线,
∴AD=CD.
∵DE=BD,∴四边形ABCD是平行四边形.
7. 如图,在四边形ABCD中,点E在BC的延长线上,∠B=∠D,∠A+∠DCE=180°.
求证:四边形ABCD是平行四边形.
(第7题)
证明:∵∠A+∠DCE=180°,∠BCD+∠DCE=180°,
∴∠A=∠BCD.
∵∠B=∠D,∴四边形ABCD是平行四边形.
8. 如图,在 ABCD中,M,N分别是AO,OC的中点,连接DN,BM.
(第8题)
求证:DN=BM.
证明:连接BN,DM.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵M,N分别是AO,OC的中点,
∴OM=AM,ON=NC. ∴OM=ON.
∴四边形MBND是平行四边形.∴DN=BM.
第伍章节
课堂小结
课堂小结
平行四边形的性质和判定有哪些?
边:
角:
对角线:
B
O
D
A
C
① AB∥CD, AD∥BC
② AB = CD, AD = BC
③ AB∥CD, AB = CD
∠BAD = ∠DCB,
∠ABC = ∠CDA
AO = CO,DO = BO
判定
性质
ABCD
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
