19.1.1常量与变量第1课时 课件(共30张PPT)
文档属性
| 名称 | 19.1.1常量与变量第1课时 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 00:00:00 | ||
图片预览











文档简介
(共30张PPT)
人教版数学八年级下册
第19章 一次函数
汇报人:孙老师
汇报班级:X级X班
19.1.1 第1课时 常量与变量
19.1 函数
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.探索数量关系和变化规律.
2.了解变量、常量的意义,能正确区分变量和常量.
第贰章节
新课导入
新课导入
在这个过程中,哪些量变化了?哪些量没变?
汽车以 60 km/h 的速度匀速行驶,行驶路程为 s km,行驶时间为 t h.
这些量有什么关系呢?
第叁章节
新知探究
新知探究
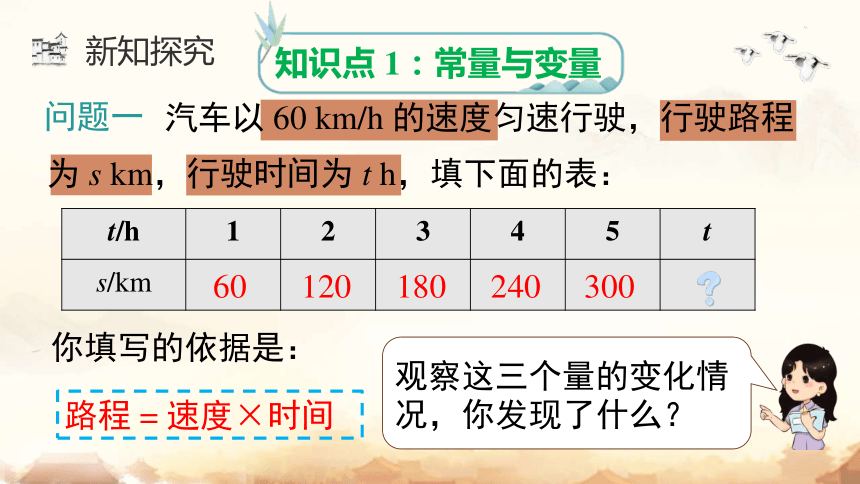
你填写的依据是:
问题一
知识点 1:常量与变量
t/h 1 2 3 4 5 t
s/km
60
120
180
240
300
路程 = 速度×时间
观察这三个量的变化情况,你发现了什么?
汽车以 60 km/h 的速度匀速行驶,行驶路程为 s km,行驶时间为 t h,填下面的表:
1.在以上这个过程中,变化的量是_______
_________.不变化的量是 .
2.试用含 t 的式子表示 s. s =_______.
时间 t、
速度 60 km/h
60 t
路程 s
s
t
填一填
这个过程反映出路程___随时间___的变化过程.
不变的量
变化的量
变化的量
汽车以 60 km/h 的速度匀速行驶,行驶路程为 s km,
行驶时间为 t h.
问题二
第一场票房收入 =
第二场票房收入 =
第三场票房收入 =
你列式的依据是:
10×205 = 2050(元)
10×150 = 1500(元)
10×310 = 3100(元)
售出 x 张的票房收入 =
票房收入 = 售价×售票张数
电影票的售价为 10 元/张 ,第一场售出150 张,第二场售出 205 张,第三场售出 310 张,三场电影票的票房收入各多少元?设一场电影售出票 x 张,票房收入为 y 元,每场的票房收入是多少呢 ?
10x
1.在以上这个过程中,变化的量是________________________.不变化的量是_________.
2.试用含 x 的式子表示 y,y =_________
售票张数 x、票房收入 y
售价 10 元
y
x
填一填
这个过程反映出收入___随数量___的变化过程.
变化的量
如图所示,圆形水波慢慢地扩大,在这一过程中,当圆的半径 r 分别为 10 cm,20 cm,30 cm 时,圆的面积 S 分别为多少?怎样用半径 r 来表示面积 S
问题三
当半径为 10 cm 时,圆的面积为 100π cm2
当半径为 20 cm 时,圆的面积为 400π cm2
......
这个过程反映出______随______的变化过程.
S = πr2
π 是不变的量
面积 S
半径 r
问题四
用 10 m 长的绳子围一个矩形.当矩形的一边长 x 分别为 3 m,3.5 m,4 m,4.5 m 时,它的邻边长 y 分别为多少
y 的值随 x 的值的变化而变化吗
当一边长为 3 m 时,邻边长为 2 m.
当一边长为 3.5 m 时,邻边长为 1.5 m.
......
y = 5 - x
这个过程反映出_________随________的变化过程.
边长 x
邻边长 y
总结归纳
上面这些问题中涉及到的量,你会怎样分类呢
S = 60t
y = 10x
S = πr2
常量与变量
在一个变化过程中,我们称数值发生变化的量为变量,数值始终不变的量为常量.
不变的量
变化的量
例如:汽车行驶的速度
汽车行驶的路程
汽车行驶的时间
y = 5 - x
例1 指出下列事件过程中的常量与变量
(1)某水果店橘子的单价为 5 元/千克,买 a 千橘子的总价为 m 元,其中常量是 ,变量是 ;
(2)周长 C 与圆的半径 r 之间的关系式是 C=2πr,其中常量是 ,变量是 ;
(3)三角形的一边长 5 cm,它的面积 S (cm2) 与这边上的高 h (cm) 的关系式 中,其中常量是 ,变量是 ;
5
a,m
2,π
C, r
注意:π 是一个确定的数,是常量
S, h
典例精析
_____
1. 指出下列事件过程中的变量和常量:
(1) 汽油的价格是 7.4 元/升,加油 x 升,车主加油付油费为 y 元;
(2) 小明看一本 200 页的小说,看完这本小说需要t 天,平均每天所看的页数为 n;
练一练
常量
变量
(3) 用长为 40 cm 的绳子围矩形,围成的矩形一边长为 x cm,其面积为 S cm2.
(4) 若直角三角形中的一个锐角的度数为 α,则另一个锐角 β (度)与 α 间的关系式是 β = 90-α.
常量
变量
合作交流
你知道如何判断常量和变量吗?
判断常量和变量的方法:
(1) 看它是否在同一个变化过程中;
(2) 看它在这个变化过程中的取值是否改变.
指出一个变化过程中的常量时,应连同它前面的符号.
总结
例2 一名老师带领 x 名学生到动物园参观,已知成人票每张 30 元,学生票每张 10 元,设门票的总费用为 y 元,则 y 与 x 之间的关系式为_____________.
知识点 2:确定两个变量之间的关系式
y = 10x + 30
等量关系:
门票总费用:一个成人费用 + x 个学生费用
=1×成人票价 + x×学生票价
则用含重物质量 m (kg) 的式子表示受力后的弹簧长度 L(cm) 为 .
2. 如果弹簧原长为 12 cm,每 1 kg 重物使弹簧压缩 0.5 cm,
L = 12 - 0.5m
练一练
第肆章节
随堂练习
随堂练习
若球的体积为V,半径为R,则 .
其中_________是变量,________是常量.
(1)常量、变量与字母的指数没有关系.
(2)π 是常量,不是变量.
V,R
2. 已知路程 s,速度 v 和时间 t 的关系式为 s=vt,则下列
说法中正确的是( ).
当 s 一定时,v 是常量,t 是变量
当 v 一定时,t 是常量,s 是变量
当 t 一定时,t 是常量,v 是变量
当 t 一定时,s 是常量,v 是变量
C
s 是常量,v,t 是变量
v 是常量,s,t 是变量
t 是常量,s,v 是变量
√
判断一个量是不是变量,关键是看其数值是否发生变化.
常量与变量是相对的,前提是“在一个变化过程中”.
3. 回顾多边形的相关知识,随着多边形边数 n 的增加,多边形的内角和 α 和外角和 β 会有什么变化?请用式子表示出它们的关系.
解:α 的值随 n 的值的变化而变化,边数 n 每增加1,内角和 α 增加180°,α =(n-2)·180°;
β 不受 n 的影响,β =360°.
4. 如图,在矩形 ABCD 中,点 M 在边 BC 上,点 N 在
边 CD 上. 设 BM=a,CN=b,则△BMN 的面积 .
(1)若保持点 M 不动,点 N 在 CD 上运动,
请指出 中的变量与常量;
(2)若保持点 N 不动,点 M 在 BC 上运动,
请指出 中的变量与常量.
几何画板示意图
解:(1)S 和 b 是变量, 和 a 是常量;
(2)S 和 a 是变量, 和 b 是常量.
2
1
2
1
5. 已知某易拉罐厂设计一种易拉罐,在设计过程中发现符合要求的易拉罐的底面半径与用铝量有如表关系:
(1)上表反映了哪两个变量之间的关系?
(2)当易拉罐底面半径为 2.4 cm 时,易拉罐需要的用铝量
是多少?
(3)根据表格中的数据,你认为易拉罐的底面半径为多少
时比较适宜?说说你的理由.
底面半径 x/cm 1.6 2.0 2.4 2.8 3.2 3.6 4.0
用铝量 y/cm3 6.9 6.0 5.6 5.5 5.7 6.0 6.5
底面半径 x/cm 1.6 2.0 2.4 2.8 3.2 3.6 4.0
用铝量 y/cm3 6.9 6.0 5.6 5.5 5.7 6.0 6.5
解:(1)反映了用铝量 y 与底面半径 x 之间的关系.
(2)当底面半径为 2.4 cm时,易拉罐需要的用铝量是
5.6 cm3.
(3)易拉罐的底面半径为 2.8 cm时比较适宜,理由如下:
当易拉罐的底面半径为 2.8 cm 时,用铝量最少,
成本最低.
第伍章节
课堂小结
课堂小结
在一个变化过程中
数值始终不变的量为常量
数值发生变化的量为变量
单值对应关系:当一个变量取定一个值时,另一变量有且只有一个对应值.
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
人教版数学八年级下册
第19章 一次函数
汇报人:孙老师
汇报班级:X级X班
19.1.1 第1课时 常量与变量
19.1 函数
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.探索数量关系和变化规律.
2.了解变量、常量的意义,能正确区分变量和常量.
第贰章节
新课导入
新课导入
在这个过程中,哪些量变化了?哪些量没变?
汽车以 60 km/h 的速度匀速行驶,行驶路程为 s km,行驶时间为 t h.
这些量有什么关系呢?
第叁章节
新知探究
新知探究
你填写的依据是:
问题一
知识点 1:常量与变量
t/h 1 2 3 4 5 t
s/km
60
120
180
240
300
路程 = 速度×时间
观察这三个量的变化情况,你发现了什么?
汽车以 60 km/h 的速度匀速行驶,行驶路程为 s km,行驶时间为 t h,填下面的表:
1.在以上这个过程中,变化的量是_______
_________.不变化的量是 .
2.试用含 t 的式子表示 s. s =_______.
时间 t、
速度 60 km/h
60 t
路程 s
s
t
填一填
这个过程反映出路程___随时间___的变化过程.
不变的量
变化的量
变化的量
汽车以 60 km/h 的速度匀速行驶,行驶路程为 s km,
行驶时间为 t h.
问题二
第一场票房收入 =
第二场票房收入 =
第三场票房收入 =
你列式的依据是:
10×205 = 2050(元)
10×150 = 1500(元)
10×310 = 3100(元)
售出 x 张的票房收入 =
票房收入 = 售价×售票张数
电影票的售价为 10 元/张 ,第一场售出150 张,第二场售出 205 张,第三场售出 310 张,三场电影票的票房收入各多少元?设一场电影售出票 x 张,票房收入为 y 元,每场的票房收入是多少呢 ?
10x
1.在以上这个过程中,变化的量是________________________.不变化的量是_________.
2.试用含 x 的式子表示 y,y =_________
售票张数 x、票房收入 y
售价 10 元
y
x
填一填
这个过程反映出收入___随数量___的变化过程.
变化的量
如图所示,圆形水波慢慢地扩大,在这一过程中,当圆的半径 r 分别为 10 cm,20 cm,30 cm 时,圆的面积 S 分别为多少?怎样用半径 r 来表示面积 S
问题三
当半径为 10 cm 时,圆的面积为 100π cm2
当半径为 20 cm 时,圆的面积为 400π cm2
......
这个过程反映出______随______的变化过程.
S = πr2
π 是不变的量
面积 S
半径 r
问题四
用 10 m 长的绳子围一个矩形.当矩形的一边长 x 分别为 3 m,3.5 m,4 m,4.5 m 时,它的邻边长 y 分别为多少
y 的值随 x 的值的变化而变化吗
当一边长为 3 m 时,邻边长为 2 m.
当一边长为 3.5 m 时,邻边长为 1.5 m.
......
y = 5 - x
这个过程反映出_________随________的变化过程.
边长 x
邻边长 y
总结归纳
上面这些问题中涉及到的量,你会怎样分类呢
S = 60t
y = 10x
S = πr2
常量与变量
在一个变化过程中,我们称数值发生变化的量为变量,数值始终不变的量为常量.
不变的量
变化的量
例如:汽车行驶的速度
汽车行驶的路程
汽车行驶的时间
y = 5 - x
例1 指出下列事件过程中的常量与变量
(1)某水果店橘子的单价为 5 元/千克,买 a 千橘子的总价为 m 元,其中常量是 ,变量是 ;
(2)周长 C 与圆的半径 r 之间的关系式是 C=2πr,其中常量是 ,变量是 ;
(3)三角形的一边长 5 cm,它的面积 S (cm2) 与这边上的高 h (cm) 的关系式 中,其中常量是 ,变量是 ;
5
a,m
2,π
C, r
注意:π 是一个确定的数,是常量
S, h
典例精析
_____
1. 指出下列事件过程中的变量和常量:
(1) 汽油的价格是 7.4 元/升,加油 x 升,车主加油付油费为 y 元;
(2) 小明看一本 200 页的小说,看完这本小说需要t 天,平均每天所看的页数为 n;
练一练
常量
变量
(3) 用长为 40 cm 的绳子围矩形,围成的矩形一边长为 x cm,其面积为 S cm2.
(4) 若直角三角形中的一个锐角的度数为 α,则另一个锐角 β (度)与 α 间的关系式是 β = 90-α.
常量
变量
合作交流
你知道如何判断常量和变量吗?
判断常量和变量的方法:
(1) 看它是否在同一个变化过程中;
(2) 看它在这个变化过程中的取值是否改变.
指出一个变化过程中的常量时,应连同它前面的符号.
总结
例2 一名老师带领 x 名学生到动物园参观,已知成人票每张 30 元,学生票每张 10 元,设门票的总费用为 y 元,则 y 与 x 之间的关系式为_____________.
知识点 2:确定两个变量之间的关系式
y = 10x + 30
等量关系:
门票总费用:一个成人费用 + x 个学生费用
=1×成人票价 + x×学生票价
则用含重物质量 m (kg) 的式子表示受力后的弹簧长度 L(cm) 为 .
2. 如果弹簧原长为 12 cm,每 1 kg 重物使弹簧压缩 0.5 cm,
L = 12 - 0.5m
练一练
第肆章节
随堂练习
随堂练习
若球的体积为V,半径为R,则 .
其中_________是变量,________是常量.
(1)常量、变量与字母的指数没有关系.
(2)π 是常量,不是变量.
V,R
2. 已知路程 s,速度 v 和时间 t 的关系式为 s=vt,则下列
说法中正确的是( ).
当 s 一定时,v 是常量,t 是变量
当 v 一定时,t 是常量,s 是变量
当 t 一定时,t 是常量,v 是变量
当 t 一定时,s 是常量,v 是变量
C
s 是常量,v,t 是变量
v 是常量,s,t 是变量
t 是常量,s,v 是变量
√
判断一个量是不是变量,关键是看其数值是否发生变化.
常量与变量是相对的,前提是“在一个变化过程中”.
3. 回顾多边形的相关知识,随着多边形边数 n 的增加,多边形的内角和 α 和外角和 β 会有什么变化?请用式子表示出它们的关系.
解:α 的值随 n 的值的变化而变化,边数 n 每增加1,内角和 α 增加180°,α =(n-2)·180°;
β 不受 n 的影响,β =360°.
4. 如图,在矩形 ABCD 中,点 M 在边 BC 上,点 N 在
边 CD 上. 设 BM=a,CN=b,则△BMN 的面积 .
(1)若保持点 M 不动,点 N 在 CD 上运动,
请指出 中的变量与常量;
(2)若保持点 N 不动,点 M 在 BC 上运动,
请指出 中的变量与常量.
几何画板示意图
解:(1)S 和 b 是变量, 和 a 是常量;
(2)S 和 a 是变量, 和 b 是常量.
2
1
2
1
5. 已知某易拉罐厂设计一种易拉罐,在设计过程中发现符合要求的易拉罐的底面半径与用铝量有如表关系:
(1)上表反映了哪两个变量之间的关系?
(2)当易拉罐底面半径为 2.4 cm 时,易拉罐需要的用铝量
是多少?
(3)根据表格中的数据,你认为易拉罐的底面半径为多少
时比较适宜?说说你的理由.
底面半径 x/cm 1.6 2.0 2.4 2.8 3.2 3.6 4.0
用铝量 y/cm3 6.9 6.0 5.6 5.5 5.7 6.0 6.5
底面半径 x/cm 1.6 2.0 2.4 2.8 3.2 3.6 4.0
用铝量 y/cm3 6.9 6.0 5.6 5.5 5.7 6.0 6.5
解:(1)反映了用铝量 y 与底面半径 x 之间的关系.
(2)当底面半径为 2.4 cm时,易拉罐需要的用铝量是
5.6 cm3.
(3)易拉罐的底面半径为 2.8 cm时比较适宜,理由如下:
当易拉罐的底面半径为 2.8 cm 时,用铝量最少,
成本最低.
第伍章节
课堂小结
课堂小结
在一个变化过程中
数值始终不变的量为常量
数值发生变化的量为变量
单值对应关系:当一个变量取定一个值时,另一变量有且只有一个对应值.
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
