19.1.1函数第2课时 课件(共32张PPT)
文档属性
| 名称 | 19.1.1函数第2课时 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 14:12:30 | ||
图片预览











文档简介
(共32张PPT)
人教版数学八年级下册
第19章 一次函数
汇报人:孙老师
汇报班级:X级X班
19.1.1 第2课时 函数
19.1 函数
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1. 函数的表示方法: 、 、 .
2. 函数的图象是由一系列的点组成的图形.描点法画函数图象的一般步骤是: 、 、 .
解析式法
列表法
图象法
列表
描点
连线
第贰章节
新课导入
新课导入
汽车耗油量为 0.1 L/km,油箱中有汽油 50 L. 如果在行驶过程中不再加油,那么下列各量中:
①汽车耗油量;②行驶路程x;
③汽车油箱中的剩余油量y.
变量是___________,常量是__________.
②③
①
在一个变化过程中,数值发生变化的量为变量,数值始终不变的量为常量.
上面几个变量之间有什么联系吗?
汽车耗油量为 0.1 L/km,油箱中有汽油 50 L. 如果在行驶过程中不再加油,那么下列各量中:
①汽车耗油量;②行驶路程x;
③汽车油箱中的剩余油量y.
变量是___________,常量是__________.
②③
①
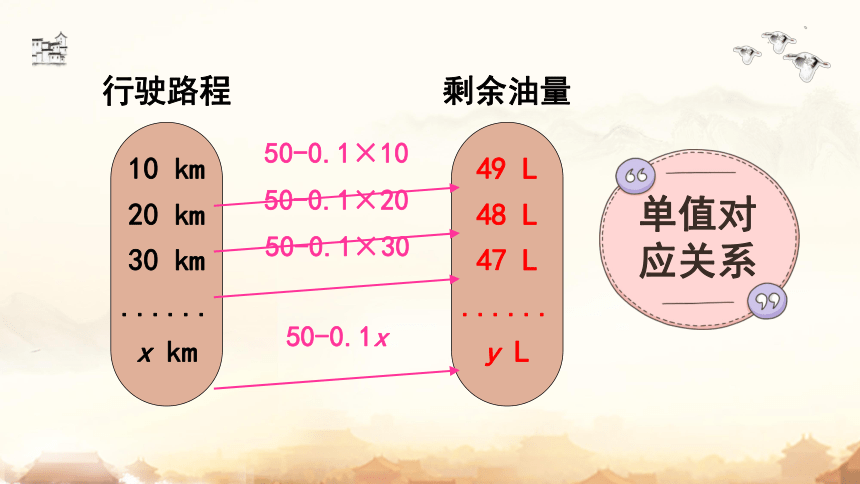
行驶路程 x
剩余油量 y
10 km
x km
20 km
30 km
......
49 L
y L
48 L
47 L
......
50-0.1×10
50-0.1×20
50-0.1×30
50-0.1x
单值对应关系
第叁章节
新知探究
新知探究
知识点 1:函数的相关概念
问题一 汽车以 60 km/h 的速度匀速行驶,行驶路程为 s km,行驶时间为 t h,填下面的表:
t/h 1 2 3 4 5 t
s/km
60
120
180
240
300
60t
这个问题中有几个变量?
两个
___________随着 ___ 的变化而变化,
当 确定一个值时, 就随之确定一个值.
行驶路程 s
行驶时间 t
行驶时间 t
行驶路程 s
问题二 电影票的售价为 10 元/张 ,第一场售出150 张,第二场售出 205 张,第三场售出 310 张,三场电影票的票房收入各多少元?设一场电影售出票 x 张,票房收入为 y 元,每场的票房收入是多少呢 ?
这个问题中有几个变量
两个
当 x 取定一个值时,y 有几个值与之对应
一个
y = 10x
问题三 在圆的面积 S 和半径 r 中,r 每取一个值,S 都有唯一值与它对应吗
S = πr2
根据圆的面积计算公式 S = πr2,由于 π 为常量,所以 r 每取一个值,S 都有唯一值与它对应.
同理 问题四 中边长 x 每取一个值,邻边长 y 都有唯一值与它对应.
思考:上面的三个问题中,各变量之间有什么共同特点?
① 行驶路程 s 、行驶时间 t;
② 票房收入 y、售出票 x;
③ 圆的面积 S 、半径 r.
④ 矩形的边长 x 、邻边长 y.
上面的每个问题中的两个变量互相联系,当其中一个变量取定一个值时,另一个变量就有唯一确定的值与其对应.
总结
函数的概念
一般地,在某个变化过程中,如果有两个变量 x 与 y,并且对于 x 的每一个确定的值,y 都有唯一确定的值与它对应,那么我们就说 x 是自变量,y 是 x 的函数.
如果当 x = a 时 y = b,那么 b 叫做当自变量的值为 a 时的函数值.
下图是体检时的心电图,图上点的横坐标 x 表示时间,纵坐标 y 表示心脏部位的生物电流,它们是两个变量.在心电图中,对于 x 的每一个确定的值,y 都有唯一确定的值与其对应吗?
说一说
自变量
y 是 x 的函数
例1 下列关于变量 x ,y 的关系式:① y = 2x + 3; ② y = x2 + 3;③ y = 2| x |;④ y2 - 3x = 10,其中表示 y 是 x 的函数关系的是 .
①②③
典例精析
解析:① 当 x = 1 时, y = 5;当 x = 2 时, y = 7 ......
对于 x 的每一个确定的值,y 都有唯一确定的值与它对应,则 y 是 x 的函数;同理 ② ③.
④ 当 x = 1 时, y2 = 13,y = . 对于 x 的每一个确定的值,y 不唯一,则 y 不是 x 的函数.
1. 填表并回答问题:
(1) 对于 x 的每一个值,y 都有唯一的值与之对应吗?答: .
(2) y 是 x 的函数吗?为什么?
x 1 4 9 16
y = ±2x
2 和-2
8 和-8
18 和-18
32 和-32
不是
答:不是,因为 y 的值不是唯一的.
关键词:两个变量,给一个 x,得一个 y.
易错点:
顺序不要反.
练一练
(1) 求当 x = 2 ,3,-3 时,函数的值;
(2) 求当 x 取什么值时,函数的值为 0.
把自变量 x 的值带入关系式中,即可求出函数的值.
例2 已知函数
解:(1) 当 x = 2 时,y = ;
当 x = 3 时,y = ;
当 x = -3 时,y = 7.
(2) 令 解得 x =
即当 x = 时,y = 0.
问题:请用含自变量的式子表示下列问题中的函数关系:
问题 (1) 中,t 取 -2 有实际意义吗?
问题 (2) 中,n 取 2 有意义吗?
知识点 2:确定自变量的取值范围
(1) 汽车以 60 km/h 的速度匀速行驶,行驶的时间为 t (单位:h),行驶的路程为 s (单位:km);
(2) 多边形的边数为 n,内角和的度数为 y.
在实际问题中,函数的自变量取值范围往往是有限制的,在限制的范围内,函数才有实际意义;超出这个范围,函数没有实际意义,我们把这种自变量可以取的数值范围叫函数的自变量取值范围.
根据刚才问题的思考,你认为函数的自变量可以取任意值吗?
例3 汽车的油箱中有汽油 50 L,如果不再加油,那么油箱中的油量 y(单位:L)随行驶里程 x(单位:km)的增加而减少,平均耗油量为 0.1 L/km.
(1)写出表示 y 与 x 的函数关系的式子.
解:(1) 函数关系式为: y = 50-0.1x
油箱中的剩油量、汽车耗油量与油箱中原有油量之间有怎样的数量关系?
叫做函数的解析式
0.1x 表示的意义是什么?
(2) 由 x≥0 及 50-0.1x≥0
得 0≤x≤500
∴自变量的取值范围是
0≤x≤500
汽车行驶里程,油箱中的油量均不能为负数!
确定自变量的取值范围时,不仅要考虑使函数解析式有意义,而且还要注意各变量所代表的实际意义.
总结
(2) 指出自变量 x 的取值范围;
(3) 汽车行驶 200 km 时,油箱中还有多少油?
(3) 当 x = 200 时,函数 y 的值为
y = 50-0.1×200 = 30.
因此,当汽车行驶 200 km 时,油箱中还有油 30 L.
第肆章节
随堂练习
随堂练习
知识点1:根据解析式画函数图象
1. 下列各点在函数y=3x-1的图象上的是( B ).
A. (0,1) B. (2,5)
C. (-3,7) D. (1,1)
2. 若点(1,6)在函数y=kx+2k-3的图象上,则k的值为 .
B
3
3. 完成表格并画出函数y=-2x+1 的图象.
(第3题)
(第3题)
x … -3 -1 0 1 2 …
y=-2x+1 … 7 3 1 -1 -3 …
-1
1
7
1
-3
知识点2:根据函数图象解决实际问题
4. 看图填空.
(第4题)
(1)小明去图书馆行驶了 km,用了 min.
(2)他在图书馆停留了 min.
4
30
70
(3)小明从图书馆返回家中的速度是每小时 km.
(4)小明从图书馆返回家中用了 min.
12
20
5. 函数y= 中,自变量x的取值范围是 .
6. 已知点P(a-1,5)在函数y=3x-4的图象上,则a的值为 .
7. 小明的爷爷吃过晚饭后,出门散步,在报亭看了一会儿报纸才回家.小明绘制了爷爷离家的路程s与外出的时间t之间的关系图,如图所示.
x≠3
4
(第7题)
(1)报亭离爷爷家 m.
(2)爷爷在报亭看报纸用了 min.
(3)爷爷走去报亭的平均速度是 m/min.
400
15
40
第伍章节
课堂小结
课堂小结
变量和常量
自变量、自变量的函数
函数值
自变量的取值范围
解析式
函数
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
人教版数学八年级下册
第19章 一次函数
汇报人:孙老师
汇报班级:X级X班
19.1.1 第2课时 函数
19.1 函数
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1. 函数的表示方法: 、 、 .
2. 函数的图象是由一系列的点组成的图形.描点法画函数图象的一般步骤是: 、 、 .
解析式法
列表法
图象法
列表
描点
连线
第贰章节
新课导入
新课导入
汽车耗油量为 0.1 L/km,油箱中有汽油 50 L. 如果在行驶过程中不再加油,那么下列各量中:
①汽车耗油量;②行驶路程x;
③汽车油箱中的剩余油量y.
变量是___________,常量是__________.
②③
①
在一个变化过程中,数值发生变化的量为变量,数值始终不变的量为常量.
上面几个变量之间有什么联系吗?
汽车耗油量为 0.1 L/km,油箱中有汽油 50 L. 如果在行驶过程中不再加油,那么下列各量中:
①汽车耗油量;②行驶路程x;
③汽车油箱中的剩余油量y.
变量是___________,常量是__________.
②③
①
行驶路程 x
剩余油量 y
10 km
x km
20 km
30 km
......
49 L
y L
48 L
47 L
......
50-0.1×10
50-0.1×20
50-0.1×30
50-0.1x
单值对应关系
第叁章节
新知探究
新知探究
知识点 1:函数的相关概念
问题一 汽车以 60 km/h 的速度匀速行驶,行驶路程为 s km,行驶时间为 t h,填下面的表:
t/h 1 2 3 4 5 t
s/km
60
120
180
240
300
60t
这个问题中有几个变量?
两个
___________随着 ___ 的变化而变化,
当 确定一个值时, 就随之确定一个值.
行驶路程 s
行驶时间 t
行驶时间 t
行驶路程 s
问题二 电影票的售价为 10 元/张 ,第一场售出150 张,第二场售出 205 张,第三场售出 310 张,三场电影票的票房收入各多少元?设一场电影售出票 x 张,票房收入为 y 元,每场的票房收入是多少呢 ?
这个问题中有几个变量
两个
当 x 取定一个值时,y 有几个值与之对应
一个
y = 10x
问题三 在圆的面积 S 和半径 r 中,r 每取一个值,S 都有唯一值与它对应吗
S = πr2
根据圆的面积计算公式 S = πr2,由于 π 为常量,所以 r 每取一个值,S 都有唯一值与它对应.
同理 问题四 中边长 x 每取一个值,邻边长 y 都有唯一值与它对应.
思考:上面的三个问题中,各变量之间有什么共同特点?
① 行驶路程 s 、行驶时间 t;
② 票房收入 y、售出票 x;
③ 圆的面积 S 、半径 r.
④ 矩形的边长 x 、邻边长 y.
上面的每个问题中的两个变量互相联系,当其中一个变量取定一个值时,另一个变量就有唯一确定的值与其对应.
总结
函数的概念
一般地,在某个变化过程中,如果有两个变量 x 与 y,并且对于 x 的每一个确定的值,y 都有唯一确定的值与它对应,那么我们就说 x 是自变量,y 是 x 的函数.
如果当 x = a 时 y = b,那么 b 叫做当自变量的值为 a 时的函数值.
下图是体检时的心电图,图上点的横坐标 x 表示时间,纵坐标 y 表示心脏部位的生物电流,它们是两个变量.在心电图中,对于 x 的每一个确定的值,y 都有唯一确定的值与其对应吗?
说一说
自变量
y 是 x 的函数
例1 下列关于变量 x ,y 的关系式:① y = 2x + 3; ② y = x2 + 3;③ y = 2| x |;④ y2 - 3x = 10,其中表示 y 是 x 的函数关系的是 .
①②③
典例精析
解析:① 当 x = 1 时, y = 5;当 x = 2 时, y = 7 ......
对于 x 的每一个确定的值,y 都有唯一确定的值与它对应,则 y 是 x 的函数;同理 ② ③.
④ 当 x = 1 时, y2 = 13,y = . 对于 x 的每一个确定的值,y 不唯一,则 y 不是 x 的函数.
1. 填表并回答问题:
(1) 对于 x 的每一个值,y 都有唯一的值与之对应吗?答: .
(2) y 是 x 的函数吗?为什么?
x 1 4 9 16
y = ±2x
2 和-2
8 和-8
18 和-18
32 和-32
不是
答:不是,因为 y 的值不是唯一的.
关键词:两个变量,给一个 x,得一个 y.
易错点:
顺序不要反.
练一练
(1) 求当 x = 2 ,3,-3 时,函数的值;
(2) 求当 x 取什么值时,函数的值为 0.
把自变量 x 的值带入关系式中,即可求出函数的值.
例2 已知函数
解:(1) 当 x = 2 时,y = ;
当 x = 3 时,y = ;
当 x = -3 时,y = 7.
(2) 令 解得 x =
即当 x = 时,y = 0.
问题:请用含自变量的式子表示下列问题中的函数关系:
问题 (1) 中,t 取 -2 有实际意义吗?
问题 (2) 中,n 取 2 有意义吗?
知识点 2:确定自变量的取值范围
(1) 汽车以 60 km/h 的速度匀速行驶,行驶的时间为 t (单位:h),行驶的路程为 s (单位:km);
(2) 多边形的边数为 n,内角和的度数为 y.
在实际问题中,函数的自变量取值范围往往是有限制的,在限制的范围内,函数才有实际意义;超出这个范围,函数没有实际意义,我们把这种自变量可以取的数值范围叫函数的自变量取值范围.
根据刚才问题的思考,你认为函数的自变量可以取任意值吗?
例3 汽车的油箱中有汽油 50 L,如果不再加油,那么油箱中的油量 y(单位:L)随行驶里程 x(单位:km)的增加而减少,平均耗油量为 0.1 L/km.
(1)写出表示 y 与 x 的函数关系的式子.
解:(1) 函数关系式为: y = 50-0.1x
油箱中的剩油量、汽车耗油量与油箱中原有油量之间有怎样的数量关系?
叫做函数的解析式
0.1x 表示的意义是什么?
(2) 由 x≥0 及 50-0.1x≥0
得 0≤x≤500
∴自变量的取值范围是
0≤x≤500
汽车行驶里程,油箱中的油量均不能为负数!
确定自变量的取值范围时,不仅要考虑使函数解析式有意义,而且还要注意各变量所代表的实际意义.
总结
(2) 指出自变量 x 的取值范围;
(3) 汽车行驶 200 km 时,油箱中还有多少油?
(3) 当 x = 200 时,函数 y 的值为
y = 50-0.1×200 = 30.
因此,当汽车行驶 200 km 时,油箱中还有油 30 L.
第肆章节
随堂练习
随堂练习
知识点1:根据解析式画函数图象
1. 下列各点在函数y=3x-1的图象上的是( B ).
A. (0,1) B. (2,5)
C. (-3,7) D. (1,1)
2. 若点(1,6)在函数y=kx+2k-3的图象上,则k的值为 .
B
3
3. 完成表格并画出函数y=-2x+1 的图象.
(第3题)
(第3题)
x … -3 -1 0 1 2 …
y=-2x+1 … 7 3 1 -1 -3 …
-1
1
7
1
-3
知识点2:根据函数图象解决实际问题
4. 看图填空.
(第4题)
(1)小明去图书馆行驶了 km,用了 min.
(2)他在图书馆停留了 min.
4
30
70
(3)小明从图书馆返回家中的速度是每小时 km.
(4)小明从图书馆返回家中用了 min.
12
20
5. 函数y= 中,自变量x的取值范围是 .
6. 已知点P(a-1,5)在函数y=3x-4的图象上,则a的值为 .
7. 小明的爷爷吃过晚饭后,出门散步,在报亭看了一会儿报纸才回家.小明绘制了爷爷离家的路程s与外出的时间t之间的关系图,如图所示.
x≠3
4
(第7题)
(1)报亭离爷爷家 m.
(2)爷爷在报亭看报纸用了 min.
(3)爷爷走去报亭的平均速度是 m/min.
400
15
40
第伍章节
课堂小结
课堂小结
变量和常量
自变量、自变量的函数
函数值
自变量的取值范围
解析式
函数
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
