人教八下19.2.2用待定系数法求一次函数解析式第3课时 课件(共39张PPT)
文档属性
| 名称 | 人教八下19.2.2用待定系数法求一次函数解析式第3课时 课件(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 12.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 00:00:00 | ||
图片预览











文档简介
(共39张PPT)
人教版数学八年级下册
第19章 一次函数
汇报人:孙老师
汇报班级:X级X班
19.2.2 第3课时 用待定系数法求一次函数解析式
19.2 一次函数
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.掌握用待定系数法求函数解析式的方法.
2.会熟练运用待定系数法在函数的实际应用中.
1. 用待定系数法确定一次函数解析式的一般步骤是:
(1)根据已知条件设出含有 的函数解析式.
(2)将x,y的对应值或将图象上的点的坐标代入所设函数解析式中,得到以待定系数为 的方程.
(3) ,求出未知待定系数的值.
(4)将求出的待定系数 所设函数解析式中.
2. 在求分段函数关系式时,要注意自变量的 ,它可用不同的函数解析式来表示,还可用图象来直观地反映.
待定系数
未知数
解方程
代回
取值范围
第贰章节
新课导入
新课导入
思考1 确定正比例函数解析式 y=kx(k≠0),需要求出几个值?需要知道几个条件?
需要求出 k 的值,知道 1 个条件即可.
正比例函数解析式 y=kx(k≠0)中 x, y 分别代表自变量和函数值,只要求出 k 的值即可确定正比例函数解析式.
思考2 确定一次函数解析式 y=kx+b(k≠0),需要求出几个值?需要知道几个条件?
需要求出 k,b 的值,知道 2 个条件即可.
一次函数解析式y=kx+b(k≠0)中x,y分别代表自变量和函数值,只要求出k ,b的值即可确定一次函数解析式.
第叁章节
新知探究
新知探究
知识点 1:用待定系数法求一次函数的解析式
如图,已知一次函数的图象经过 P (0,-1),
Q (1,1) 两点. 怎样确定这个一次函数的解析式呢?
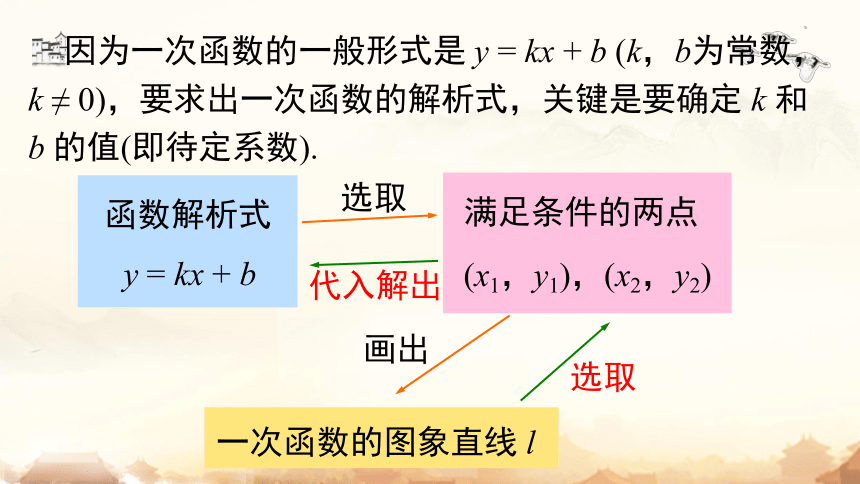
因为一次函数的一般形式是 y = kx + b (k,b为常数,k ≠ 0),要求出一次函数的解析式,关键是要确定 k 和 b 的值(即待定系数).
函数解析式
y = kx + b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的图象直线 l
选取
代入解出
画出
选取
∵ P(0,-1) 和 Q(1,1) 都在该函数图象上,
∴它们的坐标都满足 y = kx + b , 将这两点坐标代入该式中,得到一个关于 k,b 的二元一次方程组:
k · 0 + b = -1,
k + b = 1,
{
{
解这个方程组,得
k = 2,
b = -1.
∴ 这个一次函数的解析式为 y = 2x - 1.
像这样,通过先设定函数解析式(确定函数模型),再根据条件确定解析式中的未知系数,从而求出函数解析式的方法称为待定系数法.
函数解析式
y = kx + b
一次函数的图象直线 l
从数到形
从形到数
数学的基本思想方法:数形结合
待定系数法
给两点可以确定一次函数的解析式,一点可以吗 更多点呢
从几何角度来看: 一点不够, 因为两点确定一条直线.
两个及以上都可以,但是两点足够.
从代数角度来看: 一次函数的解析式中含有 k,b 两个
待定系数,因此需要两个点的坐标,列两个方程,即
得二元一次方程组.
练一练
1. 已知一次函数的图象过点 (3,5) 与 (-4,-9),
求这个一次函数的解析式.
解:设这个一次函数的解析式为 y = kx + b.
把点 (3,5) 与 (-4,-9) 分别代入,得:
∴这个一次函数的解析式为 y = 2x - 1.
解方程组得
y = kx + b (k ≠ 0)
二元一次
归纳总结
(1)设:设一次函数的一般形式 ; (2)列:把图象上的点 (x1,y1),(x2,y2) 代入一次函数的解析式,组成_________方程组;
(3)解:解二元一次方程组得 k,b;
(4)还原:把 k,b 的值代入一次函数的解析式.
总结
求一次函数解析式的步骤:
例1 若一次函数的图象经过点 A(2,0),且与直线 y = -x + 3 平行,求其解析式.
解:设这个一次函数的解析式为 y = kx + b.
k = -1,
2k + b = 0,
{
由题意得
k = -1,
b = 2.
{
解得
∴ y = - x + 2.
典例精析
2. 已知一次函数的图象过点 (0,2),且与两坐标轴围成的三角形的面积为 2,求此一次函数的解析式.
y
x
O
2
注意:此题有两种情况.
练一练
分析:一次函数 y = kx + b 与 y 轴的交点是 (0,b),与 x 轴的交点是( ,0). 由题意可列出关于 k,b 的方程.
解:设一次函数的解析式为 y = kx + b (k ≠ 0).
∵ 一次函数 y = kx + b 的图象过点(0,2),
∴ b = 2.
∵ 一次函数的图象与 x 轴的交点是( ,0),
则 解得 k = 1 或 -1.
故此一次函数的解析式为 y = x + 2 或 y = - x + 2.
知识点 2:一次函数与实际问题
购买种子 数量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
例2 “黄金1号”玉米种子的价格为 5 元/kg,如果一次购买 2 kg 以上的种子,超过 2 kg 部分的种子的价格打 8 折.
(1)填写下表:
2.5
5
7.5
10
12
14
16
18
(2) 写出购买量关于付款金额的函数解析式,并画出函数图象.
分析:从题目可知,种子的价格与 有关.
若购买种子量为 x>2 时,种子价格 y 为:
.
若购买种子量为 0≤x≤2 时,种子价格 y 为: .
购买种子量
y = 5x
y = 5×0.8(x - 2) + 10 = 4x + 2
解:设购买量为 x 千克,付款金额为 y 元.
当 x>2 时,y = 5×0.8(x - 2) + 10 = 4x + 2.
当 0≤x≤2 时,y = 5x;
(2) 写出购买量关于付款金额的函数解析式,并画出函数图象.
叫做分段函数.
注意:1.它是一个函数;
2.要写明自变量取值范围
y =
5x (0≤x≤2)
4x + 2 (x > 2)
{
y = 4x + 2 (x > 2)
y
x
O
1
2
10
3
14
的函数图象为:
y =
5x (0≤x≤2)
4x + 2 (x > 2)
{
y = 5x (0≤x≤2)
思考:你能由上面的函数解析式或函数图象解决以下问题吗?
(1) 一次购买 1.5 kg 种子,需付款多少元?
(2) 30 元最多能购买多少种子?
解析:由函数图象也能解决这些问题.
(1) 过 x 轴上表示数 1.5 的点作 x 轴的垂线与函数图象交于一点,这点的纵坐标就是需付款的钱数.
(2) 过 y 轴上表示数 30 的点作 y 轴的垂线与函数图象交于一点,这点的横坐标就是需购买种子的重量.
(1) 7.5 元.
(2) 6 kg.
练一练
3. 为节约用水,某市制定以下用水收费标准,每户每月用水不超过 8 立方米,每立方米收取 1 元外加 0.3 元的污水处理费;超过时,超过部分每立方米收取 1.5 元外加 1.2 元污水处理费,现设一户每月用水 x 立方米,应缴水费 y 元.
(1)求出 y 关于 x 的函数解析式;
解:y 关于 x 的函数解析式为:
(1 + 0.3)x = 1.3x, (0≤x≤8)
(1.5+1.2)(x-8)+1.3×8 = 2.7x - 11.2. (x>8)
y =
记得加上不超过8 立方米的费用.
(2) 当 x = 10 时,y = 2.7×10 - 11.2 = 15.8.
(3) ∵ 1.3×8 = 10.4 < 26.6,
∴ 2.7x - 11.2 = 26.6,解得 x = 14.
答:应缴水费为 15.8 元.
答:该户这月用水量为 14 立方米.
(2) 该市一户某月若用水 x = 10 立方米时,求应缴水费;
(3) 该市一户某月缴水费 26.6 元,求该户这月用水量.
∴ 该用户用水量超过 8 立方米.
第肆章节
随堂练习
随堂练习
知识点1:用待定系数法求一次函数解析式
1. 已知一次函数y=kx+b的图象经过点A(0,-2),B(1,0),则b= ,k= .
2. 若直线y=-2x+b经过点(3,2), 则直线与x轴交点的坐标是 .
3. 某一次函数y=kx+b的图象过点(0,1),且函数值y随x的增大而减小.请写一个符合上述条件的函数解析式 .
-2
2
(4,0)
y=-x+1(答案不唯一)
4. 已知一次函数的图象经过(0,3),(1,2)两点,求该一次函数的解析式.
y=-x+3
5. 已知一次函数y=kx+2,当x=5时,y=4.
(1)求这个一次函数的解析式.
(1)y=0.4x+2.
(2)求当x=-5时,函数y的值.
(2)0.
6. 点A(1,4),B(-2,m),C(6,-1)在同一条直线上,求m的值.
7.
知识点2:分段函数
7. 某自来水公司为了鼓励市民节约用水,采取分段收费标准.居民每月应交水费y(单位:元)是关于用水量x(单位:t)的函数,其图象如图所示,根据图象回答下列问题:
(第7题)
(1)分别写出当0≤x≤5和当x>5时,y关于x的函数解析式.
(1)当0≤x≤5时,y=0.72x;
当x>5时,y=0.9x-0.9.
(2)若某户居民该月用水3.5 t,问应交水费多少元?若该月交水费9元,则用水多少吨?
(2)2.52元 11 t.
8. 电力公司为鼓励市民节约用电,采取按月用电量分段收费的办法,居民每月应交电费y(单位:元)关于用电量x(单位:kW·h)的函数图象如图所示.根据图象解答下列问题:
(第8题)
(1)分别写出当0≤x≤100和x>100时,y关于x的函数解析式.
(1)当0≤x≤100时,y=0.65x;
当x>100时,y=0.8x-15.
(2)利用函数解析式,说明电力公司采取的收费标准.
(2)收费标准:用电量不超过100 kW·h时,每千瓦时按0.65元收取;若超过100 kW·h,则超过的部分按每千瓦时0.8元收取.
9. 某市出租车公司收费标准如图所示,则当x≥3时,y关于x的解析式为 .
(第9题)
y= x+
10. 某运输公司规定每名旅客的行李托运费与所托运行李质量之间的关系如图所示,请根据图象回答下列问题:
(1)由图象可知,行李质量只要不超过 kg,就可以免费携带;如果超过了规定的质量,则每超过10 kg,要付费 元.
(2)若旅客携带的行李质量为x(单位:kg),所付的行李托运费是y(单位:元),请写出y随x变化的函数解析式.
(2)y=
20
5
(第10题)
(3)若王先生携带行李50 kg,他共要付行李托运费多少元?
(3)15元.
11. 某人从离家18 km的地方回家,他离家的距离s(单位:km)关于时间t(单位:min)的函数图象如图所示.
(1)求线段AB的解析式.
解:(1)设线段AB的解析式为s=kt+b.
∵当0≤x≤6时,s=kt+b经过点(0,18)和(3,15),
∴ 解得
∴s=-t+18(0≤t≤6).
(2)此人回家用了多长时间?
(2)由图可知,直线BC经过点(6,12)和(8,8).
∴ 解得
∴线段BC的解析式是s=-2t+24.
令s=0,即-2t+24=0.解得t=12.∴此人回家用了12 min.
第伍章节
课堂小结
课堂小结
一次函数
求一次函数解析式
应用
待定系数法
①设;②列;③解;④代.
①已知一次函数解析式
②题目中未给出一次函数解析式
步骤
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
人教版数学八年级下册
第19章 一次函数
汇报人:孙老师
汇报班级:X级X班
19.2.2 第3课时 用待定系数法求一次函数解析式
19.2 一次函数
目录
壹
学习目标
贰
新课导入
叁
新知探究
肆
随堂练习
伍
课堂小结
第壹章节
学习目标
学习目标
1.掌握用待定系数法求函数解析式的方法.
2.会熟练运用待定系数法在函数的实际应用中.
1. 用待定系数法确定一次函数解析式的一般步骤是:
(1)根据已知条件设出含有 的函数解析式.
(2)将x,y的对应值或将图象上的点的坐标代入所设函数解析式中,得到以待定系数为 的方程.
(3) ,求出未知待定系数的值.
(4)将求出的待定系数 所设函数解析式中.
2. 在求分段函数关系式时,要注意自变量的 ,它可用不同的函数解析式来表示,还可用图象来直观地反映.
待定系数
未知数
解方程
代回
取值范围
第贰章节
新课导入
新课导入
思考1 确定正比例函数解析式 y=kx(k≠0),需要求出几个值?需要知道几个条件?
需要求出 k 的值,知道 1 个条件即可.
正比例函数解析式 y=kx(k≠0)中 x, y 分别代表自变量和函数值,只要求出 k 的值即可确定正比例函数解析式.
思考2 确定一次函数解析式 y=kx+b(k≠0),需要求出几个值?需要知道几个条件?
需要求出 k,b 的值,知道 2 个条件即可.
一次函数解析式y=kx+b(k≠0)中x,y分别代表自变量和函数值,只要求出k ,b的值即可确定一次函数解析式.
第叁章节
新知探究
新知探究
知识点 1:用待定系数法求一次函数的解析式
如图,已知一次函数的图象经过 P (0,-1),
Q (1,1) 两点. 怎样确定这个一次函数的解析式呢?
因为一次函数的一般形式是 y = kx + b (k,b为常数,k ≠ 0),要求出一次函数的解析式,关键是要确定 k 和 b 的值(即待定系数).
函数解析式
y = kx + b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的图象直线 l
选取
代入解出
画出
选取
∵ P(0,-1) 和 Q(1,1) 都在该函数图象上,
∴它们的坐标都满足 y = kx + b , 将这两点坐标代入该式中,得到一个关于 k,b 的二元一次方程组:
k · 0 + b = -1,
k + b = 1,
{
{
解这个方程组,得
k = 2,
b = -1.
∴ 这个一次函数的解析式为 y = 2x - 1.
像这样,通过先设定函数解析式(确定函数模型),再根据条件确定解析式中的未知系数,从而求出函数解析式的方法称为待定系数法.
函数解析式
y = kx + b
一次函数的图象直线 l
从数到形
从形到数
数学的基本思想方法:数形结合
待定系数法
给两点可以确定一次函数的解析式,一点可以吗 更多点呢
从几何角度来看: 一点不够, 因为两点确定一条直线.
两个及以上都可以,但是两点足够.
从代数角度来看: 一次函数的解析式中含有 k,b 两个
待定系数,因此需要两个点的坐标,列两个方程,即
得二元一次方程组.
练一练
1. 已知一次函数的图象过点 (3,5) 与 (-4,-9),
求这个一次函数的解析式.
解:设这个一次函数的解析式为 y = kx + b.
把点 (3,5) 与 (-4,-9) 分别代入,得:
∴这个一次函数的解析式为 y = 2x - 1.
解方程组得
y = kx + b (k ≠ 0)
二元一次
归纳总结
(1)设:设一次函数的一般形式 ; (2)列:把图象上的点 (x1,y1),(x2,y2) 代入一次函数的解析式,组成_________方程组;
(3)解:解二元一次方程组得 k,b;
(4)还原:把 k,b 的值代入一次函数的解析式.
总结
求一次函数解析式的步骤:
例1 若一次函数的图象经过点 A(2,0),且与直线 y = -x + 3 平行,求其解析式.
解:设这个一次函数的解析式为 y = kx + b.
k = -1,
2k + b = 0,
{
由题意得
k = -1,
b = 2.
{
解得
∴ y = - x + 2.
典例精析
2. 已知一次函数的图象过点 (0,2),且与两坐标轴围成的三角形的面积为 2,求此一次函数的解析式.
y
x
O
2
注意:此题有两种情况.
练一练
分析:一次函数 y = kx + b 与 y 轴的交点是 (0,b),与 x 轴的交点是( ,0). 由题意可列出关于 k,b 的方程.
解:设一次函数的解析式为 y = kx + b (k ≠ 0).
∵ 一次函数 y = kx + b 的图象过点(0,2),
∴ b = 2.
∵ 一次函数的图象与 x 轴的交点是( ,0),
则 解得 k = 1 或 -1.
故此一次函数的解析式为 y = x + 2 或 y = - x + 2.
知识点 2:一次函数与实际问题
购买种子 数量/kg 0.5 1 1.5 2 2.5 3 3.5 4 …
付款金额/元 …
例2 “黄金1号”玉米种子的价格为 5 元/kg,如果一次购买 2 kg 以上的种子,超过 2 kg 部分的种子的价格打 8 折.
(1)填写下表:
2.5
5
7.5
10
12
14
16
18
(2) 写出购买量关于付款金额的函数解析式,并画出函数图象.
分析:从题目可知,种子的价格与 有关.
若购买种子量为 x>2 时,种子价格 y 为:
.
若购买种子量为 0≤x≤2 时,种子价格 y 为: .
购买种子量
y = 5x
y = 5×0.8(x - 2) + 10 = 4x + 2
解:设购买量为 x 千克,付款金额为 y 元.
当 x>2 时,y = 5×0.8(x - 2) + 10 = 4x + 2.
当 0≤x≤2 时,y = 5x;
(2) 写出购买量关于付款金额的函数解析式,并画出函数图象.
叫做分段函数.
注意:1.它是一个函数;
2.要写明自变量取值范围
y =
5x (0≤x≤2)
4x + 2 (x > 2)
{
y = 4x + 2 (x > 2)
y
x
O
1
2
10
3
14
的函数图象为:
y =
5x (0≤x≤2)
4x + 2 (x > 2)
{
y = 5x (0≤x≤2)
思考:你能由上面的函数解析式或函数图象解决以下问题吗?
(1) 一次购买 1.5 kg 种子,需付款多少元?
(2) 30 元最多能购买多少种子?
解析:由函数图象也能解决这些问题.
(1) 过 x 轴上表示数 1.5 的点作 x 轴的垂线与函数图象交于一点,这点的纵坐标就是需付款的钱数.
(2) 过 y 轴上表示数 30 的点作 y 轴的垂线与函数图象交于一点,这点的横坐标就是需购买种子的重量.
(1) 7.5 元.
(2) 6 kg.
练一练
3. 为节约用水,某市制定以下用水收费标准,每户每月用水不超过 8 立方米,每立方米收取 1 元外加 0.3 元的污水处理费;超过时,超过部分每立方米收取 1.5 元外加 1.2 元污水处理费,现设一户每月用水 x 立方米,应缴水费 y 元.
(1)求出 y 关于 x 的函数解析式;
解:y 关于 x 的函数解析式为:
(1 + 0.3)x = 1.3x, (0≤x≤8)
(1.5+1.2)(x-8)+1.3×8 = 2.7x - 11.2. (x>8)
y =
记得加上不超过8 立方米的费用.
(2) 当 x = 10 时,y = 2.7×10 - 11.2 = 15.8.
(3) ∵ 1.3×8 = 10.4 < 26.6,
∴ 2.7x - 11.2 = 26.6,解得 x = 14.
答:应缴水费为 15.8 元.
答:该户这月用水量为 14 立方米.
(2) 该市一户某月若用水 x = 10 立方米时,求应缴水费;
(3) 该市一户某月缴水费 26.6 元,求该户这月用水量.
∴ 该用户用水量超过 8 立方米.
第肆章节
随堂练习
随堂练习
知识点1:用待定系数法求一次函数解析式
1. 已知一次函数y=kx+b的图象经过点A(0,-2),B(1,0),则b= ,k= .
2. 若直线y=-2x+b经过点(3,2), 则直线与x轴交点的坐标是 .
3. 某一次函数y=kx+b的图象过点(0,1),且函数值y随x的增大而减小.请写一个符合上述条件的函数解析式 .
-2
2
(4,0)
y=-x+1(答案不唯一)
4. 已知一次函数的图象经过(0,3),(1,2)两点,求该一次函数的解析式.
y=-x+3
5. 已知一次函数y=kx+2,当x=5时,y=4.
(1)求这个一次函数的解析式.
(1)y=0.4x+2.
(2)求当x=-5时,函数y的值.
(2)0.
6. 点A(1,4),B(-2,m),C(6,-1)在同一条直线上,求m的值.
7.
知识点2:分段函数
7. 某自来水公司为了鼓励市民节约用水,采取分段收费标准.居民每月应交水费y(单位:元)是关于用水量x(单位:t)的函数,其图象如图所示,根据图象回答下列问题:
(第7题)
(1)分别写出当0≤x≤5和当x>5时,y关于x的函数解析式.
(1)当0≤x≤5时,y=0.72x;
当x>5时,y=0.9x-0.9.
(2)若某户居民该月用水3.5 t,问应交水费多少元?若该月交水费9元,则用水多少吨?
(2)2.52元 11 t.
8. 电力公司为鼓励市民节约用电,采取按月用电量分段收费的办法,居民每月应交电费y(单位:元)关于用电量x(单位:kW·h)的函数图象如图所示.根据图象解答下列问题:
(第8题)
(1)分别写出当0≤x≤100和x>100时,y关于x的函数解析式.
(1)当0≤x≤100时,y=0.65x;
当x>100时,y=0.8x-15.
(2)利用函数解析式,说明电力公司采取的收费标准.
(2)收费标准:用电量不超过100 kW·h时,每千瓦时按0.65元收取;若超过100 kW·h,则超过的部分按每千瓦时0.8元收取.
9. 某市出租车公司收费标准如图所示,则当x≥3时,y关于x的解析式为 .
(第9题)
y= x+
10. 某运输公司规定每名旅客的行李托运费与所托运行李质量之间的关系如图所示,请根据图象回答下列问题:
(1)由图象可知,行李质量只要不超过 kg,就可以免费携带;如果超过了规定的质量,则每超过10 kg,要付费 元.
(2)若旅客携带的行李质量为x(单位:kg),所付的行李托运费是y(单位:元),请写出y随x变化的函数解析式.
(2)y=
20
5
(第10题)
(3)若王先生携带行李50 kg,他共要付行李托运费多少元?
(3)15元.
11. 某人从离家18 km的地方回家,他离家的距离s(单位:km)关于时间t(单位:min)的函数图象如图所示.
(1)求线段AB的解析式.
解:(1)设线段AB的解析式为s=kt+b.
∵当0≤x≤6时,s=kt+b经过点(0,18)和(3,15),
∴ 解得
∴s=-t+18(0≤t≤6).
(2)此人回家用了多长时间?
(2)由图可知,直线BC经过点(6,12)和(8,8).
∴ 解得
∴线段BC的解析式是s=-2t+24.
令s=0,即-2t+24=0.解得t=12.∴此人回家用了12 min.
第伍章节
课堂小结
课堂小结
一次函数
求一次函数解析式
应用
待定系数法
①设;②列;③解;④代.
①已知一次函数解析式
②题目中未给出一次函数解析式
步骤
人教版数学八年级下册
汇报人:孙老师
汇报班级:X级X班
谢谢观看
