高一下数学人教A版2019必修第二册 6.2.3 向量的数乘运算(共22张PPT)
文档属性
| 名称 | 高一下数学人教A版2019必修第二册 6.2.3 向量的数乘运算(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 13:11:13 | ||
图片预览







文档简介
6.2.3 向量的数乘运算
1.通过实例分析,掌握平面向量数乘运算及运算规则,理解其几何意义;
2.理解两个平面向量共线的含义;
3.了解平面向量的线性运算性质及其几何意义.
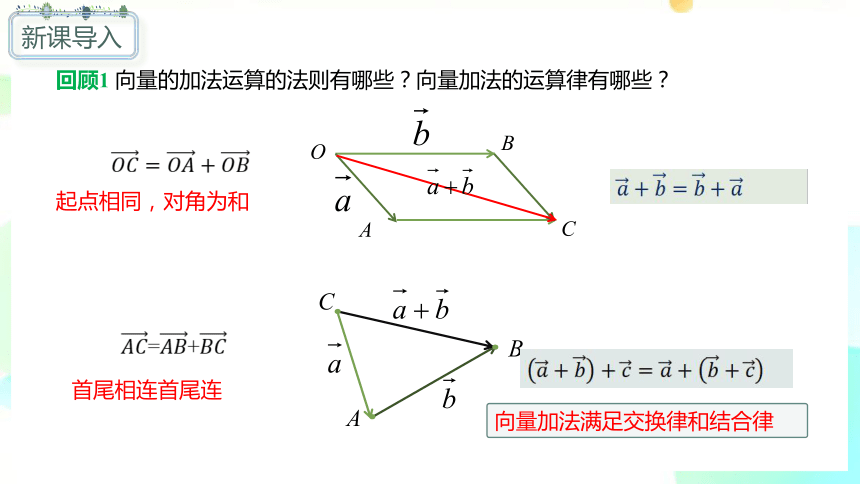
回顾1 向量的加法运算的法则有哪些?向量加法的运算律有哪些?
O
A
B
C
????????=????????+????????
?
起点相同,对角为和
????????=????????+????????
?
首尾相连首尾连
????+????= ????+????
?
????+????+????=????+????+????
?
向量加法满足交换律和结合律
回顾2 向量的减法是如何描述的?它的几何意义是怎样的?
向量的减法:?????????=????+(?????)
?
自然语言:减去一个向量等于加上这个向量的相反向量.
首同尾连向被减:????????=?????????0????
?
即?????????可以表示为从向量????的终点指向向量????的终点的向量
这就是向量减法的几何意义
?
1.向量的加法运算:
①三角形法则:首尾相接,首指向尾
②平行四边形法则:起点相同,对角为和
2.向量的减法运算:共起点,连终点,指被减
思考:向量有乘法运算吗?怎么定义呢?运算结果是什么量呢?
问题1 我们已经学习了向量的加法,请同学们作出????+????+????和?????+?????+?????,并请同学们指出相加后和的长度与方向有什么变化?
这些变化与那些因素有关?
?
一、向量的数乘运算及其几何意义
B
C
O
A
如图,?????????=????????+????????+????????=????+????+?????.
类比数的乘法,我们把 ????+????+????记作 3?????,即?????????=3????.
显然3????的方向与????的方向相同,
3???? 的长度是????的长度的3倍,即3????=3????.
?
N
M
Q
P
类似的,?????????=????????+????????+????????=?????+?????+?????.
我们把?????+?????+?????记作 ?3?????,即?????????=?3????.
显然3????的方向与????的方向相反,
?3???? 的长度是????的长度的3倍,即?3????=3????.
?
一般地,我们规定实数????与向量????的积是一个向量, 这种运算叫做向量的数乘,记作?????????.
?
长度: ????????=????????
方向:当????>0时,????????的方向与????的方向相同;
当????<0时, ????????的方向与????的方向相反;
当????=0时, ????????=0
?
注:1.向量数乘的结果仍然是向量;所得的向量的方向由????与????决定;
2.实数和向量可以相乘,但不能相加减
?
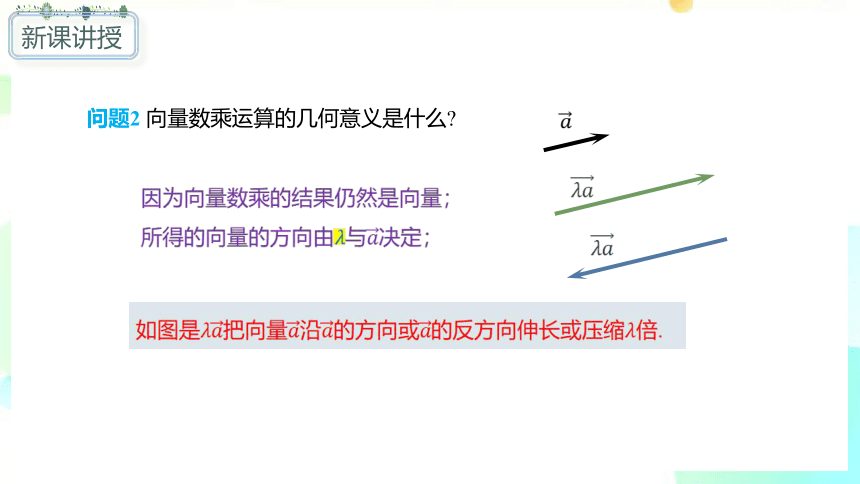
问题2 向量数乘运算的几何意义是什么?
????
?
????????
?
????????
?
因为向量数乘的结果仍然是向量;
所得的向量的方向由????与????决定;
?
如图是????????把向量????沿????的方向或????的反方向伸长或压缩????倍.
?
????
?
????????
?
????????
?
(1)当????>0时,????????的方向与????的方向相同;
(2)当????<0时, ????????的方向与????的方向相反;
(3)当????=0时, ????????=0(若????=0, ????????=0也成立)
?
相反向量: ?1????=?????;
零向量: ????=0或????=0? ????????=0
?
相反向量与零向量的另一种解释方式
问题3 数的乘法满足交换律、结合律和分配律,向量的数乘运算是否也满足上述运算律呢?
设????,????是实数,那么有
(1)????????????=????????????
(2)????+????????=????????+????????
(3)????(????+????)=????????+????????
?
二、数乘运算的运算律及其线性运算
向量数乘的运算律:
设????,????是实数,那么有
(1)结合律:????????????=????????????
(2)分配律:①????+????????=????????+????????
②????(????+????)=????????+????????
?
特别地,我们有(?????)????=?????????=????(?????)
????(?????????)=?????????????????
?
向量的线性运算:
向量的加、减、数乘运算统称为向量的线性运算.
向量线性运算的结果仍是向量.
推广:对于任意向量????,????,以及对于任意实数????,????1,????2,恒有????(????1????+????2????)=????????1????+????????2????)
?
例5:计算(1)(?3)×4????
(2)3(????+????)?2(?????????)?????
(3)(2????+3?????????)?(3?????2????+????)
?
解:1原式=?3×4????=?12????
?
2原式=3????+3?????2????+2?????????= 5????
?
3原式=2????+3??????????3????+2?????????=?????+5?????2????
?
例6:如图,平行四边形?????????????????的两条对角线相交于点M,且????????=????,????????=???? ,
用????,????表示????????,????????,????????和????????.
?
????
?
????
?
A
B
C
D
M
向量的拆拆凑凑
解:在????????????????中, ????????=????????+????????=????+????,????????=?????????????????=?????????
由平行四边形的两条对角线互相平分,得
????????=12????????=?12????????=?12(????????+????????)=?12?????12????
????????=12????????=12(?????????????????)=12?????12????
????????=12????????=12????????=12(????????+????????)=12????+12????
????????=12????????=12(?????????????????)=12?????12????
?
思考2:引入向量数乘运算后,你能发现实数与向量的积与原向量之间的位置关系吗?
向量的数乘:实数????与向量????的积是一个向量,记作?????????.
?
(1)当????>0时,????????的方向与????的方向相同;
(2)当????<0时, ????????的方向与????的方向相反;
(3)当????=0时, ????????=0(若????=0, ????????=0也成立)
?
????????与????这两个是共线的
?
三、平面向量共线定理
实数与向量的积与原向量共线
????????与????这两个是共线的
?
事实上,对于向量????( ?????≠ 0), ?????,如果有一个实数????,使????=????????,那么由向量数乘的定义可知????与????共线.
反过来,已知向量????与????共线,且向量????的长度是向量????的长度的????倍,即 ????=????????,那么当????与????同方向时,有????=?????????;当????与????反方向时,有????=??????????
?
向量共线定理:
向量????( ?????≠ 0)与??????共线的充要条件是:存在唯一一个实数????,使????=????????
?
根据这一定理,设非零向量????位于直线????上,那么对于直线????上的任意一个向量?????, 都存在唯一的一个实数????,使????=?????????.也就是说,位于同一直线上的向量可以由位于这条直线上的一个非零向量表示.
?
例7.如图,已知任意两个非零向量????,?????,试作向量????????=????+????, ????????=????+2????, ????????=????+3???? ,猜想????,????,????三点之间的位置关系,并证明你的猜想.
?
分别作向量????????, ????????, ????????,过点????,????作直线???????? 观察发现,不论向量????,????怎样变化,点????始终在直线????????上,猜想????,????,????三点共线.
事实上,因为
????????=???????????????????= ????+2?????????+????= ?????;
????????=???????????????????= ????+3?????????+????=2?????
所以,????????=2????????,
因此,????,????,????三点共线,
?
例8.如图,已知????,?????是两个不共线的向量??????????????,12?????32????共线,求实数????的值.
?
由????,????不共线,易知12?????32????为非零向量.
由向量??????????????,12?????32????共线可知,
存在实数????,使得?????????????=????12?????32????,即????+12????????=32????+1????.
由????,????不共线,必有????+12????=32????+1=0,
否则,不妨设 ????+12????≠0,则????=32????+1????+12????????
由两个向量共线的充要条件可知, ????,????会共线,与已知矛盾.
由????+12????=032????+1=0,解得????=13
因此,当向量??????????????,12?????32????共线时, ????=13
?
(1)向量的数乘运算及其几何意义
(2)数乘的运算律与向量的线性运算的概念
(3)共线向量定理
1.通过实例分析,掌握平面向量数乘运算及运算规则,理解其几何意义;
2.理解两个平面向量共线的含义;
3.了解平面向量的线性运算性质及其几何意义.
回顾1 向量的加法运算的法则有哪些?向量加法的运算律有哪些?
O
A
B
C
????????=????????+????????
?
起点相同,对角为和
????????=????????+????????
?
首尾相连首尾连
????+????= ????+????
?
????+????+????=????+????+????
?
向量加法满足交换律和结合律
回顾2 向量的减法是如何描述的?它的几何意义是怎样的?
向量的减法:?????????=????+(?????)
?
自然语言:减去一个向量等于加上这个向量的相反向量.
首同尾连向被减:????????=?????????0????
?
即?????????可以表示为从向量????的终点指向向量????的终点的向量
这就是向量减法的几何意义
?
1.向量的加法运算:
①三角形法则:首尾相接,首指向尾
②平行四边形法则:起点相同,对角为和
2.向量的减法运算:共起点,连终点,指被减
思考:向量有乘法运算吗?怎么定义呢?运算结果是什么量呢?
问题1 我们已经学习了向量的加法,请同学们作出????+????+????和?????+?????+?????,并请同学们指出相加后和的长度与方向有什么变化?
这些变化与那些因素有关?
?
一、向量的数乘运算及其几何意义
B
C
O
A
如图,?????????=????????+????????+????????=????+????+?????.
类比数的乘法,我们把 ????+????+????记作 3?????,即?????????=3????.
显然3????的方向与????的方向相同,
3???? 的长度是????的长度的3倍,即3????=3????.
?
N
M
Q
P
类似的,?????????=????????+????????+????????=?????+?????+?????.
我们把?????+?????+?????记作 ?3?????,即?????????=?3????.
显然3????的方向与????的方向相反,
?3???? 的长度是????的长度的3倍,即?3????=3????.
?
一般地,我们规定实数????与向量????的积是一个向量, 这种运算叫做向量的数乘,记作?????????.
?
长度: ????????=????????
方向:当????>0时,????????的方向与????的方向相同;
当????<0时, ????????的方向与????的方向相反;
当????=0时, ????????=0
?
注:1.向量数乘的结果仍然是向量;所得的向量的方向由????与????决定;
2.实数和向量可以相乘,但不能相加减
?
问题2 向量数乘运算的几何意义是什么?
????
?
????????
?
????????
?
因为向量数乘的结果仍然是向量;
所得的向量的方向由????与????决定;
?
如图是????????把向量????沿????的方向或????的反方向伸长或压缩????倍.
?
????
?
????????
?
????????
?
(1)当????>0时,????????的方向与????的方向相同;
(2)当????<0时, ????????的方向与????的方向相反;
(3)当????=0时, ????????=0(若????=0, ????????=0也成立)
?
相反向量: ?1????=?????;
零向量: ????=0或????=0? ????????=0
?
相反向量与零向量的另一种解释方式
问题3 数的乘法满足交换律、结合律和分配律,向量的数乘运算是否也满足上述运算律呢?
设????,????是实数,那么有
(1)????????????=????????????
(2)????+????????=????????+????????
(3)????(????+????)=????????+????????
?
二、数乘运算的运算律及其线性运算
向量数乘的运算律:
设????,????是实数,那么有
(1)结合律:????????????=????????????
(2)分配律:①????+????????=????????+????????
②????(????+????)=????????+????????
?
特别地,我们有(?????)????=?????????=????(?????)
????(?????????)=?????????????????
?
向量的线性运算:
向量的加、减、数乘运算统称为向量的线性运算.
向量线性运算的结果仍是向量.
推广:对于任意向量????,????,以及对于任意实数????,????1,????2,恒有????(????1????+????2????)=????????1????+????????2????)
?
例5:计算(1)(?3)×4????
(2)3(????+????)?2(?????????)?????
(3)(2????+3?????????)?(3?????2????+????)
?
解:1原式=?3×4????=?12????
?
2原式=3????+3?????2????+2?????????= 5????
?
3原式=2????+3??????????3????+2?????????=?????+5?????2????
?
例6:如图,平行四边形?????????????????的两条对角线相交于点M,且????????=????,????????=???? ,
用????,????表示????????,????????,????????和????????.
?
????
?
????
?
A
B
C
D
M
向量的拆拆凑凑
解:在????????????????中, ????????=????????+????????=????+????,????????=?????????????????=?????????
由平行四边形的两条对角线互相平分,得
????????=12????????=?12????????=?12(????????+????????)=?12?????12????
????????=12????????=12(?????????????????)=12?????12????
????????=12????????=12????????=12(????????+????????)=12????+12????
????????=12????????=12(?????????????????)=12?????12????
?
思考2:引入向量数乘运算后,你能发现实数与向量的积与原向量之间的位置关系吗?
向量的数乘:实数????与向量????的积是一个向量,记作?????????.
?
(1)当????>0时,????????的方向与????的方向相同;
(2)当????<0时, ????????的方向与????的方向相反;
(3)当????=0时, ????????=0(若????=0, ????????=0也成立)
?
????????与????这两个是共线的
?
三、平面向量共线定理
实数与向量的积与原向量共线
????????与????这两个是共线的
?
事实上,对于向量????( ?????≠ 0), ?????,如果有一个实数????,使????=????????,那么由向量数乘的定义可知????与????共线.
反过来,已知向量????与????共线,且向量????的长度是向量????的长度的????倍,即 ????=????????,那么当????与????同方向时,有????=?????????;当????与????反方向时,有????=??????????
?
向量共线定理:
向量????( ?????≠ 0)与??????共线的充要条件是:存在唯一一个实数????,使????=????????
?
根据这一定理,设非零向量????位于直线????上,那么对于直线????上的任意一个向量?????, 都存在唯一的一个实数????,使????=?????????.也就是说,位于同一直线上的向量可以由位于这条直线上的一个非零向量表示.
?
例7.如图,已知任意两个非零向量????,?????,试作向量????????=????+????, ????????=????+2????, ????????=????+3???? ,猜想????,????,????三点之间的位置关系,并证明你的猜想.
?
分别作向量????????, ????????, ????????,过点????,????作直线???????? 观察发现,不论向量????,????怎样变化,点????始终在直线????????上,猜想????,????,????三点共线.
事实上,因为
????????=???????????????????= ????+2?????????+????= ?????;
????????=???????????????????= ????+3?????????+????=2?????
所以,????????=2????????,
因此,????,????,????三点共线,
?
例8.如图,已知????,?????是两个不共线的向量??????????????,12?????32????共线,求实数????的值.
?
由????,????不共线,易知12?????32????为非零向量.
由向量??????????????,12?????32????共线可知,
存在实数????,使得?????????????=????12?????32????,即????+12????????=32????+1????.
由????,????不共线,必有????+12????=32????+1=0,
否则,不妨设 ????+12????≠0,则????=32????+1????+12????????
由两个向量共线的充要条件可知, ????,????会共线,与已知矛盾.
由????+12????=032????+1=0,解得????=13
因此,当向量??????????????,12?????32????共线时, ????=13
?
(1)向量的数乘运算及其几何意义
(2)数乘的运算律与向量的线性运算的概念
(3)共线向量定理
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
