高一下数学人教A版2019必修第二册 6.2.4 课时1 向量数量积概念(共23张PPT)
文档属性
| 名称 | 高一下数学人教A版2019必修第二册 6.2.4 课时1 向量数量积概念(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 13:12:04 | ||
图片预览





文档简介
6.2.4 课时1 向量数量积概念
1.了解向量数量积的物理背景,即物体在力F的作用下产生位移s所做的功.
2.掌握向量数量积的定义及投影向量.
3.会计算平面向量的数量积.
情境1:在物理课中我们学过功的概念,那么右图中力????对小车所做的功是?
?
前面我们学习了向量的加、减运算.类比数的运算,出现了一个自然的问题:向量能否相乘?如果能,那么向量的乘法该怎样定义?
在物理课中我们学过功的概念:如果一个物体在力????的作用下产生位移????,那么力????所做的功????=|????||????|???????????? ????,其中????是????与????的夹角.
功是一个标量,它由力和位移两个向量来确定.这给我们一种启示,能否把“功”看成是两个向量“相乘”的结果呢?受此启发,我们引入向量“数量积”的概念.
?
因为力做功的计算公式中涉及力与位移的夹角,所以我们先要定义向量的夹角概念.
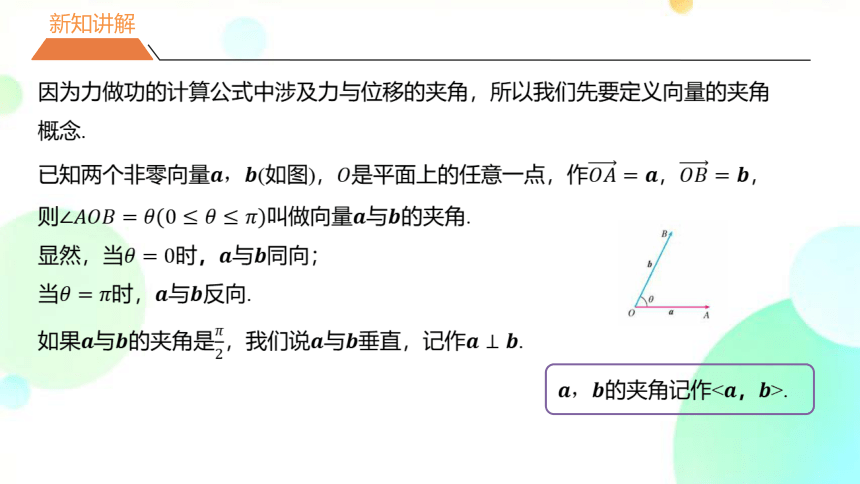
已知两个非零向量????,????(如图),????是平面上的任意一点,作????????=????,????????=????,则∠????????????=????(0≤????≤????)叫做向量????与????的夹角.
显然,当????=0时,????与????同向;
当????=????时,????与????反向.
如果????与????的夹角是????2,我们说????与????垂直,记作????⊥????.
?
????,????的夹角记作.
?
已知两个非零向量????与????,它们的夹角为????,我们把数量|????||????|????????????????叫做向量????与????的数量积(或内积),记作?????????,即?????????=|????||????|????????????????.
?
规定:零向量与任一向量的数量积为0.
对比向量的线性运算,我们发现,向量线性运算的结果是一个向量,而两个向量的数量积是一个数量,这个数量的大小与两个向量的长度及其夹角有关.
注:(1)?????????是两个向量的数量积,书写时要严格区分.符号“?”是一种运算符号,既不能省略,也不能用“×”代替.
(2)?????????是一个实数,而不是向量.
?
例9.已知|????|=5,|????|=4,????与????的夹角????=2????3,求?????????.
?
解:?????????=|????|||????|????????????????
=5×4×????????????2????3
=5×4×(?12)
=?10.
?
例10.设|????|=12,|????|=9,?????????=?542,求????与????的夹角????.
?
解:由?????????=|????|||????|????????????????,得
????????????????=?????????|????|||????|=?54212×9=?22.
因为????∈[0,????],所以????=3????4.
?
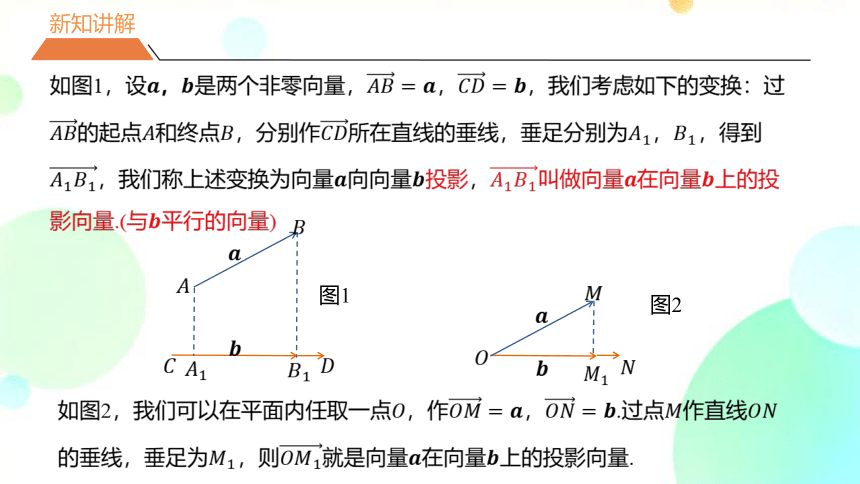
如图1,设????,????是两个非零向量,????????=????,????????=????,我们考虑如下的变换:过????????的起点????和终点????,分别作????????所在直线的垂线,垂足分别为????1,????1,得到????1????1,我们称上述变换为向量????向向量????投影,????1????1叫做向量????在向量????上的投影向量.(与????平行的向量)
?
????
?
????1
?
????
?
????
?
????
?
????1
?
????
?
????
?
图1
????
?
????
?
????
?
????
?
????
?
????1
?
图2
如图2,我们可以在平面内任取一点????,作????????=????,????????=????.过点????作直线????????的垂线,垂足为????1,则????????1就是向量????在向量????上的投影向量.
?
思考1:如图,设与????方向相同的单位向量为????,????与????的夹角为????,那么????????1与????,????,????之间有怎样的关系?
?
????
?
????
?
????
?
????
?
M
????1
?
图1
????
?
显然,????????1与????共线,于是????????1=????????.
下面我们探究????与????,????的关系,进而给出????????1的明确表达式.我们分????为锐角、直角、钝角以及????=0,????=????等情况进行讨论.
当????为锐角(如图1)时,????????1与????方向相同,????=|????????1|=|????|???????????? ????,
所以????????1=|????????1|????=|????|???????????? ???? ????;
?
当????为直角(如图2)时,????=0,所以????????1=????=|????|???????????? ????2 ????;
当????为钝角(如图3)时,????????1与????方向相反,
所以????=?|????????1|=?|????|???????????? ∠????????????1=?|????|????????????(?????????)=|????|???????????? ???? ,
即????????1=|????|???????????? ????????.
?
????
?
????
?
????
?
????
?
????
?
????1
?
图2
????
?
????
?
????
?
????
?
????
?
????
?
????1
?
图3
????
?
当????=0时,????=|????|,所以????????1=|????|????=|????|???????????? 0 ????;
当????=????时,????=?|????|,所以????????1=?|????|????=?|????|???????????? ???? ????.
从上面的讨论可知,对于任意的????∈[0,????],都有????????1=|????|???????????? ???? ????.
?
思考2:从上面的探究我们看到,两个非零向量????与????相互平行或垂直时,向量????在向量????上的投影向量具有特殊性.这时,它们的数量积又有怎样的特殊性?
?
由向量数量积的定义,可以得到向量数量积的如下重要性质.
设????,????是非零向量,它们的夹角是????,????是与????方向相同的单位向量,则
(1)?????????=?????????=|????|???????????? ????.
(2)????⊥??????????????=0.
(3)当????与????同向时,?????????=|????||????|;当????与????反向时,?????????=?|????||????|.
特别地,?????????=|????|2或|????|=?????????.
此外,由|???????????? ????|≤1还可以得到
(4)|?????????|≤|????||????|.
?
思考3:如果?????????=0,是否有????=????,或????=?????
不一定,还有可能????=????2.
?
注:?????????常常记作????2.
?
辨析:判断正误.
1.两个向量的数量积是一个向量. ( )
2.向量????在向量????上的投影向量一定与????共线. ( )
3.若?????????<0,则????与????的夹角为钝角. ( )
4.若????≠????,则对任一非零向量????都有?????????≠0. ( )
?
×
×
×
√
题型一:向量数量积的基本计算
例1.已知|????|=6,|????|=5,分别根据下列条件计算????与????的数量积:
(1)????//????;(2)????⊥????;(3)????与????的夹角为60°.
?
解:设????与????的夹角为????.
(1)当????//????时,若????与????同向,则????=0,?????????=|????||????|???????????? 0=6×5=30;
若????与????反向,则????=180°,?????????=|????||????|???????????? 180°=6×5×(?1)=?30.
(2)当????⊥????时,????与????的夹角为90°,?????????=|????||????|???????????? 90°=0.
(3)当????与????的夹角为60°时,?????????=|????||????|???????????? 60°=6×5×12=15.
?
1.已知正三角形????????????的边长为1,求:
(1)?????????????????;(2)?????????????????;(3)?????????????????.
?
解:(1)∵????????与????????的夹角为60°,
∴?????????????????=|????????||????????|???????????? 60°=1×1×12=12.
(2)∵????????与????????的夹角为120°,
∴?????????????????=|????????||????????|???????????? 120°=1×1×(?12)=?12.
(3)∵????????与????????的夹角为60°,
∴?????????????????=|????????||????????|???????????? 60°=1×1×12=12.
?
方法技巧:
利用定义法求平面向量的数量积,关键是找到两向量的模以及夹角,直接利用公式?????????=|????||????|???????????? ????求解.
?
题型二:投影向量的计算
例2.在等腰三角形????????????中,????????=????????=2,∠????????????=30°,????为????????的中点.
(1)求????????在????????上的投影向量;(2)求????????在????????上的投影向量的长度.
?
解:如图,连接????????.因为?????????????为等腰三角形,且????为????????的中点,所以????????⊥????????.
又????????=2,∠????????????=30°,所以????????=????????=????????×???????????? 30°=3.
由图可知????????与????????的夹角为∠????????????的补角,
所以????????与????????的夹角为150°.
(1)????????在????????上的投影向量为|????????|???????????? 150°?????????|????????|=2×(?32)×????????3=?????????.
(2)????????在????????上的投影向量为|????????||???????????? 150°|=3×32=32.
?
????
?
????
?
????
?
????
?
解:由已知得向量????在向量????上的投影向量的模为|????|???????????? 45°=3× 22= 322 .
?
2.已知|????|=3,|????|=5,????与????的夹角为45°,则向量????在向量????上的投影向量的模为( ).
A. 322 B.3 C.4 D.5
?
A
投影向量的求解策略
求投影向量要搞清楚是求哪一个向量在哪一个向量上的投影向量,在正确理解其定义的同时,找准两向量之间的夹角是关键,确定两向量的夹角时,一定要注意“共起点”.
题型三:平面向量的夹角
例3.已知|????|=|????|=2,且????与????的夹角为60°,则????+????与????的夹角是多少??????????与????的夹角又是多少?
?
解:如图所示,作????????=????,????????=????,且∠????????????=60°.
以????????,????????为邻边作平行四边形????????????????,则????????=????+????,????????=?????????.
因为|????|=|????|=2,所以平行四边形????????????????是菱形,
又∠????????????=60°,
所以????????与????????的夹角为30°,????????与????????的夹角为60°,
即????+????与????的夹角是30°,?????????与????的夹角是60°.
?
????
?
????
?
????
?
????
?
????
?
????
?
3.在?????????????中,∠????=90°,????????=12????????,则????????与????????的夹角是( ).
A.30° B.60° C.120° D.150°
?
解:如图,作向量????????=????????,则∠????????????是????????与????????的夹角,在?????????????中,因为∠????????????=90°,????????=12????????,所以∠????????????=60°,所以∠????????????=120°,即????????与????????的夹角是120°.
?
A
?
D
?
C
?
B
?
C
(1)求两个向量的夹角的关键是利用平移的方法使两个向量的起点重合,作两个向量的夹角,按照“一作二证三算”的步骤求出.
(2)特别地,????与????的夹角为????,????1????与????2????(????1,????2是非零常数)的夹角为????0,当????1????2<0时,????0=180°?????;当????1????2>0时,????0=????.
?
向量的夹角
(1)定义:已知两个非零向量????,????(如图),????是平面上的任意一点,作????????=????,????????=????,则∠????????????=????(0≤????≤????)叫做向量????与????的夹角.
(2)当????=0时,????与????同向;当????=????时,????与????反向.
如果????与????的夹角是????2,我们说????与????垂直,记作????⊥????.
?
向量的数量积及其几何意义
(1)定义:已知两个非零向量????与????,它们的夹角为????,我们把数量|????||????|????????????????叫做向量????与????的数量积(或内积),记作?????????,即?????????=|????||????|????????????????.
规定:零向量与任一向量的数量积为0.
(2)投影:设????,????是两个非零向量,????????=????,????????=????,我们考虑如下的变换:过????????的起点????和终点????,分别作????????所在直线的垂线,垂足分别为????1,????1,得到????1????1,我们称上述变换为向量????向向量????投影,????1????1叫做向量????在向量????上的投影向量.
?
????
?
????1
?
????
?
????
?
????
?
????1
?
????
?
????
?
向量数量积的性质
设????,????是非零向量,它们的夹角是????,????是与????方向相同的单位向量,则
(1)?????????=?????????=|????|???????????? ????.
(2)????⊥??????????????=0.
(3)当????与????同向时,?????????=|????||????|;当????与????反向时,?????????=?|????||????|.
特别地,?????????=|????|2或|????|=?????????.
此外,由|???????????? ????|≤1还可以得到
(4)|?????????|≤|????||????|.
1.了解向量数量积的物理背景,即物体在力F的作用下产生位移s所做的功.
2.掌握向量数量积的定义及投影向量.
3.会计算平面向量的数量积.
情境1:在物理课中我们学过功的概念,那么右图中力????对小车所做的功是?
?
前面我们学习了向量的加、减运算.类比数的运算,出现了一个自然的问题:向量能否相乘?如果能,那么向量的乘法该怎样定义?
在物理课中我们学过功的概念:如果一个物体在力????的作用下产生位移????,那么力????所做的功????=|????||????|???????????? ????,其中????是????与????的夹角.
功是一个标量,它由力和位移两个向量来确定.这给我们一种启示,能否把“功”看成是两个向量“相乘”的结果呢?受此启发,我们引入向量“数量积”的概念.
?
因为力做功的计算公式中涉及力与位移的夹角,所以我们先要定义向量的夹角概念.
已知两个非零向量????,????(如图),????是平面上的任意一点,作????????=????,????????=????,则∠????????????=????(0≤????≤????)叫做向量????与????的夹角.
显然,当????=0时,????与????同向;
当????=????时,????与????反向.
如果????与????的夹角是????2,我们说????与????垂直,记作????⊥????.
?
????,????的夹角记作.
?
已知两个非零向量????与????,它们的夹角为????,我们把数量|????||????|????????????????叫做向量????与????的数量积(或内积),记作?????????,即?????????=|????||????|????????????????.
?
规定:零向量与任一向量的数量积为0.
对比向量的线性运算,我们发现,向量线性运算的结果是一个向量,而两个向量的数量积是一个数量,这个数量的大小与两个向量的长度及其夹角有关.
注:(1)?????????是两个向量的数量积,书写时要严格区分.符号“?”是一种运算符号,既不能省略,也不能用“×”代替.
(2)?????????是一个实数,而不是向量.
?
例9.已知|????|=5,|????|=4,????与????的夹角????=2????3,求?????????.
?
解:?????????=|????|||????|????????????????
=5×4×????????????2????3
=5×4×(?12)
=?10.
?
例10.设|????|=12,|????|=9,?????????=?542,求????与????的夹角????.
?
解:由?????????=|????|||????|????????????????,得
????????????????=?????????|????|||????|=?54212×9=?22.
因为????∈[0,????],所以????=3????4.
?
如图1,设????,????是两个非零向量,????????=????,????????=????,我们考虑如下的变换:过????????的起点????和终点????,分别作????????所在直线的垂线,垂足分别为????1,????1,得到????1????1,我们称上述变换为向量????向向量????投影,????1????1叫做向量????在向量????上的投影向量.(与????平行的向量)
?
????
?
????1
?
????
?
????
?
????
?
????1
?
????
?
????
?
图1
????
?
????
?
????
?
????
?
????
?
????1
?
图2
如图2,我们可以在平面内任取一点????,作????????=????,????????=????.过点????作直线????????的垂线,垂足为????1,则????????1就是向量????在向量????上的投影向量.
?
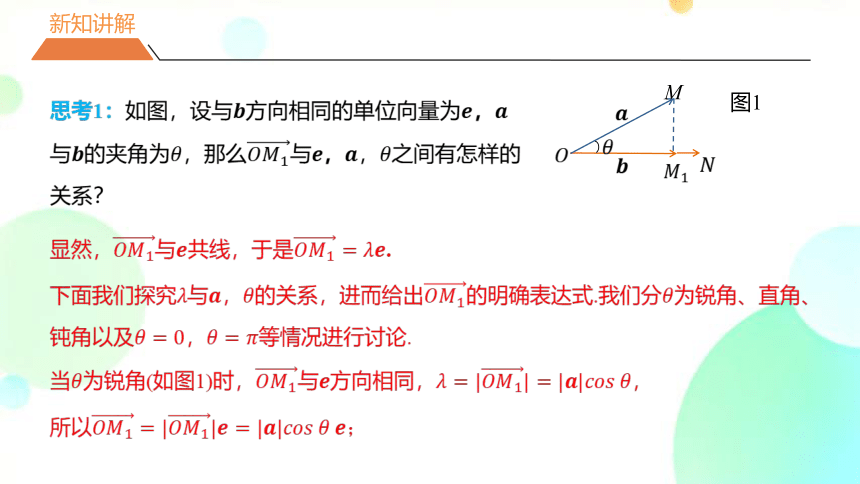
思考1:如图,设与????方向相同的单位向量为????,????与????的夹角为????,那么????????1与????,????,????之间有怎样的关系?
?
????
?
????
?
????
?
????
?
M
????1
?
图1
????
?
显然,????????1与????共线,于是????????1=????????.
下面我们探究????与????,????的关系,进而给出????????1的明确表达式.我们分????为锐角、直角、钝角以及????=0,????=????等情况进行讨论.
当????为锐角(如图1)时,????????1与????方向相同,????=|????????1|=|????|???????????? ????,
所以????????1=|????????1|????=|????|???????????? ???? ????;
?
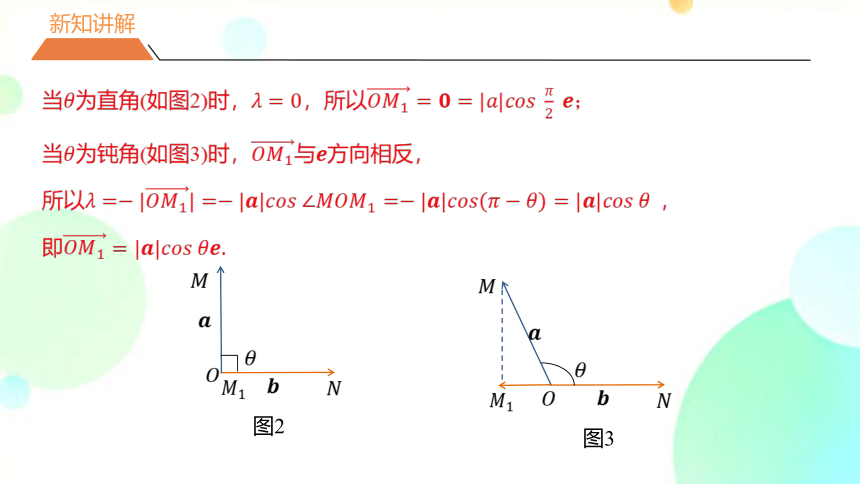
当????为直角(如图2)时,????=0,所以????????1=????=|????|???????????? ????2 ????;
当????为钝角(如图3)时,????????1与????方向相反,
所以????=?|????????1|=?|????|???????????? ∠????????????1=?|????|????????????(?????????)=|????|???????????? ???? ,
即????????1=|????|???????????? ????????.
?
????
?
????
?
????
?
????
?
????
?
????1
?
图2
????
?
????
?
????
?
????
?
????
?
????
?
????1
?
图3
????
?
当????=0时,????=|????|,所以????????1=|????|????=|????|???????????? 0 ????;
当????=????时,????=?|????|,所以????????1=?|????|????=?|????|???????????? ???? ????.
从上面的讨论可知,对于任意的????∈[0,????],都有????????1=|????|???????????? ???? ????.
?
思考2:从上面的探究我们看到,两个非零向量????与????相互平行或垂直时,向量????在向量????上的投影向量具有特殊性.这时,它们的数量积又有怎样的特殊性?
?
由向量数量积的定义,可以得到向量数量积的如下重要性质.
设????,????是非零向量,它们的夹角是????,????是与????方向相同的单位向量,则
(1)?????????=?????????=|????|???????????? ????.
(2)????⊥??????????????=0.
(3)当????与????同向时,?????????=|????||????|;当????与????反向时,?????????=?|????||????|.
特别地,?????????=|????|2或|????|=?????????.
此外,由|???????????? ????|≤1还可以得到
(4)|?????????|≤|????||????|.
?
思考3:如果?????????=0,是否有????=????,或????=?????
不一定,还有可能????=????2.
?
注:?????????常常记作????2.
?
辨析:判断正误.
1.两个向量的数量积是一个向量. ( )
2.向量????在向量????上的投影向量一定与????共线. ( )
3.若?????????<0,则????与????的夹角为钝角. ( )
4.若????≠????,则对任一非零向量????都有?????????≠0. ( )
?
×
×
×
√
题型一:向量数量积的基本计算
例1.已知|????|=6,|????|=5,分别根据下列条件计算????与????的数量积:
(1)????//????;(2)????⊥????;(3)????与????的夹角为60°.
?
解:设????与????的夹角为????.
(1)当????//????时,若????与????同向,则????=0,?????????=|????||????|???????????? 0=6×5=30;
若????与????反向,则????=180°,?????????=|????||????|???????????? 180°=6×5×(?1)=?30.
(2)当????⊥????时,????与????的夹角为90°,?????????=|????||????|???????????? 90°=0.
(3)当????与????的夹角为60°时,?????????=|????||????|???????????? 60°=6×5×12=15.
?
1.已知正三角形????????????的边长为1,求:
(1)?????????????????;(2)?????????????????;(3)?????????????????.
?
解:(1)∵????????与????????的夹角为60°,
∴?????????????????=|????????||????????|???????????? 60°=1×1×12=12.
(2)∵????????与????????的夹角为120°,
∴?????????????????=|????????||????????|???????????? 120°=1×1×(?12)=?12.
(3)∵????????与????????的夹角为60°,
∴?????????????????=|????????||????????|???????????? 60°=1×1×12=12.
?
方法技巧:
利用定义法求平面向量的数量积,关键是找到两向量的模以及夹角,直接利用公式?????????=|????||????|???????????? ????求解.
?
题型二:投影向量的计算
例2.在等腰三角形????????????中,????????=????????=2,∠????????????=30°,????为????????的中点.
(1)求????????在????????上的投影向量;(2)求????????在????????上的投影向量的长度.
?
解:如图,连接????????.因为?????????????为等腰三角形,且????为????????的中点,所以????????⊥????????.
又????????=2,∠????????????=30°,所以????????=????????=????????×???????????? 30°=3.
由图可知????????与????????的夹角为∠????????????的补角,
所以????????与????????的夹角为150°.
(1)????????在????????上的投影向量为|????????|???????????? 150°?????????|????????|=2×(?32)×????????3=?????????.
(2)????????在????????上的投影向量为|????????||???????????? 150°|=3×32=32.
?
????
?
????
?
????
?
????
?
解:由已知得向量????在向量????上的投影向量的模为|????|???????????? 45°=3× 22= 322 .
?
2.已知|????|=3,|????|=5,????与????的夹角为45°,则向量????在向量????上的投影向量的模为( ).
A. 322 B.3 C.4 D.5
?
A
投影向量的求解策略
求投影向量要搞清楚是求哪一个向量在哪一个向量上的投影向量,在正确理解其定义的同时,找准两向量之间的夹角是关键,确定两向量的夹角时,一定要注意“共起点”.
题型三:平面向量的夹角
例3.已知|????|=|????|=2,且????与????的夹角为60°,则????+????与????的夹角是多少??????????与????的夹角又是多少?
?
解:如图所示,作????????=????,????????=????,且∠????????????=60°.
以????????,????????为邻边作平行四边形????????????????,则????????=????+????,????????=?????????.
因为|????|=|????|=2,所以平行四边形????????????????是菱形,
又∠????????????=60°,
所以????????与????????的夹角为30°,????????与????????的夹角为60°,
即????+????与????的夹角是30°,?????????与????的夹角是60°.
?
????
?
????
?
????
?
????
?
????
?
????
?
3.在?????????????中,∠????=90°,????????=12????????,则????????与????????的夹角是( ).
A.30° B.60° C.120° D.150°
?
解:如图,作向量????????=????????,则∠????????????是????????与????????的夹角,在?????????????中,因为∠????????????=90°,????????=12????????,所以∠????????????=60°,所以∠????????????=120°,即????????与????????的夹角是120°.
?
A
?
D
?
C
?
B
?
C
(1)求两个向量的夹角的关键是利用平移的方法使两个向量的起点重合,作两个向量的夹角,按照“一作二证三算”的步骤求出.
(2)特别地,????与????的夹角为????,????1????与????2????(????1,????2是非零常数)的夹角为????0,当????1????2<0时,????0=180°?????;当????1????2>0时,????0=????.
?
向量的夹角
(1)定义:已知两个非零向量????,????(如图),????是平面上的任意一点,作????????=????,????????=????,则∠????????????=????(0≤????≤????)叫做向量????与????的夹角.
(2)当????=0时,????与????同向;当????=????时,????与????反向.
如果????与????的夹角是????2,我们说????与????垂直,记作????⊥????.
?
向量的数量积及其几何意义
(1)定义:已知两个非零向量????与????,它们的夹角为????,我们把数量|????||????|????????????????叫做向量????与????的数量积(或内积),记作?????????,即?????????=|????||????|????????????????.
规定:零向量与任一向量的数量积为0.
(2)投影:设????,????是两个非零向量,????????=????,????????=????,我们考虑如下的变换:过????????的起点????和终点????,分别作????????所在直线的垂线,垂足分别为????1,????1,得到????1????1,我们称上述变换为向量????向向量????投影,????1????1叫做向量????在向量????上的投影向量.
?
????
?
????1
?
????
?
????
?
????
?
????1
?
????
?
????
?
向量数量积的性质
设????,????是非零向量,它们的夹角是????,????是与????方向相同的单位向量,则
(1)?????????=?????????=|????|???????????? ????.
(2)????⊥??????????????=0.
(3)当????与????同向时,?????????=|????||????|;当????与????反向时,?????????=?|????||????|.
特别地,?????????=|????|2或|????|=?????????.
此外,由|???????????? ????|≤1还可以得到
(4)|?????????|≤|????||????|.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
