高一下数学人教A版2019必修第二册 6.4.3 课时3 余弦定理、正弦定理应用举例(共27张PPT)
文档属性
| 名称 | 高一下数学人教A版2019必修第二册 6.4.3 课时3 余弦定理、正弦定理应用举例(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 17:18:42 | ||
图片预览






文档简介
(共27张PPT)
6.4.3 课时3 余弦定理、正弦定理应用举例
会用正弦定理、余弦定理解决生产实践中有关距离、高度、角度的测量问题.
在实践中,我们经常会遇到测量距离、高度、角度等实际问题.解决这类问题,通常需要借助经纬仪以及卷尺等测量角和距离的工具进行测量.
具体测量时,我们常常遇到“不能到达”的困难,这就需要设计恰当的测量方案.下面我们通过几道例题来说明这种情况.需要注意的是,题中为什么要给出这些已知条件,而不是其他的条件.事实上,这些条件往往隐含着相应测量问题在某种特定情境和条件限制下的一个测量方案,而且是这种情境与条件限制下的恰当方案.
辨析:判断正误.
(1)东北方向就是北偏东45的方向.( )
(2)从处望处的仰角为, 从处望处的俯角为,则,的关系为 ( )
(3)俯角是铅垂线与视线所成的角,其范围为. ( )
(4)方位角与方向角其实质是一样的,均是确定观察点与目标点之间的位置关系.( )
√
×
×
√
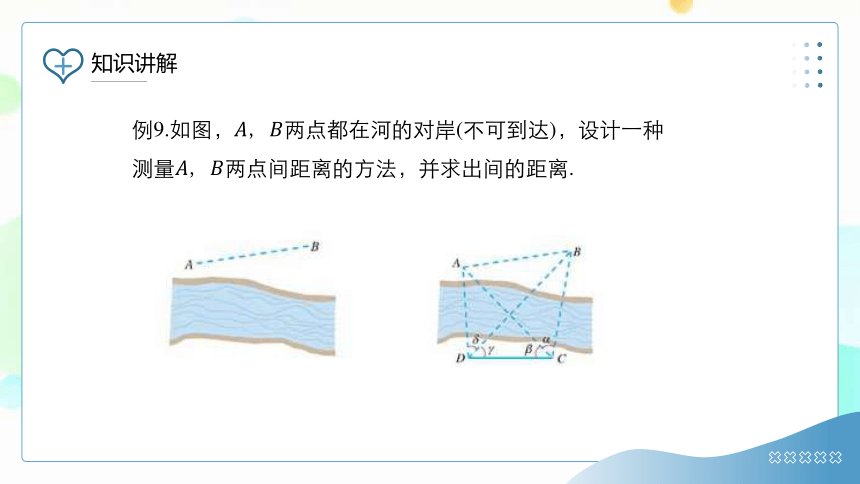
例9.如图,两点都在河的对岸(不可到达),设计一种测量两点间距离的方法,并求出间的距离.
解:如图,在两点的对岸选定两点,测得,并且在两点分别测得,,,.
在和中,由正弦定理,得
于是,在中,由余弦定理可得两点间的距离
思考1:在上述测量方案下,还有其他计算两点间距离的方法吗?
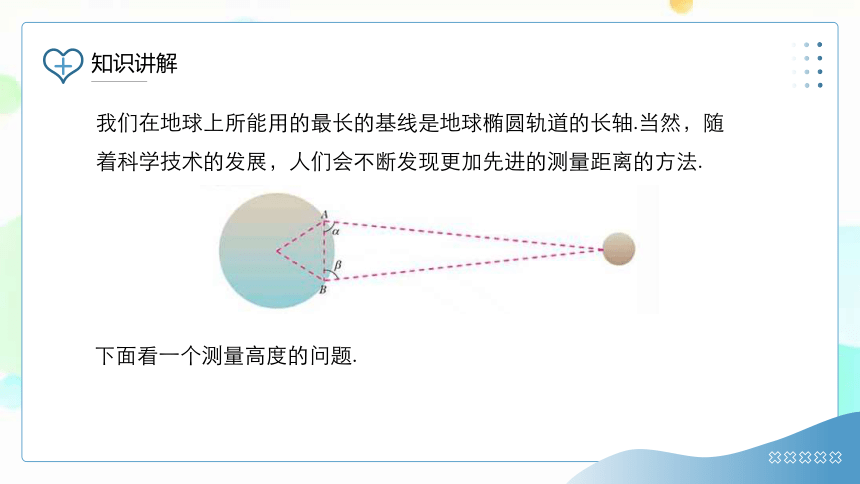
在测量过程中,我们把根据测量的需要而确定的线段叫做基线,如例9中的.为使测量具有较高的精确度,应根据实际需要选取合适的基线长度.一般来说,基线越长,测量的精确度越高.如图,早在1752年,两位法国天文学家为了测量地球与月球之间的距离,利用几乎位于同一经线上的柏林(点)与好望角(点)为基底,测量出的大小,并计算出两地之间的距离,进而算出了地球与月球之间的距离约为.
我们在地球上所能用的最长的基线是地球椭圆轨道的长轴.当然,随着科学技术的发展,人们会不断发现更加先进的测量距离的方法.
下面看一个测量高度的问题.
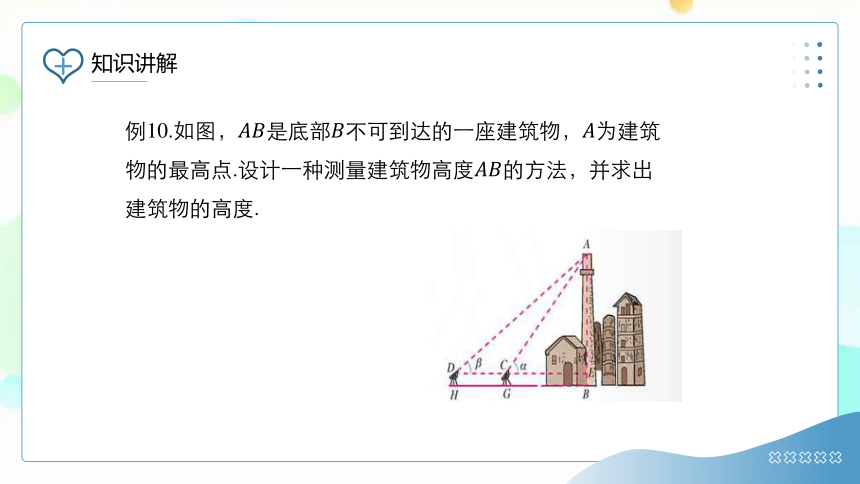
例10.如图,是底部不可到达的一座建筑物,为建筑物的最高点.设计一种测量建筑物高度的方法,并求出建筑物的高度.
解:如图,选择一条水平基线,使三点在同一条直线上.在两点用测角仪器测得的仰角分别是,,,测角仪器的高是.那么,在中,由正弦定理,得
所以,这座建筑物的高度为
例11.位于某海域处的甲船获悉,在其正东方向相距的处有一艘渔船遇险后抛锚等待营救.甲船立即前往救援,同时把消息告知位于甲船南偏西30°,且与甲船相距的处的乙船.那么乙船前往营救遇险渔船时的目标方向线(由观测点看目标的视线)的方向是北偏东多少度(精确到1°)?需要航行的距离是多少海里(精确到1 )?
解:根据题意,画出示意图.由余弦定理,得
于是,.
由正弦定理,得:于是,
由于,所以.
因此,乙船前往营救遇险渔船时的方向约是北偏东,大约需要航行.
题型一:测量距离问题
1.如图,两点都在河的对岸(不可到达).若在河岸选取相距20米的两点,测得,,,那么此时两点间的距离是多少?
解:由正弦定理得:
米),
米).
在中,由余弦定理得,
.
∴两点间的距离是.
1.解决测量具体问题的策略
(1)测量从一个可到达的点到一个不可到达的点之间的距离问题,一般可转化为已知两个角和一条边解三角形的问题,从而运用正弦定理去解决.
(2)测量两个不可到达的点之间的距离问题,一般先把球距离问题转化为运用余弦定理,求三角形的边长的问题,然后把球未知的边长问题转化为只有一点不能到达的两点之间距离的测量问题,最后运用正弦定理解决.
2.解决距离问题的注意点
(1)选定或构造的三角形,要确定及确定在哪一个三角形中求解.
(2)当角边对应,且角的条件较多时,一般用正弦定理;当角的条件较少,且角边不对应时,一般用余弦定理.
题型二:测量高度问题
2.如图所示,是水平面上的两个点,相距800,在点测得山顶的仰角为45°,,又在点测得,其中点是点到水平面的垂足,求山高两.
解:因为,,所以.
因此只需在中求出即可,在中,
,由,
得().
即山的高度为米.
测量高度问题的解题策略
(1)“空间”向“平面”的转化:测量高度问题往往是空间中的问题,因此先要选好所求线段所在的平面,将空间问题转化为平面问题.
(2)“解直角三角形”与“解斜三角形”结合,全面分析所有三角形,仔细规划解题思路.
题型三:测量角度问题
3.“一带一路”国际合作高峰论坛于2017年5月14日至15日在北京举行,会议期间达成了多项国际合作协议,其中有一项是在某国投资建设一个深水港码头,如图,工程师为了了解深水港码头海域海底的构造,在海平面内一条直线上的三点进行测量.已知,,于处测得水深,于处测得水深,于处测得水深,则.
解:如图所示,作交于,交于,作交于.由题中所给数据得
,
,
.
3.“一带一路”国际合作高峰论坛于2017年5月14日至15日在北京举行,会议期间达成了多项国际合作协议,其中有一项是在某国投资建设一个深水港码头,如图,工程师为了了解深水港码头海域海底的构造,在海平面内一条直线上的三点进行测量.已知,,于处测得水深,于处测得水深,于处测得水深,则.
解:在中,由余弦定理的推论,
得.
(1)测量角度与追击问题主要是指在海上、空中或陆地进行测量或计算角度,确定目标的方位,观察某一物体的视角等问题.
(2)解决它们的关键是根据题意和图形以及相关概念,确定所求的角或距离在哪个三角形中,该三角形中已知哪些量,需要求哪些量.通常是根据题意,从实际问题中抽象出一个或几个三角形,然后通过解这些三角形,得到所求的量,从而得到实际问题的解.
实际测量中的有关名称、术语
(1)方位角:从正北方向顺时针转到目标方向线的角.如图所示的,,即表示点A和点B的方位角.故方位角的范围是
实际测量中的有关名称、术语
(2)方向角:指以观测者为中心,正北或正南的方向线与目标方向线所成的小于的水平角,它是方位角的另一种表示形式.如图,图1中表示北偏东,图2中表示南偏西.
实际测量中的有关名称、术语
(3)仰角和俯角与目标视线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线上方时叫做仰角,目标视线在水平视线下方时叫做俯角,如图所示.
(4)视角:观测者的两条视线之间的夹角叫做视角.
6.4.3 课时3 余弦定理、正弦定理应用举例
会用正弦定理、余弦定理解决生产实践中有关距离、高度、角度的测量问题.
在实践中,我们经常会遇到测量距离、高度、角度等实际问题.解决这类问题,通常需要借助经纬仪以及卷尺等测量角和距离的工具进行测量.
具体测量时,我们常常遇到“不能到达”的困难,这就需要设计恰当的测量方案.下面我们通过几道例题来说明这种情况.需要注意的是,题中为什么要给出这些已知条件,而不是其他的条件.事实上,这些条件往往隐含着相应测量问题在某种特定情境和条件限制下的一个测量方案,而且是这种情境与条件限制下的恰当方案.
辨析:判断正误.
(1)东北方向就是北偏东45的方向.( )
(2)从处望处的仰角为, 从处望处的俯角为,则,的关系为 ( )
(3)俯角是铅垂线与视线所成的角,其范围为. ( )
(4)方位角与方向角其实质是一样的,均是确定观察点与目标点之间的位置关系.( )
√
×
×
√
例9.如图,两点都在河的对岸(不可到达),设计一种测量两点间距离的方法,并求出间的距离.
解:如图,在两点的对岸选定两点,测得,并且在两点分别测得,,,.
在和中,由正弦定理,得
于是,在中,由余弦定理可得两点间的距离
思考1:在上述测量方案下,还有其他计算两点间距离的方法吗?
在测量过程中,我们把根据测量的需要而确定的线段叫做基线,如例9中的.为使测量具有较高的精确度,应根据实际需要选取合适的基线长度.一般来说,基线越长,测量的精确度越高.如图,早在1752年,两位法国天文学家为了测量地球与月球之间的距离,利用几乎位于同一经线上的柏林(点)与好望角(点)为基底,测量出的大小,并计算出两地之间的距离,进而算出了地球与月球之间的距离约为.
我们在地球上所能用的最长的基线是地球椭圆轨道的长轴.当然,随着科学技术的发展,人们会不断发现更加先进的测量距离的方法.
下面看一个测量高度的问题.
例10.如图,是底部不可到达的一座建筑物,为建筑物的最高点.设计一种测量建筑物高度的方法,并求出建筑物的高度.
解:如图,选择一条水平基线,使三点在同一条直线上.在两点用测角仪器测得的仰角分别是,,,测角仪器的高是.那么,在中,由正弦定理,得
所以,这座建筑物的高度为
例11.位于某海域处的甲船获悉,在其正东方向相距的处有一艘渔船遇险后抛锚等待营救.甲船立即前往救援,同时把消息告知位于甲船南偏西30°,且与甲船相距的处的乙船.那么乙船前往营救遇险渔船时的目标方向线(由观测点看目标的视线)的方向是北偏东多少度(精确到1°)?需要航行的距离是多少海里(精确到1 )?
解:根据题意,画出示意图.由余弦定理,得
于是,.
由正弦定理,得:于是,
由于,所以.
因此,乙船前往营救遇险渔船时的方向约是北偏东,大约需要航行.
题型一:测量距离问题
1.如图,两点都在河的对岸(不可到达).若在河岸选取相距20米的两点,测得,,,那么此时两点间的距离是多少?
解:由正弦定理得:
米),
米).
在中,由余弦定理得,
.
∴两点间的距离是.
1.解决测量具体问题的策略
(1)测量从一个可到达的点到一个不可到达的点之间的距离问题,一般可转化为已知两个角和一条边解三角形的问题,从而运用正弦定理去解决.
(2)测量两个不可到达的点之间的距离问题,一般先把球距离问题转化为运用余弦定理,求三角形的边长的问题,然后把球未知的边长问题转化为只有一点不能到达的两点之间距离的测量问题,最后运用正弦定理解决.
2.解决距离问题的注意点
(1)选定或构造的三角形,要确定及确定在哪一个三角形中求解.
(2)当角边对应,且角的条件较多时,一般用正弦定理;当角的条件较少,且角边不对应时,一般用余弦定理.
题型二:测量高度问题
2.如图所示,是水平面上的两个点,相距800,在点测得山顶的仰角为45°,,又在点测得,其中点是点到水平面的垂足,求山高两.
解:因为,,所以.
因此只需在中求出即可,在中,
,由,
得().
即山的高度为米.
测量高度问题的解题策略
(1)“空间”向“平面”的转化:测量高度问题往往是空间中的问题,因此先要选好所求线段所在的平面,将空间问题转化为平面问题.
(2)“解直角三角形”与“解斜三角形”结合,全面分析所有三角形,仔细规划解题思路.
题型三:测量角度问题
3.“一带一路”国际合作高峰论坛于2017年5月14日至15日在北京举行,会议期间达成了多项国际合作协议,其中有一项是在某国投资建设一个深水港码头,如图,工程师为了了解深水港码头海域海底的构造,在海平面内一条直线上的三点进行测量.已知,,于处测得水深,于处测得水深,于处测得水深,则.
解:如图所示,作交于,交于,作交于.由题中所给数据得
,
,
.
3.“一带一路”国际合作高峰论坛于2017年5月14日至15日在北京举行,会议期间达成了多项国际合作协议,其中有一项是在某国投资建设一个深水港码头,如图,工程师为了了解深水港码头海域海底的构造,在海平面内一条直线上的三点进行测量.已知,,于处测得水深,于处测得水深,于处测得水深,则.
解:在中,由余弦定理的推论,
得.
(1)测量角度与追击问题主要是指在海上、空中或陆地进行测量或计算角度,确定目标的方位,观察某一物体的视角等问题.
(2)解决它们的关键是根据题意和图形以及相关概念,确定所求的角或距离在哪个三角形中,该三角形中已知哪些量,需要求哪些量.通常是根据题意,从实际问题中抽象出一个或几个三角形,然后通过解这些三角形,得到所求的量,从而得到实际问题的解.
实际测量中的有关名称、术语
(1)方位角:从正北方向顺时针转到目标方向线的角.如图所示的,,即表示点A和点B的方位角.故方位角的范围是
实际测量中的有关名称、术语
(2)方向角:指以观测者为中心,正北或正南的方向线与目标方向线所成的小于的水平角,它是方位角的另一种表示形式.如图,图1中表示北偏东,图2中表示南偏西.
实际测量中的有关名称、术语
(3)仰角和俯角与目标视线在同一铅垂平面内的水平视线和目标视线的夹角,目标视线在水平视线上方时叫做仰角,目标视线在水平视线下方时叫做俯角,如图所示.
(4)视角:观测者的两条视线之间的夹角叫做视角.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
