高一下数学人教A版2019必修第二册 7.1 课时2 复数的几何意义(共20张PPT)
文档属性
| 名称 | 高一下数学人教A版2019必修第二册 7.1 课时2 复数的几何意义(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 386.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
7.1 课时2 复数的几何意义
1.理解复数的几何意义;
2.掌握复平面的实轴、虚轴的概念;
3.理解复数的模,共轭复数的概念,并会用与求解相关问题.
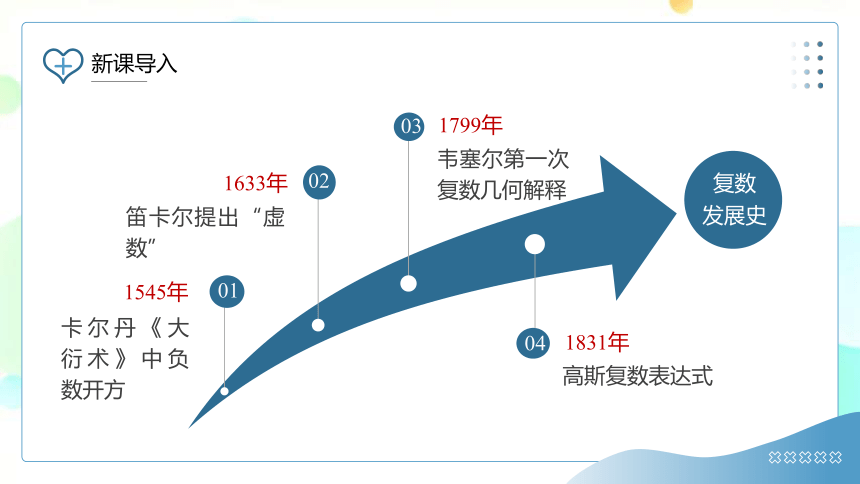
1545年
卡尔丹《大衍术》中负数开方
1633年
笛卡尔提出“虚数”
1799年
韦塞尔第一次复数几何解释
1831年
高斯复数表达式
01
02
03
04
复数
发展史
已知
未知
实数
复数
问题:实数的几何意义?
实数
数轴上的点
(形)
(数)
一一对应
实数a的绝对值
A到原点O的距离
一一对应
问题:复数的一般形式是什么?
复数相等的充要条件是什么?
z=a+bi(a, b∈R)
实部
虚部
实部和虚部分别相等时,复数相等
复数z=a+bi
有序实数对(a,b)
直角坐标系中的点Z(a,b)
(数)
(形)
一一对应
如z=3-2i (3,-2)
x
y
o
b
a
Z(a,b)
一一对应
一一对应
建立了平面直角坐标系来表示复数的平面
x轴------实轴
y轴------虚轴
------复平面
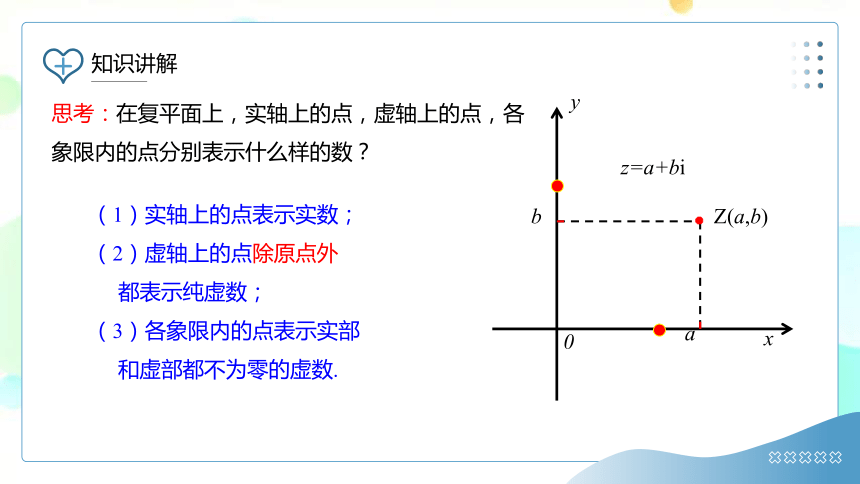
思考:在复平面上,实轴上的点,虚轴上的点,各象限内的点分别表示什么样的数?
x
y
0
Z(a,b)
a
b
z=a+bi
(1)实轴上的点表示实数;
(2)虚轴上的点除原点外
都表示纯虚数;
(3)各象限内的点表示实部
和虚部都不为零的虚数.
复数z=a+bi
复平面内的点Z(a,b)
一一对应
复数的几何意义
口答:在复平面上,下列各点对应哪个复数?
(1)原点(0,0)表示 ;
(2)实轴上的点(2,0)表示 ;
(3)虚轴上的点(0,-1)表示 ;
(4)点(-2,3)表示 .
实数0
实数2
纯虚数-i
复数-2+3i
例1 已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m的取值范围.
表示复数的点所在象限的问题
复数的实部与虚部所满足的不等式组的问题
转化
(几何问题)
(代数问题)
一种重要的数学思想:数形结合思想
变式1:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于直线y=2x+4,求实数m允许的取值范围.
解:∵复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点是(m2+m-6,m2+m-2),
∴(m2+m-2) =2(m2+m-6)+4,
∴m=3或m=-2
x
y
O
Z:a+bi
a
b
复数z=a+bi
平面向量
一一对应
这是复数的另一种几何意义.
为方便起见,常把复数z=a+bi说成点Z或说成向量OZ,并且规定,相等的向量表示同一个复数.
x
y
O
Z(a,b)
a
b
z=a+bi
复数的模
当b=0时,复数z=a+bi是一个实数a,
它的模等于|a|(a的绝对值).
|z|=|a+bi|
复数 z=a+bi的模就是复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离.
复数模的几何意义:
例2 设复数
(1)在复平面内画出复数对应的点和向量;
(2)求复数的模,并比较它们的大小.
例3 设,在复平面内的点为,那么满足下列条件的点的集合是什么图形?
(1)
D
A
复数z=a+bi
平面向量
复平面内的点Z(a,b)
一一对应
一一对应
一一对应
1.复数的几何意义:
2.复数的模:
3.共轭复数:
类比
数形结合
7.1 课时2 复数的几何意义
1.理解复数的几何意义;
2.掌握复平面的实轴、虚轴的概念;
3.理解复数的模,共轭复数的概念,并会用与求解相关问题.
1545年
卡尔丹《大衍术》中负数开方
1633年
笛卡尔提出“虚数”
1799年
韦塞尔第一次复数几何解释
1831年
高斯复数表达式
01
02
03
04
复数
发展史
已知
未知
实数
复数
问题:实数的几何意义?
实数
数轴上的点
(形)
(数)
一一对应
实数a的绝对值
A到原点O的距离
一一对应
问题:复数的一般形式是什么?
复数相等的充要条件是什么?
z=a+bi(a, b∈R)
实部
虚部
实部和虚部分别相等时,复数相等
复数z=a+bi
有序实数对(a,b)
直角坐标系中的点Z(a,b)
(数)
(形)
一一对应
如z=3-2i (3,-2)
x
y
o
b
a
Z(a,b)
一一对应
一一对应
建立了平面直角坐标系来表示复数的平面
x轴------实轴
y轴------虚轴
------复平面
思考:在复平面上,实轴上的点,虚轴上的点,各象限内的点分别表示什么样的数?
x
y
0
Z(a,b)
a
b
z=a+bi
(1)实轴上的点表示实数;
(2)虚轴上的点除原点外
都表示纯虚数;
(3)各象限内的点表示实部
和虚部都不为零的虚数.
复数z=a+bi
复平面内的点Z(a,b)
一一对应
复数的几何意义
口答:在复平面上,下列各点对应哪个复数?
(1)原点(0,0)表示 ;
(2)实轴上的点(2,0)表示 ;
(3)虚轴上的点(0,-1)表示 ;
(4)点(-2,3)表示 .
实数0
实数2
纯虚数-i
复数-2+3i
例1 已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m的取值范围.
表示复数的点所在象限的问题
复数的实部与虚部所满足的不等式组的问题
转化
(几何问题)
(代数问题)
一种重要的数学思想:数形结合思想
变式1:已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于直线y=2x+4,求实数m允许的取值范围.
解:∵复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点是(m2+m-6,m2+m-2),
∴(m2+m-2) =2(m2+m-6)+4,
∴m=3或m=-2
x
y
O
Z:a+bi
a
b
复数z=a+bi
平面向量
一一对应
这是复数的另一种几何意义.
为方便起见,常把复数z=a+bi说成点Z或说成向量OZ,并且规定,相等的向量表示同一个复数.
x
y
O
Z(a,b)
a
b
z=a+bi
复数的模
当b=0时,复数z=a+bi是一个实数a,
它的模等于|a|(a的绝对值).
|z|=|a+bi|
复数 z=a+bi的模就是复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离.
复数模的几何意义:
例2 设复数
(1)在复平面内画出复数对应的点和向量;
(2)求复数的模,并比较它们的大小.
例3 设,在复平面内的点为,那么满足下列条件的点的集合是什么图形?
(1)
D
A
复数z=a+bi
平面向量
复平面内的点Z(a,b)
一一对应
一一对应
一一对应
1.复数的几何意义:
2.复数的模:
3.共轭复数:
类比
数形结合
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
