2024-2025学年苏教版六年级数学下册期末真题汇编专练01-选择题2(含答案+解析)
文档属性
| 名称 | 2024-2025学年苏教版六年级数学下册期末真题汇编专练01-选择题2(含答案+解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 290.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-26 00:00:00 | ||
图片预览




文档简介
2024-2025学年苏教版六年级数学下册期末真题汇编
专练01-选择题2
一、单选题
1.(2024六下·旌阳期末)下面的信息中,适合用扇形统计图表示的是( )。
A.学校各班的学生人数
B.商店一月到六月营业额增长情况
C.牛奶里各种营养成分所占比例情况
2.(2024六下·肇庆期末)李阿姨打算买一台定价为550元的早餐机,甲商场打八折销售,乙商场每满100元返20元。这两家商场的售价相比,( )。
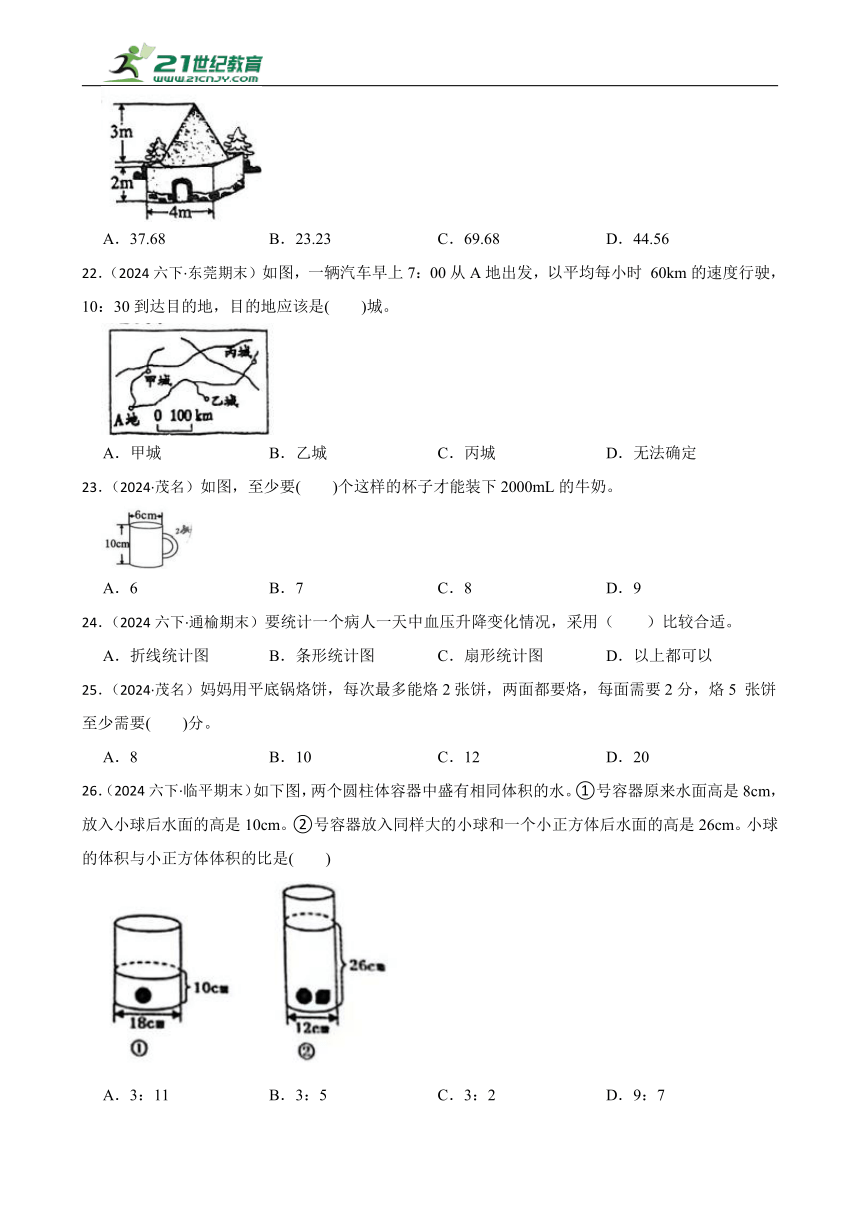
A.乙商场高 B.甲商场高
C.售价相同 D.无法确定哪家高
3.(2024六下·东莞期末)如图所示,下面说法中,正确的是( )。
A.学校在公园南偏东45°方向上 B.公园在学校东偏南45°方向上
C.学校在公园南偏西45°方向上 D.公园在学校西偏南45°方向上
4.(2024六下·黔西南期末)请根据如图提供的信息,寻找圆柱底面直径和高的变化引起侧面积变化的规律,按此规律,第n个圆柱的侧面积是( )。
A. B. C. D.
5.(2024六下·黔西南期末)一根圆柱形木料的底面半径是0.2米,长是4米。如果将它截成4段,这些木料的表面积之和比原木料的表面积增加了( )平方米。
A.0.1256 B.1.248 C.0.5024 D.0.7536
6.(2024六下·黔西南期末)万峰林是中国最大喀斯特峰林之一。在三百六十多年前,著名地理学家徐霞客来到万峰林,发出这样的赞叹:“天下山峰何其多,唯有此处峰成林”。根据小红到万峰林骑行游览路线图,选择下列描述正确的是( )。
A.天坑约在万佛寺北偏西10°方向1.5km处。
B.绿荫塘在万佛寺的东北方。
C.展宏桥约在天坑南偏西55°方向0.6km处。
D.展宏桥在众星捧月的西北方。
7.(2024·茂名)如图,阴影部分的面积是( ) cm2。
A.25.12 B.28.88 C.54 D.50.24
8.(2024六下·黔西南期末)某书店的图书凭优惠卡购买可打八五折,东东用优惠卡买了一本书,省了1.5元。这本书原价( )元钱。
A.10 B.9 C.8 D.11
9.(2024六下·屈原期末)北京市轨道交通6号线全长52.9km,现需要将其画在长60cm、宽20cm的长方形纸上,你认为选哪个比例尺最合适?( )
A.1∶1000 B.1∶10000 C.1∶100000 D.1∶1000000
10.(2024六下·东莞期末)一个圆环形铁片,外圆直径是9cm,内圆直径是5cm,这个圆环形铁片的面积是多少平方厘米?列式正确的是( )。
A.9π-5π B.9π+5π
C.π-π D.π-π
11.(2024六下·通榆期末)小明家在小强家南偏西35°方向上,那么小强家在小明家( )方向上。
A.北偏东35° B.北偏东55° C.东偏南55° D.西偏南55°
12.(2024六下·江阳期末)如果x=2y(x、y均不等于0),那么y∶x=( )。
A.2 B.2∶1 C.1∶2
13.(2024六下·江阳期末)用同样长的铁丝分别围成的长方形、正方形和圆,( )的面积最大。
A.长方形 B.正方形 C.圆
14.(2024六下·衡阳期末)下面选项中,( )最适合绘制折线统计图。
A.要反映培文小学2020~2023年在校学生人数的变化情况。
B.要反映培文小学食堂2024年5月份各种蔬菜用量的情况。
C.要反映培文小学食堂2024年5月份各种蔬菜用量占总用量的百分比情况。
15.(2024六下·衡阳期末)如图,口袋里有3个红球和5个黄球,球除颜色外完全相同,要使摸出红球和黄球的可能性相同,应( )。
A.放入3个红球 B.放入2个红球 C.拿出1个黄球
16.(2024六下·慈利期末)“六一”儿童节,儿童商城一套售价为200元的益智玩具打六折出售,现价比原价便宜( )元。
A.80 B.100 C.120 D.60
17.(2024六下·环江期末)李阿姨买了3000元国家债券,定期3年,年利率是3.14%,到期时利息是( )元.
A.28.26 B.2826 C.282.6 D.3282.6
18.(2024六下·东莞期末)把1m长的圆柱形钢材锯成3段,分成3个小圆柱,表面积增加了120cm2,原来钢材的体积是( )m3。
A.0.3 B.30 C.3000 D.0.003
19.(2024六下·黔西南期末)兴义市万峰林旅游集团旗下景区2023年接待旅游总人数约为385万人次,比上一年增长四成。兴义市万峰林旅游集团旗下景区2022年接待旅游总人数约为( )万人次。
A.154 B.275 C.231 D.95
20.(2024六下·东莞期末)将分别标有数字0,1,2,3,4,5,6的7个相同的小球放在一个不透明的袋子里,从袋子里任意摸出1个球,下面几种情况中发生的可能性最大的是( )
A.球上的数是偶数 B.球上的数是奇数
C.球上的数大于 3 D.球上的数小于3
21.(2024六下·东莞期末)一个圆锥形石顶屋(如图),上面是一个圆锥,下面是一个长方体(长与宽相等),这个石顶屋的体积是( )m3。
A.37.68 B.23.23 C.69.68 D.44.56
22.(2024六下·东莞期末)如图,一辆汽车早上7:00从A地出发,以平均每小时 60km的速度行驶,10:30到达目的地,目的地应该是( )城。
A.甲城 B.乙城 C.丙城 D.无法确定
23.(2024·茂名)如图,至少要( )个这样的杯子才能装下2000mL的牛奶。
A.6 B.7 C.8 D.9
24.(2024六下·通榆期末)要统计一个病人一天中血压升降变化情况,采用( )比较合适。
A.折线统计图 B.条形统计图 C.扇形统计图 D.以上都可以
25.(2024·茂名)妈妈用平底锅烙饼,每次最多能烙2张饼,两面都要烙,每面需要2分,烙5 张饼至少需要( )分。
A.8 B.10 C.12 D.20
26.(2024六下·临平期末)如下图,两个圆柱体容器中盛有相同体积的水。①号容器原来水面高是8cm,放入小球后水面的高是10cm。②号容器放入同样大的小球和一个小正方体后水面的高是26cm。小球的体积与小正方体体积的比是( )
A.3:11 B.3:5 C.3:2 D.9:7
27.(2024六下·临平期末)第一组男生的立定跳远成绩是2.33、2.10、2.82、2.23、2.18、2.82、2.25(单位:米)。用一个数来表示这组同学立定跳远的总体水平,合适的数是( )
A.2.82 B.2.39 C.2.25 D.2.10
28.(2024六下·慈利期末)张阿姨买了一个圆柱形透明玩具收纳桶(如图),这个收纳桶的侧面积是11304,这个收纳桶的底面周长是( )cm。
A.9420 B.706.5 C.2826 D.94.2
29.(2024六下·沅江期末)把一个底面半径是5厘米的圆锥,完全浸没在一个底面直径是20厘米的圆柱形水槽中(如右图),取出圆锥后,水面下降了3厘米,这个圆锥高( )厘米。
A.6 B.12 C.36 D.48
30.(2024六下·临平期末)下列数量关系中,成反比例关系的是( )
A.全班人数一定,出勤人数和缺勤人数
B.单价一定,数量和总价
C.运送一批货物,每天运的吨数和需要的天数
D.圆的周长和半径
31.(2024六下·沅江期末)博物馆展出了一个高为19.6厘米的秦代将军俑模型,它的高度与实际高度的比是1∶10。这个将军俑的实际高度是( )米。
A.19.6 B.196 C.1.96 D.0.196
32.(2024六下·瑞安期末)下列关系中表示错误的是( )
A. B.
C. D.
33.(2024六下·温岭期末)甲、乙、丙、丁四位同学练习投垒球,每人投3次结果如图所示。这四位同学中,( )投垒球的平均成绩大约是 28m。
A.甲 B.乙 C.丙 D.丁
34.(2024六下·沅江期末)用下图的转盘做游戏,指针落在红色区域的可能性是( )。
A. B. C. D.
35.(2024六下·邵阳期末)口袋里有2个红球、3个白球和5个黄球,从中任意摸出一个球,摸到( )的可能性最大。
A.红球 B.黄球 C.白球
36.(2024六下·杭州期末)下面各物体中,不能用“底面积×高"求它体积的物体是( )
A. B.
C. D.
37.(2024六下·屈原期末)下列说法中正确的有几个( )。
①一个圆的面积与它的半径的平方成正比例关系。
②当为假分数时(m,n均为非0自然数),一定大于1
③将圆锥沿高切开,切面形状是等腰三角形。
④百分数可以看成后项为100的特殊形式的比。
A.4 B.3 C.2 D.1
38.(2024六下·屈原期末)一盒巧克力饼干的包装盒上标着“净重”的字样,随机抽取5盒这种饼干,测得它们的净重分别为、、、、,本次抽查的合格率为( )。
A. B. C. D.
39.(2024六下·屈原期末)有三个转盘,小龙转动了30次,统计结果如右表所示。小龙最有可能转动的是哪个转盘( )。
□ ○
8次 22次
A. B. C. D.
40.(2024六下·双牌期末)下面适合用扇形统计图表示的是( )。
A.校园内各种树木的数量情况
B.江华县2024年5月气温变化情况
C.各年级人数占全校总人数的百分比
D.浩浩近5年的身高数据
41.(2024六下·双牌期末)下面图形旋转就会形成圆锥。
A. B. C. D.
42.(2024六下·重庆市期末)如图,一个拧紧瓶盖的瓶子里水的体积占瓶子容积的60%,正放时,瓶内水的高度是15cm;倒放以后,水面距离瓶底( )cm
A.10 B.12 C.15 D.25
43.(2024六下·重庆市期末)用四根木条制作一个长方形框架,双手将它的两个对角慢慢向两边拉动,在这个变化过程中,平行四边形的面积和高( )
A.成正比例 B.成反比例 C.不成比例 D.无法确定
44.(2024六下·鹿城期末)如图所示是一个无盖的长方体纸盒,下面说法正确的是( )
A.纸盒的底面积是 300cm2 B.纸盒的棱长总和是90cm
C.纸盒的表面积是550cm2 D.纸盒的容积是750cm3
45.(2024六下·鹿城期末)把一个底面直径 6cm 高 4cm 的圆柱体木块加工成一个等底等高的圆锥。下面说法正确的是( )
A.去掉的体积是圆锥体积的2倍 B.圆锥的底面积是 36πcm2
C.去掉的体积是圆柱体积的 D.圆锥和圆柱体积的比是1:2
46.(2024六下·鹿城期末)下面问题可以用反比例来解决的是( )。
A.中国空间站在太空中绕地球运行6周需要大约需要9小时,运行15周大约要多少时间?
B.某雨水收集处理站2年可提供5万吨冲厕水。照这样计算,5年可提供多少吨冲厕水?
C.25 元一本的书,小明的钱可以买6本。用这些钱买30元一本的书,可以买几本?
D.某枇杷园每天销售 750千克枇杷。如果每千克售价 70元,每天可收入多少元?
47.(2024六下·鹿城期末)小舟在计算如下算式时,算法正确的是( )。
A.1.2×0.08=12×8×(0.1×0.1) B.120÷80=12÷8÷10÷10
C.1.2×20=12×2×10 D.
48.(2024六下·温岭期末)下面说法正确的有( )个。
①男生比女生多 25%,就是女生比男生少
②学校舞蹈队共有 26名队员,至少有3名队员在同一个月过生日。
③y= x,x和y成反比例。
④已知x+2y+1=6,则 3x +6 y +3=18。
A.1 B.2 C.3 D.4
(2024六下·余杭期末)先阅读下面文字材料,再选择正确答案的字母填入括号内。
暑假期间,小明一家开车前往湘湖游玩,从家出发,以40千米/小时的平均速度行驶了 36分钟到达景区。下午,小明一家在金沙滩玩耍,小明盛了大半桶水,把许多小石头放入桶里,溢出了一部分水,然后把洗干净的小石头捞出来。小明用这些小石头等距离地围成了一个正方形的圈(如图),每两颗石头之间的距离是5厘米,正好用了40颗石头。小明继续玩沙子,他用圆锥形漏斗装满沙子,正好倒了两次把圆柱形水桶装满。
49.小明用小石头围成的正方形圈的周长是( )米。
A.205 B.1.95 C.200 D.2
50.小明家到湘湖的路程是( )千米。
A.1440 B.14.4 C.24 D.36
51.小明用小石头围成的正方形圈的面积是( )平方厘米。
A.3025 B.2025 C.3000 D.2500
52.若圆柱形水桶和圆锥形漏斗的底面积一样大,那么圆柱形水桶的高是圆锥形漏斗高的( )。
A. B. C.2倍 D.3倍
53.能正确反映在水桶中放入小石头到捞出小石头的过程中,水桶中水的深度变化情况的是( )。
A. B.
C. D.
54.(2024六下·杭州期末)将一个正方体木块6个面都涂上红色,把它切成大小相等的27块小正方体。两个面涂上红色的小正方体有( )块。
A.8 B.12 C.24 D.48
答案解析部分
1.C
2.A
3.C
4.C
5.D
6.C
7.B
解:(8+10)×6÷2-3.14×÷2=54-25.12= 28.88(平方厘米)
故答案为:B
阴影部分的面积=梯形的面积-圆的面积。梯形的面积=。圆的面积=。(由于选项没有所以将取3.14进行计算。)
8.A
9.C
10.D
11.A
12.C
13.C
14.A
15.B
16.A
17.C
18.D
解:把圆柱形钢材锯成3段,增加了4个底面积,
120÷4=30(平方厘米)
30×100=3000(立方厘米)=0.003(立方米)
原来钢材的体积是0.003立方米
故答案为:D。
增加的表面积÷4=圆柱的底面积,圆柱的底面积×高=圆柱的体积,计算时注意单位的变化。
19.B
20.A
解:7个数字有4个偶数,3个奇数,大于3的数有3个,小于3的数有3个,
下面几种情况中发生的可能性最大的是球上的数是偶数。
故答案为:A。
可能性的大小与它在总数中所占数量的多少有关,在总数中占的数量多,摸到的可能性就大,占的数量小,摸到的可能性就小,占的数量相等,摸到的可能性也相等。
21.D
解:圆锥的底面直径是4米,底面半径是2米,
圆锥的体积:3.14×2×2×3÷3=12.56(立方米)
长方体的体积:4×4×2=32(立方米)
石顶屋的体积:12.56+32=44.56(立方米)
故答案为:D。
圆锥的体积=π×底面半径的平方×高÷3,长方体的体积=长×宽×高,圆锥的体积+长方体的体积=这个石顶屋的体积。
22.B
解:10:30-7:00=3.5小时
60×3.5=210(千米)
210÷100=2.1(厘米)
目的地应该是乙城。
故答案为:B。
行驶的速度×行驶的时间=行驶的路程,行驶的路程÷1厘米代表的长度=图上的长度,据此解答。
23.B
解:=300。7
故答案为:B
先求出杯子的容积:=h==300。牛奶的容积÷杯子的容积=至少需要的杯子数目。
24.A
25.B
解:2×2=4,2×3=6,4+6=10。
故答案为:B
烙2张饼按照正常方法烙,共需要2×2=4(分钟);剩下3张可以这样煎:第一次:放①的正面和②的正面,第二次:放①的反面和③的正面,第三次:放②的反面和③的反面,共用2×3=6(分钟);全部时间:4+6=10(分钟)。
26.D
解:小球的体积:
π×(18÷2)2×(10-8)
=π×81×2
=162π(立方厘米);
小正方体的体积:
π×(12÷2)2×26-π×(18÷2)2×8-162π
=π×36×26-π×81×8-162π
=936π-648π-162π
=126π(立方厘米);
(162π):(126π)=9:7。
故答案为:D。
放入小球后水面增高了,用减法求出增高了几厘米,因为增高的水的体积就是小球的体积,可根据圆柱的体积=πr2h,代入数据计算求出小球的体积;再根据第一个圆柱中原来有的高度是8厘米,及圆柱体的体积=πr2h,代入数据计算求出水的体积;因为两个容器的水的体积相同,再根据第二个圆柱的水的高度,求出总体积,再减去水的体积与小球的体积,即可求出小长方体的体积;最后根据比的意义,用小球的体积比小长方体的体积,然后化简比。
27.B
解:(2.33+2.10+2.82+2.23+2.18+2.82+2.25)÷7
=16.73÷7
=2.39(米)。
故答案为:B。
合适的数是这组数据的平均数,因为平均数能代表一组数据的总体水平。
28.D
29.C
30.C
解:A项:出勤人数+缺勤人数=全班人数,不成比例关系;
B项:总价÷数量=单价(一定), 单价一定,数量和总价成正比例关系;
C项:每天运的吨数×需要的天数=运送货物的总质量(一定),运送一批货物,每天运的吨数和需要的天数成反比例;
D项:圆的周长÷2÷半径=π(一定),圆的周长和半径成正比例。
故答案为:C。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
31.C
32.C
解:A项:三角形按角分为:直角三角形、钝角三角形、锐角三角形,原题干说法正确;
B项:正方形是特殊的长方形,长方形是特殊的平行四边形,原题干说法正确;
C项:垂直是相交的一种,原题干说法错误;
D项:正方体是特殊的长方体,还有圆柱、圆锥都是立体图形,原题干说法正确。
故答案为:C。
正方形是特殊的长方形,正方体是特殊的长方体,垂直是相交的一种情况。
33.B
解:A项:甲平均成绩低于28m;
B项:乙平均成绩大约28m;
C项:丙平均成绩高于28m;
D项:丁平均成绩低于28m。
故答案为:B。
平均数表示一组数据的整体水平,只有乙的成绩一次等于28米,一次成绩低于28米,剩余一次成绩高于28米,则平均成绩大约28米。
34.C
35.B
36.C
解:A、长方体是柱体,可以利用公式求体积;
B、是柱体,可以利用公式求体积;
C、是柱体,但不能用底面积×高计算体积;
D、长方体是柱体,可以利用公式求体积。
故答案为:C。
本题考查柱体的体积的公式,解题的关键是了解柱体的体积通项公式的运用条件。
37.B
38.D
39.B
40.C
41.B
42.A
解:60%÷15=0.04(平方厘米)
(1-60%)÷0.04
=0.4÷0.04
=10(厘米)。
故答案为:A。
把瓶子的容积看作单位"1",把瓶子的容积看作是水的体积和空气的体积之和,因为水的体积占瓶子容积的60%,则空气的体积占瓶子容积的(1-60%),假设瓶子底面积为 S ,瓶子倒放后水面距离瓶底的高度为 h 。则根据题意可得:15S=60%,Sh =40%,据此即可求出h。
43.A
解:在这个变化过程中,平行四边形的面积÷高=底(一定),平行四边形的面积和高成正比例。
故答案为:A。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
44.D
解:A项:15×10=150(平方厘米),原题干说法错误;
B项:(15+10+5)×4
=30×4
=120(厘米),原题干说法错误;
C项:15×10+(15×5+10×5)×2
=150+125×2
=150+250
=400(平方厘米),原题干说法错误;
D项:15×10×5
=150×5
=750(立方厘米),原题干说法正确。
故答案为:D。
A项:纸盒的底面积=长×宽;
B项:纸盒的棱长和=(长+宽+高)×4;
C项:纸盒的表面积=长×宽+(长×高+宽×高)×2;
D项:纸盒的体积=长×宽×高。
45.A
解:A项:去掉的体积是圆锥体积的2倍,原题干说法正确;
B项:π×(6÷2)2=9π,原题干说法错误;
C项:去掉的体积是圆柱体积的2倍,原题干说法错误;
D项:圆锥和圆柱体积的比是1:3,原题干说法错误。
故答案为:A。
圆锥的底面积=π×半径2,等底等高的圆柱的体积是圆锥体积的3倍,据此判断。
46.C
解:A项:运行的时间÷运行的周数=空间站绕地球运行一周的时间(一定),成正比例关系;
B项:冲厕水的总吨数÷年数=每年提供的冲厕水的吨数(一定),成正比例关系;
C项:书的单价 ×数量=小明带的钱数(一定),成反比例关系;
D项:单价=总价÷数量(一定),成正比例关系。
故答案为:C。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
47.D
解:A项:1.2×0.08=12×8×(0.1×0.01) ,原题干计算错误;
B项:120÷80=12÷8÷10 ,原题干计算错误;
C项:1.2×20=1.2×2×10 ,原题干计算错误;
D项:×=(3×6)×(×),原题干计算正确。
故答案为:D。
A项:1.2是一位小数,0.08是两位小数,所以1.2×0.08=12×8×(0.1×0.01) ;
B项:80=8×10,则120÷80=12÷8÷10 ;
C项:20=2×10,所以1.2×20=1.2×2×10 ;
D项:计算×时,可以先把各自计数单位的个数相乘,然后再乘它们分数单位的积。
48.C
解:A项:25%÷125%=20%,原题干说法正确;
B项:26÷12=2(人)······2(人)
2+1=3(人),原题干说法正确;
C项:y= x,则=4(一定),x和y成正比例,原题干说法错误;
D项:x+2y+1=6
3(x+2y+1)=6×3
3x +6 y +3=18,原题干说法正确。
故答案为:C。
A项:把女生人数看作单位“1”,男生人数是1+25%=125%,女生比男生少的分率=25%÷男生人数;
B项:抽屉原理,至少在同一抽屉里相同物体的个数=物体总个数÷抽屉的个数+1;
C项:判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;
D项:等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
49.D
50.C
51.D
52.A
53.D
(1)摆成正方形用的石头数÷4=一边用的石头数,一边用的石头数-1=一边的间隔数,一边的间隔数×1个间隔的长度=正方形的边长,正方形的边长×4=正方形的周长;
(2)计算小明家到湘湖的路程:根据题目,小明一家以40千米/小时的平均速度行驶了36分钟到达景区。首先,需要将36分钟转换为小时,然后,根据路程 = 速度 × 时间,计算路程;
(3)计算正方形圈的面积:已知正方形的周长是200厘米,因为正方形有四条边且每条边长相等,所以每条边长是50厘米,根据正方形的面积是边长的平方求出面积;
(4)分析圆柱形水桶的高与圆锥形漏斗高的关系:小明用圆锥形漏斗装满沙子,正好倒了两次把圆柱形水桶装满。这意味着圆柱形水桶的体积是圆锥形漏斗体积的两倍。由于圆柱形水桶和圆锥形漏斗的底面积一样大,所以我们可以根据圆柱与圆锥的体积公式来分析他们的高度关系;
(5)根据题意可知,起始点在坐标轴上部分,水满后一段时间内水位不变,水位下降后,水位比刚开始低,据此判断。
49.解:40÷4=10(颗)
10-1=9(个)
5×9=45(厘米)
45×4=180(厘米);
故答案为:D。
50.解:(小时),
(千米);
故答案为:C。
51.解:(厘米),
(平方厘米);
故答案为:D。
52.解:圆柱的体积为,圆锥的体积为,
由于 正好倒了两次把圆柱形水桶装满,
则,
简化后得到,
即圆柱形水桶的高是圆锥形漏斗高的;
故答案为:A。
53.解:由于小明盛了大半桶水,则起始点在坐标轴上部分,
把许多小石头放入桶里,溢出了一部分水,则水满后一段时间内水位不变,
把洗干净的小石头捞出,水位开始下降,
由于溢出了一部分水,则水位比刚开始低,
综上,D符合条件;
故答案为:D。
54.B
解:两面涂色的个数:12×(3-2)
=12×1
=12(个)
故答案为:B。
用n表示大正方体每条棱上小正方体的块数,三面涂色的小正方体的块数=8(顶点的个数);两面涂色的小正方体的块数=12×(n-2);一面涂色的小正方体的块数=6×(n-2)2;没有涂色的小正方体的块数=(n-2)3。
专练01-选择题2
一、单选题
1.(2024六下·旌阳期末)下面的信息中,适合用扇形统计图表示的是( )。
A.学校各班的学生人数
B.商店一月到六月营业额增长情况
C.牛奶里各种营养成分所占比例情况
2.(2024六下·肇庆期末)李阿姨打算买一台定价为550元的早餐机,甲商场打八折销售,乙商场每满100元返20元。这两家商场的售价相比,( )。
A.乙商场高 B.甲商场高
C.售价相同 D.无法确定哪家高
3.(2024六下·东莞期末)如图所示,下面说法中,正确的是( )。
A.学校在公园南偏东45°方向上 B.公园在学校东偏南45°方向上
C.学校在公园南偏西45°方向上 D.公园在学校西偏南45°方向上
4.(2024六下·黔西南期末)请根据如图提供的信息,寻找圆柱底面直径和高的变化引起侧面积变化的规律,按此规律,第n个圆柱的侧面积是( )。
A. B. C. D.
5.(2024六下·黔西南期末)一根圆柱形木料的底面半径是0.2米,长是4米。如果将它截成4段,这些木料的表面积之和比原木料的表面积增加了( )平方米。
A.0.1256 B.1.248 C.0.5024 D.0.7536
6.(2024六下·黔西南期末)万峰林是中国最大喀斯特峰林之一。在三百六十多年前,著名地理学家徐霞客来到万峰林,发出这样的赞叹:“天下山峰何其多,唯有此处峰成林”。根据小红到万峰林骑行游览路线图,选择下列描述正确的是( )。
A.天坑约在万佛寺北偏西10°方向1.5km处。
B.绿荫塘在万佛寺的东北方。
C.展宏桥约在天坑南偏西55°方向0.6km处。
D.展宏桥在众星捧月的西北方。
7.(2024·茂名)如图,阴影部分的面积是( ) cm2。
A.25.12 B.28.88 C.54 D.50.24
8.(2024六下·黔西南期末)某书店的图书凭优惠卡购买可打八五折,东东用优惠卡买了一本书,省了1.5元。这本书原价( )元钱。
A.10 B.9 C.8 D.11
9.(2024六下·屈原期末)北京市轨道交通6号线全长52.9km,现需要将其画在长60cm、宽20cm的长方形纸上,你认为选哪个比例尺最合适?( )
A.1∶1000 B.1∶10000 C.1∶100000 D.1∶1000000
10.(2024六下·东莞期末)一个圆环形铁片,外圆直径是9cm,内圆直径是5cm,这个圆环形铁片的面积是多少平方厘米?列式正确的是( )。
A.9π-5π B.9π+5π
C.π-π D.π-π
11.(2024六下·通榆期末)小明家在小强家南偏西35°方向上,那么小强家在小明家( )方向上。
A.北偏东35° B.北偏东55° C.东偏南55° D.西偏南55°
12.(2024六下·江阳期末)如果x=2y(x、y均不等于0),那么y∶x=( )。
A.2 B.2∶1 C.1∶2
13.(2024六下·江阳期末)用同样长的铁丝分别围成的长方形、正方形和圆,( )的面积最大。
A.长方形 B.正方形 C.圆
14.(2024六下·衡阳期末)下面选项中,( )最适合绘制折线统计图。
A.要反映培文小学2020~2023年在校学生人数的变化情况。
B.要反映培文小学食堂2024年5月份各种蔬菜用量的情况。
C.要反映培文小学食堂2024年5月份各种蔬菜用量占总用量的百分比情况。
15.(2024六下·衡阳期末)如图,口袋里有3个红球和5个黄球,球除颜色外完全相同,要使摸出红球和黄球的可能性相同,应( )。
A.放入3个红球 B.放入2个红球 C.拿出1个黄球
16.(2024六下·慈利期末)“六一”儿童节,儿童商城一套售价为200元的益智玩具打六折出售,现价比原价便宜( )元。
A.80 B.100 C.120 D.60
17.(2024六下·环江期末)李阿姨买了3000元国家债券,定期3年,年利率是3.14%,到期时利息是( )元.
A.28.26 B.2826 C.282.6 D.3282.6
18.(2024六下·东莞期末)把1m长的圆柱形钢材锯成3段,分成3个小圆柱,表面积增加了120cm2,原来钢材的体积是( )m3。
A.0.3 B.30 C.3000 D.0.003
19.(2024六下·黔西南期末)兴义市万峰林旅游集团旗下景区2023年接待旅游总人数约为385万人次,比上一年增长四成。兴义市万峰林旅游集团旗下景区2022年接待旅游总人数约为( )万人次。
A.154 B.275 C.231 D.95
20.(2024六下·东莞期末)将分别标有数字0,1,2,3,4,5,6的7个相同的小球放在一个不透明的袋子里,从袋子里任意摸出1个球,下面几种情况中发生的可能性最大的是( )
A.球上的数是偶数 B.球上的数是奇数
C.球上的数大于 3 D.球上的数小于3
21.(2024六下·东莞期末)一个圆锥形石顶屋(如图),上面是一个圆锥,下面是一个长方体(长与宽相等),这个石顶屋的体积是( )m3。
A.37.68 B.23.23 C.69.68 D.44.56
22.(2024六下·东莞期末)如图,一辆汽车早上7:00从A地出发,以平均每小时 60km的速度行驶,10:30到达目的地,目的地应该是( )城。
A.甲城 B.乙城 C.丙城 D.无法确定
23.(2024·茂名)如图,至少要( )个这样的杯子才能装下2000mL的牛奶。
A.6 B.7 C.8 D.9
24.(2024六下·通榆期末)要统计一个病人一天中血压升降变化情况,采用( )比较合适。
A.折线统计图 B.条形统计图 C.扇形统计图 D.以上都可以
25.(2024·茂名)妈妈用平底锅烙饼,每次最多能烙2张饼,两面都要烙,每面需要2分,烙5 张饼至少需要( )分。
A.8 B.10 C.12 D.20
26.(2024六下·临平期末)如下图,两个圆柱体容器中盛有相同体积的水。①号容器原来水面高是8cm,放入小球后水面的高是10cm。②号容器放入同样大的小球和一个小正方体后水面的高是26cm。小球的体积与小正方体体积的比是( )
A.3:11 B.3:5 C.3:2 D.9:7
27.(2024六下·临平期末)第一组男生的立定跳远成绩是2.33、2.10、2.82、2.23、2.18、2.82、2.25(单位:米)。用一个数来表示这组同学立定跳远的总体水平,合适的数是( )
A.2.82 B.2.39 C.2.25 D.2.10
28.(2024六下·慈利期末)张阿姨买了一个圆柱形透明玩具收纳桶(如图),这个收纳桶的侧面积是11304,这个收纳桶的底面周长是( )cm。
A.9420 B.706.5 C.2826 D.94.2
29.(2024六下·沅江期末)把一个底面半径是5厘米的圆锥,完全浸没在一个底面直径是20厘米的圆柱形水槽中(如右图),取出圆锥后,水面下降了3厘米,这个圆锥高( )厘米。
A.6 B.12 C.36 D.48
30.(2024六下·临平期末)下列数量关系中,成反比例关系的是( )
A.全班人数一定,出勤人数和缺勤人数
B.单价一定,数量和总价
C.运送一批货物,每天运的吨数和需要的天数
D.圆的周长和半径
31.(2024六下·沅江期末)博物馆展出了一个高为19.6厘米的秦代将军俑模型,它的高度与实际高度的比是1∶10。这个将军俑的实际高度是( )米。
A.19.6 B.196 C.1.96 D.0.196
32.(2024六下·瑞安期末)下列关系中表示错误的是( )
A. B.
C. D.
33.(2024六下·温岭期末)甲、乙、丙、丁四位同学练习投垒球,每人投3次结果如图所示。这四位同学中,( )投垒球的平均成绩大约是 28m。
A.甲 B.乙 C.丙 D.丁
34.(2024六下·沅江期末)用下图的转盘做游戏,指针落在红色区域的可能性是( )。
A. B. C. D.
35.(2024六下·邵阳期末)口袋里有2个红球、3个白球和5个黄球,从中任意摸出一个球,摸到( )的可能性最大。
A.红球 B.黄球 C.白球
36.(2024六下·杭州期末)下面各物体中,不能用“底面积×高"求它体积的物体是( )
A. B.
C. D.
37.(2024六下·屈原期末)下列说法中正确的有几个( )。
①一个圆的面积与它的半径的平方成正比例关系。
②当为假分数时(m,n均为非0自然数),一定大于1
③将圆锥沿高切开,切面形状是等腰三角形。
④百分数可以看成后项为100的特殊形式的比。
A.4 B.3 C.2 D.1
38.(2024六下·屈原期末)一盒巧克力饼干的包装盒上标着“净重”的字样,随机抽取5盒这种饼干,测得它们的净重分别为、、、、,本次抽查的合格率为( )。
A. B. C. D.
39.(2024六下·屈原期末)有三个转盘,小龙转动了30次,统计结果如右表所示。小龙最有可能转动的是哪个转盘( )。
□ ○
8次 22次
A. B. C. D.
40.(2024六下·双牌期末)下面适合用扇形统计图表示的是( )。
A.校园内各种树木的数量情况
B.江华县2024年5月气温变化情况
C.各年级人数占全校总人数的百分比
D.浩浩近5年的身高数据
41.(2024六下·双牌期末)下面图形旋转就会形成圆锥。
A. B. C. D.
42.(2024六下·重庆市期末)如图,一个拧紧瓶盖的瓶子里水的体积占瓶子容积的60%,正放时,瓶内水的高度是15cm;倒放以后,水面距离瓶底( )cm
A.10 B.12 C.15 D.25
43.(2024六下·重庆市期末)用四根木条制作一个长方形框架,双手将它的两个对角慢慢向两边拉动,在这个变化过程中,平行四边形的面积和高( )
A.成正比例 B.成反比例 C.不成比例 D.无法确定
44.(2024六下·鹿城期末)如图所示是一个无盖的长方体纸盒,下面说法正确的是( )
A.纸盒的底面积是 300cm2 B.纸盒的棱长总和是90cm
C.纸盒的表面积是550cm2 D.纸盒的容积是750cm3
45.(2024六下·鹿城期末)把一个底面直径 6cm 高 4cm 的圆柱体木块加工成一个等底等高的圆锥。下面说法正确的是( )
A.去掉的体积是圆锥体积的2倍 B.圆锥的底面积是 36πcm2
C.去掉的体积是圆柱体积的 D.圆锥和圆柱体积的比是1:2
46.(2024六下·鹿城期末)下面问题可以用反比例来解决的是( )。
A.中国空间站在太空中绕地球运行6周需要大约需要9小时,运行15周大约要多少时间?
B.某雨水收集处理站2年可提供5万吨冲厕水。照这样计算,5年可提供多少吨冲厕水?
C.25 元一本的书,小明的钱可以买6本。用这些钱买30元一本的书,可以买几本?
D.某枇杷园每天销售 750千克枇杷。如果每千克售价 70元,每天可收入多少元?
47.(2024六下·鹿城期末)小舟在计算如下算式时,算法正确的是( )。
A.1.2×0.08=12×8×(0.1×0.1) B.120÷80=12÷8÷10÷10
C.1.2×20=12×2×10 D.
48.(2024六下·温岭期末)下面说法正确的有( )个。
①男生比女生多 25%,就是女生比男生少
②学校舞蹈队共有 26名队员,至少有3名队员在同一个月过生日。
③y= x,x和y成反比例。
④已知x+2y+1=6,则 3x +6 y +3=18。
A.1 B.2 C.3 D.4
(2024六下·余杭期末)先阅读下面文字材料,再选择正确答案的字母填入括号内。
暑假期间,小明一家开车前往湘湖游玩,从家出发,以40千米/小时的平均速度行驶了 36分钟到达景区。下午,小明一家在金沙滩玩耍,小明盛了大半桶水,把许多小石头放入桶里,溢出了一部分水,然后把洗干净的小石头捞出来。小明用这些小石头等距离地围成了一个正方形的圈(如图),每两颗石头之间的距离是5厘米,正好用了40颗石头。小明继续玩沙子,他用圆锥形漏斗装满沙子,正好倒了两次把圆柱形水桶装满。
49.小明用小石头围成的正方形圈的周长是( )米。
A.205 B.1.95 C.200 D.2
50.小明家到湘湖的路程是( )千米。
A.1440 B.14.4 C.24 D.36
51.小明用小石头围成的正方形圈的面积是( )平方厘米。
A.3025 B.2025 C.3000 D.2500
52.若圆柱形水桶和圆锥形漏斗的底面积一样大,那么圆柱形水桶的高是圆锥形漏斗高的( )。
A. B. C.2倍 D.3倍
53.能正确反映在水桶中放入小石头到捞出小石头的过程中,水桶中水的深度变化情况的是( )。
A. B.
C. D.
54.(2024六下·杭州期末)将一个正方体木块6个面都涂上红色,把它切成大小相等的27块小正方体。两个面涂上红色的小正方体有( )块。
A.8 B.12 C.24 D.48
答案解析部分
1.C
2.A
3.C
4.C
5.D
6.C
7.B
解:(8+10)×6÷2-3.14×÷2=54-25.12= 28.88(平方厘米)
故答案为:B
阴影部分的面积=梯形的面积-圆的面积。梯形的面积=。圆的面积=。(由于选项没有所以将取3.14进行计算。)
8.A
9.C
10.D
11.A
12.C
13.C
14.A
15.B
16.A
17.C
18.D
解:把圆柱形钢材锯成3段,增加了4个底面积,
120÷4=30(平方厘米)
30×100=3000(立方厘米)=0.003(立方米)
原来钢材的体积是0.003立方米
故答案为:D。
增加的表面积÷4=圆柱的底面积,圆柱的底面积×高=圆柱的体积,计算时注意单位的变化。
19.B
20.A
解:7个数字有4个偶数,3个奇数,大于3的数有3个,小于3的数有3个,
下面几种情况中发生的可能性最大的是球上的数是偶数。
故答案为:A。
可能性的大小与它在总数中所占数量的多少有关,在总数中占的数量多,摸到的可能性就大,占的数量小,摸到的可能性就小,占的数量相等,摸到的可能性也相等。
21.D
解:圆锥的底面直径是4米,底面半径是2米,
圆锥的体积:3.14×2×2×3÷3=12.56(立方米)
长方体的体积:4×4×2=32(立方米)
石顶屋的体积:12.56+32=44.56(立方米)
故答案为:D。
圆锥的体积=π×底面半径的平方×高÷3,长方体的体积=长×宽×高,圆锥的体积+长方体的体积=这个石顶屋的体积。
22.B
解:10:30-7:00=3.5小时
60×3.5=210(千米)
210÷100=2.1(厘米)
目的地应该是乙城。
故答案为:B。
行驶的速度×行驶的时间=行驶的路程,行驶的路程÷1厘米代表的长度=图上的长度,据此解答。
23.B
解:=300。7
故答案为:B
先求出杯子的容积:=h==300。牛奶的容积÷杯子的容积=至少需要的杯子数目。
24.A
25.B
解:2×2=4,2×3=6,4+6=10。
故答案为:B
烙2张饼按照正常方法烙,共需要2×2=4(分钟);剩下3张可以这样煎:第一次:放①的正面和②的正面,第二次:放①的反面和③的正面,第三次:放②的反面和③的反面,共用2×3=6(分钟);全部时间:4+6=10(分钟)。
26.D
解:小球的体积:
π×(18÷2)2×(10-8)
=π×81×2
=162π(立方厘米);
小正方体的体积:
π×(12÷2)2×26-π×(18÷2)2×8-162π
=π×36×26-π×81×8-162π
=936π-648π-162π
=126π(立方厘米);
(162π):(126π)=9:7。
故答案为:D。
放入小球后水面增高了,用减法求出增高了几厘米,因为增高的水的体积就是小球的体积,可根据圆柱的体积=πr2h,代入数据计算求出小球的体积;再根据第一个圆柱中原来有的高度是8厘米,及圆柱体的体积=πr2h,代入数据计算求出水的体积;因为两个容器的水的体积相同,再根据第二个圆柱的水的高度,求出总体积,再减去水的体积与小球的体积,即可求出小长方体的体积;最后根据比的意义,用小球的体积比小长方体的体积,然后化简比。
27.B
解:(2.33+2.10+2.82+2.23+2.18+2.82+2.25)÷7
=16.73÷7
=2.39(米)。
故答案为:B。
合适的数是这组数据的平均数,因为平均数能代表一组数据的总体水平。
28.D
29.C
30.C
解:A项:出勤人数+缺勤人数=全班人数,不成比例关系;
B项:总价÷数量=单价(一定), 单价一定,数量和总价成正比例关系;
C项:每天运的吨数×需要的天数=运送货物的总质量(一定),运送一批货物,每天运的吨数和需要的天数成反比例;
D项:圆的周长÷2÷半径=π(一定),圆的周长和半径成正比例。
故答案为:C。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
31.C
32.C
解:A项:三角形按角分为:直角三角形、钝角三角形、锐角三角形,原题干说法正确;
B项:正方形是特殊的长方形,长方形是特殊的平行四边形,原题干说法正确;
C项:垂直是相交的一种,原题干说法错误;
D项:正方体是特殊的长方体,还有圆柱、圆锥都是立体图形,原题干说法正确。
故答案为:C。
正方形是特殊的长方形,正方体是特殊的长方体,垂直是相交的一种情况。
33.B
解:A项:甲平均成绩低于28m;
B项:乙平均成绩大约28m;
C项:丙平均成绩高于28m;
D项:丁平均成绩低于28m。
故答案为:B。
平均数表示一组数据的整体水平,只有乙的成绩一次等于28米,一次成绩低于28米,剩余一次成绩高于28米,则平均成绩大约28米。
34.C
35.B
36.C
解:A、长方体是柱体,可以利用公式求体积;
B、是柱体,可以利用公式求体积;
C、是柱体,但不能用底面积×高计算体积;
D、长方体是柱体,可以利用公式求体积。
故答案为:C。
本题考查柱体的体积的公式,解题的关键是了解柱体的体积通项公式的运用条件。
37.B
38.D
39.B
40.C
41.B
42.A
解:60%÷15=0.04(平方厘米)
(1-60%)÷0.04
=0.4÷0.04
=10(厘米)。
故答案为:A。
把瓶子的容积看作单位"1",把瓶子的容积看作是水的体积和空气的体积之和,因为水的体积占瓶子容积的60%,则空气的体积占瓶子容积的(1-60%),假设瓶子底面积为 S ,瓶子倒放后水面距离瓶底的高度为 h 。则根据题意可得:15S=60%,Sh =40%,据此即可求出h。
43.A
解:在这个变化过程中,平行四边形的面积÷高=底(一定),平行四边形的面积和高成正比例。
故答案为:A。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
44.D
解:A项:15×10=150(平方厘米),原题干说法错误;
B项:(15+10+5)×4
=30×4
=120(厘米),原题干说法错误;
C项:15×10+(15×5+10×5)×2
=150+125×2
=150+250
=400(平方厘米),原题干说法错误;
D项:15×10×5
=150×5
=750(立方厘米),原题干说法正确。
故答案为:D。
A项:纸盒的底面积=长×宽;
B项:纸盒的棱长和=(长+宽+高)×4;
C项:纸盒的表面积=长×宽+(长×高+宽×高)×2;
D项:纸盒的体积=长×宽×高。
45.A
解:A项:去掉的体积是圆锥体积的2倍,原题干说法正确;
B项:π×(6÷2)2=9π,原题干说法错误;
C项:去掉的体积是圆柱体积的2倍,原题干说法错误;
D项:圆锥和圆柱体积的比是1:3,原题干说法错误。
故答案为:A。
圆锥的底面积=π×半径2,等底等高的圆柱的体积是圆锥体积的3倍,据此判断。
46.C
解:A项:运行的时间÷运行的周数=空间站绕地球运行一周的时间(一定),成正比例关系;
B项:冲厕水的总吨数÷年数=每年提供的冲厕水的吨数(一定),成正比例关系;
C项:书的单价 ×数量=小明带的钱数(一定),成反比例关系;
D项:单价=总价÷数量(一定),成正比例关系。
故答案为:C。
判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
47.D
解:A项:1.2×0.08=12×8×(0.1×0.01) ,原题干计算错误;
B项:120÷80=12÷8÷10 ,原题干计算错误;
C项:1.2×20=1.2×2×10 ,原题干计算错误;
D项:×=(3×6)×(×),原题干计算正确。
故答案为:D。
A项:1.2是一位小数,0.08是两位小数,所以1.2×0.08=12×8×(0.1×0.01) ;
B项:80=8×10,则120÷80=12÷8÷10 ;
C项:20=2×10,所以1.2×20=1.2×2×10 ;
D项:计算×时,可以先把各自计数单位的个数相乘,然后再乘它们分数单位的积。
48.C
解:A项:25%÷125%=20%,原题干说法正确;
B项:26÷12=2(人)······2(人)
2+1=3(人),原题干说法正确;
C项:y= x,则=4(一定),x和y成正比例,原题干说法错误;
D项:x+2y+1=6
3(x+2y+1)=6×3
3x +6 y +3=18,原题干说法正确。
故答案为:C。
A项:把女生人数看作单位“1”,男生人数是1+25%=125%,女生比男生少的分率=25%÷男生人数;
B项:抽屉原理,至少在同一抽屉里相同物体的个数=物体总个数÷抽屉的个数+1;
C项:判断两个相关联的量成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例;
D项:等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
49.D
50.C
51.D
52.A
53.D
(1)摆成正方形用的石头数÷4=一边用的石头数,一边用的石头数-1=一边的间隔数,一边的间隔数×1个间隔的长度=正方形的边长,正方形的边长×4=正方形的周长;
(2)计算小明家到湘湖的路程:根据题目,小明一家以40千米/小时的平均速度行驶了36分钟到达景区。首先,需要将36分钟转换为小时,然后,根据路程 = 速度 × 时间,计算路程;
(3)计算正方形圈的面积:已知正方形的周长是200厘米,因为正方形有四条边且每条边长相等,所以每条边长是50厘米,根据正方形的面积是边长的平方求出面积;
(4)分析圆柱形水桶的高与圆锥形漏斗高的关系:小明用圆锥形漏斗装满沙子,正好倒了两次把圆柱形水桶装满。这意味着圆柱形水桶的体积是圆锥形漏斗体积的两倍。由于圆柱形水桶和圆锥形漏斗的底面积一样大,所以我们可以根据圆柱与圆锥的体积公式来分析他们的高度关系;
(5)根据题意可知,起始点在坐标轴上部分,水满后一段时间内水位不变,水位下降后,水位比刚开始低,据此判断。
49.解:40÷4=10(颗)
10-1=9(个)
5×9=45(厘米)
45×4=180(厘米);
故答案为:D。
50.解:(小时),
(千米);
故答案为:C。
51.解:(厘米),
(平方厘米);
故答案为:D。
52.解:圆柱的体积为,圆锥的体积为,
由于 正好倒了两次把圆柱形水桶装满,
则,
简化后得到,
即圆柱形水桶的高是圆锥形漏斗高的;
故答案为:A。
53.解:由于小明盛了大半桶水,则起始点在坐标轴上部分,
把许多小石头放入桶里,溢出了一部分水,则水满后一段时间内水位不变,
把洗干净的小石头捞出,水位开始下降,
由于溢出了一部分水,则水位比刚开始低,
综上,D符合条件;
故答案为:D。
54.B
解:两面涂色的个数:12×(3-2)
=12×1
=12(个)
故答案为:B。
用n表示大正方体每条棱上小正方体的块数,三面涂色的小正方体的块数=8(顶点的个数);两面涂色的小正方体的块数=12×(n-2);一面涂色的小正方体的块数=6×(n-2)2;没有涂色的小正方体的块数=(n-2)3。
同课章节目录
