2024-2025学年苏教版六年级数学下册期末真题汇编专练02-填空题2(含答案+解析)
文档属性
| 名称 | 2024-2025学年苏教版六年级数学下册期末真题汇编专练02-填空题2(含答案+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 237.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-26 16:51:15 | ||
图片预览



文档简介
2024-2025学年苏教版六年级数学下册期末真题汇编
专练02-填空题2
一、填空题
1.(2024六下·肇庆期末)2023年5月10日21时22分,搭载天舟六号货运飞船的长征七号遥七运载火箭发射成功。火箭喷射时的温度最高可达到零上3000摄氏度,记作 摄氏度;而在火箭舱体中,则是零下183摄氏度,记作 摄氏度。
2.(2024六下·灵川期末)在比例尺是1∶2000的图上,量得学校操场长6厘米,宽3厘米。学校操场的实际面积是 平方米。
3.(2024六下·奉化期末)( )∶30=0.8==( )%=( )折。
4.(2024六下·双流期末)在比例尺为1∶5000000的地图上量得一条大河的长度为3厘米,则这条大河的实际长度是 千米。
5.(2024六下·黔西南期末)将一块棱长为6cm的正方体铁块放入一个底面直径8cm、高10cm、水深7cm的圆柱形容器中,水溢出 cm3。
6.(2024六下·黔西南期末)田里有一个麦堆,其形状近似于直径2m,高1.5m的圆锥。麦堆的体积大约是 m3。如果每立方米麦子大约重0.8t,这堆麦子大约重 t。
7.(2024六下·黔西南期末)如果月收入在5000~8000元范围内,那么超过5000元的部分应按3%缴纳个人所得税。李阿姨的月工资是6800元,她每月应缴纳个人所得税 元。
8.(2024六下·黔西南期末)如表中m和n是两个相关联的量。
(1)当时,m与n成 比例关系。
m 6 x
n 3
(2)当x= 时,m与n成反比例关系。
9.(2024六下·黔西南期末)一个半径3cm,高10cm圆柱的展开图如图所示,这个圆柱的侧面展开图的长是 cm,宽是 cm,这个圆柱的侧面积是 cm2,表面积是 cm2,体积是 cm3。
10.(2024六下·黔西南期末)万峰湖地处黔西南布依族苗族自治州首府——兴义市的东南部,坐落于马岭河下游,享有“万峰之湖,西南之最,南国风光,山水画卷”之美誉。如果万峰湖湖水的警戒水位记为0m,正数表示水面高于警戒水位,那么汛期水位高于警戒水位1.3m,记为 m,读作 米;旱季水位低于警戒水位2m,记为 m,读作 米。
11.(2024六下·东莞期末)在一个比例中,两个内项互为倒数。已知一个内项是,那么另一个内项是 。
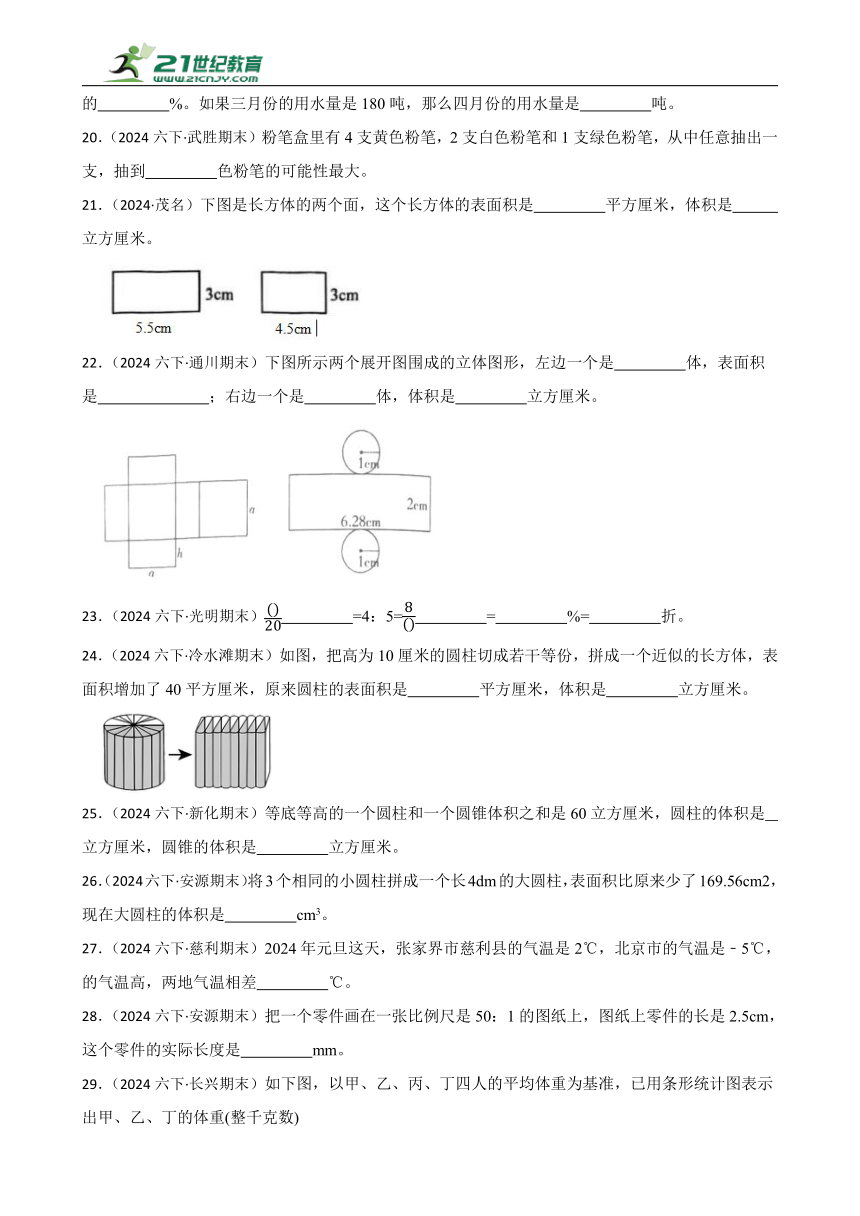
12.(2024六下·东莞期末) = :40=0.3= %= (填成数)。
13.(2024六下·凉山期末) 一个长方体的棱长总和是48厘米,长、宽、高的比是3:2:1,这个长方体的表面积是 平方厘米,体积是 立方厘米。
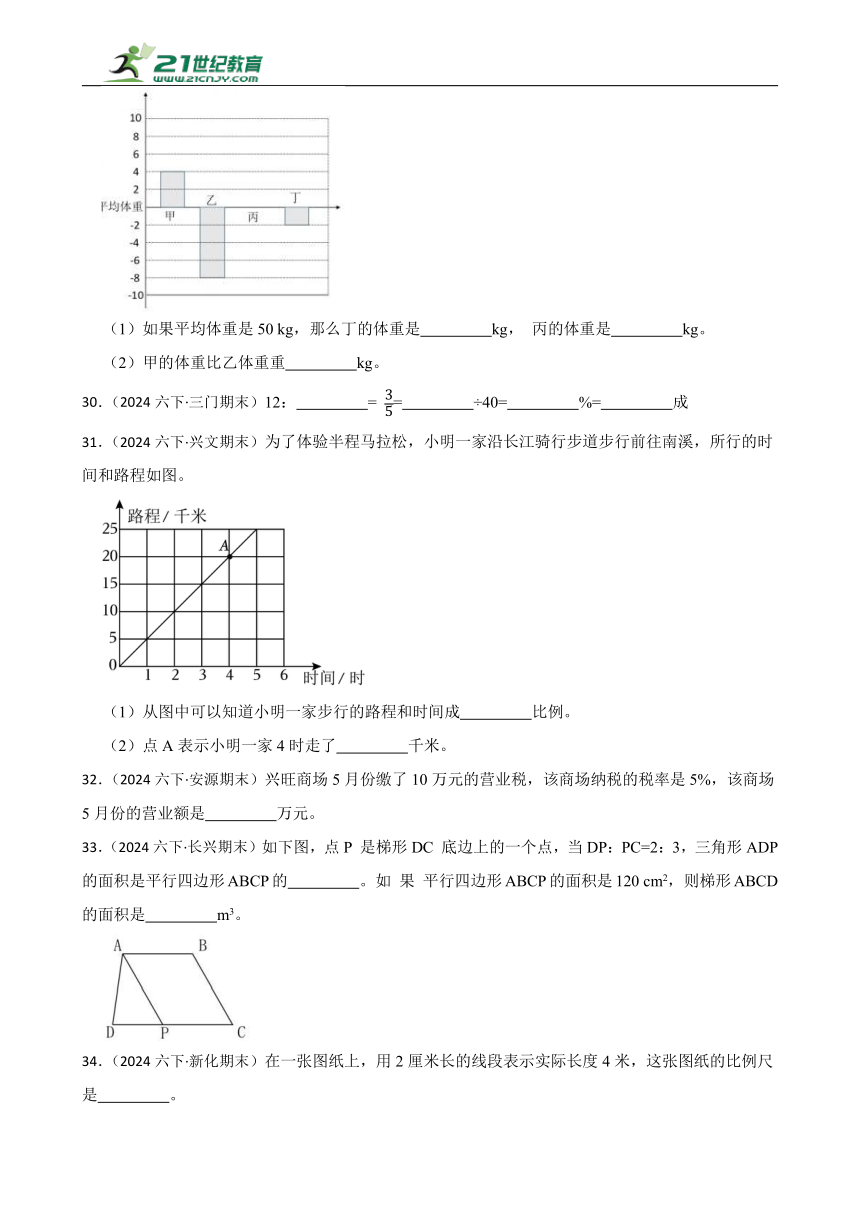
14.(2024六下·武胜期末)甲、乙、丙三个商店同时销售一种原价为每袋6元的洗衣粉。甲商店打八五折;乙商店满100元打七五折:丙商店买4送1。王阿姨要买10袋这种洗衣粉,想花钱最少,应该到 商店去买。
15.(2024六下·武胜期末)某班有48人,某次数学测试的优秀率是25%,获得优秀的有 人,如果将这次数学测试成绩制成扇形统计图,表示优秀的扇形的圆心角度数是 。
16.(2024六下·武胜期末)如下图,圆柱形容器是空的,长方体容器中水深6.28cm,要将长方体容器中的水全部倒入圆柱形容器,这时水深 cm;如果倒入与这个圆柱形的底面积之比是5:1的圆锥形容器中,水面高 cm。
17.(2024六下·武胜期末)在比例8:32=4:16中,如果把内项32减少8,要使比例成立,那么外项8应减少
18.(2024六下·武胜期末)把一个圆柱削成一个最大的圆锥,削去部分的体积与圆锥的体积比是 : 。
19.(2024六下·安源期末)阳光小学四月份的用水量比三月份增加二成,四月份的用水量是三月份的 %。如果三月份的用水量是180吨,那么四月份的用水量是 吨。
20.(2024六下·武胜期末)粉笔盒里有4支黄色粉笔,2支白色粉笔和1支绿色粉笔,从中任意抽出一支,抽到 色粉笔的可能性最大。
21.(2024·茂名)下图是长方体的两个面,这个长方体的表面积是 平方厘米,体积是 立方厘米。
22.(2024六下·通川期末)下图所示两个展开图围成的立体图形,左边一个是 体,表面积是 ;右边一个是 体,体积是 立方厘米。
23.(2024六下·光明期末) =4:5= = %= 折。
24.(2024六下·冷水滩期末)如图,把高为10厘米的圆柱切成若干等份,拼成一个近似的长方体,表面积增加了40平方厘米,原来圆柱的表面积是 平方厘米,体积是 立方厘米。
25.(2024六下·新化期末)等底等高的一个圆柱和一个圆锥体积之和是60立方厘米,圆柱的体积是 立方厘米,圆锥的体积是 立方厘米。
26.(2024六下·安源期末)将3个相同的小圆柱拼成一个长4dm的大圆柱,表面积比原来少了169.56cm2,现在大圆柱的体积是 cm3。
27.(2024六下·慈利期末)2024年元旦这天,张家界市慈利县的气温是2℃,北京市的气温是﹣5℃, 的气温高,两地气温相差 ℃。
28.(2024六下·安源期末)把一个零件画在一张比例尺是50:1的图纸上,图纸上零件的长是2.5cm,这个零件的实际长度是 mm。
29.(2024六下·长兴期末)如下图,以甲、乙、丙、丁四人的平均体重为基准,已用条形统计图表示出甲、乙、丁的体重(整千克数)
(1)如果平均体重是50 kg,那么丁的体重是 kg, 丙的体重是 kg。
(2)甲的体重比乙体重重 kg。
30.(2024六下·三门期末)12: = = ÷40= %= 成
31.(2024六下·兴文期末)为了体验半程马拉松,小明一家沿长江骑行步道步行前往南溪,所行的时间和路程如图。
(1)从图中可以知道小明一家步行的路程和时间成 比例。
(2)点A表示小明一家4时走了 千米。
32.(2024六下·安源期末)兴旺商场5月份缴了10万元的营业税,该商场纳税的税率是5%,该商场5月份的营业额是 万元。
33.(2024六下·长兴期末)如下图,点P 是梯形DC 底边上的一个点,当DP:PC=2:3,三角形ADP的面积是平行四边形ABCP的 。 如 果 平行四边形ABCP的面积是120 cm2, 则梯形ABCD的面积是 m3。
34.(2024六下·新化期末)在一张图纸上,用2厘米长的线段表示实际长度4米,这张图纸的比例尺是 。
35.(2024六下·冷水滩期末)等底等高的圆柱和圆锥,它们的体积相差32立方厘米,这个圆锥的体积是 立方厘米,圆柱的体积是 立方厘米。
36.(2024六下·萧山期末)两个正方体的体积比是64:27,那么小正方体的棱长是大正方体棱长的 。
37.(2024六下·安源期末)如图是圆柱的表面展开图,则圆柱的高是 cm,侧面积是 cm2,体积是 cm3.
38.(2024六下·冷水滩期末)2023年12月26日,永州湘江东路正式通车,全长14.3km,把它画在比例尺为的图纸上,应画 cm。
39.(2024六下·安源期末) :20= = %=4÷ = 折=二成五。
40.(2024六下·冷水滩期末)某班一次数学测验的平均成绩是88分,老师把90分记作“﹢2分”,那么“﹣2分”表示实际得分 分,82.5分记作 分。
41.(2024六下·三门期末)如下图, 把一个底面直径是 6 厘米, 高10厘米的圆桂, 切成16等份后拼成一个近似的长方体。拼成的长方体的体积是 立方厘米,拼成的长方体表面积比圆柱表面积多了 平方厘米。
42.(2024六下·三门期末)在比例尺为 的浙江地图上, 量得台州到杭州的图上距密是6厘米, 则两地的实际距离是 千米; 如果在另一幅地图上是得两地的图上距齐是3厘米, 那么这幅地图的比例尺是 。
43.(2024六下·奉化期末)宁波至象山的城际铁路全长约60千米,总投资约25190000000元,设计时速为160千米/时,2027年正式通车后,将大大缩短宁波到象山的时间。
(1)横线上的数读作 ,省略亿位后面的尾数,约是 亿元。
(2)把城际铁路全长画在一张比例尺为1∶500000的地图上,图上距离是 厘米。
44.(2024六下·慈利期末)一个圆柱的底面半径是3分米,侧面展开后正好是一个正方形,圆柱的高是 分米,底面积是 。
45.(2024六下·兴文期末)一个圆锥,底面周长扩大到原来的3倍,高不变,体积扩大到原来的 倍。
46.(2024六下·兴文期末)一个零件的长度是4mm,画在图纸上的长是8cm,这幅图的比例尺是 。
47.(2024六下·冷水滩期末)有25个零件,其中有一个轻一点,用天平称,至少称 次,就能找到这个轻一点的零件。
48.(2024六下·兴文期末)把桌面上水平放置的一个半径为5cm的圆形纸片,垂直向上平移6cm,所形成立体图形的体积是 cm3。
49.(2024六下·湛江期末)将棱长为3厘米的小正方体按如图方式摆放在地上,露在外面的面积是 cm2,这个图的体积是 cm3。
50.(2024六下·湛江期末)一个圆柱和一个圆锥等底等高,它们的体积之和是48立方分米,那么圆柱的体积是 立方分米,圆锥的体积是 立方分米。
答案解析部分
1.﹢3000;﹣183
2.7200
3.24;4;80;八
解:0.8==
=4÷5=4×6÷5×6=24÷30=24:30
0.8=80%=八折
故答案为:24;4;80;八。
首先将小数化成分母为10的分数,再化简成最简分数;将分数转化为整数相除,被除数和除数同时乘以6,在商不变的前提下将除数变为30;再将整数除法转化为比,被除数相当于比的前项,除数相当于比的后项,除号相当于比号;小数化成百分数,小数点向右移动两位,同时在数的后面添上百分号;根据折扣的意义,百分之几十就是几折。
4.150
5.65.28
6.1.57;1.256
7.54
8.(1)正
(2)72
9.18.84;10;188.4;244.92;282.6
10.+1.3;正一点三;﹣2;负二
11.
解:两个内项互为倒数,两个内项的积是1,
1÷=,另一个内项是。
故答案为:。
比例的两个外项之积÷其中一个内项=另一个内项。
12.50;12;30;三成
解:0.3====12:40;
0.3=30%=三成。
故答案为:50;12;30;三成。
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变;
小数化百分数:把小数点向右移动两位,同时在后面添上百分号;几成表示百分之几十;
分数可以写成比的形式,分子是比的前项,分母是比的后项。
13.88;48
解:3+2+1=6,
长:48÷4×
=12×
=6(厘米),
宽:48÷4×
=12×
=4(厘米),
高:48÷4×
=12×
=2(厘米),
表面积:(6×4+6×2+4×2)×2
=(24+12+8)×2
=44×2
=88(平方厘米),
体积:6×4×2
=24×2
=48(立方厘米)。
故答案为:88;48。
长方体的棱长总和=(长+宽+高)×4,已知长方体的棱长总和是48厘米,长、宽、高的比是3:2:1,据此可以求出长宽、高,再根据长方体的表面积公式:S=(ab+ah+bh)×2,体积公式:V=abh,把数据代入公式解答。
14.丙
解:甲商店:85%×6×10=51(元);
乙商店:6×10=60(元);
丙商店:6×[10÷(4+1)×4]=6×8=48(元)
51>60>48,应该到丙商店去买。
故答案为:丙。
甲商店:用每袋的钱数乘袋数求出总价,再乘85%即可求出售价;
乙商店:用每袋的钱数乘袋数求出总价,总价低于100元就不打折;
丙商店:每(4+1)袋中有1袋是送的,4袋是付款的,因此用10除以(4+1)再乘4就是需要付钱的袋数,再乘每袋的钱数即可求出总价;比较后判断去哪个商店买即可。
15.12;90°
解:获得优秀的:48×25%=12(人);
圆心角度数:360°×25%=90°。
故答案为:12;90°。
用总人数乘优秀率即可求出获得优秀的人数。优秀率是25%,那么用扇形统计图表示优秀人数时扇形的圆心角就是360°的25%,由此求出圆心角的度数即可。
16.8;4.8
解:第一问:
10×10×6.28÷[3.14×(10÷2)2]
=628÷3.14÷25
=8(cm)
第二问:1×8÷5÷=4.8(cm)
故答案为:8;4.8。
首先根据长方体的体积公式:V=abh,求出乙长方体容器中水的体积,然后用水的体积除以圆柱形容器的底面积即可求出水深;求如果倒入与这个圆柱底面积之比是5:1的圆锥形容器中水面高,把这个圆柱底面积看作1,则圆锥形容器的底面积看作5,根据圆柱体积公式,用底面积乘高再除以圆锥形容器的底面积再除以即可。
17.2
解:8÷32=,8×=2,所以外项8应减少2。
故答案为:2。
表示两个比相等的式子叫做比例。8:32中,32减少8,也就是减少了32的,所以要把8也少即可。
18.2;1
解:把一个圆柱削成一个最大的圆锥,削去部分的体积与圆锥的体积比是2:1。
故答案为:2;1。
把圆柱削成最大的圆锥,这个圆锥与圆柱等底等高,等底等高的圆柱体积是圆锥体积的3倍,圆锥的体积是1份,削去部分就是2份,所以削去部分的体积与圆锥的体积比是2:1。
19.120;216
解:四月份的用水量是三月份的1+20%=120%;
四月份的用水量:180×120%=216(吨)。
故答案为:120;216。
二成就是20%,以三月份的用水量为单位“1”,用1加上20%即可求出四月份的用水量是三月份的百分之几。用三月份的用水量乘四月份占三月份的百分率即可求出四月份的用水量。
20.黄
解:粉笔盒里有4支黄色粉笔,2支白色粉笔和1支绿色粉笔,从中任意抽出一支,抽到黄色粉笔的可能性最大。
故答案为:黄。共三种颜色的粉笔,抽到哪种颜色的粉笔都有可能,哪种颜色的粉笔最多,抽到这种颜色的康乃馨就最大。
21.109.5;74.25
解:(5.5×4.5+3×4.5 +5.5×3) ×2(24.75+13.5 +16.5)×2= 54.75×2= 109.5(平方厘米)
5.5×4.5×3=24×3= 74.25(立方厘米)
故答案为:109.5;74.25
长方体的表面积=(长×宽+长×高+宽×高)×2 。长方体的体积=长×宽×高
22.长方;2+4ah;圆柱;6.28
解:(a×a+a×h+a×h)×2=(+2ah)×2=2+4ah
左边一个是长方体,表面积是2+4ah;
3.14×1×1×2=6.28(立方厘米)
右边一个是圆柱体,体积是6.28立方厘米。
故答案为:长方;2+4ah;圆柱;6.28。
(长×宽+长×高+宽×高)×2=长方体的表面积;π×底面半径的平方×高=圆柱的体积。
23.16;10;80;八
解:4:5===;;4:5=0.8=80%=八折。
故答案为:16;10;80;八。
比的前项相当于分数的分子,后项相当于分母。根据分数与比的关系结合分数的基本性质确定分子或分母。用前项除以后项求出比值,再化成百分数;根据百分数确定折扣即可。
24.150.72;125.6
25.45;15
26.1695.6
解:169.56÷4=42.39(cm2),4dm=40cm,体积:42.39×40=1695.6(cm3)。
故答案为:1695.6。
把3个相同的圆柱拼成一个大圆柱,表面积会比原来3个小圆柱的表面积之和减少了4个底面的面积,因此用表面积减少的部分除以4求出底面积,再用底面积乘大圆柱的高即可求出大圆柱的体积。注意统一单位。
27.慈利县;7
28.0.5
解:2.5cm=25mm,25÷50=0.5(mm)。
故答案为:0.5。
50:1的意思就是图上距离是实际距离的50倍,所以用图上距离除以50即可求出实际距离。注意换算单位。
29.(1)48;56
(2)12
解:(1)甲的体重为50+4=54(kg),乙的体重为50-8=42(kg),丁的体重为50-2=48(kg)
甲、乙、丙、丁四人的体重和=50×4=200(kg),甲、乙、丁三人的体重和为54+42+48=144(kg),所以丙的体重为200-144=56(kg);
(2)已知甲的体重为54kg,乙的体重为42kg,所以甲的体重比乙体重重54-42=12(kg)。
故答案为:(1)48;56(2)12。
(1)观察条形图得出甲、乙、丁三人的体重,进而根据平均体重=,得出丙的体重;
(2)用甲的体重减去乙的体重即为甲的体重比乙体重重的千克数。
30.20;24;60;六
解:=(3×4):(5×4)=12:20;
=(3×8)÷(5×8)=24÷40;
=3÷5=0.6=60%=六成;
所以12:20==24÷40=60%=六成。
故答案为:20;24;60;六。
比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变;分数化成百分数,用分数的分子除以分母化成小数,然后把小数的小数点向右移动两位,再加上百分号;百分之几十就等于几成。
31.(1)正
(2)20
32.200
解:10÷5%=200(万元)
故答案为:200。
税率是缴纳的税额与营业额的比率,用缴纳的营业税除以税率即可求出该月的营业额。
33.;0.016
解:三角形ADP的面积=×DP×高,平行四边形ABCP的面积=PC×高,三角形ADP的高与平行四边形ABCP的高相等;
又因为DP:PC=2:3,根据比例的基本性质,得到2PC=3DP,故PC=DP,平行四边形ABCP的面积=DP×高;
==×=,故三角形ADP的面积是平行四边形ABCP的;
已知平行四边形ABCP的面积是120 cm2,所以三角形ADP的面积=平行四边形ABCP的面积=×120=40(cm2);
梯形面积=120+40=160(cm2)=0.016(cm2)。
故答案为:;0.016。
根据面积公式:三角形面积=×底×高,平行四边形面积=底×高,以及比例的基本性质:外项积等于内项积,列出关于三角形和平行四边形面积的式子,两个式子作比即可求出三角形ADP的面积是平行四边形ABCP的多少;
梯形面积=三角形面积=平行四边形面积,根据第一空所得的三角形ADP的面积是平行四边形ABCP的面积的关系,以及题干中告诉的平行四边形的面积求出三角形的面积,进而求出梯形ABCD的面积,并将所求面积单位平方厘米换算成题干中的平方米。
34.1∶200
35.16;48
36.
解:64:27=:,
两个正方体的体积比是64:27,两个正方体的棱长比是4:3,
3÷4=,小正方体的棱长是大正方体棱长的。
故答案为:。
正方体的体积=棱长×棱长×棱长,小正方体的棱长÷大正方体的棱长=小正方体的棱长是大正方体棱长的几分之几。
37.3;18.84;9.42
解:圆柱的高是3cm;侧面积:6.28×3=18.84(cm2);底面半径:6.28÷3.14÷2=1(cm),体积:3.14×12×3=9.42(cm3)。
故答案为:3;18.84;9.42。
根据图形可知,6.28cm是底面周长,高是3cm。用底面周长乘高求出侧面积。用底面周长除以3.14再除以2求出底面半径,然后用底面积乘高求出体积即可。
38.2.86
39.5;4;25;16;二五
解:二成五=25%;20×25%=5;4÷25%=16;所以5:20==25%=4÷16=二五折=二成五。
故答案为:5;4;25;16;二五。
二成五就是25%。用后项乘25%求出前项;用被除数除以25%求出除数;把25%写成分母是100的分数并化成最简分数;根据百分数确定折扣即可。
40.86;-5.5
41.282.6;60
解:3.14 × (6 ÷2)2×10=3.14×9×10=28.26×10= 282.6(立方厘米)
底面半径:6÷2=3(厘米)10×3 ×2=30×2=60(平方厘米)
故答案为:282.6;60
根据圆柱体积公式的推导过程可知:把圆柱切拼成一个近似长方体后体积不变。拼成的长方体的表面积把圆柱的表面积增加了两个切面的面积,根据圆柱的体积公式:V= πr2h,长方形的面积公式:S =ab,把数据代入公式解答。
42.300;
解:实际距离==厘米=千米。实际距离,即,简化比例尺为。
故答案为:300;
图上距离:实际距离=比例尺,据此回答即可。
43.(1)二百五十一亿九千万;252
(2)12
解:(1)横线上的数25190000000读作二百五十一亿九千万,省略亿位后面的尾数,约是252亿元。
(2)60千米=6000000厘米
6000000×=12(厘米)
把城际铁路全长画在一张比例尺为1∶500000的地图上,图上距离是12厘米。
故答案为:二百五十一亿九千万;252;12。
(1)要读亿以上数, 亿以上的数的读法:先分级,再从高位读起,读完亿级或万级的数,要加上”亿“字或”万“字,每级末尾不管有几个0都不读,其他数位有一个0或连续几个0,都只读一个0。
改写成用“亿”作单位的数,小数点向左移动8位,再在后面加上一个“亿”字,注意要用四舍五入舍去亿后面的数字。
(2)先把60千米化为6000000厘米,再根据图上距离=实际距离×比例尺,求出60千米的图上距离。
(1)25190000000读作二百五十一亿九千万,省略亿位后面的尾数,约是252亿元。
(2)60千米=6000000厘米
6000000×=12(厘米)
把城际铁路全长画在一张比例尺为1∶500000的地图上,图上距离是12厘米。
44.18.84;28.26平方分米
45.9
46.20∶1
47.3
48.471
49.216;243
50.36;12
专练02-填空题2
一、填空题
1.(2024六下·肇庆期末)2023年5月10日21时22分,搭载天舟六号货运飞船的长征七号遥七运载火箭发射成功。火箭喷射时的温度最高可达到零上3000摄氏度,记作 摄氏度;而在火箭舱体中,则是零下183摄氏度,记作 摄氏度。
2.(2024六下·灵川期末)在比例尺是1∶2000的图上,量得学校操场长6厘米,宽3厘米。学校操场的实际面积是 平方米。
3.(2024六下·奉化期末)( )∶30=0.8==( )%=( )折。
4.(2024六下·双流期末)在比例尺为1∶5000000的地图上量得一条大河的长度为3厘米,则这条大河的实际长度是 千米。
5.(2024六下·黔西南期末)将一块棱长为6cm的正方体铁块放入一个底面直径8cm、高10cm、水深7cm的圆柱形容器中,水溢出 cm3。
6.(2024六下·黔西南期末)田里有一个麦堆,其形状近似于直径2m,高1.5m的圆锥。麦堆的体积大约是 m3。如果每立方米麦子大约重0.8t,这堆麦子大约重 t。
7.(2024六下·黔西南期末)如果月收入在5000~8000元范围内,那么超过5000元的部分应按3%缴纳个人所得税。李阿姨的月工资是6800元,她每月应缴纳个人所得税 元。
8.(2024六下·黔西南期末)如表中m和n是两个相关联的量。
(1)当时,m与n成 比例关系。
m 6 x
n 3
(2)当x= 时,m与n成反比例关系。
9.(2024六下·黔西南期末)一个半径3cm,高10cm圆柱的展开图如图所示,这个圆柱的侧面展开图的长是 cm,宽是 cm,这个圆柱的侧面积是 cm2,表面积是 cm2,体积是 cm3。
10.(2024六下·黔西南期末)万峰湖地处黔西南布依族苗族自治州首府——兴义市的东南部,坐落于马岭河下游,享有“万峰之湖,西南之最,南国风光,山水画卷”之美誉。如果万峰湖湖水的警戒水位记为0m,正数表示水面高于警戒水位,那么汛期水位高于警戒水位1.3m,记为 m,读作 米;旱季水位低于警戒水位2m,记为 m,读作 米。
11.(2024六下·东莞期末)在一个比例中,两个内项互为倒数。已知一个内项是,那么另一个内项是 。
12.(2024六下·东莞期末) = :40=0.3= %= (填成数)。
13.(2024六下·凉山期末) 一个长方体的棱长总和是48厘米,长、宽、高的比是3:2:1,这个长方体的表面积是 平方厘米,体积是 立方厘米。
14.(2024六下·武胜期末)甲、乙、丙三个商店同时销售一种原价为每袋6元的洗衣粉。甲商店打八五折;乙商店满100元打七五折:丙商店买4送1。王阿姨要买10袋这种洗衣粉,想花钱最少,应该到 商店去买。
15.(2024六下·武胜期末)某班有48人,某次数学测试的优秀率是25%,获得优秀的有 人,如果将这次数学测试成绩制成扇形统计图,表示优秀的扇形的圆心角度数是 。
16.(2024六下·武胜期末)如下图,圆柱形容器是空的,长方体容器中水深6.28cm,要将长方体容器中的水全部倒入圆柱形容器,这时水深 cm;如果倒入与这个圆柱形的底面积之比是5:1的圆锥形容器中,水面高 cm。
17.(2024六下·武胜期末)在比例8:32=4:16中,如果把内项32减少8,要使比例成立,那么外项8应减少
18.(2024六下·武胜期末)把一个圆柱削成一个最大的圆锥,削去部分的体积与圆锥的体积比是 : 。
19.(2024六下·安源期末)阳光小学四月份的用水量比三月份增加二成,四月份的用水量是三月份的 %。如果三月份的用水量是180吨,那么四月份的用水量是 吨。
20.(2024六下·武胜期末)粉笔盒里有4支黄色粉笔,2支白色粉笔和1支绿色粉笔,从中任意抽出一支,抽到 色粉笔的可能性最大。
21.(2024·茂名)下图是长方体的两个面,这个长方体的表面积是 平方厘米,体积是 立方厘米。
22.(2024六下·通川期末)下图所示两个展开图围成的立体图形,左边一个是 体,表面积是 ;右边一个是 体,体积是 立方厘米。
23.(2024六下·光明期末) =4:5= = %= 折。
24.(2024六下·冷水滩期末)如图,把高为10厘米的圆柱切成若干等份,拼成一个近似的长方体,表面积增加了40平方厘米,原来圆柱的表面积是 平方厘米,体积是 立方厘米。
25.(2024六下·新化期末)等底等高的一个圆柱和一个圆锥体积之和是60立方厘米,圆柱的体积是 立方厘米,圆锥的体积是 立方厘米。
26.(2024六下·安源期末)将3个相同的小圆柱拼成一个长4dm的大圆柱,表面积比原来少了169.56cm2,现在大圆柱的体积是 cm3。
27.(2024六下·慈利期末)2024年元旦这天,张家界市慈利县的气温是2℃,北京市的气温是﹣5℃, 的气温高,两地气温相差 ℃。
28.(2024六下·安源期末)把一个零件画在一张比例尺是50:1的图纸上,图纸上零件的长是2.5cm,这个零件的实际长度是 mm。
29.(2024六下·长兴期末)如下图,以甲、乙、丙、丁四人的平均体重为基准,已用条形统计图表示出甲、乙、丁的体重(整千克数)
(1)如果平均体重是50 kg,那么丁的体重是 kg, 丙的体重是 kg。
(2)甲的体重比乙体重重 kg。
30.(2024六下·三门期末)12: = = ÷40= %= 成
31.(2024六下·兴文期末)为了体验半程马拉松,小明一家沿长江骑行步道步行前往南溪,所行的时间和路程如图。
(1)从图中可以知道小明一家步行的路程和时间成 比例。
(2)点A表示小明一家4时走了 千米。
32.(2024六下·安源期末)兴旺商场5月份缴了10万元的营业税,该商场纳税的税率是5%,该商场5月份的营业额是 万元。
33.(2024六下·长兴期末)如下图,点P 是梯形DC 底边上的一个点,当DP:PC=2:3,三角形ADP的面积是平行四边形ABCP的 。 如 果 平行四边形ABCP的面积是120 cm2, 则梯形ABCD的面积是 m3。
34.(2024六下·新化期末)在一张图纸上,用2厘米长的线段表示实际长度4米,这张图纸的比例尺是 。
35.(2024六下·冷水滩期末)等底等高的圆柱和圆锥,它们的体积相差32立方厘米,这个圆锥的体积是 立方厘米,圆柱的体积是 立方厘米。
36.(2024六下·萧山期末)两个正方体的体积比是64:27,那么小正方体的棱长是大正方体棱长的 。
37.(2024六下·安源期末)如图是圆柱的表面展开图,则圆柱的高是 cm,侧面积是 cm2,体积是 cm3.
38.(2024六下·冷水滩期末)2023年12月26日,永州湘江东路正式通车,全长14.3km,把它画在比例尺为的图纸上,应画 cm。
39.(2024六下·安源期末) :20= = %=4÷ = 折=二成五。
40.(2024六下·冷水滩期末)某班一次数学测验的平均成绩是88分,老师把90分记作“﹢2分”,那么“﹣2分”表示实际得分 分,82.5分记作 分。
41.(2024六下·三门期末)如下图, 把一个底面直径是 6 厘米, 高10厘米的圆桂, 切成16等份后拼成一个近似的长方体。拼成的长方体的体积是 立方厘米,拼成的长方体表面积比圆柱表面积多了 平方厘米。
42.(2024六下·三门期末)在比例尺为 的浙江地图上, 量得台州到杭州的图上距密是6厘米, 则两地的实际距离是 千米; 如果在另一幅地图上是得两地的图上距齐是3厘米, 那么这幅地图的比例尺是 。
43.(2024六下·奉化期末)宁波至象山的城际铁路全长约60千米,总投资约25190000000元,设计时速为160千米/时,2027年正式通车后,将大大缩短宁波到象山的时间。
(1)横线上的数读作 ,省略亿位后面的尾数,约是 亿元。
(2)把城际铁路全长画在一张比例尺为1∶500000的地图上,图上距离是 厘米。
44.(2024六下·慈利期末)一个圆柱的底面半径是3分米,侧面展开后正好是一个正方形,圆柱的高是 分米,底面积是 。
45.(2024六下·兴文期末)一个圆锥,底面周长扩大到原来的3倍,高不变,体积扩大到原来的 倍。
46.(2024六下·兴文期末)一个零件的长度是4mm,画在图纸上的长是8cm,这幅图的比例尺是 。
47.(2024六下·冷水滩期末)有25个零件,其中有一个轻一点,用天平称,至少称 次,就能找到这个轻一点的零件。
48.(2024六下·兴文期末)把桌面上水平放置的一个半径为5cm的圆形纸片,垂直向上平移6cm,所形成立体图形的体积是 cm3。
49.(2024六下·湛江期末)将棱长为3厘米的小正方体按如图方式摆放在地上,露在外面的面积是 cm2,这个图的体积是 cm3。
50.(2024六下·湛江期末)一个圆柱和一个圆锥等底等高,它们的体积之和是48立方分米,那么圆柱的体积是 立方分米,圆锥的体积是 立方分米。
答案解析部分
1.﹢3000;﹣183
2.7200
3.24;4;80;八
解:0.8==
=4÷5=4×6÷5×6=24÷30=24:30
0.8=80%=八折
故答案为:24;4;80;八。
首先将小数化成分母为10的分数,再化简成最简分数;将分数转化为整数相除,被除数和除数同时乘以6,在商不变的前提下将除数变为30;再将整数除法转化为比,被除数相当于比的前项,除数相当于比的后项,除号相当于比号;小数化成百分数,小数点向右移动两位,同时在数的后面添上百分号;根据折扣的意义,百分之几十就是几折。
4.150
5.65.28
6.1.57;1.256
7.54
8.(1)正
(2)72
9.18.84;10;188.4;244.92;282.6
10.+1.3;正一点三;﹣2;负二
11.
解:两个内项互为倒数,两个内项的积是1,
1÷=,另一个内项是。
故答案为:。
比例的两个外项之积÷其中一个内项=另一个内项。
12.50;12;30;三成
解:0.3====12:40;
0.3=30%=三成。
故答案为:50;12;30;三成。
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变;
小数化百分数:把小数点向右移动两位,同时在后面添上百分号;几成表示百分之几十;
分数可以写成比的形式,分子是比的前项,分母是比的后项。
13.88;48
解:3+2+1=6,
长:48÷4×
=12×
=6(厘米),
宽:48÷4×
=12×
=4(厘米),
高:48÷4×
=12×
=2(厘米),
表面积:(6×4+6×2+4×2)×2
=(24+12+8)×2
=44×2
=88(平方厘米),
体积:6×4×2
=24×2
=48(立方厘米)。
故答案为:88;48。
长方体的棱长总和=(长+宽+高)×4,已知长方体的棱长总和是48厘米,长、宽、高的比是3:2:1,据此可以求出长宽、高,再根据长方体的表面积公式:S=(ab+ah+bh)×2,体积公式:V=abh,把数据代入公式解答。
14.丙
解:甲商店:85%×6×10=51(元);
乙商店:6×10=60(元);
丙商店:6×[10÷(4+1)×4]=6×8=48(元)
51>60>48,应该到丙商店去买。
故答案为:丙。
甲商店:用每袋的钱数乘袋数求出总价,再乘85%即可求出售价;
乙商店:用每袋的钱数乘袋数求出总价,总价低于100元就不打折;
丙商店:每(4+1)袋中有1袋是送的,4袋是付款的,因此用10除以(4+1)再乘4就是需要付钱的袋数,再乘每袋的钱数即可求出总价;比较后判断去哪个商店买即可。
15.12;90°
解:获得优秀的:48×25%=12(人);
圆心角度数:360°×25%=90°。
故答案为:12;90°。
用总人数乘优秀率即可求出获得优秀的人数。优秀率是25%,那么用扇形统计图表示优秀人数时扇形的圆心角就是360°的25%,由此求出圆心角的度数即可。
16.8;4.8
解:第一问:
10×10×6.28÷[3.14×(10÷2)2]
=628÷3.14÷25
=8(cm)
第二问:1×8÷5÷=4.8(cm)
故答案为:8;4.8。
首先根据长方体的体积公式:V=abh,求出乙长方体容器中水的体积,然后用水的体积除以圆柱形容器的底面积即可求出水深;求如果倒入与这个圆柱底面积之比是5:1的圆锥形容器中水面高,把这个圆柱底面积看作1,则圆锥形容器的底面积看作5,根据圆柱体积公式,用底面积乘高再除以圆锥形容器的底面积再除以即可。
17.2
解:8÷32=,8×=2,所以外项8应减少2。
故答案为:2。
表示两个比相等的式子叫做比例。8:32中,32减少8,也就是减少了32的,所以要把8也少即可。
18.2;1
解:把一个圆柱削成一个最大的圆锥,削去部分的体积与圆锥的体积比是2:1。
故答案为:2;1。
把圆柱削成最大的圆锥,这个圆锥与圆柱等底等高,等底等高的圆柱体积是圆锥体积的3倍,圆锥的体积是1份,削去部分就是2份,所以削去部分的体积与圆锥的体积比是2:1。
19.120;216
解:四月份的用水量是三月份的1+20%=120%;
四月份的用水量:180×120%=216(吨)。
故答案为:120;216。
二成就是20%,以三月份的用水量为单位“1”,用1加上20%即可求出四月份的用水量是三月份的百分之几。用三月份的用水量乘四月份占三月份的百分率即可求出四月份的用水量。
20.黄
解:粉笔盒里有4支黄色粉笔,2支白色粉笔和1支绿色粉笔,从中任意抽出一支,抽到黄色粉笔的可能性最大。
故答案为:黄。共三种颜色的粉笔,抽到哪种颜色的粉笔都有可能,哪种颜色的粉笔最多,抽到这种颜色的康乃馨就最大。
21.109.5;74.25
解:(5.5×4.5+3×4.5 +5.5×3) ×2(24.75+13.5 +16.5)×2= 54.75×2= 109.5(平方厘米)
5.5×4.5×3=24×3= 74.25(立方厘米)
故答案为:109.5;74.25
长方体的表面积=(长×宽+长×高+宽×高)×2 。长方体的体积=长×宽×高
22.长方;2+4ah;圆柱;6.28
解:(a×a+a×h+a×h)×2=(+2ah)×2=2+4ah
左边一个是长方体,表面积是2+4ah;
3.14×1×1×2=6.28(立方厘米)
右边一个是圆柱体,体积是6.28立方厘米。
故答案为:长方;2+4ah;圆柱;6.28。
(长×宽+长×高+宽×高)×2=长方体的表面积;π×底面半径的平方×高=圆柱的体积。
23.16;10;80;八
解:4:5===;;4:5=0.8=80%=八折。
故答案为:16;10;80;八。
比的前项相当于分数的分子,后项相当于分母。根据分数与比的关系结合分数的基本性质确定分子或分母。用前项除以后项求出比值,再化成百分数;根据百分数确定折扣即可。
24.150.72;125.6
25.45;15
26.1695.6
解:169.56÷4=42.39(cm2),4dm=40cm,体积:42.39×40=1695.6(cm3)。
故答案为:1695.6。
把3个相同的圆柱拼成一个大圆柱,表面积会比原来3个小圆柱的表面积之和减少了4个底面的面积,因此用表面积减少的部分除以4求出底面积,再用底面积乘大圆柱的高即可求出大圆柱的体积。注意统一单位。
27.慈利县;7
28.0.5
解:2.5cm=25mm,25÷50=0.5(mm)。
故答案为:0.5。
50:1的意思就是图上距离是实际距离的50倍,所以用图上距离除以50即可求出实际距离。注意换算单位。
29.(1)48;56
(2)12
解:(1)甲的体重为50+4=54(kg),乙的体重为50-8=42(kg),丁的体重为50-2=48(kg)
甲、乙、丙、丁四人的体重和=50×4=200(kg),甲、乙、丁三人的体重和为54+42+48=144(kg),所以丙的体重为200-144=56(kg);
(2)已知甲的体重为54kg,乙的体重为42kg,所以甲的体重比乙体重重54-42=12(kg)。
故答案为:(1)48;56(2)12。
(1)观察条形图得出甲、乙、丁三人的体重,进而根据平均体重=,得出丙的体重;
(2)用甲的体重减去乙的体重即为甲的体重比乙体重重的千克数。
30.20;24;60;六
解:=(3×4):(5×4)=12:20;
=(3×8)÷(5×8)=24÷40;
=3÷5=0.6=60%=六成;
所以12:20==24÷40=60%=六成。
故答案为:20;24;60;六。
比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变;分数化成百分数,用分数的分子除以分母化成小数,然后把小数的小数点向右移动两位,再加上百分号;百分之几十就等于几成。
31.(1)正
(2)20
32.200
解:10÷5%=200(万元)
故答案为:200。
税率是缴纳的税额与营业额的比率,用缴纳的营业税除以税率即可求出该月的营业额。
33.;0.016
解:三角形ADP的面积=×DP×高,平行四边形ABCP的面积=PC×高,三角形ADP的高与平行四边形ABCP的高相等;
又因为DP:PC=2:3,根据比例的基本性质,得到2PC=3DP,故PC=DP,平行四边形ABCP的面积=DP×高;
==×=,故三角形ADP的面积是平行四边形ABCP的;
已知平行四边形ABCP的面积是120 cm2,所以三角形ADP的面积=平行四边形ABCP的面积=×120=40(cm2);
梯形面积=120+40=160(cm2)=0.016(cm2)。
故答案为:;0.016。
根据面积公式:三角形面积=×底×高,平行四边形面积=底×高,以及比例的基本性质:外项积等于内项积,列出关于三角形和平行四边形面积的式子,两个式子作比即可求出三角形ADP的面积是平行四边形ABCP的多少;
梯形面积=三角形面积=平行四边形面积,根据第一空所得的三角形ADP的面积是平行四边形ABCP的面积的关系,以及题干中告诉的平行四边形的面积求出三角形的面积,进而求出梯形ABCD的面积,并将所求面积单位平方厘米换算成题干中的平方米。
34.1∶200
35.16;48
36.
解:64:27=:,
两个正方体的体积比是64:27,两个正方体的棱长比是4:3,
3÷4=,小正方体的棱长是大正方体棱长的。
故答案为:。
正方体的体积=棱长×棱长×棱长,小正方体的棱长÷大正方体的棱长=小正方体的棱长是大正方体棱长的几分之几。
37.3;18.84;9.42
解:圆柱的高是3cm;侧面积:6.28×3=18.84(cm2);底面半径:6.28÷3.14÷2=1(cm),体积:3.14×12×3=9.42(cm3)。
故答案为:3;18.84;9.42。
根据图形可知,6.28cm是底面周长,高是3cm。用底面周长乘高求出侧面积。用底面周长除以3.14再除以2求出底面半径,然后用底面积乘高求出体积即可。
38.2.86
39.5;4;25;16;二五
解:二成五=25%;20×25%=5;4÷25%=16;所以5:20==25%=4÷16=二五折=二成五。
故答案为:5;4;25;16;二五。
二成五就是25%。用后项乘25%求出前项;用被除数除以25%求出除数;把25%写成分母是100的分数并化成最简分数;根据百分数确定折扣即可。
40.86;-5.5
41.282.6;60
解:3.14 × (6 ÷2)2×10=3.14×9×10=28.26×10= 282.6(立方厘米)
底面半径:6÷2=3(厘米)10×3 ×2=30×2=60(平方厘米)
故答案为:282.6;60
根据圆柱体积公式的推导过程可知:把圆柱切拼成一个近似长方体后体积不变。拼成的长方体的表面积把圆柱的表面积增加了两个切面的面积,根据圆柱的体积公式:V= πr2h,长方形的面积公式:S =ab,把数据代入公式解答。
42.300;
解:实际距离==厘米=千米。实际距离,即,简化比例尺为。
故答案为:300;
图上距离:实际距离=比例尺,据此回答即可。
43.(1)二百五十一亿九千万;252
(2)12
解:(1)横线上的数25190000000读作二百五十一亿九千万,省略亿位后面的尾数,约是252亿元。
(2)60千米=6000000厘米
6000000×=12(厘米)
把城际铁路全长画在一张比例尺为1∶500000的地图上,图上距离是12厘米。
故答案为:二百五十一亿九千万;252;12。
(1)要读亿以上数, 亿以上的数的读法:先分级,再从高位读起,读完亿级或万级的数,要加上”亿“字或”万“字,每级末尾不管有几个0都不读,其他数位有一个0或连续几个0,都只读一个0。
改写成用“亿”作单位的数,小数点向左移动8位,再在后面加上一个“亿”字,注意要用四舍五入舍去亿后面的数字。
(2)先把60千米化为6000000厘米,再根据图上距离=实际距离×比例尺,求出60千米的图上距离。
(1)25190000000读作二百五十一亿九千万,省略亿位后面的尾数,约是252亿元。
(2)60千米=6000000厘米
6000000×=12(厘米)
把城际铁路全长画在一张比例尺为1∶500000的地图上,图上距离是12厘米。
44.18.84;28.26平方分米
45.9
46.20∶1
47.3
48.471
49.216;243
50.36;12
同课章节目录
