2024-2025学年苏教版六年级数学下册期末真题汇编专练04-解答题2(含答案+解析)
文档属性
| 名称 | 2024-2025学年苏教版六年级数学下册期末真题汇编专练04-解答题2(含答案+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-26 16:52:27 | ||
图片预览




文档简介
2024-2025学年苏教版六年级数学下册期末真题汇编
专练04-解答题2
一、解决问题
1.(2024六下·海安期末)6分)一个无盖的长方体玻璃鱼缸,长10分米,宽6分米,高7分米。
(1)做这个鱼缸至少需要玻璃多少平方分米?
(2)若往鱼缸里放入330升水,水面离缸口多少分米?
2.(2024六下·安源期末)一个圆柱形的玻璃缸装有一些水,底面内直径为6cm,高为12cm。把一个圆锥形铅锤放入玻璃缸中(全部浸没),水面上升了0.5cm,铅锤的高为2cm,这个铅锤的底面积是多少平方厘米?
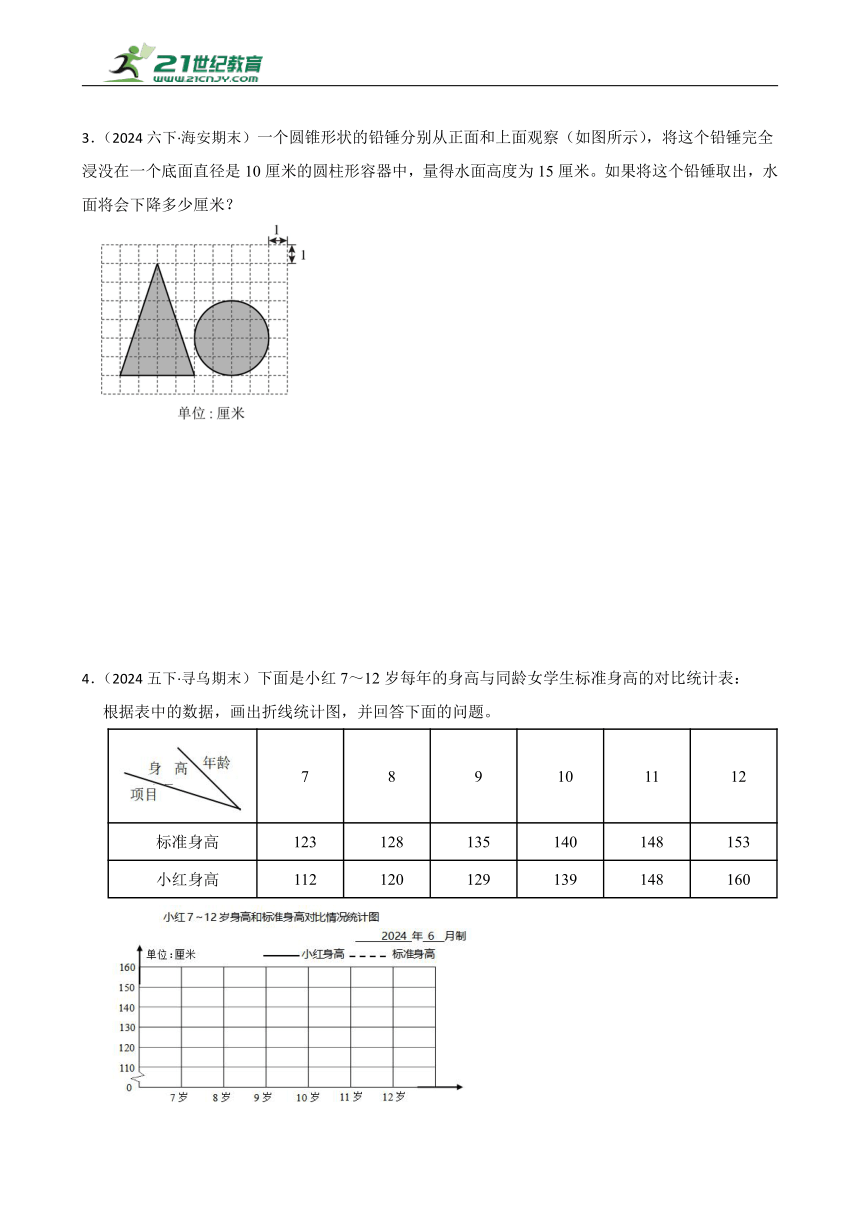
3.(2024六下·海安期末)一个圆锥形状的铅锤分别从正面和上面观察(如图所示),将这个铅锤完全浸没在一个底面直径是10厘米的圆柱形容器中,量得水面高度为15厘米。如果将这个铅锤取出,水面将会下降多少厘米?
4.(2024五下·寻乌期末)下面是小红7~12岁每年的身高与同龄女学生标准身高的对比统计表:
根据表中的数据,画出折线统计图,并回答下面的问题。
7 8 9 10 11 12
标准身高 123 128 135 140 148 153
小红身高 112 120 129 139 148 160
(1)根据表中的数据,画出折线统计图。
(2)小红从 岁到 岁身高增长得最快。
(3)对比标准身高,说说你对小红7~12岁身高增长情况的看法?
5.(2024六下·安源期末)一列火车以每小时140千米的速度从甲地开往乙地,3小时行驶了全程的,那么在比例尺是1:7000000的地图上,甲、乙两地之间铁路线的长为多少?
6.(2024六下·南山期末)一分钟踢键子决赛,前3名选手的前三轮成绩如下表所示。
姓名 第一轮个数 第二轮个数 第三轮个数 平均成绩
淘气 25 50 36
笑笑 45 48 30
妙想 40 41 45
(1)按平均分排名,谁获得第一名?
(2)按单轮成绩最高排名,谁获得第一名?
(3)实际结果笑笑是本次冠军,你猜本次比赛按什么规则排名?并分析这个规则的优缺点。
7.(2024六下·龙华期末)木工师傅用正方体木块切割加工圆柱体。正方体木块棱长是12厘米。请分别解决以下问题。(此题结果可用含π的式子表示,也可将π取3.14计算。)
(1)如果用这个正方体木块切割出一个最大的圆体,如图1,这个圆柱体的体积是多少?被切割掉的边角料的体积是多少?
(2)如果用这个正方体木块切割出4个大小相等且体积最大的圆柱体,如图2,每个小圆柱体的体积是多少?被切割掉的边角料的体积是多少?
(3)如果继续像上面这样加工圆柱体,加工9个大小相等且体积最大的圆柱体,被切割掉的边角料的体积是多少?
(4)奇思在解决上述问题时,他发现被切割出来的圆柱体的个数是1×1,2×2,3×3,……,n×n。那么,当被切割出来的圆柱体的个数是n×n时,每个小圆柱体的半径是⑵厘米,每个小圆柱体的体积是⑵立方厘米。按照这种想法,此时,被切割掉的边角料体积是多少?你发现了什么?
8.(2024六下·大冶期末)某银行经理给张叔叔推荐办一张借贷卡,介绍说“1万元每天利息只要1.35元”。(1年按365天计算)
(1)如果张叔叔用这张卡借贷10万元,一年的贷款利息是多少元
(2)这张借贷卡的贷款年利率是多少 (百分数保留一位小数)
9.(2024六下·黄石期末)星星小学六年级有350人,视力情况如下图。
(1)假性近视的有多少人
(2)六年级视力不良(包括假性近视和近视)的人数比视力正常的人数多总人数的百分之几?
10.(2024六下·黄石期末) 一个车间装配一批电视机,如果每天装50台,60天可以完成任务。如果要提前20天完成任务,每天至少应装多少台 (用比例解)
11.(2024六下·杭州期末)某小学建一个长方体游泳池,长80米,宽25米,深2米。
(1)在游泳池的底部和四周贴瓷砖,贴瓷砖的面积有多少平方米?
(2)如果在游泳池内注水到1.2米的高度,那么需要注入多少立方米的水?
12.(2024六下·南山期末)正六边形的边长为4厘米,六个圆形的圆心分别在六边形的顶点上。如果小圆的半径为1厘米,求浅灰色部分与涂色部分面积之比。
13.(2024六下·黄石期末) 一辆货车车厢是一个长方体,它的长是6米,宽是1.5米,高是3米。装一车沙子,卸下后沙子堆成一个高是2米的圆锥体,这个沙堆的底面积是多少平方米
14.(2024·绵阳)如图,在一个圆形时钟的表面上,OA表示时针,OB表示分针(O为两针的旋转中心),下午3点时,OA与OB成直角。
(1)分针每分针为 度,时针每分钟转 度;
(2)3:15时,时针与分针所成的角度是 。
(3)在下午3点至4点之间,从下午3点开始,经过 分钟,时针与分针成60°角。
15.(2024六下·瑞安期末)请你结合以下3幅统计图中的信息解决问题。
(1)明明家4月份总支出是 元。
(2)请把条形统计图中“食品”类的直条补充完整。
(3)国际上通常用食品支出占家庭总支出的百分比(即恩格尔系数)来衡量一个国家的人民生活水平。参照下表的恩格尔系数,你觉得明明家处于 生活水平。
恩格尔系数 大于 60% 50%~60% 40%~50% 30%~40% 20%~36% 20%以下
生活水平 贫穷 温饱 小康 相对富裕 富裕 极其富裕
(4)人们都说“近 20年,温州城镇和农村居民的生活水平越来越好。”请结合图表进行数据说明,分析理由。
16.(2024·绵阳)超市推出如下优惠:
⑴一次性购物不超过100元,不享受优惠;
⑵一次性购物超过100元,但不超过300元一律9折;
⑶一次性购物超过300元,一律8折;
两次购物分别付款80元,252元。若一次性购买则应付款多少元?
17.(2024六下·长沙期末)为庆祝“六一”儿童节,学校举办了一场趣味运动会。后勤处共采购了8大箱奖励物资,每箱原价400元。因正遇商家店庆。所有商品一律九折。后勤处购买这批物资实际花了多少钱
18.(2024六下·双流期末)某市大力发展新能源,建造了各种新能源发电厂
某市新能源发电厂投入资金与发电量统计表
类型 风力发电 太阳能发电 水力发电
投入/亿元 8
发电量/亿度 0.8 0.7 1.5
(1)分别求出“风力发电”和“太阳能发电”的投入资金,填入上面表中。
(2)已知这三类新能源发电盘占该地区总发电量的25%,求该地区的总发电量。
19.(2024六下·双流期末)“丝绸之路”是古代连接中西方的商道。传统的丝绸之路起自我国古代都城长安,直延伸到欧洲,在一幅比例尺为1:8000000的地图上约长85厘米,传统的丝绸之路实际全长约为多少千米?
20.(2024六下·双流期末)一台压路机的前轮是圆柱形,轮宽3米,直径1米。压路机前轮转动5周,压路的面积是多少平方米?
21.(2024·钱塘期末)钱塘小学开展阳光体育运动,调查了六年级男生最喜欢的球类运动项目,并将调查情况制成如下统计表和统计图。
(1)将统计表和统计图中的数据补充完整。
项目 排球 篮球 足球 其他
人数 30 30
(2)已知其他球类项目中,有60%的男生最喜欢乒乓球,最喜欢网球的人数与最喜欢乒乓球的人数的比是1∶3,最喜欢网球的有多少人?
22.(2024五下·寻乌期末)黄师傅要做一个长15厘米,宽10厘米,高200厘米的长方体烟囱,至少需要多少平方厘米的铁皮?
23.(2024五下·寻乌期末)在一个长为80厘米,宽为40厘米的玻璃缸中,放入一石块,石块浸没水中,这时水深为30厘米,取出石块后水深为25厘米,这块石块的体积是多少立方分米?
24.(2024六下·黄石期末)张爷爷将50000元存入银行,定期二年,年利率为2.5%。到期后,张爷爷将所得利息捐给了希望工程,他捐出了多少钱
25.(2024五下·寻乌期末)王阿姨今天给月季和君子兰同时浇水,月季每4天浇一次水,君子兰每6天浇一次水,至少多少天后给这两种花同时浇水?
26.(2024六下·重庆市期末)下面是三个图形的旋转。
(1)图②中长方形绕一条边旋转一周,得到图形的体积,是图①中直角三角形绕直角边旋转一周,得到图形体积的 倍。并请说明理由 。
(2)图③中平行四边形绕AB 边旋转一周,得到图形的体积是多少cm3?
27.(2024六下·临平期末)太空育种是当今世界农业领域的尖端科学技术,世界上仅有三个国家拥有该技术,我国就是其中之一。为选取优质小麦种子进行太空培育,某种子基地用A、B、C三种型号的种子进行发芽实验,实验种子数量及发芽情况如下图。
(1)参加发芽实验的三种型号小麦种子共2000粒,其中B型号种子的发芽率是95%,B型号种子的发芽数是 粒。
(2)请将扇形统计图和条形统计图补充完整。
(3)根据实验数据,你建议选取哪种型号的种子进行太空培育比较合适?请说明理由。
28.(2024六下·临平期末)下图中的容器由1个大圆柱和1个小圆柱组成,如果向这个容器匀速注满油,注油过程中,容器中油的高度与所用时间的关系如下图所示。
(1)把下面的大圆柱注满需要 分钟。
(2)上面小圆柱高 厘米。
(3)如果下面大圆柱的底面积是48平方厘米,那么上面小圆柱的底面积是多少?
29.(2024六下·临平期末)只列算式,不计算。
(1)沈叔叔将50000元钱存入银行,整存整取2年。如果年利率是2.2%,到期可取回本金与利息一共多少元?
算式:
(2)一辆变速自行车前齿轮有2个(齿数为48和36),后齿轮有3个(数为20、16和12),这辆自行车的车轮直径是0.7米,蹬一圈,最远能蹬出的距离是多少米?
算式:
30.(2024六下·泗洪期末)李师傅向右图所示的空容器(由上、下两个圆柱组成)中均匀注油,正好注满。注油过程中,容器中油的高度与所用时间的关系如图所示。
(1)把下面的大圆柱注满需 分钟。
(2)上面小圆柱高 厘米。
(3)如果下面的大圆柱的底面积是48平方厘米,那么大圆柱的体积是多少立方厘米?上面小圆柱的底面积是多少平方厘米?(写出计算过程)
31.(2024六下·渝中期末)一个密闭玻璃容器是由一个圆柱和一个圆锥组成的,里面装有一些水(如图1,单位:dm,玻璃厚度忽略不计)。
(1)容器的占地面积是多少平方分米?
(2)容器中水的体积是多少立方分米?
(3)如果将这个容器倒过来(如图2),从水面到圆锥顶点的高度是多少分米?
(2024六下·渝中期末)只列综合算式或方程,不计算。
32.小明爸爸得到一笔 3000 元的劳务报酬,其中 800元是免税,其余部分要按20%的税率缴税。这笔劳务报酬一共要缴税多少元?
33.今年“五·一”期间,解放碑商圈日均迎客约 90万人次,日均客流量比去年同期增长,去年日均客流量为多少万人次?
34.实验小学开展“以纸换树、保护环境”的活动,共回收1.8t 废纸。据统计,每回收 5t废纸进行再利用,相当于保护了 85棵树。实验小学回收的废纸进行再利用,相当于保护了多少棵树?
35.一个零件由两个圆柱组成(如图),它们的高都是10cm,底面半径分别是4cm和8cm。现在要给这个零件的表面涂上颜色,涂色部分共多少 cm2?
36.(2023六下·石城期末)如图所示,有一块长方形铁皮,把其中的阴影部分剪下制成一个圆柱形油桶。(接口处忽略不计)
(1)圆柱形油桶的表面积是多少平方分米?
(2)圆柱形油桶的体积是多少立方分米?
37.(2024六下·越秀期末) 一项工程,若每天工作8小时,则15天可以完成任务。要想12天完成任务,平均每天要工作多少小时 (用比例知识列方程解答)
38.(2024六下·麻城期末)农场在地面上挖了一个圆柱形蓄水池,它的底面周长是125.6米,深是20分米,把底面和侧面抹上水泥,需要抹水泥的面积有多少平方米?这个水池能蓄水多少立方米?
答案解析部分
1.(1)解:10×6+10×7×2+6×7×2
=60+140+84
=284(平方分米)
答:做这个鱼缸至少需要玻璃284平方分米。
(2)解:330升=330立方分米
330÷(10×6)
=330÷60
=5.5(分米)
7﹣5.5=1.5(分米)
答:水面离缸口1.5分米。
(1)长方体的长×宽+长×高×2+宽×高×2=无盖的长方体的表面积;
(2)水的体积÷长方体的底面积=水的高度,长方体的高-水的高度=水面离缸口的高度。
2.解:3.14×(6÷2)2×0.5×3÷2
=3.14×9×0.5×3÷2
=42.39÷2
=21.195(平方厘米)
答:这个铅锤的底面积是21.195平方厘米。
水面升高部分水的体积就是铅锤的体积,因此用玻璃缸的底面积乘水面上升的高低即可求出铅锤的体积。根据圆锥的体积公式,用铅锤的体积乘3再除以高即可求出底面积。
3.解:从图中可以看出,圆锥的高是6厘米,底面半径是2厘米,
圆锥的体积:3.14×2×2×6÷3
=12.56×6÷3
=25.12(立方厘米)
圆柱的底面半径:10÷2=5(厘米)
25.12×3÷(3.14×5×5)
=75.36÷78.5
=0.96(厘米)
答:水面将会下降0.96厘米。
π×底面半径的平方×高÷3=圆锥的体积;圆锥的体积×3÷圆柱的底面积=水面将会下降的高度。
4.(1)
(2)11;12
(3)小红11岁以前不到标准身,可能是缺乏锻炼,挑吃造成的。
(1)根据统计表 的数据描点、连线。
(2)7至8岁增长8厘米,8至9岁增长9厘米,9至10岁增长10厘米,10至11岁增长厘米,11至12岁增长12厘米,所以11岁到12岁增长最快、
(2)主观题,根据图表回答。
5.解:140×3÷
=420÷
=980(千米)
980千米=98000000厘米
98000000×=14(厘米)
答:甲、乙两地之间铁路线的长为14厘米。
用速度乘3求出3小时行驶的路程,根据分数除法的意义,用3小时行驶的路程除以求出全程。把全程换算成厘米,然后用实际距离乘比例尺即可求出图上距离。
6.(1)解:淘气:(25+50+36)÷3=111÷3=37(个)
笑笑:(45+48+30)÷3=123÷3=41(个)
妙想:(40+41+45)÷3=126÷3=42(个)
37<41<42
答:妙想获得第一名。
(2)答:单论最高成绩是50个,所以淘气会获得第一名。
(3)解:按单轮成绩最高排名,淘气获得第一名;
按第一轮成绩排名:25个<40个<45个,笑笑获得第一名;
按第二轮成绩排名:41<48<50,淘气获得第一名;
按第三轮成绩排名:30个<36个<45个,妙想获得第一名;
由此可知:笑笑是本次冠军,是按第一轮的成绩进行排名的。
优点:规则简便容易操作,缺点:不能准确反映三人的真实水平。
(1)先根据“平均数=数据和÷数据个数”,求出三人的平均成绩,再比较大小即可;
(2)分别比较出三轮成绩中9个数字的大小,看谁的单轮成绩最高即可;
(3)先确定是根据平均数还是单轮成绩确定了笑笑是本次冠军,然后分析这个规则的优缺点即可。
7.(1)解:3.14×(12÷2)2×12
=3.14×432
=1356.48(立方厘米)
12×12×12=1728(立方厘米)
1728-1356.48=371.52(立方厘米)
答:这个圆柱的体积是1356.48立方厘米,被切割掉的边角料的体积是371.52立方厘米。
(2)解:3.14×(12÷2÷2)2×12
=3.14×108
=339.12(立方厘米)
1728-339.12×4
=1728-1356.48
=371.52(立方厘米)
答:每个小圆柱的体积是339.12立方厘米,被切割掉的边角料的体积是371.52立方厘米。
(3)解:1728-3.14×(12÷3÷2)2×12×9
=1728-3.14×432
=1728-1356.48
=371.52(立方厘米)
答:被切割的边角料的体积是371.52立方厘米。
(4)答:当被切割出来的圆柱体的个数是n×n时,每个小圆柱体的半径是(12÷n÷2)厘米,每个小圆柱体的体积是(1356.48÷n2)立方厘米。按照这种想法,此时,被切割掉的边角料体积是371.52立方厘米,我发现,被切割掉的边角料的体积是不变的。
(1)这个最大的圆柱的底面直径和高都与正方体的棱长相等,确定圆柱的底面直径和高,用底面积乘高求出圆柱的体积。用正方体的体积减去圆柱的体积求出被切割掉的边角料的体积;
(2)切割出4个大小相等的圆柱,底面半径是(12÷2÷2)厘米,高是12厘米,由此求出一个圆柱的体积。用正方体的体积减去4个这样的圆柱的体积即可求出边角料的体积。
(3)切割出9个大小相等且体积最大的圆柱,底面直径是(12÷3÷2)厘米,高是12厘米,先计算出一个圆柱的体积,然后用正方体的体积减去9个圆柱的体积就是被切割掉的边角料的体积;
(4)用正方体的棱长除以n再除以2求出切割后每个小圆柱的底面半径。切割出的所有圆柱的体积和是不变的,所以用体积和除以n2即可表示出每个小圆柱的体积。每种切割方法下边角料的体积都是不变的。
8.(1)解:10×1.35×365
=13.5×365
=4927.5(元)
答:一年的贷款利息是4927.5元。
(2)解:4927.5÷10000÷1≈4.9%
答:这张借贷卡的贷款年利率是4.9%。
(1)一年的贷款利息=张叔叔借款金额×平均每天的利息×天数;
(2)这张借贷卡的贷款年利率=利息÷本金÷时间。
9.(1)解:350×(1-28%-42%)
=350×30%
=105(人)
答:假性近视的有105人。
(2)解:350×42%=147(人)
350-147=203(人)
(203-147)÷147
=56÷147
≈38.1%
答:六年级视力不良(包括假性近视和近视)的人数比视力正常的人数多总人数的38.1%。
(1)假性近视的人数=星星小学六年级总人数×(1-其余各项分别占的百分率);
(2)六年级视力不良(包括假性近视和近视)的人数比视力正常的人数多总人数的百分率=(六年级视力不良的人数-视力正常的人数)÷视力正常的人数。
10.解:设每天至少应装x台。
(60-20)x=50×60
40x=3000
x=3000÷40
x=75
答:每天至少应装75台。
设每天至少应装x台。依据(计划的天数-提前的天数)×实际平均每天至少装的台数=计划的天数×计划平均每天装的台数,列比例,解比例。
11.(1)解:80×25+2×(80×2+25×2)
=80×25+2×210
=2000+420
=2420(m2)
答:贴瓷砖的面积为2420(m2)。
(2)解:80×25×1.2
=2000×1.2
=2400(m3)
答:需要注入 2400m3的水。
(1)贴瓷砖的面积=长×宽+(长×高+宽×高)×2;
(2)需要注入水的体积=游泳池的长×宽×水面的高度。
12.解:浅灰色部分的面积=一个小圆的面积+一个大圆的面积,
深灰色部分面积=2个小圆的面积+2个大圆的面积=2×(一个小圆的面积+一个大圆的面积)=2×浅灰色部分的面积;
所以浅灰色部分与深灰色部分面积之比是1:2。
正六边形的内角和是720度,相当于两个圆的内角和,所以浅灰色部分的面积=一个小圆的面积+一个大圆的面积;那么外面深灰色部分面积=2个小圆的面积+2个大圆的面积;即外面深灰色部分面积=2×(一个小圆的面积+一个大圆的面积);由此确定浅灰色部分与深灰色部分的面积比即可。
13.解:6×1.5×3×3÷2
=27×3÷2
=81÷2
=40.5(平方米)
答:这个沙堆的底面积是40.5平方米。
这个沙堆的底面积=长方体车厢的长×宽×高×3÷圆锥的高。
14.(1)6;0.5
(2)7.5°
(3)或
解:(1)分针每分钟转:360°÷60=6°,时针每分钟转30°÷60=0.5°;
(2)0.5×15=7.5°;
(3)当分针在时针上方时:
(90-60)÷(6-0.5)
=30÷5.5
=(分钟)
当分针在时针下方时:
(90+60)÷(6-0.5)
=150÷5.5
=(分钟)
故答案为:(1)6;0.5;(2)7.5°;(3)或。
(1)分针走1圈是60分,一圈是360°,所以用360除以60就是分针每分钟转的度数。时针走1大格是60分,一大格是30°,所以用30除以60即可求出时针每分钟走的度数;
(2)3:15,分针指向3,时针超过3,因此只需要计算时针15分钟走的度数就是两针之间夹角的度数;
(3)要分两种情况考虑,根据追及问题解答。第一种情况:分针在时针的上面,也就是分针没有追上时针。原来两针之间夹角是90°,现在是60°,说明分针追时针了(90-60),用追及度数除以每分钟追的度数即可求出经过的时间。第二种情况,分针超过时针,也就是先追上90°,再超过时针60°,这样分针追了(90+60),用追的度数除以每分钟追的度数即可求出经过的时间。
15.(1)12000
(2)解:12000×(1-30%-10%-35%)
=12000×0.25
=3000(元)
(3)富裕
(4)解:从第三个图可以看出,近20年,恩格尔系数越来越小,说明温州城镇和农村居民的生活水平越来越好。
解:(1)1200÷10%=12000(元)
明明家4月份总支出是12000元。
(3)1-30%-10%-35%=25%
25%在20%~36%之间,属于富裕。
故答案为:(1)12000;(3)富裕。
(1)服装的支出÷服装的支出占总支出的百分率=总支出;
(2)总支出×食品的支出占总支出的百分率=食品的支出,据此作图;
(3)单位1-教育服装其它分别占的百分比=食品占的百分比,据此解答;
(4)答案不唯一,合理即可。
16.解:一次性购物超过100元,但不超过300元一律9折则在这个范围内最低付款90元,因而第一次付款80元,没有优惠;
第二次购物时:是第二种优惠,可得出原价是 252÷90%=280(符合超过100不高于300);
则两次共付款:80+280=360元,超过300元,则一次性购买应付款:360×080%=288元;
当第二次付款是超过300元时:可得出原价是 252÷080%=315(符合超过300元),
则两次共应付款:80+315=395元,则一次性购买应付款:395×80%=316元。
答:则一次性购买应付款288元或316元。
第一次购物的80元是没有优惠的。第二次购物的252元分两种情况,也就是可能享受的九折优惠,也可能销售的八折优惠。由此分两种情况计算出第二次购物的原价,进而分两种情况计算一次性购物应付的钱数即可。
17.解:400×90%×8
=360×8
=2880(元)
答:后勤处购买这批物资实际花了2880元。
每箱原价×折扣=每箱的现价,每箱的现价×买的箱数=一共花的钱数。
18.(1)解:8÷50%=16(亿元),
太阳能发电:16×20%=3.2(亿元),
风力发电:16×30%=4.8(亿元),
如下表所示:
类型 风力发电 太阳能发电 水力发电
投入/亿元 4.8 3.2 8
发电量/亿度 0.8 0.7 1.5
(2)解:(0.8+0.7+1.5)÷25%
=3÷25%
=12(亿度)
答:该地区的总发电量12亿度。
(1)根据资金与发电量统计表可知水力发电投入资金为8亿元,根据扇形统计图可知水力发电投入资金占该市新能源发电投入资金的50%,根据已知一个数的百分之几是多少,求这个数,用除法计算,用水力发电投入的资金除以水力发电投入资金占该市新能源发电投入资金的百分数即可求出该市投入新能源发电厂的资金;根据求一个数的已分之几是多少,用乘法计算,用该市投入新能源发电的资金乘太阳能发电和风力发电占该市投入新能源发电资金的百分数即可求出太阳能发电和风力发电投入的资金;
(2)根据(1)可知三种新能源发电的度数,根据加法意义,把风力发电、太阳能发电、水力发电的度数之和相加求和即可求出该市新能源发电的度数之和,根据已知一个数的百分之几是多少,求这个数,用除法计算,用新能源发电的度数之和除以三类新能源发电量占该地区总发电量的百分数即可求出该地区的总发电量。
19.解:88÷= 704000000(厘米),
704000000厘米=7040千米;
答:传统的丝绸之路实际全长约为7040千米。
根据比例尺=图上距离÷实际距离,实际距离=图上距离÷比例尺,据此求解。
20.解:轮宽看做圆柱的高,
3.14×1×3×5
=9.42×5
=47.1(平方米)
答:压路的面积是47.1平方米。
压路机的前轮转动一圈压路的面积就是圆柱的侧面积,π×直径=底面周长,底面周长×高=侧面积,侧面积×5=转动5周压路的面积。
21.(1)解:1-25%-25%-12.5=37.5%
30÷25%=120(人)
120×37.5%=45(人)
120×12.5%=15(人)
项目 排球 篮球 足球 其他
人数 30 30 45 15
(2)解:15×60%=9(人)
9÷3=3(人)
答:最喜欢网球的有3人。
(1)排球占25%,足球占的分率=1-其余各项分别占的百分率;
喜欢足球的人数=总人数×喜欢足球占的分率;其中,总人数=喜欢篮球的人数÷喜欢篮球占的分率;
喜欢其他的人数=总人数×喜欢其他占的分率,然后填写统计表和统计图;
(2)最喜欢网球的人数=最喜欢乒乓球的人数÷3,其中,最喜欢乒乓球的人数=喜欢其他的人数×60%。
22.解:(10×200+15×200)×2
=5000×2
=10000(平方厘米)
答:至少需要10000平方厘米的铁皮。
制做长方体烟囱,至少需要多少平方厘米的铁皮,只需要求前后左右4个面的面积。
23.解:80×40×(30-25)
=3200×5
=16000(平方厘米)
=16(立方分米)
答:这块石块的体积是16立方分米。
排水法求不规则物体的体积,石块浸没在水中,水上升(下降)的体积就是不规则物体的体积。
24.解:50000×2×2.5%
=100000×2.5%
=2500(元)
答:他捐了2500元。
张爷爷捐的钱数=所得利息,其中,利息=本金×利率×存期。
25.解:月季每4天浇一次水,浇水时间是第4、8、12、16、20、24……
君子兰每6天浇一次水,浇水时间是第6、12、18、24……
共同浇水时间是12、24……
答:至少12天后给这两种花同时浇水。
根据题意,月季每4天浇一次水,君子兰每6天浇一次水,那么每4和6的最小公倍数天后两种花同时浇水,据此解答。
26.(1)3;因为等底等高的圆柱的体积是圆锥体积的3倍
(2)解:3.14×4×4×3
=50.24×3
=150.72(立方厘米)
答:得到图形的体积是150.72立方厘米。
解:(1)图②中长方形绕一条边旋转一周,得到图形的体积,是图①中直角三角形绕直角边旋转一周,得到图形体积的3倍,因为等底等高的圆柱的体积是圆锥体积的3倍。
故答案为:(1)3;因为等底等高的圆柱的体积是圆锥体积的3倍。
图③中平行四边形绕AB 边旋转一周,得到图形的体积=圆柱的体积=π×半径×半径×高。
27.(1)665
(2)解:1-35%-35%=30%
(3)解:644÷(2000×35%)
=644÷700
=92%
518÷(2000×30%)
=518÷600
≈86.33
95%>93%>86.33%
答:建议选取B种型号的种子进行太空培育比较合适,因为这种的发芽率高。
解:(1)2000×35%×95%
=700×95%
=665(粒)。
故答案为:(1)665。
(1)B型号种子的发芽数=参加发芽实验的三种型号小麦种总粒数×B占的分率×B型号种子的发芽率;
(2)C占的百分率=1-其余各项分别占的百分率;画出直条,并且标上数据;
(3)发芽率=A、C分别发芽的种子粒数÷(参加发芽实验总粒数×各自分别占的百分率),然后比较大小,要选择发芽率高的种子。
28.(1)8
(2)30
(3)解:48×20÷8
=960÷8
=120(立方厘米)
120×(12-8)÷30
=480÷30
=16(平方厘米)
答:上面小圆柱的底面积是16平方厘米。
解:(1)把下面的大圆柱注满需要8分钟;
(2)50-20=30(厘米),上面小圆柱高30厘米。
故答案为:(1)8;(2)30。
(1)观察统计图可知:把下面的大圆柱注满需要8分钟;
(2)上面小圆柱的高=总高度-大圆柱的高;
(3)平均每分钟注水的体积=大圆柱的体积÷大圆柱注满水需要的时间,其中,大圆柱的体积=底面积×大圆柱的高,上面小圆柱的底面积= 平均每分钟注水的体积×(12-8)÷小圆柱的高。
29.(1)解:50000×2×2.2%+50000
(2)解:3.14×0.7×(48÷12)
(1)到期可取回本金与利息总钱数=本金+利息,其中,利息=本金×利率×存期;
(2)最远能蹬出的距离=π×直径×蹬一圈自行车走的圈数;其中,蹬一圈自行车走的圈数=48÷12。
30.(1)1
(2)30
(3)解:48×20=960(立方厘米)
960÷1=720(立方厘米)
720×=480(立方厘米)
480÷30=16(平方厘米)
答:上面小圆柱的底面积是16平方厘米。
解:(1)1+1÷3=1+=1(分)
把下面的大圆柱注满需1分钟。
(2)50-20=30(厘米)
上面小圆柱高30厘米。
故答案为:(1)1;(2)30。
(1)1分钟背平均分成3份,1份是分钟,据此解答;
(2)20~50之间的长度就是小圆柱的高;
(3)大圆柱的底面积×大圆柱的高=大圆柱的体积,大圆柱的体积÷用的时间=1分钟注入油的体积,1分钟注入油的体积×小圆柱注入的时间=小圆柱的体积,小圆柱的体积÷小圆柱的高=小圆柱的底面积。
31.(1)解:3.14×(9÷2)2
=3.14×4.52
=3.14×20.25
=63.585(平方分米)
答: 容器的占地面积是63.585平方分米。
(2)解:63.585×6=381.51(立方分米 )
答: 容器中水的体积是381.51 立方分米 。
(3)解:(381.51-63.585×6×)÷63.585
=(381.51-381.51×)÷63.585
=(381.51-127.7)÷63.585
=254.34÷63.585
=4(分米)
4+6=10(分米)
答: 从水面到圆锥顶点的高度是10分米。
(1)求容器占地面积,就是求这个容器的底面积,根据圆的面积公式:,代入数据,即可解答。
(2)容器中的水的体积,就是底面直径是9分米,高是6分米的圆柱的体积,根据圆柱的体积公式:V=底面积×高,代入数据,即可解答。
(3)根据圆锥的体积公式:V=底面积×高×,代入数据,求出圆锥部分水的体积;由于水的体积不变,再用原来水的体积一圆锥部分的体积,求出网柱部分水的体积,再根据高=圆柱的体积÷圆柱的底面积,代入数据,求出圆柱部分水的高度,再加上圆锥部分的高度,即可解答。
32.解:(3000-800)×20%
33.解:90÷(1+)
34.解:85÷5×1.8
35.解:2×3.14×4×10+2×3.14×8×10+3.14×82×2
(1)考查的是税率的应用;(2)考查的是分数除法的应用;(3)考查的是正比例的应用;(4)考查的是关于圆柱体的组合体表面积的计算,注意重合部分不涂色。
32.应纳税部分×税率=应纳税额,求他缴纳的税,就是求一个数的百分之几是多少,用乘法计算即可,据此解答。
33.比去年同期增长就是(1+),本题中单位“1”的量“去年同日均客流量”未知,所以用除法计算,据此解答。
34.根据题意知道,每回收5t废纸进行再利用,相当于保护了85棵树。因此,1t废纸进行再利用能保护的树的数量为(85÷5)棵,实验小学回收了1.8t废纸,那么,实验小学回收的废纸进行再利用,相当于保护的树的数量为(85÷5×1.8) 棵。
35.由于大小两个圆柱粘合在一起,所以上面的小圆柱只求侧面积,下面的大圆柱求出表面积,然后合并起来就是需要涂色的面积,根据圆柱的表面积=侧面积+底面积×2;据此把数据代入公式解答。
36.(1)18.84÷3.14=6(分米)
10-6=4(分米)
18.84×4+3.14×(6÷2)2×2
=75.36+3.14×9×2
=75.36+56.52
=131.88(平方分米)
答:圆柱形油桶的表面积是131.88平方分米。
(2)3.14×(6÷2)2×4
=3.14×9×4
=28.26×4
=113.04(立方分米)
答:圆柱形油桶的体积是113.04立方分米。
(1)根据圆柱的表面积=侧面积+底面积×2,首先根据圆的周长公式:C=πd,那么d=C÷π,据此求出圆柱的底面直径,圆柱的高用长方形铁皮的宽减去圆柱的底面直径,然后把数据代入公式解答。
(2)根据圆柱的体积公式:V=,把数据代入公式解答。
37.解:平均每天要工作x小时。
8×15=12x
12x=120
x=120÷12
x=10
答:平均每天要工作10小时。
设平均每天要工作x小时。依据计划工作的时间×计划的天数=实际工作的时间×实际工作的天数,列比例,解比例。
38.解:20分米=2米
125.6÷3.14÷2
=40÷2
=20(米)
125.6×2+3.14×202
=251.2+3.14×400
=251.2+1256
=1507.2(平方米)
3.14×202×2
=3.14×400×2
=1256×2
=2512(立方米)
答:需要抹水泥的面积有1507.2平方米;这个水池能蓄水2512立方米。
抹水泥的面积等于圆柱的侧面积加圆柱的底面积,圆柱的侧面积=底面周长×高,圆柱的底面积=π×半径2;圆柱的容积=π×半径2×高,据此代入数值计算即可。
专练04-解答题2
一、解决问题
1.(2024六下·海安期末)6分)一个无盖的长方体玻璃鱼缸,长10分米,宽6分米,高7分米。
(1)做这个鱼缸至少需要玻璃多少平方分米?
(2)若往鱼缸里放入330升水,水面离缸口多少分米?
2.(2024六下·安源期末)一个圆柱形的玻璃缸装有一些水,底面内直径为6cm,高为12cm。把一个圆锥形铅锤放入玻璃缸中(全部浸没),水面上升了0.5cm,铅锤的高为2cm,这个铅锤的底面积是多少平方厘米?
3.(2024六下·海安期末)一个圆锥形状的铅锤分别从正面和上面观察(如图所示),将这个铅锤完全浸没在一个底面直径是10厘米的圆柱形容器中,量得水面高度为15厘米。如果将这个铅锤取出,水面将会下降多少厘米?
4.(2024五下·寻乌期末)下面是小红7~12岁每年的身高与同龄女学生标准身高的对比统计表:
根据表中的数据,画出折线统计图,并回答下面的问题。
7 8 9 10 11 12
标准身高 123 128 135 140 148 153
小红身高 112 120 129 139 148 160
(1)根据表中的数据,画出折线统计图。
(2)小红从 岁到 岁身高增长得最快。
(3)对比标准身高,说说你对小红7~12岁身高增长情况的看法?
5.(2024六下·安源期末)一列火车以每小时140千米的速度从甲地开往乙地,3小时行驶了全程的,那么在比例尺是1:7000000的地图上,甲、乙两地之间铁路线的长为多少?
6.(2024六下·南山期末)一分钟踢键子决赛,前3名选手的前三轮成绩如下表所示。
姓名 第一轮个数 第二轮个数 第三轮个数 平均成绩
淘气 25 50 36
笑笑 45 48 30
妙想 40 41 45
(1)按平均分排名,谁获得第一名?
(2)按单轮成绩最高排名,谁获得第一名?
(3)实际结果笑笑是本次冠军,你猜本次比赛按什么规则排名?并分析这个规则的优缺点。
7.(2024六下·龙华期末)木工师傅用正方体木块切割加工圆柱体。正方体木块棱长是12厘米。请分别解决以下问题。(此题结果可用含π的式子表示,也可将π取3.14计算。)
(1)如果用这个正方体木块切割出一个最大的圆体,如图1,这个圆柱体的体积是多少?被切割掉的边角料的体积是多少?
(2)如果用这个正方体木块切割出4个大小相等且体积最大的圆柱体,如图2,每个小圆柱体的体积是多少?被切割掉的边角料的体积是多少?
(3)如果继续像上面这样加工圆柱体,加工9个大小相等且体积最大的圆柱体,被切割掉的边角料的体积是多少?
(4)奇思在解决上述问题时,他发现被切割出来的圆柱体的个数是1×1,2×2,3×3,……,n×n。那么,当被切割出来的圆柱体的个数是n×n时,每个小圆柱体的半径是⑵厘米,每个小圆柱体的体积是⑵立方厘米。按照这种想法,此时,被切割掉的边角料体积是多少?你发现了什么?
8.(2024六下·大冶期末)某银行经理给张叔叔推荐办一张借贷卡,介绍说“1万元每天利息只要1.35元”。(1年按365天计算)
(1)如果张叔叔用这张卡借贷10万元,一年的贷款利息是多少元
(2)这张借贷卡的贷款年利率是多少 (百分数保留一位小数)
9.(2024六下·黄石期末)星星小学六年级有350人,视力情况如下图。
(1)假性近视的有多少人
(2)六年级视力不良(包括假性近视和近视)的人数比视力正常的人数多总人数的百分之几?
10.(2024六下·黄石期末) 一个车间装配一批电视机,如果每天装50台,60天可以完成任务。如果要提前20天完成任务,每天至少应装多少台 (用比例解)
11.(2024六下·杭州期末)某小学建一个长方体游泳池,长80米,宽25米,深2米。
(1)在游泳池的底部和四周贴瓷砖,贴瓷砖的面积有多少平方米?
(2)如果在游泳池内注水到1.2米的高度,那么需要注入多少立方米的水?
12.(2024六下·南山期末)正六边形的边长为4厘米,六个圆形的圆心分别在六边形的顶点上。如果小圆的半径为1厘米,求浅灰色部分与涂色部分面积之比。
13.(2024六下·黄石期末) 一辆货车车厢是一个长方体,它的长是6米,宽是1.5米,高是3米。装一车沙子,卸下后沙子堆成一个高是2米的圆锥体,这个沙堆的底面积是多少平方米
14.(2024·绵阳)如图,在一个圆形时钟的表面上,OA表示时针,OB表示分针(O为两针的旋转中心),下午3点时,OA与OB成直角。
(1)分针每分针为 度,时针每分钟转 度;
(2)3:15时,时针与分针所成的角度是 。
(3)在下午3点至4点之间,从下午3点开始,经过 分钟,时针与分针成60°角。
15.(2024六下·瑞安期末)请你结合以下3幅统计图中的信息解决问题。
(1)明明家4月份总支出是 元。
(2)请把条形统计图中“食品”类的直条补充完整。
(3)国际上通常用食品支出占家庭总支出的百分比(即恩格尔系数)来衡量一个国家的人民生活水平。参照下表的恩格尔系数,你觉得明明家处于 生活水平。
恩格尔系数 大于 60% 50%~60% 40%~50% 30%~40% 20%~36% 20%以下
生活水平 贫穷 温饱 小康 相对富裕 富裕 极其富裕
(4)人们都说“近 20年,温州城镇和农村居民的生活水平越来越好。”请结合图表进行数据说明,分析理由。
16.(2024·绵阳)超市推出如下优惠:
⑴一次性购物不超过100元,不享受优惠;
⑵一次性购物超过100元,但不超过300元一律9折;
⑶一次性购物超过300元,一律8折;
两次购物分别付款80元,252元。若一次性购买则应付款多少元?
17.(2024六下·长沙期末)为庆祝“六一”儿童节,学校举办了一场趣味运动会。后勤处共采购了8大箱奖励物资,每箱原价400元。因正遇商家店庆。所有商品一律九折。后勤处购买这批物资实际花了多少钱
18.(2024六下·双流期末)某市大力发展新能源,建造了各种新能源发电厂
某市新能源发电厂投入资金与发电量统计表
类型 风力发电 太阳能发电 水力发电
投入/亿元 8
发电量/亿度 0.8 0.7 1.5
(1)分别求出“风力发电”和“太阳能发电”的投入资金,填入上面表中。
(2)已知这三类新能源发电盘占该地区总发电量的25%,求该地区的总发电量。
19.(2024六下·双流期末)“丝绸之路”是古代连接中西方的商道。传统的丝绸之路起自我国古代都城长安,直延伸到欧洲,在一幅比例尺为1:8000000的地图上约长85厘米,传统的丝绸之路实际全长约为多少千米?
20.(2024六下·双流期末)一台压路机的前轮是圆柱形,轮宽3米,直径1米。压路机前轮转动5周,压路的面积是多少平方米?
21.(2024·钱塘期末)钱塘小学开展阳光体育运动,调查了六年级男生最喜欢的球类运动项目,并将调查情况制成如下统计表和统计图。
(1)将统计表和统计图中的数据补充完整。
项目 排球 篮球 足球 其他
人数 30 30
(2)已知其他球类项目中,有60%的男生最喜欢乒乓球,最喜欢网球的人数与最喜欢乒乓球的人数的比是1∶3,最喜欢网球的有多少人?
22.(2024五下·寻乌期末)黄师傅要做一个长15厘米,宽10厘米,高200厘米的长方体烟囱,至少需要多少平方厘米的铁皮?
23.(2024五下·寻乌期末)在一个长为80厘米,宽为40厘米的玻璃缸中,放入一石块,石块浸没水中,这时水深为30厘米,取出石块后水深为25厘米,这块石块的体积是多少立方分米?
24.(2024六下·黄石期末)张爷爷将50000元存入银行,定期二年,年利率为2.5%。到期后,张爷爷将所得利息捐给了希望工程,他捐出了多少钱
25.(2024五下·寻乌期末)王阿姨今天给月季和君子兰同时浇水,月季每4天浇一次水,君子兰每6天浇一次水,至少多少天后给这两种花同时浇水?
26.(2024六下·重庆市期末)下面是三个图形的旋转。
(1)图②中长方形绕一条边旋转一周,得到图形的体积,是图①中直角三角形绕直角边旋转一周,得到图形体积的 倍。并请说明理由 。
(2)图③中平行四边形绕AB 边旋转一周,得到图形的体积是多少cm3?
27.(2024六下·临平期末)太空育种是当今世界农业领域的尖端科学技术,世界上仅有三个国家拥有该技术,我国就是其中之一。为选取优质小麦种子进行太空培育,某种子基地用A、B、C三种型号的种子进行发芽实验,实验种子数量及发芽情况如下图。
(1)参加发芽实验的三种型号小麦种子共2000粒,其中B型号种子的发芽率是95%,B型号种子的发芽数是 粒。
(2)请将扇形统计图和条形统计图补充完整。
(3)根据实验数据,你建议选取哪种型号的种子进行太空培育比较合适?请说明理由。
28.(2024六下·临平期末)下图中的容器由1个大圆柱和1个小圆柱组成,如果向这个容器匀速注满油,注油过程中,容器中油的高度与所用时间的关系如下图所示。
(1)把下面的大圆柱注满需要 分钟。
(2)上面小圆柱高 厘米。
(3)如果下面大圆柱的底面积是48平方厘米,那么上面小圆柱的底面积是多少?
29.(2024六下·临平期末)只列算式,不计算。
(1)沈叔叔将50000元钱存入银行,整存整取2年。如果年利率是2.2%,到期可取回本金与利息一共多少元?
算式:
(2)一辆变速自行车前齿轮有2个(齿数为48和36),后齿轮有3个(数为20、16和12),这辆自行车的车轮直径是0.7米,蹬一圈,最远能蹬出的距离是多少米?
算式:
30.(2024六下·泗洪期末)李师傅向右图所示的空容器(由上、下两个圆柱组成)中均匀注油,正好注满。注油过程中,容器中油的高度与所用时间的关系如图所示。
(1)把下面的大圆柱注满需 分钟。
(2)上面小圆柱高 厘米。
(3)如果下面的大圆柱的底面积是48平方厘米,那么大圆柱的体积是多少立方厘米?上面小圆柱的底面积是多少平方厘米?(写出计算过程)
31.(2024六下·渝中期末)一个密闭玻璃容器是由一个圆柱和一个圆锥组成的,里面装有一些水(如图1,单位:dm,玻璃厚度忽略不计)。
(1)容器的占地面积是多少平方分米?
(2)容器中水的体积是多少立方分米?
(3)如果将这个容器倒过来(如图2),从水面到圆锥顶点的高度是多少分米?
(2024六下·渝中期末)只列综合算式或方程,不计算。
32.小明爸爸得到一笔 3000 元的劳务报酬,其中 800元是免税,其余部分要按20%的税率缴税。这笔劳务报酬一共要缴税多少元?
33.今年“五·一”期间,解放碑商圈日均迎客约 90万人次,日均客流量比去年同期增长,去年日均客流量为多少万人次?
34.实验小学开展“以纸换树、保护环境”的活动,共回收1.8t 废纸。据统计,每回收 5t废纸进行再利用,相当于保护了 85棵树。实验小学回收的废纸进行再利用,相当于保护了多少棵树?
35.一个零件由两个圆柱组成(如图),它们的高都是10cm,底面半径分别是4cm和8cm。现在要给这个零件的表面涂上颜色,涂色部分共多少 cm2?
36.(2023六下·石城期末)如图所示,有一块长方形铁皮,把其中的阴影部分剪下制成一个圆柱形油桶。(接口处忽略不计)
(1)圆柱形油桶的表面积是多少平方分米?
(2)圆柱形油桶的体积是多少立方分米?
37.(2024六下·越秀期末) 一项工程,若每天工作8小时,则15天可以完成任务。要想12天完成任务,平均每天要工作多少小时 (用比例知识列方程解答)
38.(2024六下·麻城期末)农场在地面上挖了一个圆柱形蓄水池,它的底面周长是125.6米,深是20分米,把底面和侧面抹上水泥,需要抹水泥的面积有多少平方米?这个水池能蓄水多少立方米?
答案解析部分
1.(1)解:10×6+10×7×2+6×7×2
=60+140+84
=284(平方分米)
答:做这个鱼缸至少需要玻璃284平方分米。
(2)解:330升=330立方分米
330÷(10×6)
=330÷60
=5.5(分米)
7﹣5.5=1.5(分米)
答:水面离缸口1.5分米。
(1)长方体的长×宽+长×高×2+宽×高×2=无盖的长方体的表面积;
(2)水的体积÷长方体的底面积=水的高度,长方体的高-水的高度=水面离缸口的高度。
2.解:3.14×(6÷2)2×0.5×3÷2
=3.14×9×0.5×3÷2
=42.39÷2
=21.195(平方厘米)
答:这个铅锤的底面积是21.195平方厘米。
水面升高部分水的体积就是铅锤的体积,因此用玻璃缸的底面积乘水面上升的高低即可求出铅锤的体积。根据圆锥的体积公式,用铅锤的体积乘3再除以高即可求出底面积。
3.解:从图中可以看出,圆锥的高是6厘米,底面半径是2厘米,
圆锥的体积:3.14×2×2×6÷3
=12.56×6÷3
=25.12(立方厘米)
圆柱的底面半径:10÷2=5(厘米)
25.12×3÷(3.14×5×5)
=75.36÷78.5
=0.96(厘米)
答:水面将会下降0.96厘米。
π×底面半径的平方×高÷3=圆锥的体积;圆锥的体积×3÷圆柱的底面积=水面将会下降的高度。
4.(1)
(2)11;12
(3)小红11岁以前不到标准身,可能是缺乏锻炼,挑吃造成的。
(1)根据统计表 的数据描点、连线。
(2)7至8岁增长8厘米,8至9岁增长9厘米,9至10岁增长10厘米,10至11岁增长厘米,11至12岁增长12厘米,所以11岁到12岁增长最快、
(2)主观题,根据图表回答。
5.解:140×3÷
=420÷
=980(千米)
980千米=98000000厘米
98000000×=14(厘米)
答:甲、乙两地之间铁路线的长为14厘米。
用速度乘3求出3小时行驶的路程,根据分数除法的意义,用3小时行驶的路程除以求出全程。把全程换算成厘米,然后用实际距离乘比例尺即可求出图上距离。
6.(1)解:淘气:(25+50+36)÷3=111÷3=37(个)
笑笑:(45+48+30)÷3=123÷3=41(个)
妙想:(40+41+45)÷3=126÷3=42(个)
37<41<42
答:妙想获得第一名。
(2)答:单论最高成绩是50个,所以淘气会获得第一名。
(3)解:按单轮成绩最高排名,淘气获得第一名;
按第一轮成绩排名:25个<40个<45个,笑笑获得第一名;
按第二轮成绩排名:41<48<50,淘气获得第一名;
按第三轮成绩排名:30个<36个<45个,妙想获得第一名;
由此可知:笑笑是本次冠军,是按第一轮的成绩进行排名的。
优点:规则简便容易操作,缺点:不能准确反映三人的真实水平。
(1)先根据“平均数=数据和÷数据个数”,求出三人的平均成绩,再比较大小即可;
(2)分别比较出三轮成绩中9个数字的大小,看谁的单轮成绩最高即可;
(3)先确定是根据平均数还是单轮成绩确定了笑笑是本次冠军,然后分析这个规则的优缺点即可。
7.(1)解:3.14×(12÷2)2×12
=3.14×432
=1356.48(立方厘米)
12×12×12=1728(立方厘米)
1728-1356.48=371.52(立方厘米)
答:这个圆柱的体积是1356.48立方厘米,被切割掉的边角料的体积是371.52立方厘米。
(2)解:3.14×(12÷2÷2)2×12
=3.14×108
=339.12(立方厘米)
1728-339.12×4
=1728-1356.48
=371.52(立方厘米)
答:每个小圆柱的体积是339.12立方厘米,被切割掉的边角料的体积是371.52立方厘米。
(3)解:1728-3.14×(12÷3÷2)2×12×9
=1728-3.14×432
=1728-1356.48
=371.52(立方厘米)
答:被切割的边角料的体积是371.52立方厘米。
(4)答:当被切割出来的圆柱体的个数是n×n时,每个小圆柱体的半径是(12÷n÷2)厘米,每个小圆柱体的体积是(1356.48÷n2)立方厘米。按照这种想法,此时,被切割掉的边角料体积是371.52立方厘米,我发现,被切割掉的边角料的体积是不变的。
(1)这个最大的圆柱的底面直径和高都与正方体的棱长相等,确定圆柱的底面直径和高,用底面积乘高求出圆柱的体积。用正方体的体积减去圆柱的体积求出被切割掉的边角料的体积;
(2)切割出4个大小相等的圆柱,底面半径是(12÷2÷2)厘米,高是12厘米,由此求出一个圆柱的体积。用正方体的体积减去4个这样的圆柱的体积即可求出边角料的体积。
(3)切割出9个大小相等且体积最大的圆柱,底面直径是(12÷3÷2)厘米,高是12厘米,先计算出一个圆柱的体积,然后用正方体的体积减去9个圆柱的体积就是被切割掉的边角料的体积;
(4)用正方体的棱长除以n再除以2求出切割后每个小圆柱的底面半径。切割出的所有圆柱的体积和是不变的,所以用体积和除以n2即可表示出每个小圆柱的体积。每种切割方法下边角料的体积都是不变的。
8.(1)解:10×1.35×365
=13.5×365
=4927.5(元)
答:一年的贷款利息是4927.5元。
(2)解:4927.5÷10000÷1≈4.9%
答:这张借贷卡的贷款年利率是4.9%。
(1)一年的贷款利息=张叔叔借款金额×平均每天的利息×天数;
(2)这张借贷卡的贷款年利率=利息÷本金÷时间。
9.(1)解:350×(1-28%-42%)
=350×30%
=105(人)
答:假性近视的有105人。
(2)解:350×42%=147(人)
350-147=203(人)
(203-147)÷147
=56÷147
≈38.1%
答:六年级视力不良(包括假性近视和近视)的人数比视力正常的人数多总人数的38.1%。
(1)假性近视的人数=星星小学六年级总人数×(1-其余各项分别占的百分率);
(2)六年级视力不良(包括假性近视和近视)的人数比视力正常的人数多总人数的百分率=(六年级视力不良的人数-视力正常的人数)÷视力正常的人数。
10.解:设每天至少应装x台。
(60-20)x=50×60
40x=3000
x=3000÷40
x=75
答:每天至少应装75台。
设每天至少应装x台。依据(计划的天数-提前的天数)×实际平均每天至少装的台数=计划的天数×计划平均每天装的台数,列比例,解比例。
11.(1)解:80×25+2×(80×2+25×2)
=80×25+2×210
=2000+420
=2420(m2)
答:贴瓷砖的面积为2420(m2)。
(2)解:80×25×1.2
=2000×1.2
=2400(m3)
答:需要注入 2400m3的水。
(1)贴瓷砖的面积=长×宽+(长×高+宽×高)×2;
(2)需要注入水的体积=游泳池的长×宽×水面的高度。
12.解:浅灰色部分的面积=一个小圆的面积+一个大圆的面积,
深灰色部分面积=2个小圆的面积+2个大圆的面积=2×(一个小圆的面积+一个大圆的面积)=2×浅灰色部分的面积;
所以浅灰色部分与深灰色部分面积之比是1:2。
正六边形的内角和是720度,相当于两个圆的内角和,所以浅灰色部分的面积=一个小圆的面积+一个大圆的面积;那么外面深灰色部分面积=2个小圆的面积+2个大圆的面积;即外面深灰色部分面积=2×(一个小圆的面积+一个大圆的面积);由此确定浅灰色部分与深灰色部分的面积比即可。
13.解:6×1.5×3×3÷2
=27×3÷2
=81÷2
=40.5(平方米)
答:这个沙堆的底面积是40.5平方米。
这个沙堆的底面积=长方体车厢的长×宽×高×3÷圆锥的高。
14.(1)6;0.5
(2)7.5°
(3)或
解:(1)分针每分钟转:360°÷60=6°,时针每分钟转30°÷60=0.5°;
(2)0.5×15=7.5°;
(3)当分针在时针上方时:
(90-60)÷(6-0.5)
=30÷5.5
=(分钟)
当分针在时针下方时:
(90+60)÷(6-0.5)
=150÷5.5
=(分钟)
故答案为:(1)6;0.5;(2)7.5°;(3)或。
(1)分针走1圈是60分,一圈是360°,所以用360除以60就是分针每分钟转的度数。时针走1大格是60分,一大格是30°,所以用30除以60即可求出时针每分钟走的度数;
(2)3:15,分针指向3,时针超过3,因此只需要计算时针15分钟走的度数就是两针之间夹角的度数;
(3)要分两种情况考虑,根据追及问题解答。第一种情况:分针在时针的上面,也就是分针没有追上时针。原来两针之间夹角是90°,现在是60°,说明分针追时针了(90-60),用追及度数除以每分钟追的度数即可求出经过的时间。第二种情况,分针超过时针,也就是先追上90°,再超过时针60°,这样分针追了(90+60),用追的度数除以每分钟追的度数即可求出经过的时间。
15.(1)12000
(2)解:12000×(1-30%-10%-35%)
=12000×0.25
=3000(元)
(3)富裕
(4)解:从第三个图可以看出,近20年,恩格尔系数越来越小,说明温州城镇和农村居民的生活水平越来越好。
解:(1)1200÷10%=12000(元)
明明家4月份总支出是12000元。
(3)1-30%-10%-35%=25%
25%在20%~36%之间,属于富裕。
故答案为:(1)12000;(3)富裕。
(1)服装的支出÷服装的支出占总支出的百分率=总支出;
(2)总支出×食品的支出占总支出的百分率=食品的支出,据此作图;
(3)单位1-教育服装其它分别占的百分比=食品占的百分比,据此解答;
(4)答案不唯一,合理即可。
16.解:一次性购物超过100元,但不超过300元一律9折则在这个范围内最低付款90元,因而第一次付款80元,没有优惠;
第二次购物时:是第二种优惠,可得出原价是 252÷90%=280(符合超过100不高于300);
则两次共付款:80+280=360元,超过300元,则一次性购买应付款:360×080%=288元;
当第二次付款是超过300元时:可得出原价是 252÷080%=315(符合超过300元),
则两次共应付款:80+315=395元,则一次性购买应付款:395×80%=316元。
答:则一次性购买应付款288元或316元。
第一次购物的80元是没有优惠的。第二次购物的252元分两种情况,也就是可能享受的九折优惠,也可能销售的八折优惠。由此分两种情况计算出第二次购物的原价,进而分两种情况计算一次性购物应付的钱数即可。
17.解:400×90%×8
=360×8
=2880(元)
答:后勤处购买这批物资实际花了2880元。
每箱原价×折扣=每箱的现价,每箱的现价×买的箱数=一共花的钱数。
18.(1)解:8÷50%=16(亿元),
太阳能发电:16×20%=3.2(亿元),
风力发电:16×30%=4.8(亿元),
如下表所示:
类型 风力发电 太阳能发电 水力发电
投入/亿元 4.8 3.2 8
发电量/亿度 0.8 0.7 1.5
(2)解:(0.8+0.7+1.5)÷25%
=3÷25%
=12(亿度)
答:该地区的总发电量12亿度。
(1)根据资金与发电量统计表可知水力发电投入资金为8亿元,根据扇形统计图可知水力发电投入资金占该市新能源发电投入资金的50%,根据已知一个数的百分之几是多少,求这个数,用除法计算,用水力发电投入的资金除以水力发电投入资金占该市新能源发电投入资金的百分数即可求出该市投入新能源发电厂的资金;根据求一个数的已分之几是多少,用乘法计算,用该市投入新能源发电的资金乘太阳能发电和风力发电占该市投入新能源发电资金的百分数即可求出太阳能发电和风力发电投入的资金;
(2)根据(1)可知三种新能源发电的度数,根据加法意义,把风力发电、太阳能发电、水力发电的度数之和相加求和即可求出该市新能源发电的度数之和,根据已知一个数的百分之几是多少,求这个数,用除法计算,用新能源发电的度数之和除以三类新能源发电量占该地区总发电量的百分数即可求出该地区的总发电量。
19.解:88÷= 704000000(厘米),
704000000厘米=7040千米;
答:传统的丝绸之路实际全长约为7040千米。
根据比例尺=图上距离÷实际距离,实际距离=图上距离÷比例尺,据此求解。
20.解:轮宽看做圆柱的高,
3.14×1×3×5
=9.42×5
=47.1(平方米)
答:压路的面积是47.1平方米。
压路机的前轮转动一圈压路的面积就是圆柱的侧面积,π×直径=底面周长,底面周长×高=侧面积,侧面积×5=转动5周压路的面积。
21.(1)解:1-25%-25%-12.5=37.5%
30÷25%=120(人)
120×37.5%=45(人)
120×12.5%=15(人)
项目 排球 篮球 足球 其他
人数 30 30 45 15
(2)解:15×60%=9(人)
9÷3=3(人)
答:最喜欢网球的有3人。
(1)排球占25%,足球占的分率=1-其余各项分别占的百分率;
喜欢足球的人数=总人数×喜欢足球占的分率;其中,总人数=喜欢篮球的人数÷喜欢篮球占的分率;
喜欢其他的人数=总人数×喜欢其他占的分率,然后填写统计表和统计图;
(2)最喜欢网球的人数=最喜欢乒乓球的人数÷3,其中,最喜欢乒乓球的人数=喜欢其他的人数×60%。
22.解:(10×200+15×200)×2
=5000×2
=10000(平方厘米)
答:至少需要10000平方厘米的铁皮。
制做长方体烟囱,至少需要多少平方厘米的铁皮,只需要求前后左右4个面的面积。
23.解:80×40×(30-25)
=3200×5
=16000(平方厘米)
=16(立方分米)
答:这块石块的体积是16立方分米。
排水法求不规则物体的体积,石块浸没在水中,水上升(下降)的体积就是不规则物体的体积。
24.解:50000×2×2.5%
=100000×2.5%
=2500(元)
答:他捐了2500元。
张爷爷捐的钱数=所得利息,其中,利息=本金×利率×存期。
25.解:月季每4天浇一次水,浇水时间是第4、8、12、16、20、24……
君子兰每6天浇一次水,浇水时间是第6、12、18、24……
共同浇水时间是12、24……
答:至少12天后给这两种花同时浇水。
根据题意,月季每4天浇一次水,君子兰每6天浇一次水,那么每4和6的最小公倍数天后两种花同时浇水,据此解答。
26.(1)3;因为等底等高的圆柱的体积是圆锥体积的3倍
(2)解:3.14×4×4×3
=50.24×3
=150.72(立方厘米)
答:得到图形的体积是150.72立方厘米。
解:(1)图②中长方形绕一条边旋转一周,得到图形的体积,是图①中直角三角形绕直角边旋转一周,得到图形体积的3倍,因为等底等高的圆柱的体积是圆锥体积的3倍。
故答案为:(1)3;因为等底等高的圆柱的体积是圆锥体积的3倍。
图③中平行四边形绕AB 边旋转一周,得到图形的体积=圆柱的体积=π×半径×半径×高。
27.(1)665
(2)解:1-35%-35%=30%
(3)解:644÷(2000×35%)
=644÷700
=92%
518÷(2000×30%)
=518÷600
≈86.33
95%>93%>86.33%
答:建议选取B种型号的种子进行太空培育比较合适,因为这种的发芽率高。
解:(1)2000×35%×95%
=700×95%
=665(粒)。
故答案为:(1)665。
(1)B型号种子的发芽数=参加发芽实验的三种型号小麦种总粒数×B占的分率×B型号种子的发芽率;
(2)C占的百分率=1-其余各项分别占的百分率;画出直条,并且标上数据;
(3)发芽率=A、C分别发芽的种子粒数÷(参加发芽实验总粒数×各自分别占的百分率),然后比较大小,要选择发芽率高的种子。
28.(1)8
(2)30
(3)解:48×20÷8
=960÷8
=120(立方厘米)
120×(12-8)÷30
=480÷30
=16(平方厘米)
答:上面小圆柱的底面积是16平方厘米。
解:(1)把下面的大圆柱注满需要8分钟;
(2)50-20=30(厘米),上面小圆柱高30厘米。
故答案为:(1)8;(2)30。
(1)观察统计图可知:把下面的大圆柱注满需要8分钟;
(2)上面小圆柱的高=总高度-大圆柱的高;
(3)平均每分钟注水的体积=大圆柱的体积÷大圆柱注满水需要的时间,其中,大圆柱的体积=底面积×大圆柱的高,上面小圆柱的底面积= 平均每分钟注水的体积×(12-8)÷小圆柱的高。
29.(1)解:50000×2×2.2%+50000
(2)解:3.14×0.7×(48÷12)
(1)到期可取回本金与利息总钱数=本金+利息,其中,利息=本金×利率×存期;
(2)最远能蹬出的距离=π×直径×蹬一圈自行车走的圈数;其中,蹬一圈自行车走的圈数=48÷12。
30.(1)1
(2)30
(3)解:48×20=960(立方厘米)
960÷1=720(立方厘米)
720×=480(立方厘米)
480÷30=16(平方厘米)
答:上面小圆柱的底面积是16平方厘米。
解:(1)1+1÷3=1+=1(分)
把下面的大圆柱注满需1分钟。
(2)50-20=30(厘米)
上面小圆柱高30厘米。
故答案为:(1)1;(2)30。
(1)1分钟背平均分成3份,1份是分钟,据此解答;
(2)20~50之间的长度就是小圆柱的高;
(3)大圆柱的底面积×大圆柱的高=大圆柱的体积,大圆柱的体积÷用的时间=1分钟注入油的体积,1分钟注入油的体积×小圆柱注入的时间=小圆柱的体积,小圆柱的体积÷小圆柱的高=小圆柱的底面积。
31.(1)解:3.14×(9÷2)2
=3.14×4.52
=3.14×20.25
=63.585(平方分米)
答: 容器的占地面积是63.585平方分米。
(2)解:63.585×6=381.51(立方分米 )
答: 容器中水的体积是381.51 立方分米 。
(3)解:(381.51-63.585×6×)÷63.585
=(381.51-381.51×)÷63.585
=(381.51-127.7)÷63.585
=254.34÷63.585
=4(分米)
4+6=10(分米)
答: 从水面到圆锥顶点的高度是10分米。
(1)求容器占地面积,就是求这个容器的底面积,根据圆的面积公式:,代入数据,即可解答。
(2)容器中的水的体积,就是底面直径是9分米,高是6分米的圆柱的体积,根据圆柱的体积公式:V=底面积×高,代入数据,即可解答。
(3)根据圆锥的体积公式:V=底面积×高×,代入数据,求出圆锥部分水的体积;由于水的体积不变,再用原来水的体积一圆锥部分的体积,求出网柱部分水的体积,再根据高=圆柱的体积÷圆柱的底面积,代入数据,求出圆柱部分水的高度,再加上圆锥部分的高度,即可解答。
32.解:(3000-800)×20%
33.解:90÷(1+)
34.解:85÷5×1.8
35.解:2×3.14×4×10+2×3.14×8×10+3.14×82×2
(1)考查的是税率的应用;(2)考查的是分数除法的应用;(3)考查的是正比例的应用;(4)考查的是关于圆柱体的组合体表面积的计算,注意重合部分不涂色。
32.应纳税部分×税率=应纳税额,求他缴纳的税,就是求一个数的百分之几是多少,用乘法计算即可,据此解答。
33.比去年同期增长就是(1+),本题中单位“1”的量“去年同日均客流量”未知,所以用除法计算,据此解答。
34.根据题意知道,每回收5t废纸进行再利用,相当于保护了85棵树。因此,1t废纸进行再利用能保护的树的数量为(85÷5)棵,实验小学回收了1.8t废纸,那么,实验小学回收的废纸进行再利用,相当于保护的树的数量为(85÷5×1.8) 棵。
35.由于大小两个圆柱粘合在一起,所以上面的小圆柱只求侧面积,下面的大圆柱求出表面积,然后合并起来就是需要涂色的面积,根据圆柱的表面积=侧面积+底面积×2;据此把数据代入公式解答。
36.(1)18.84÷3.14=6(分米)
10-6=4(分米)
18.84×4+3.14×(6÷2)2×2
=75.36+3.14×9×2
=75.36+56.52
=131.88(平方分米)
答:圆柱形油桶的表面积是131.88平方分米。
(2)3.14×(6÷2)2×4
=3.14×9×4
=28.26×4
=113.04(立方分米)
答:圆柱形油桶的体积是113.04立方分米。
(1)根据圆柱的表面积=侧面积+底面积×2,首先根据圆的周长公式:C=πd,那么d=C÷π,据此求出圆柱的底面直径,圆柱的高用长方形铁皮的宽减去圆柱的底面直径,然后把数据代入公式解答。
(2)根据圆柱的体积公式:V=,把数据代入公式解答。
37.解:平均每天要工作x小时。
8×15=12x
12x=120
x=120÷12
x=10
答:平均每天要工作10小时。
设平均每天要工作x小时。依据计划工作的时间×计划的天数=实际工作的时间×实际工作的天数,列比例,解比例。
38.解:20分米=2米
125.6÷3.14÷2
=40÷2
=20(米)
125.6×2+3.14×202
=251.2+3.14×400
=251.2+1256
=1507.2(平方米)
3.14×202×2
=3.14×400×2
=1256×2
=2512(立方米)
答:需要抹水泥的面积有1507.2平方米;这个水池能蓄水2512立方米。
抹水泥的面积等于圆柱的侧面积加圆柱的底面积,圆柱的侧面积=底面周长×高,圆柱的底面积=π×半径2;圆柱的容积=π×半径2×高,据此代入数值计算即可。
同课章节目录
