湖南省长沙市明德中学2024-2025学年高一下学期5月阶段检测数学试题(含答案)
文档属性
| 名称 | 湖南省长沙市明德中学2024-2025学年高一下学期5月阶段检测数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 779.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 09:25:01 | ||
图片预览




文档简介
湖南省长沙市明德中学2024-2025学年高一下学期5月阶段检测数学试题
时量:120分钟 满分:150分
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项符合题目要求.
1.已知集合,则( )
A. B. C. D.
2.已知,则在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知a,b是空间中的两条直线,则“”是“a,b无公共点”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
4.一支游泳队有男运动员28人,女运动员20人,按照性别进行分层,样本按比例分配,用分层随机抽样的方法从该游泳队中抽取了男运动员7人,则女运动员被抽取的人数为( )
A.4 B.5 C.6 D.7
5.函数的图象如图所示,则( )
A.1 B. C.2 D.
6.已知,则( )
A. B. C. D.
7.在流行病学中,基本传染数是指每名感染者平均可传染的人数.假设某种传染病的基本传染数为个感染者在每个传染期会接触到个新人,这个人中有个人接种过疫苗(称为接种率),那么1个感染者传染人数为.已知某种传染病在某地的基本传染数,为了使1个感染者传染人数不超过1,则该地疫苗的接种率至少为( )
A. B. C. D.
8.如图,已知,任意点关于点的对称点为,点关于点的对称点为,则( )
A.1 B. C.2 D.
二、多项选择题:本题共3小题,每小题6分,共18分,在每小题给出的四个选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.设样本空间含有等可能样本点,且,则下列说法正确的是( )
A.事件与为互斥事件 B.事件与为对立事件
C.事件两两相互独立 D.
10.已知正方体的棱长为1,下列说法正确的是( )
A. B.与所成的角为
C.与平面所成的角为 D.到平面的距离为
11.在人工神经网络中,单个神经元输入与输出的函数关系可以称为激励函数.双曲正切函数是一种激励函数.定义双曲正弦函数,双曲余弦函数,双曲正切函数.则下列说法正确的有( )
A. B.
C.是奇函数 D.对任意的,存在唯一的,使.
三、填空题:本题共3小题,每小题5分,共15分.
12.函数的最小正周期是___________.
13.数据的平均数,方差,若,则数据的平均数___________,方差___________.
14.某封闭的圆锥容器的轴截面为等边三角形,高为6.一个半径为1的小球在该容器内自由运动,则小球能接触到的圆锥容器内壁的最大面积为___________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)如图,在直三棱柱中,为的中点,为棱的中点.求证:
(1)平面ABC;
(2)平面平面.
16.(15分)为了解中学生的体育锻炼情况,调查小组在某中学随机抽取了100名学生,统计了他们某一周的综合体育活动时间(单位:时),并按照将样本数据分成6组,制成如图所示的频率分布直方图.
(1)补全频率分布直方图,并估计该校学生每周综合体育活动时间的中位数与平均数;
(2)利用频率估计概率,若从该校随机抽取两名学生,且两名学生的体育活动情况互不影响,求这两名学生中至少有一人每周综合体育活动时间不低于8小时的概率.
17.(15分)已知的内角的对边分别为,已知向量,且.
(1)求;
(2)若的面积为,且,求的周长.
18.(17分)已知,设是函数的图象上任意两点,点满足,其中为坐标原点.
(1)求的零点;
(2)若,求值;
(3)若,求的最小值.
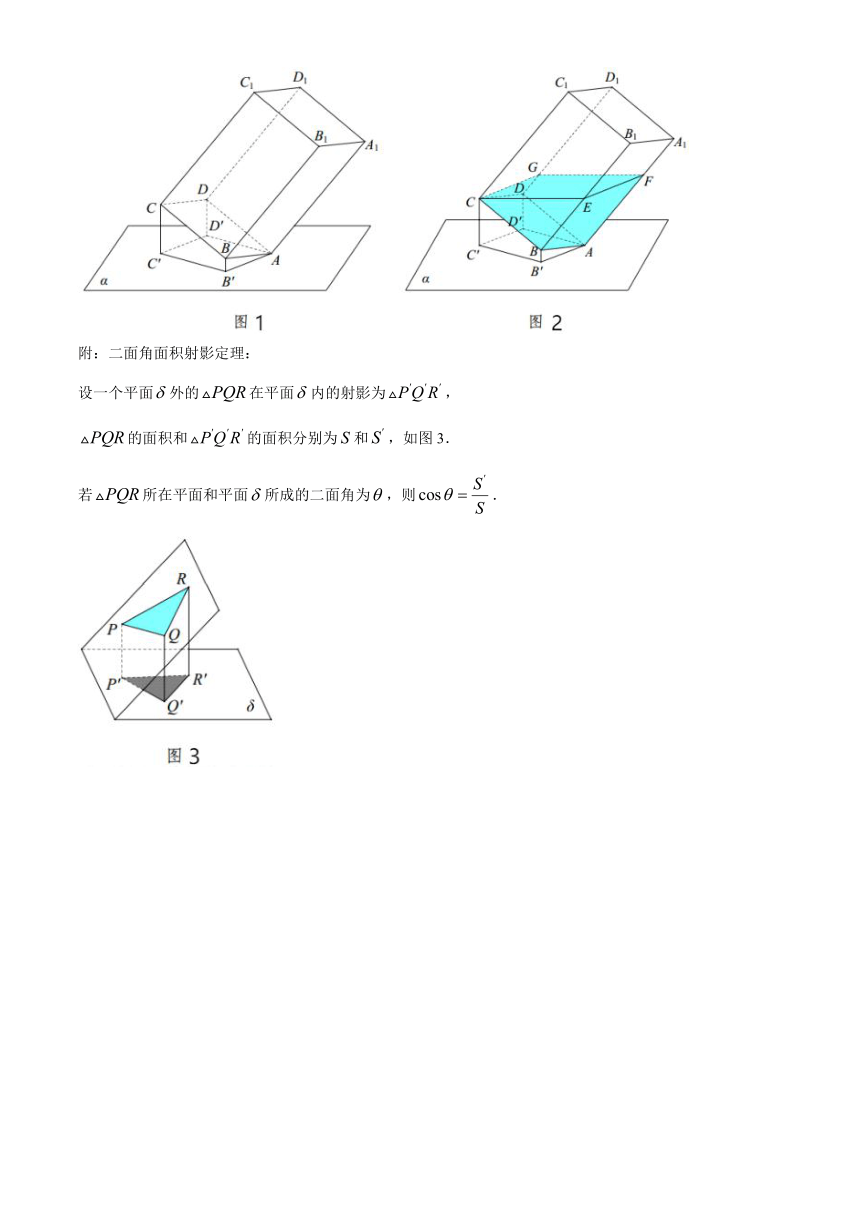
19.(17分)如图1,一个透明塑料制成的长方体容器,若固定容器底面一个顶点于平面上,再将容器倾斜,使得顶点到平面的距离分别为,且在平面内的射影分别为.
(1)求证:,且四边形为平行四边形;
(2)若,
①求平面ABCD与平面所成二面角的余弦值;
②若往容器灌进一些水,使水面刚好过顶点,水面所在四边形为CEFG,求灌进水的体积.
附:二面角面积射影定理:
设一个平面外的在平面内的射影为,
的面积和的面积分别为和,如图3.
若所在平面和平面所成的二面角为,则.
明德中学2025年上学期高一年级5月阶段检测
数学试题答案
题号 1 2 3 4 5 6 7 8
答案 D B A B C B D C
题号 9 10 11 12 13 14
答案 BC ABD ACD 25;80
15.证明(1)取AB的中点,连接PD,CD.
因为P,D分别是的中点,且,
又三棱柱中,,而为棱的中点,所以,且,
所以,所以四边形PDCQ为平行四边形,因此.
又平面平面ABC,所以平面ABC.…………………………………………6分
(2)直三棱柱中,平面ABC,又平面ABC,所以,
又为AB的中点,所以.
又,所以平面.
由(1)知,,所以平面.
又平面,所以平面平面.………………………………………………13分
16.解(1)第五组的频率为,
所以该组对应的小矩形高度为,故补全频率分布直方图如下:
………………………………………………3分
设样本数据的中位数为,平均数为
因为样本数据在的频率为,
因为样本数据在的频率为,
则,所以,解得,…………………………………6分
故估计样本中位数为6.4.
故估计样本平均数为6.2.
由样本估计总体,该校学生每周综合体育活动时间的中位数与平均数分别为6.4和6.2.
(说明:此处没有用样本估计总体,只估计样本中位数和平均数,扣1分)
(2)由频率分布直方图可估计该校学生每周综合体育活动时间不低于8小时的频率为.
记事件“抽取的第1名学生每周综合体育活动时间不低于8小时”,“抽取的第2名学生每周综合体育活动时间不低于8小时”,由题意相互独立.
利用频率估计概率,.………………………………………………12分
记事件“抽取的两名学生中至少有一人每周综合体育活动时间不低于8小时”,则
所以抽取的两名学生中至少有一人每周综合体育活动时间不低于8小时的概率为0.51.……………15分
(说明:没有必要文字说明、表述不规范、未作答等情况,酌情扣分)
17.解(1)由知,,………………………………………………………2分
由正弦定理得,,…………………………………………………………4分
因为,所以.
则,即,又,所以.……………………………………7分
(说明:没有说明,扣1分)
(2)法一:因为的面积为,得,
又,因此.…………………………………………………………9分
又,所以.从而………………………………………11分
所以.
又由得,,因此.
由余弦定理得,,所以.
所以的周长为.……………………………………………………15分
法二:因为的面积为,得.
又.……………………………………………………………………………9分
所以,又,所以.
又,所以.从而………………………………………11分
设的外接圆半径为,由正弦定理,得
所以,的面积.
又,所以.………………………………………………………………………13分
所以的周长为.……………………15分
18.解(1)令得,解得.
所以的零点为.……………………………………………………………………………3分
(2)由,可得,即,则…………………………………………9分
(3)由得,所以的定义域为.
由,得.…………………………………………………………………………11分
…………………………………………14分
当且仅当即时,等号成立.所以的最小值为.……………………17分
19.解(1)由题意,,则.
设在平面的射影为,即,
由线面平行性质定理,得,
又分别为BD,AC的中点,所以既是的中位线,也是梯形的中位线.
所以,即.………………………………………………3分
由是的中位线,得.
由是梯形的中位线,得.
所以,四边形为平行四边形.…………………………………………………………………5分
(2)因为,由(1)知,,即.
①由,得,由,得.
又,得.
所以由余弦定理,得,所以.
设平行四边形的面积为,因此…………………8分
又四边形ABCD的面积.
设平面ABCD与平面所成的角为,则根据二面角的面积射影定理,得.
所以平面ABCD与平面所成的角的余弦值为.………………………………………………10分
②设长方体侧棱与平面所成的角为.
因为平面ABCD,又平面与平面ABCD所成角为,所以.
由①得,.所以.………………………………13分
因为水面所在四边形平面,所以到平面的距离等于到平面的距离4.
由,得.……………………………………………………………15分
过作平面ABCD的平行平面FMNT,交分别于.
由(1)结论,.
所以,几何体与几何体的体积相等.
因此,容器中灌进水的体积为.
所以灌进水的体积为.………………………………………………………………………17分
时量:120分钟 满分:150分
一、单项选择题:本题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项符合题目要求.
1.已知集合,则( )
A. B. C. D.
2.已知,则在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.已知a,b是空间中的两条直线,则“”是“a,b无公共点”的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
4.一支游泳队有男运动员28人,女运动员20人,按照性别进行分层,样本按比例分配,用分层随机抽样的方法从该游泳队中抽取了男运动员7人,则女运动员被抽取的人数为( )
A.4 B.5 C.6 D.7
5.函数的图象如图所示,则( )
A.1 B. C.2 D.
6.已知,则( )
A. B. C. D.
7.在流行病学中,基本传染数是指每名感染者平均可传染的人数.假设某种传染病的基本传染数为个感染者在每个传染期会接触到个新人,这个人中有个人接种过疫苗(称为接种率),那么1个感染者传染人数为.已知某种传染病在某地的基本传染数,为了使1个感染者传染人数不超过1,则该地疫苗的接种率至少为( )
A. B. C. D.
8.如图,已知,任意点关于点的对称点为,点关于点的对称点为,则( )
A.1 B. C.2 D.
二、多项选择题:本题共3小题,每小题6分,共18分,在每小题给出的四个选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.设样本空间含有等可能样本点,且,则下列说法正确的是( )
A.事件与为互斥事件 B.事件与为对立事件
C.事件两两相互独立 D.
10.已知正方体的棱长为1,下列说法正确的是( )
A. B.与所成的角为
C.与平面所成的角为 D.到平面的距离为
11.在人工神经网络中,单个神经元输入与输出的函数关系可以称为激励函数.双曲正切函数是一种激励函数.定义双曲正弦函数,双曲余弦函数,双曲正切函数.则下列说法正确的有( )
A. B.
C.是奇函数 D.对任意的,存在唯一的,使.
三、填空题:本题共3小题,每小题5分,共15分.
12.函数的最小正周期是___________.
13.数据的平均数,方差,若,则数据的平均数___________,方差___________.
14.某封闭的圆锥容器的轴截面为等边三角形,高为6.一个半径为1的小球在该容器内自由运动,则小球能接触到的圆锥容器内壁的最大面积为___________.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)如图,在直三棱柱中,为的中点,为棱的中点.求证:
(1)平面ABC;
(2)平面平面.
16.(15分)为了解中学生的体育锻炼情况,调查小组在某中学随机抽取了100名学生,统计了他们某一周的综合体育活动时间(单位:时),并按照将样本数据分成6组,制成如图所示的频率分布直方图.
(1)补全频率分布直方图,并估计该校学生每周综合体育活动时间的中位数与平均数;
(2)利用频率估计概率,若从该校随机抽取两名学生,且两名学生的体育活动情况互不影响,求这两名学生中至少有一人每周综合体育活动时间不低于8小时的概率.
17.(15分)已知的内角的对边分别为,已知向量,且.
(1)求;
(2)若的面积为,且,求的周长.
18.(17分)已知,设是函数的图象上任意两点,点满足,其中为坐标原点.
(1)求的零点;
(2)若,求值;
(3)若,求的最小值.
19.(17分)如图1,一个透明塑料制成的长方体容器,若固定容器底面一个顶点于平面上,再将容器倾斜,使得顶点到平面的距离分别为,且在平面内的射影分别为.
(1)求证:,且四边形为平行四边形;
(2)若,
①求平面ABCD与平面所成二面角的余弦值;
②若往容器灌进一些水,使水面刚好过顶点,水面所在四边形为CEFG,求灌进水的体积.
附:二面角面积射影定理:
设一个平面外的在平面内的射影为,
的面积和的面积分别为和,如图3.
若所在平面和平面所成的二面角为,则.
明德中学2025年上学期高一年级5月阶段检测
数学试题答案
题号 1 2 3 4 5 6 7 8
答案 D B A B C B D C
题号 9 10 11 12 13 14
答案 BC ABD ACD 25;80
15.证明(1)取AB的中点,连接PD,CD.
因为P,D分别是的中点,且,
又三棱柱中,,而为棱的中点,所以,且,
所以,所以四边形PDCQ为平行四边形,因此.
又平面平面ABC,所以平面ABC.…………………………………………6分
(2)直三棱柱中,平面ABC,又平面ABC,所以,
又为AB的中点,所以.
又,所以平面.
由(1)知,,所以平面.
又平面,所以平面平面.………………………………………………13分
16.解(1)第五组的频率为,
所以该组对应的小矩形高度为,故补全频率分布直方图如下:
………………………………………………3分
设样本数据的中位数为,平均数为
因为样本数据在的频率为,
因为样本数据在的频率为,
则,所以,解得,…………………………………6分
故估计样本中位数为6.4.
故估计样本平均数为6.2.
由样本估计总体,该校学生每周综合体育活动时间的中位数与平均数分别为6.4和6.2.
(说明:此处没有用样本估计总体,只估计样本中位数和平均数,扣1分)
(2)由频率分布直方图可估计该校学生每周综合体育活动时间不低于8小时的频率为.
记事件“抽取的第1名学生每周综合体育活动时间不低于8小时”,“抽取的第2名学生每周综合体育活动时间不低于8小时”,由题意相互独立.
利用频率估计概率,.………………………………………………12分
记事件“抽取的两名学生中至少有一人每周综合体育活动时间不低于8小时”,则
所以抽取的两名学生中至少有一人每周综合体育活动时间不低于8小时的概率为0.51.……………15分
(说明:没有必要文字说明、表述不规范、未作答等情况,酌情扣分)
17.解(1)由知,,………………………………………………………2分
由正弦定理得,,…………………………………………………………4分
因为,所以.
则,即,又,所以.……………………………………7分
(说明:没有说明,扣1分)
(2)法一:因为的面积为,得,
又,因此.…………………………………………………………9分
又,所以.从而………………………………………11分
所以.
又由得,,因此.
由余弦定理得,,所以.
所以的周长为.……………………………………………………15分
法二:因为的面积为,得.
又.……………………………………………………………………………9分
所以,又,所以.
又,所以.从而………………………………………11分
设的外接圆半径为,由正弦定理,得
所以,的面积.
又,所以.………………………………………………………………………13分
所以的周长为.……………………15分
18.解(1)令得,解得.
所以的零点为.……………………………………………………………………………3分
(2)由,可得,即,则…………………………………………9分
(3)由得,所以的定义域为.
由,得.…………………………………………………………………………11分
…………………………………………14分
当且仅当即时,等号成立.所以的最小值为.……………………17分
19.解(1)由题意,,则.
设在平面的射影为,即,
由线面平行性质定理,得,
又分别为BD,AC的中点,所以既是的中位线,也是梯形的中位线.
所以,即.………………………………………………3分
由是的中位线,得.
由是梯形的中位线,得.
所以,四边形为平行四边形.…………………………………………………………………5分
(2)因为,由(1)知,,即.
①由,得,由,得.
又,得.
所以由余弦定理,得,所以.
设平行四边形的面积为,因此…………………8分
又四边形ABCD的面积.
设平面ABCD与平面所成的角为,则根据二面角的面积射影定理,得.
所以平面ABCD与平面所成的角的余弦值为.………………………………………………10分
②设长方体侧棱与平面所成的角为.
因为平面ABCD,又平面与平面ABCD所成角为,所以.
由①得,.所以.………………………………13分
因为水面所在四边形平面,所以到平面的距离等于到平面的距离4.
由,得.……………………………………………………………15分
过作平面ABCD的平行平面FMNT,交分别于.
由(1)结论,.
所以,几何体与几何体的体积相等.
因此,容器中灌进水的体积为.
所以灌进水的体积为.………………………………………………………………………17分
同课章节目录
