安徽省阜阳市临泉田家炳实验中学(临泉县教师进修学校)2024-2025学年高一下学期5月月考数学试题(含答案)
文档属性
| 名称 | 安徽省阜阳市临泉田家炳实验中学(临泉县教师进修学校)2024-2025学年高一下学期5月月考数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 91.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 09:32:38 | ||
图片预览


文档简介
高一数学5月试卷
(120分钟 150分)
考试范围: 《必修第二册》第六章(20%)+第七章(10%)+第八章(25%)+第九章(45%)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若z-2i=2+i,则|z|=()
A.2 B. C. D.
2.若向量a=(2,1),b=(0,-1),则a在b上的投影向量为()
A.(0,-1) B.(0,1) C.(2,0) D.(0,2)
3.某校高一、高二、高三年级的学生人数之比为3∶3∶4,现用分层随机抽样的方法从该校三个年级的学生中抽取容量为200的样本,则从高一年级抽取的学生人数为()
A.60 B.80 C.100 D.50
4.如图,在正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,则直线AM与BN的关系是()
A.相交
B.平行
C.异面
D.垂直
5.在平行四边形ABCD中,点E是AD的中点,点F是CD的一个三等分点(靠近点C),则=()
A.+ B.+
C.+ D.-
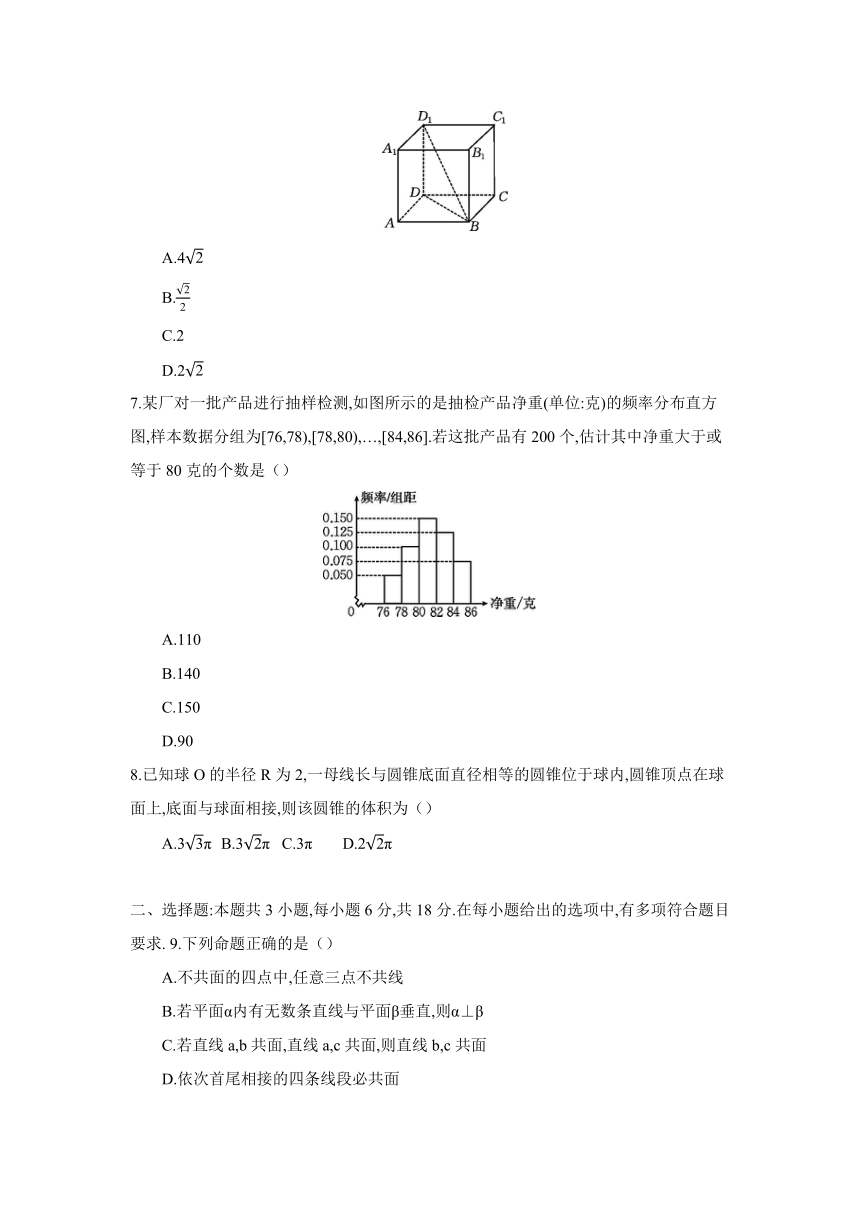
6.如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形且边长为3,BD1与底面所成角的正切值为,则该直四棱柱的侧棱长为()
A.4
B.
C.2
D.2
7.某厂对一批产品进行抽样检测,如图所示的是抽检产品净重(单位:克)的频率分布直方图,样本数据分组为[76,78),[78,80),…,[84,86].若这批产品有200个,估计其中净重大于或等于80克的个数是()
A.110
B.140
C.150
D.90
8.已知球O的半径R为2,一母线长与圆锥底面直径相等的圆锥位于球内,圆锥顶点在球面上,底面与球面相接,则该圆锥的体积为()
A.3π B.3π C.3π D.2π
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求. 9.下列命题正确的是()
A.不共面的四点中,任意三点不共线
B.若平面α内有无数条直线与平面β垂直,则α⊥β
C.若直线a,b共面,直线a,c共面,则直线b,c共面
D.依次首尾相接的四条线段必共面
10.从某项综合能力测试中抽取100人的成绩,统计如下表,则()
分数 5 4 3 2 1
人数 30 30 20 10 10
A.这100人的成绩的平均数为3.4 B.这100人的成绩的平均数为3.6
C.这100人的成绩的方差为1.61 D.这100人的成绩的方差为1.64
11.下列说法不正确的有()
A.若z∈C,则z2≥0
B.若a>b,则a+i>b+i
C.若z1,z2∈C,且+=0,则z1=z2=0
D.若复数z满足|z|=1,则|z+2i|的最大值为3
三、填空题:本题共3小题,每小题5分,共15分.
12.在等腰△ABC中,BC=2,AB=AC,则·= .
13.如图,在三棱锥P-ABC中,PA⊥平面ABC,若AB=AC=1,BC=,则二面角B-PA-C的大小为 .
14.若f(n)=()n+((n∈N*),则集合{x|x=f(n)}中共有 个元素.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
已知|a|=2,|b|=.
(1)若a,b的夹角为45°,求|a-b|;
(2)若(a+b)⊥b,求a与b的夹角θ.
16.(15分)
已知复数z1=(-b-1)+(1-b)i,z2=,其中a,b∈R.
(1)若z1为纯虚数,求b的值;
(2)若z1与z2互为共轭复数,求a+b的值.
17.(15分)
已知向量m=(2sin A,1),n=(cos A-sin A,-1),m⊥n,其中A是△ABC的内角,· >0.
(1)求角A的大小;
(2)若角A,B,C所对的边分别为a,b,c,且a=1,求b+c的取值范围.
18.(17分)
某学校高中部最近组织了一次野外郊游活动,活动分为登山看日出组和海边看日落组,且每位学生至多参加其中一组.在参加活动的学生中,高一学生占20%,高二学生占30%,登山组的学生占参加活动的总人数的,且该组高一学生占50%,高二学生占30%.为了了解各组不同年级的学生对本次活动的满意程度,现用分层随机抽样的方法从参加活动的全体学生中抽取一个容量为80的样本.
(1)求在海边看日落组中,高一学生、高二学生、高三学生分别所占的比例;
(2)求在海边看日落组中,高三年级应抽取的人数.
19.(17分)
如图,在三棱锥P-ABC中,PA⊥底面ABC,若二面角P-BC-A的大小为30°,BC⊥AB,AC=2,PA=1,M是PB上的一点,且PB=4PM,N是PC上靠近点C的三等分点.
(1)求直线AB与直线PC所成角的余弦值;
(2)求三棱锥P-AMN的体积.
答案与解析
题序 1 2 3 4 5 6 7 8 9 10 11
答案 C B A C A D B C AB BD ABC
12. 【解析】在等腰△ABC中,BC=2,AB=AC,则·=||·||·cos(π-B)=-||2=-2.
【答案】-2
13. 【解析】因为PA⊥平面ABC,所以PA⊥AB,PA⊥AC,所以∠BAC是二面角B-PA-C的平面角.又cos ∠BAC==-,则∠BAC=,即二面角B-PA-C的大小是.
【答案】
14. 【解析】因为=i,=-i,所以f(n)=in+(-i,利用i的周期性可以求出x=-1+i或1-i,所以共有2个元素.
【答案】2
15.(13分)
【解析】(1)因为a·b=|a||b|cos 45°=2××=2,
所以|a-b|===.
(2)因为(a+b)⊥b,所以(a+b)·b=a·b+b2=2×cos θ+2=0,
所以cos θ=-,又因为0≤θ≤π,所以θ=.
16.(15分)
【解析】(1)若z1=(-b-1)+(1-b)i为纯虚数,则,即b=-1.
(2)z2====+i.由于z1和z2互为共轭复数,所以,解得,则a+b=-1.
17.(15分)
【解析】(1)因为m·n=2sin A(cos A-sin A)-1=1-2sin2A+2sin Acos A-2=cos 2A+sin 2A-2=2cos(2A-)-2=0.由·>0,得B为钝角,则A为锐角,所以A=.
(2)因为所以b=2sin B,c=2sin C=2sin(π-B),
则b+c=2sin B+2sin(π-B)=5sin B+cos B.
而y=5sin x+cos x在(,π)上单调递减,代入值计算得118.(17分)
【解析】(1)设登山看日出组的人数为x,在海边看日落组中,高一学生、高二学生、高三学生所占的比例分别为a,b,c,则有=20%,=30%,
解得a=10%,b=30%,则c=1-10%-30%=60%.
故在海边看日落组中,高一学生、高二学生、高三学生所占的比例分别为10%,30%,60%.
(2)在海边看日落组中,高三年级应抽取的人数为80××60%=36.
19.(17分)
【解析】(1)由BC⊥AB,BC⊥AP,可知BC⊥平面PAB,则BC⊥BP,故∠PBA即为二面角P-BC-A的平面角,故∠PBA=30°,则AB=,BC=1,PC=,·=·(+)=-·=-3.
故|cos<,>|==,即直线AB与直线PC所成角的余弦值为.
(2)由PB=4PM,得点M到平面PAC的距离d等于点B到平面PAC的距离的,所以d=×=,S△PAN=×S△PAC=,
所以VP-AMN=VM-PAN=××=.
(120分钟 150分)
考试范围: 《必修第二册》第六章(20%)+第七章(10%)+第八章(25%)+第九章(45%)
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若z-2i=2+i,则|z|=()
A.2 B. C. D.
2.若向量a=(2,1),b=(0,-1),则a在b上的投影向量为()
A.(0,-1) B.(0,1) C.(2,0) D.(0,2)
3.某校高一、高二、高三年级的学生人数之比为3∶3∶4,现用分层随机抽样的方法从该校三个年级的学生中抽取容量为200的样本,则从高一年级抽取的学生人数为()
A.60 B.80 C.100 D.50
4.如图,在正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,则直线AM与BN的关系是()
A.相交
B.平行
C.异面
D.垂直
5.在平行四边形ABCD中,点E是AD的中点,点F是CD的一个三等分点(靠近点C),则=()
A.+ B.+
C.+ D.-
6.如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为正方形且边长为3,BD1与底面所成角的正切值为,则该直四棱柱的侧棱长为()
A.4
B.
C.2
D.2
7.某厂对一批产品进行抽样检测,如图所示的是抽检产品净重(单位:克)的频率分布直方图,样本数据分组为[76,78),[78,80),…,[84,86].若这批产品有200个,估计其中净重大于或等于80克的个数是()
A.110
B.140
C.150
D.90
8.已知球O的半径R为2,一母线长与圆锥底面直径相等的圆锥位于球内,圆锥顶点在球面上,底面与球面相接,则该圆锥的体积为()
A.3π B.3π C.3π D.2π
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求. 9.下列命题正确的是()
A.不共面的四点中,任意三点不共线
B.若平面α内有无数条直线与平面β垂直,则α⊥β
C.若直线a,b共面,直线a,c共面,则直线b,c共面
D.依次首尾相接的四条线段必共面
10.从某项综合能力测试中抽取100人的成绩,统计如下表,则()
分数 5 4 3 2 1
人数 30 30 20 10 10
A.这100人的成绩的平均数为3.4 B.这100人的成绩的平均数为3.6
C.这100人的成绩的方差为1.61 D.这100人的成绩的方差为1.64
11.下列说法不正确的有()
A.若z∈C,则z2≥0
B.若a>b,则a+i>b+i
C.若z1,z2∈C,且+=0,则z1=z2=0
D.若复数z满足|z|=1,则|z+2i|的最大值为3
三、填空题:本题共3小题,每小题5分,共15分.
12.在等腰△ABC中,BC=2,AB=AC,则·= .
13.如图,在三棱锥P-ABC中,PA⊥平面ABC,若AB=AC=1,BC=,则二面角B-PA-C的大小为 .
14.若f(n)=()n+((n∈N*),则集合{x|x=f(n)}中共有 个元素.
四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15.(13分)
已知|a|=2,|b|=.
(1)若a,b的夹角为45°,求|a-b|;
(2)若(a+b)⊥b,求a与b的夹角θ.
16.(15分)
已知复数z1=(-b-1)+(1-b)i,z2=,其中a,b∈R.
(1)若z1为纯虚数,求b的值;
(2)若z1与z2互为共轭复数,求a+b的值.
17.(15分)
已知向量m=(2sin A,1),n=(cos A-sin A,-1),m⊥n,其中A是△ABC的内角,· >0.
(1)求角A的大小;
(2)若角A,B,C所对的边分别为a,b,c,且a=1,求b+c的取值范围.
18.(17分)
某学校高中部最近组织了一次野外郊游活动,活动分为登山看日出组和海边看日落组,且每位学生至多参加其中一组.在参加活动的学生中,高一学生占20%,高二学生占30%,登山组的学生占参加活动的总人数的,且该组高一学生占50%,高二学生占30%.为了了解各组不同年级的学生对本次活动的满意程度,现用分层随机抽样的方法从参加活动的全体学生中抽取一个容量为80的样本.
(1)求在海边看日落组中,高一学生、高二学生、高三学生分别所占的比例;
(2)求在海边看日落组中,高三年级应抽取的人数.
19.(17分)
如图,在三棱锥P-ABC中,PA⊥底面ABC,若二面角P-BC-A的大小为30°,BC⊥AB,AC=2,PA=1,M是PB上的一点,且PB=4PM,N是PC上靠近点C的三等分点.
(1)求直线AB与直线PC所成角的余弦值;
(2)求三棱锥P-AMN的体积.
答案与解析
题序 1 2 3 4 5 6 7 8 9 10 11
答案 C B A C A D B C AB BD ABC
12. 【解析】在等腰△ABC中,BC=2,AB=AC,则·=||·||·cos(π-B)=-||2=-2.
【答案】-2
13. 【解析】因为PA⊥平面ABC,所以PA⊥AB,PA⊥AC,所以∠BAC是二面角B-PA-C的平面角.又cos ∠BAC==-,则∠BAC=,即二面角B-PA-C的大小是.
【答案】
14. 【解析】因为=i,=-i,所以f(n)=in+(-i,利用i的周期性可以求出x=-1+i或1-i,所以共有2个元素.
【答案】2
15.(13分)
【解析】(1)因为a·b=|a||b|cos 45°=2××=2,
所以|a-b|===.
(2)因为(a+b)⊥b,所以(a+b)·b=a·b+b2=2×cos θ+2=0,
所以cos θ=-,又因为0≤θ≤π,所以θ=.
16.(15分)
【解析】(1)若z1=(-b-1)+(1-b)i为纯虚数,则,即b=-1.
(2)z2====+i.由于z1和z2互为共轭复数,所以,解得,则a+b=-1.
17.(15分)
【解析】(1)因为m·n=2sin A(cos A-sin A)-1=1-2sin2A+2sin Acos A-2=cos 2A+sin 2A-2=2cos(2A-)-2=0.由·>0,得B为钝角,则A为锐角,所以A=.
(2)因为
则b+c=2sin B+2sin(π-B)=5sin B+cos B.
而y=5sin x+cos x在(,π)上单调递减,代入值计算得1
【解析】(1)设登山看日出组的人数为x,在海边看日落组中,高一学生、高二学生、高三学生所占的比例分别为a,b,c,则有=20%,=30%,
解得a=10%,b=30%,则c=1-10%-30%=60%.
故在海边看日落组中,高一学生、高二学生、高三学生所占的比例分别为10%,30%,60%.
(2)在海边看日落组中,高三年级应抽取的人数为80××60%=36.
19.(17分)
【解析】(1)由BC⊥AB,BC⊥AP,可知BC⊥平面PAB,则BC⊥BP,故∠PBA即为二面角P-BC-A的平面角,故∠PBA=30°,则AB=,BC=1,PC=,·=·(+)=-·=-3.
故|cos<,>|==,即直线AB与直线PC所成角的余弦值为.
(2)由PB=4PM,得点M到平面PAC的距离d等于点B到平面PAC的距离的,所以d=×=,S△PAN=×S△PAC=,
所以VP-AMN=VM-PAN=××=.
同课章节目录
