7.1 两个基本计数原理 同步学案(含答案)2024-2025学年高二数学苏教版(2019)选择性必修第二册
文档属性
| 名称 | 7.1 两个基本计数原理 同步学案(含答案)2024-2025学年高二数学苏教版(2019)选择性必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 252.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-26 23:47:35 | ||
图片预览



文档简介
7.1 两个基本计数原理
7.1.1 两个基本计数原理(1)
1. 准确理解分类计数原理和分步计数原理,弄清它们的区别.
2. 会运用分类计数原理和分步计数原理解决一些简单的问题.
活动一 背景引入
背景1:小王要从上海到北京旅游,有三种交通工具可供选择:长途汽车、旅客列车、飞机.若每天长途汽车有2班,旅客列车有 3班,飞机有2班.问共有多少种不同的走法?
思考1
(1) 从上海到北京按不同的交通工具可分几类出行方式?
(2) 每一类方式中分别有几种不同的班次选择?则完成这件事共有多少种不同的走法?
(3) 每类方式中的每一种方法有什么特征?
背景2:小王要从上海到北京旅游,若想途中到天津参观南开大学,已知从上海到天津有3种走法,从天津到北京有4种走法.问要从上海经过天津到北京共有多少种不同的走法?
思考2
(1) 从上海经过天津到北京有几个步骤?
(2) 每一步中分别有几种走法?则完成这件事共有多少种走法?
(3) 上述每步的每种方法能否单独实现从上海经过天津到北京的目的?
思考3
(1) 上述两个背景问题有什么区别?
(2) 由这两个问题分别可以得到怎样的数学模型?
(3) 如何用数学语言表述以上数学模型的结论?
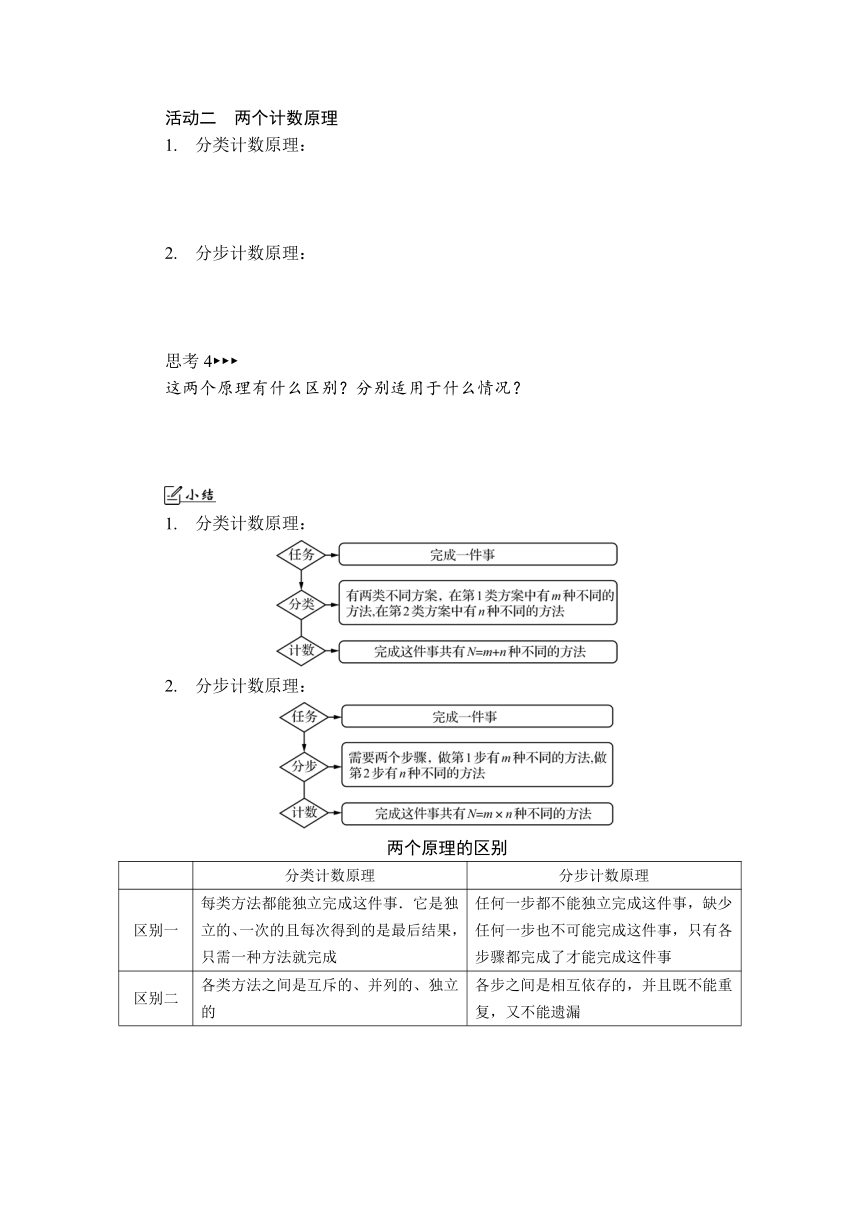
活动二 两个计数原理
1. 分类计数原理:
2. 分步计数原理:
思考4
这两个原理有什么区别?分别适用于什么情况?
1. 分类计数原理:
2. 分步计数原理:
两个原理的区别
分类计数原理 分步计数原理
区别一 每类方法都能独立完成这件事.它是独立的、一次的且每次得到的是最后结果,只需一种方法就完成 任何一步都不能独立完成这件事,缺少任何一步也不可能完成这件事,只有各步骤都完成了才能完成这件事
区别二 各类方法之间是互斥的、并列的、独立的 各步之间是相互依存的,并且既不能重复,又不能遗漏
活动三 两个原理的简单应用
例1 某班共有男生28名、女生20名,从该班选出学生代表参加校学生代表大会.
(1) 若学校分配给该班1名代表,则有多少种不同的选法?
(2) 若学校分配给该班2名代表,且男、女生代表各1名,则有多少种不同的选法?
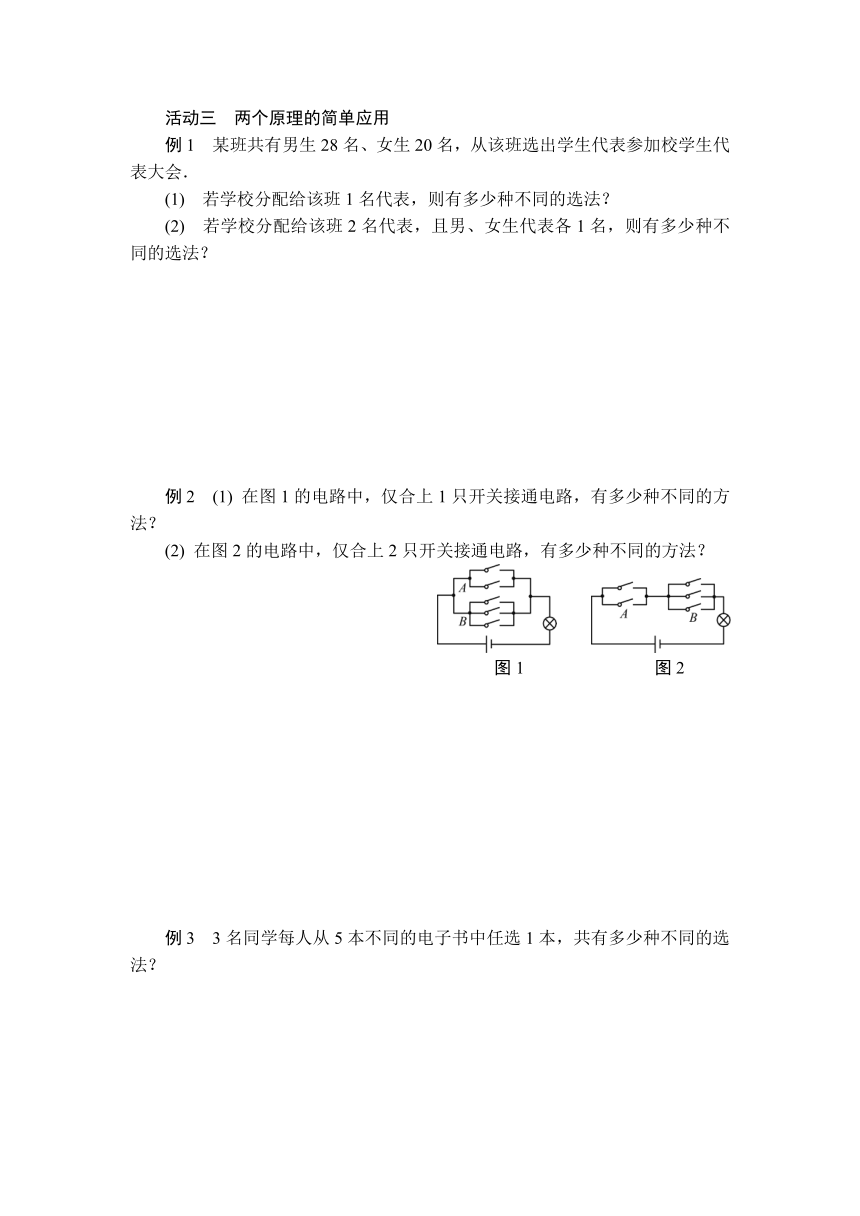
例2 (1) 在图1的电路中,仅合上1只开关接通电路,有多少种不同的方法?
(2) 在图2的电路中,仅合上2只开关接通电路,有多少种不同的方法?
图1 图2
例3 3名同学每人从5本不同的电子书中任选1本,共有多少种不同的选法?
1. (教材改编)从甲地出发前往乙地,一天中有4趟汽车、3趟火车和1趟航班可供选择.某人某天要从甲地出发,去乙地旅游,则所有不同走法的种数为( )
A. 16 B. 15 C. 12 D. 8
2. (2024大同月考)现有3名老师、6名男同学和4名女同学共13人.若需1名老师和1名学生参加评选会议,则不同的选法种数为( )
A. 30 B. 18 C. 12 D. 13
3. (多选)(2023沈阳月考)下列结论中,正确的是( )
A. 在分类计数原理中,两类不同方案中的方法可以相同
B. 在分类计数原理中,每类方案中的方法都能直接完成这件事
C. 在分步计数原理中,事情是分步完成的,其中任何一个单独的步骤都不能完成这件事,只有每个步骤都完成后,这件事情才算完成
D. 在分步计数原理中,每个步骤中完成这个步骤的方法可以相同
4. (教材改编)用1,5,9,13中的任意一个数作分子,4,8,12,16中任意一个数作分母,可以构成________个不同的真分数.
5. 某医院现有3名医生、5名护士、2名麻醉师.
(1) 从中选派1名外出参加学习,有多少种不同的选法?
(2) 从这些人中选出1名医生,1名护士和1名麻醉师组成1个医疗小组,有多少种不同的选法?
7.1.2 两个基本计数原理(2)
1. 巩固分类计数原理和分步计数原理,能正确进行“分类”与“分步”.
2. 综合运用分类计数原理和分步计数原理解决复杂的问题.
活动一 复习巩固
1. 两个基本计数原理的内容:
2. 两个基本计数原理的区别及适用情形:
练习1 从甲地到乙地一天有汽车 8班,火车3班,轮船2班,则某人一天内乘坐不同班次的汽车、火车或轮船到乙地时,共有______种不同的走法.
练习2 为了给某种新品种农作物选择最佳的生产条件,在分别有4种土质、2种不同的施肥量、3种不同的种植密度、2种不同的播种时间的因素下进行种植试验,则共有______种不同的试验方案.
活动二 掌握分类标准的确定方法
例1 在所有两位数中,个位数字大于十位数字的两位数共有多少个?
思考1
如何确定分类的标准?
三边长均为整数,且最大边长为11的三角形的个数是多少?
在1~20共20个整数中取2个数相加,使其和为偶数的不同取法共有多少种?
活动三 掌握分步标准的确定方法
例2 5名学生报名参加四项体育比赛,每人限报一项,报名方法的种数为多少?若他们争夺这四项比赛的冠军,则获得冠军的可能的种数为多少?(每个比赛项目只有一个冠军)
思考2
如何确定分步的标准?
从-1,0,1,2这四个数中选三个不同的数作为函数f(x)=ax2+bx+c的系数,可组成不同的二次函数共有________个,其中不同的偶函数共有________个.
活动四 掌握两个原理的综合应用
例3 为了确保电子邮箱的安全,在注册时,通常要设置电子邮箱密码.在某网站设置的邮箱中,
(1) 若密码为4位,每位均为0~9这10个数字中的1个,则这样的密码共有多少个?
(2) 若密码为4~6位,每位均为0~9这10个数字中的1个,则这样的密码共有多少个?
有0,1,2,3,4五个数字.
(1) 可以排出多少个三位数字的电话号码?
(2) 可以排成多少个三位数?
(3) 可以排成多少个能被2整除的无重复数字的三位数?
1. 已知集合M={1,-2,3},N={-4,5,6,-7},从两个集合中各取1个元素作为点的坐标,则在平面直角坐标系中,第一、二象限不同点的个数为( )
A. 18 B. 16 C. 14 D. 10
2. (教材改编)地图涂色是一类经典的数学问题.如图,用4种不同的颜色涂所给图形中的4个区域,要求相邻区域的颜色不能相同,则不同的涂色方法有( )
A. 84种 B. 72种
C. 48种 D. 24种
3. (多选)(2024山东月考)有6名同学参加3个智力竞赛项目,则下列说法中正确的是( )
A. 若每人报名参加一项,每项的人数不限,则共有729种不同的报名方案
B. 若每人报名参加一项,每项的人数不限,则共有216种不同的报名方案
C. 每项只报一人,每人报名参加的项目不限,则共有216种不同的报名方案
D. 每项只报一人,且每人至多报名参加一项,则共有120种不同的报名方案
4. 若集合A∪B={1,2,3},则集合A,B共有________种组合.
5. 在300和800之间,有多少个没有重复数字的奇数?
7.1 两个基本计数原理
7.1.1 两个基本计数原理(1)
【活动方案】
思考1:(1) 分为长途汽车、旅客列车、飞机三类.
(2) 长途汽车有2班,旅客列车有3班,飞机有2班.完成这件事共有2+3+2=7(种)不同的走法.
(3) 每类方式中的每一种方法都能达到完成这件事的目的.
思考2:(1) 先从上海到天津,再从天津到北京,有两个步骤.
(2) 从上海到天津有3种走法,从天津到北京有 4种走法,则完成这件事共有3×4=12(种)走法.
(3) 不能,必须依次连续完成两个步骤才能实现从上海经过天津到北京的目的.
思考3:(1) 背景1是分类完成一件事,背景2是分步完成一件事.
(2) 分类计数原理,分步计数原理.
(3) 如果完成一件事有n类方式,这n类方式彼此间独立,不论哪一类方式中的哪一种方法都能单独完成这件事,那么求完成这件事的方法种数就用分类计数原理;如果完成一件事需分成n个步骤依次连续完成,而完成每一个步骤各有若干种方法,那么求完成这件事的方法种数就用分步计数原理.
1. 如果完成一件事,有n类方式,在第1类方式中有m1种不同的方法,在第2类方式中有m2种不同的方法,…,在第n类方式中有mn种不同的方法,那么完成这件事共有N=m1+m2+…+mn种不同的方法.
2. 如果完成一件事,需要分成n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,…,做第n步有mn种不同的方法,那么完成这件事共有N=m1×m2×…×mn种不同的方法.
思考4:分类计数原理关键在于分类,并且每类方法都能独立地完成这件事;分步计数原理关键在于分步,必须连续完成各个步骤后才算完成这件事.
例1 (1) 选出1名代表有两类方式:第一类,从男生中选出1名代表,有28种不同的选法;第二类,从女生中选出1名代表,有20种不同的选法.根据分类计数原理,共有不同的选法种数是28+20=48.
(2) 选出男、女生代表各1名,可以分两个步骤完成:第一步,选1名男生代表,有28种不同的选法;第二步,选1名女生代表,有20种不同的选法.根据分步计数原理,选出男、女生代表各1名,共有不同的选法种数是28×20=560.
例2 (1) 在图1中,按要求接通电路,只要在A中的 2只开关或B中的3只开关中合上1只即可.根据分类计数原理,共有2+3=5(种)不同的方法.
(2) 在图2中,按要求接通电路必须分两步进行:第一步,合上A中的1只开关;第二步,合上B中的 1只开关.根据分步计数原理,共有2×3=6(种)不同的方法.
例3 第一名同学选1本电子书有5种不同的选法,第二、第三名同学各选1本电子书,仍各有5种不同的选法.因此,根据分步计数原理,3名同学每人各选1本电子书的不同选法种数是5×5×5=125.
【检测反馈】
1. D 根据分类计数原理,可知共有不同的走法种数为4+3+1=8.
2. A 先从3名老师中任选1名,有3种选法,再从10名学生中任选1名,有10种选法.由分步计数原理知,共有不同的选法种数为3×10=30.
3. BC 对于A,在分类计数原理中,两类不同方案中的方法互不相同,故A错误;对于B,在分类计数原理中,每类方案中的方法都能直接完成这件事,故B正确;对于C,在分步计数原理中,事情是分步完成的,其中任何一个单独的步骤都不能完成这件事,只有每个步骤都完成后,这件事情才算完成,故C正确;对于D,在分步计数原理中,每个步骤中完成这个步骤的方法是各不相同的,故D错误.故选BC.
4. 10 由真分数的定义,①若1为分子,分母有4种选择;②若5为分子,分母有3种选择;③若9为分子,分母有2种选择;④若13为分子,分母有1种选择,所以可以构成不同的真分数共有4+3+2+1=10(个).
5. (1) 分三类:第一类:选出的是医生,共有3种选法;
第二类:选出的是护士,共有5种选法;
第三类:选出的是麻醉师,共有2种选法.
根据分类计数原理,共有不同的选法种数为3+5+2=10.
(2) 分三步:第一步:选出1名医生,共有3种选法;
第二步:选出1名护士,共有5种选法;
第三步:选出1名麻醉师,共有2种选法.
根据分步计数原理,共有不同的选法种数为3×5×2=30.
7.1.2 两个基本计数原理(2)
【活动方案】
1. 略
2. 略
练习1:13 根据分类计数原理,共有不同的走法种数为8+3+2=13.
练习2:48 根据分步计数原理,不同的试验方案种数为4×2×3×2=48.
例1 因为个位数字大于十位数字,所以按个位数字是2,3,4,5,6,7,8,9分为8类,在每一类中满足题意的两位数中分别有1个,2个,3个,4个,5个,6个,7个,8个,根据分类计数原理,符合题意的两位数的个数为1+2+3+4+5+6+7+8=36.
思考1:根据问题的性质确定分类的标准,如例1中可按个位数字或十位数字分类.
跟踪训练1 设三角形另外两边的长分别为x,y,x∈N*,y∈N*,且 x≤y,则
当x=1时,y=11;当x=2时,y=10或y=11;当 x=3时,y=9或y=10或y=11;…;当x=11时,y=11,
所以根据分类计数原理,不同的三角形的个数为 1+2+3+4+5+6+5+4+3+2+1=36.
跟踪训练2 第一类:偶数和偶数相加,由分步计数原理,得共有=45(种)取法;第二类:奇数和奇数相加,由分步计数原理,得共有=45(种)取法.根据分类计数原理,不同的取法共有45+45=90(种).
例2 5名学生每人报名的方法都为4种,根据分步计数原理,报名方法的种数为4×4×4×4×4=1 024.获得第一项比赛的冠军有5种可能,则获得第二项比赛的冠军有4种可能,获得第三项比赛的冠军有3种可能,获得第四项比赛的冠军有2种可能,根据分步计数原理,获得冠军的可能的种数为5×4×3×2=120.
思考2:根据问题发生的过程确定分步的标准.
跟踪训练 18 6 a的选法有3个,b的选法有3个,c的选法有2个,根据分步计数原理,共有 3×3×2=18(个)不同的二次函数;当函数为偶函数时,b=0,则a的选法有3个,c的选法有2个,根据分步计数原理,其中不同的偶函数的个数为3×2=6.
例3 (1) 设置1个4位密码要分4步进行,每一步确定一位数字,每一位上都可以从0~9这10个数字中任取1个,有10种取法.根据分步计数原理,4位密码的个数是10×10×10×10=10 000.
(2) 设置的密码为4~6位,每位均为0~9这10个数字中的1个,这样的密码共有3类.其中4位密码、5位密码、6位密码的个数分别为104,105,106.根据分类计数原理,设置由数字0~9组成的4~6位密码的个数是104+105+106=1 110 000.
跟踪训练 (1) 三位数字的电话号码,首位可以是0,数字也可以重复,每个位置都有5种选法,共有5×5×5=53=125(个).
(2) 三位数的首位不能为0,但可以有重复数字,首先考虑首位的选法,除0外共有4种选法,第二、三位可以排0,因此共有4×5×5=100(个).
(3) 被2整除的数即偶数,末位数字可取0,2,4,因此可以分两类,第一类是末位数字是0,则有4×3=12(种)选法;第二类是末位数字不是0,则末位有2种选法,即2或4,再排首位,因为0不能在首位,所以有3种选法,十位有3种选法,因此有2×3×3=18(种)选法,所以共有12+18=30(种)选法,即可以排成30个能被2整除的无重复数字的三位数.
【检测反馈】
1. C 分两类:一是以集合M中的元素为横坐标,以集合N中的元素为纵坐标,有3×2=6(个)不同的点;二是以集合N中的元素为横坐标,以集合M中的元素为纵坐标,有4×2=8(个)不同的点,故由分类计数原理得共有6+8=14(个)不同的点.
2. A 将图形区域分为上下左右,若上下颜色相同,则上有4种,左有3种,右有3种,共有4×3×3=36(种);若上下颜色不同,则上有4种,下有3种,左右各有两种,共有4×3×2×2=48(种),所以共有36+48=84(种).
3. ACD 对于A,B,按照6名同学参加的项目,分为6步,每步均有3种选择,根据分步计数原理可知,共有36=729(种)不同的报名方案,故A正确,B错误;对于C,根据3个智力竞赛项目,分为3步,每步均有6种选择,根据分步计数原理可知,共有63=216(种)不同的报名方案,故C正确;对于D,根据3个智力竞赛项目,分为3步.第1步有6种选择;第2步有5种选择;第3步有4种选择.根据分步计数原理可知,共有6×5×4=120(种)不同的报名方案,故D正确.故选ACD.
4. 27 当集合A为空集时,集合B={1,2,3},有1种;当集合A包含1个元素时,例如A={1},则集合B可以为{1,2,3}或{2,3},故有3×2=6(种);当集合A包含2个元素时,例如A={1,2},则集合B可以为{1,2,3},{1,3},{2,3},{3},故有3×4=12(种);当集合A包含3个元素时,例如A={1,2,3},则集合B可以没有元素,1个元素,2个元素,3个元素,故有1+3+3+1=8(种).根据分类计数原理可得,共有1+6+12+8=27(种).
5. 一个三位奇数的个位上的数字必是奇数,且因为不允许有重复数字出现,当一个奇数字(1,3,5,7,9)作为个位数时,它就不能作为百位数,所以符合条件的数可以按百位上的数字是奇数或偶数分成两类:
第一类:百位上的数字是偶数.这样的三位数可以由以下三个步骤确定:
第一步,百位上的数字从4和6中任选一个,有2种选法:
第二步,个位上的数字从1,3,5,7,9中任选一个,有5种选法;
第三步,十位上的数字从余下的8个数字中任选一个,有8种选法.
根据乘法原理,这一类奇数的个数为2×5×8=80.
第二类:百位上的数字是奇数.这样的三位数可以由以下三个步骤确定:
第一步,百位上的数字从3,5,7中任选一个,有3种选法;
第二步,个位上的数字从余下的4个奇数中任选一个,有4种选法;
第三步,十位上的数字从余下的8个数字中任选一个,有8种选法.
根据乘法原理,这一类奇数的个数为3×4×8=96.
根据加法原理,在300和800之间共有80+96=176(个)没有重复数字的奇数.
7.1.1 两个基本计数原理(1)
1. 准确理解分类计数原理和分步计数原理,弄清它们的区别.
2. 会运用分类计数原理和分步计数原理解决一些简单的问题.
活动一 背景引入
背景1:小王要从上海到北京旅游,有三种交通工具可供选择:长途汽车、旅客列车、飞机.若每天长途汽车有2班,旅客列车有 3班,飞机有2班.问共有多少种不同的走法?
思考1
(1) 从上海到北京按不同的交通工具可分几类出行方式?
(2) 每一类方式中分别有几种不同的班次选择?则完成这件事共有多少种不同的走法?
(3) 每类方式中的每一种方法有什么特征?
背景2:小王要从上海到北京旅游,若想途中到天津参观南开大学,已知从上海到天津有3种走法,从天津到北京有4种走法.问要从上海经过天津到北京共有多少种不同的走法?
思考2
(1) 从上海经过天津到北京有几个步骤?
(2) 每一步中分别有几种走法?则完成这件事共有多少种走法?
(3) 上述每步的每种方法能否单独实现从上海经过天津到北京的目的?
思考3
(1) 上述两个背景问题有什么区别?
(2) 由这两个问题分别可以得到怎样的数学模型?
(3) 如何用数学语言表述以上数学模型的结论?
活动二 两个计数原理
1. 分类计数原理:
2. 分步计数原理:
思考4
这两个原理有什么区别?分别适用于什么情况?
1. 分类计数原理:
2. 分步计数原理:
两个原理的区别
分类计数原理 分步计数原理
区别一 每类方法都能独立完成这件事.它是独立的、一次的且每次得到的是最后结果,只需一种方法就完成 任何一步都不能独立完成这件事,缺少任何一步也不可能完成这件事,只有各步骤都完成了才能完成这件事
区别二 各类方法之间是互斥的、并列的、独立的 各步之间是相互依存的,并且既不能重复,又不能遗漏
活动三 两个原理的简单应用
例1 某班共有男生28名、女生20名,从该班选出学生代表参加校学生代表大会.
(1) 若学校分配给该班1名代表,则有多少种不同的选法?
(2) 若学校分配给该班2名代表,且男、女生代表各1名,则有多少种不同的选法?
例2 (1) 在图1的电路中,仅合上1只开关接通电路,有多少种不同的方法?
(2) 在图2的电路中,仅合上2只开关接通电路,有多少种不同的方法?
图1 图2
例3 3名同学每人从5本不同的电子书中任选1本,共有多少种不同的选法?
1. (教材改编)从甲地出发前往乙地,一天中有4趟汽车、3趟火车和1趟航班可供选择.某人某天要从甲地出发,去乙地旅游,则所有不同走法的种数为( )
A. 16 B. 15 C. 12 D. 8
2. (2024大同月考)现有3名老师、6名男同学和4名女同学共13人.若需1名老师和1名学生参加评选会议,则不同的选法种数为( )
A. 30 B. 18 C. 12 D. 13
3. (多选)(2023沈阳月考)下列结论中,正确的是( )
A. 在分类计数原理中,两类不同方案中的方法可以相同
B. 在分类计数原理中,每类方案中的方法都能直接完成这件事
C. 在分步计数原理中,事情是分步完成的,其中任何一个单独的步骤都不能完成这件事,只有每个步骤都完成后,这件事情才算完成
D. 在分步计数原理中,每个步骤中完成这个步骤的方法可以相同
4. (教材改编)用1,5,9,13中的任意一个数作分子,4,8,12,16中任意一个数作分母,可以构成________个不同的真分数.
5. 某医院现有3名医生、5名护士、2名麻醉师.
(1) 从中选派1名外出参加学习,有多少种不同的选法?
(2) 从这些人中选出1名医生,1名护士和1名麻醉师组成1个医疗小组,有多少种不同的选法?
7.1.2 两个基本计数原理(2)
1. 巩固分类计数原理和分步计数原理,能正确进行“分类”与“分步”.
2. 综合运用分类计数原理和分步计数原理解决复杂的问题.
活动一 复习巩固
1. 两个基本计数原理的内容:
2. 两个基本计数原理的区别及适用情形:
练习1 从甲地到乙地一天有汽车 8班,火车3班,轮船2班,则某人一天内乘坐不同班次的汽车、火车或轮船到乙地时,共有______种不同的走法.
练习2 为了给某种新品种农作物选择最佳的生产条件,在分别有4种土质、2种不同的施肥量、3种不同的种植密度、2种不同的播种时间的因素下进行种植试验,则共有______种不同的试验方案.
活动二 掌握分类标准的确定方法
例1 在所有两位数中,个位数字大于十位数字的两位数共有多少个?
思考1
如何确定分类的标准?
三边长均为整数,且最大边长为11的三角形的个数是多少?
在1~20共20个整数中取2个数相加,使其和为偶数的不同取法共有多少种?
活动三 掌握分步标准的确定方法
例2 5名学生报名参加四项体育比赛,每人限报一项,报名方法的种数为多少?若他们争夺这四项比赛的冠军,则获得冠军的可能的种数为多少?(每个比赛项目只有一个冠军)
思考2
如何确定分步的标准?
从-1,0,1,2这四个数中选三个不同的数作为函数f(x)=ax2+bx+c的系数,可组成不同的二次函数共有________个,其中不同的偶函数共有________个.
活动四 掌握两个原理的综合应用
例3 为了确保电子邮箱的安全,在注册时,通常要设置电子邮箱密码.在某网站设置的邮箱中,
(1) 若密码为4位,每位均为0~9这10个数字中的1个,则这样的密码共有多少个?
(2) 若密码为4~6位,每位均为0~9这10个数字中的1个,则这样的密码共有多少个?
有0,1,2,3,4五个数字.
(1) 可以排出多少个三位数字的电话号码?
(2) 可以排成多少个三位数?
(3) 可以排成多少个能被2整除的无重复数字的三位数?
1. 已知集合M={1,-2,3},N={-4,5,6,-7},从两个集合中各取1个元素作为点的坐标,则在平面直角坐标系中,第一、二象限不同点的个数为( )
A. 18 B. 16 C. 14 D. 10
2. (教材改编)地图涂色是一类经典的数学问题.如图,用4种不同的颜色涂所给图形中的4个区域,要求相邻区域的颜色不能相同,则不同的涂色方法有( )
A. 84种 B. 72种
C. 48种 D. 24种
3. (多选)(2024山东月考)有6名同学参加3个智力竞赛项目,则下列说法中正确的是( )
A. 若每人报名参加一项,每项的人数不限,则共有729种不同的报名方案
B. 若每人报名参加一项,每项的人数不限,则共有216种不同的报名方案
C. 每项只报一人,每人报名参加的项目不限,则共有216种不同的报名方案
D. 每项只报一人,且每人至多报名参加一项,则共有120种不同的报名方案
4. 若集合A∪B={1,2,3},则集合A,B共有________种组合.
5. 在300和800之间,有多少个没有重复数字的奇数?
7.1 两个基本计数原理
7.1.1 两个基本计数原理(1)
【活动方案】
思考1:(1) 分为长途汽车、旅客列车、飞机三类.
(2) 长途汽车有2班,旅客列车有3班,飞机有2班.完成这件事共有2+3+2=7(种)不同的走法.
(3) 每类方式中的每一种方法都能达到完成这件事的目的.
思考2:(1) 先从上海到天津,再从天津到北京,有两个步骤.
(2) 从上海到天津有3种走法,从天津到北京有 4种走法,则完成这件事共有3×4=12(种)走法.
(3) 不能,必须依次连续完成两个步骤才能实现从上海经过天津到北京的目的.
思考3:(1) 背景1是分类完成一件事,背景2是分步完成一件事.
(2) 分类计数原理,分步计数原理.
(3) 如果完成一件事有n类方式,这n类方式彼此间独立,不论哪一类方式中的哪一种方法都能单独完成这件事,那么求完成这件事的方法种数就用分类计数原理;如果完成一件事需分成n个步骤依次连续完成,而完成每一个步骤各有若干种方法,那么求完成这件事的方法种数就用分步计数原理.
1. 如果完成一件事,有n类方式,在第1类方式中有m1种不同的方法,在第2类方式中有m2种不同的方法,…,在第n类方式中有mn种不同的方法,那么完成这件事共有N=m1+m2+…+mn种不同的方法.
2. 如果完成一件事,需要分成n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法,…,做第n步有mn种不同的方法,那么完成这件事共有N=m1×m2×…×mn种不同的方法.
思考4:分类计数原理关键在于分类,并且每类方法都能独立地完成这件事;分步计数原理关键在于分步,必须连续完成各个步骤后才算完成这件事.
例1 (1) 选出1名代表有两类方式:第一类,从男生中选出1名代表,有28种不同的选法;第二类,从女生中选出1名代表,有20种不同的选法.根据分类计数原理,共有不同的选法种数是28+20=48.
(2) 选出男、女生代表各1名,可以分两个步骤完成:第一步,选1名男生代表,有28种不同的选法;第二步,选1名女生代表,有20种不同的选法.根据分步计数原理,选出男、女生代表各1名,共有不同的选法种数是28×20=560.
例2 (1) 在图1中,按要求接通电路,只要在A中的 2只开关或B中的3只开关中合上1只即可.根据分类计数原理,共有2+3=5(种)不同的方法.
(2) 在图2中,按要求接通电路必须分两步进行:第一步,合上A中的1只开关;第二步,合上B中的 1只开关.根据分步计数原理,共有2×3=6(种)不同的方法.
例3 第一名同学选1本电子书有5种不同的选法,第二、第三名同学各选1本电子书,仍各有5种不同的选法.因此,根据分步计数原理,3名同学每人各选1本电子书的不同选法种数是5×5×5=125.
【检测反馈】
1. D 根据分类计数原理,可知共有不同的走法种数为4+3+1=8.
2. A 先从3名老师中任选1名,有3种选法,再从10名学生中任选1名,有10种选法.由分步计数原理知,共有不同的选法种数为3×10=30.
3. BC 对于A,在分类计数原理中,两类不同方案中的方法互不相同,故A错误;对于B,在分类计数原理中,每类方案中的方法都能直接完成这件事,故B正确;对于C,在分步计数原理中,事情是分步完成的,其中任何一个单独的步骤都不能完成这件事,只有每个步骤都完成后,这件事情才算完成,故C正确;对于D,在分步计数原理中,每个步骤中完成这个步骤的方法是各不相同的,故D错误.故选BC.
4. 10 由真分数的定义,①若1为分子,分母有4种选择;②若5为分子,分母有3种选择;③若9为分子,分母有2种选择;④若13为分子,分母有1种选择,所以可以构成不同的真分数共有4+3+2+1=10(个).
5. (1) 分三类:第一类:选出的是医生,共有3种选法;
第二类:选出的是护士,共有5种选法;
第三类:选出的是麻醉师,共有2种选法.
根据分类计数原理,共有不同的选法种数为3+5+2=10.
(2) 分三步:第一步:选出1名医生,共有3种选法;
第二步:选出1名护士,共有5种选法;
第三步:选出1名麻醉师,共有2种选法.
根据分步计数原理,共有不同的选法种数为3×5×2=30.
7.1.2 两个基本计数原理(2)
【活动方案】
1. 略
2. 略
练习1:13 根据分类计数原理,共有不同的走法种数为8+3+2=13.
练习2:48 根据分步计数原理,不同的试验方案种数为4×2×3×2=48.
例1 因为个位数字大于十位数字,所以按个位数字是2,3,4,5,6,7,8,9分为8类,在每一类中满足题意的两位数中分别有1个,2个,3个,4个,5个,6个,7个,8个,根据分类计数原理,符合题意的两位数的个数为1+2+3+4+5+6+7+8=36.
思考1:根据问题的性质确定分类的标准,如例1中可按个位数字或十位数字分类.
跟踪训练1 设三角形另外两边的长分别为x,y,x∈N*,y∈N*,且 x≤y,则
当x=1时,y=11;当x=2时,y=10或y=11;当 x=3时,y=9或y=10或y=11;…;当x=11时,y=11,
所以根据分类计数原理,不同的三角形的个数为 1+2+3+4+5+6+5+4+3+2+1=36.
跟踪训练2 第一类:偶数和偶数相加,由分步计数原理,得共有=45(种)取法;第二类:奇数和奇数相加,由分步计数原理,得共有=45(种)取法.根据分类计数原理,不同的取法共有45+45=90(种).
例2 5名学生每人报名的方法都为4种,根据分步计数原理,报名方法的种数为4×4×4×4×4=1 024.获得第一项比赛的冠军有5种可能,则获得第二项比赛的冠军有4种可能,获得第三项比赛的冠军有3种可能,获得第四项比赛的冠军有2种可能,根据分步计数原理,获得冠军的可能的种数为5×4×3×2=120.
思考2:根据问题发生的过程确定分步的标准.
跟踪训练 18 6 a的选法有3个,b的选法有3个,c的选法有2个,根据分步计数原理,共有 3×3×2=18(个)不同的二次函数;当函数为偶函数时,b=0,则a的选法有3个,c的选法有2个,根据分步计数原理,其中不同的偶函数的个数为3×2=6.
例3 (1) 设置1个4位密码要分4步进行,每一步确定一位数字,每一位上都可以从0~9这10个数字中任取1个,有10种取法.根据分步计数原理,4位密码的个数是10×10×10×10=10 000.
(2) 设置的密码为4~6位,每位均为0~9这10个数字中的1个,这样的密码共有3类.其中4位密码、5位密码、6位密码的个数分别为104,105,106.根据分类计数原理,设置由数字0~9组成的4~6位密码的个数是104+105+106=1 110 000.
跟踪训练 (1) 三位数字的电话号码,首位可以是0,数字也可以重复,每个位置都有5种选法,共有5×5×5=53=125(个).
(2) 三位数的首位不能为0,但可以有重复数字,首先考虑首位的选法,除0外共有4种选法,第二、三位可以排0,因此共有4×5×5=100(个).
(3) 被2整除的数即偶数,末位数字可取0,2,4,因此可以分两类,第一类是末位数字是0,则有4×3=12(种)选法;第二类是末位数字不是0,则末位有2种选法,即2或4,再排首位,因为0不能在首位,所以有3种选法,十位有3种选法,因此有2×3×3=18(种)选法,所以共有12+18=30(种)选法,即可以排成30个能被2整除的无重复数字的三位数.
【检测反馈】
1. C 分两类:一是以集合M中的元素为横坐标,以集合N中的元素为纵坐标,有3×2=6(个)不同的点;二是以集合N中的元素为横坐标,以集合M中的元素为纵坐标,有4×2=8(个)不同的点,故由分类计数原理得共有6+8=14(个)不同的点.
2. A 将图形区域分为上下左右,若上下颜色相同,则上有4种,左有3种,右有3种,共有4×3×3=36(种);若上下颜色不同,则上有4种,下有3种,左右各有两种,共有4×3×2×2=48(种),所以共有36+48=84(种).
3. ACD 对于A,B,按照6名同学参加的项目,分为6步,每步均有3种选择,根据分步计数原理可知,共有36=729(种)不同的报名方案,故A正确,B错误;对于C,根据3个智力竞赛项目,分为3步,每步均有6种选择,根据分步计数原理可知,共有63=216(种)不同的报名方案,故C正确;对于D,根据3个智力竞赛项目,分为3步.第1步有6种选择;第2步有5种选择;第3步有4种选择.根据分步计数原理可知,共有6×5×4=120(种)不同的报名方案,故D正确.故选ACD.
4. 27 当集合A为空集时,集合B={1,2,3},有1种;当集合A包含1个元素时,例如A={1},则集合B可以为{1,2,3}或{2,3},故有3×2=6(种);当集合A包含2个元素时,例如A={1,2},则集合B可以为{1,2,3},{1,3},{2,3},{3},故有3×4=12(种);当集合A包含3个元素时,例如A={1,2,3},则集合B可以没有元素,1个元素,2个元素,3个元素,故有1+3+3+1=8(种).根据分类计数原理可得,共有1+6+12+8=27(种).
5. 一个三位奇数的个位上的数字必是奇数,且因为不允许有重复数字出现,当一个奇数字(1,3,5,7,9)作为个位数时,它就不能作为百位数,所以符合条件的数可以按百位上的数字是奇数或偶数分成两类:
第一类:百位上的数字是偶数.这样的三位数可以由以下三个步骤确定:
第一步,百位上的数字从4和6中任选一个,有2种选法:
第二步,个位上的数字从1,3,5,7,9中任选一个,有5种选法;
第三步,十位上的数字从余下的8个数字中任选一个,有8种选法.
根据乘法原理,这一类奇数的个数为2×5×8=80.
第二类:百位上的数字是奇数.这样的三位数可以由以下三个步骤确定:
第一步,百位上的数字从3,5,7中任选一个,有3种选法;
第二步,个位上的数字从余下的4个奇数中任选一个,有4种选法;
第三步,十位上的数字从余下的8个数字中任选一个,有8种选法.
根据乘法原理,这一类奇数的个数为3×4×8=96.
根据加法原理,在300和800之间共有80+96=176(个)没有重复数字的奇数.
