9.1.1 变量的相关性 同步学案(含答案) 2024-2025学年高二数学苏教版(2019)选择性必修第二册
文档属性
| 名称 | 9.1.1 变量的相关性 同步学案(含答案) 2024-2025学年高二数学苏教版(2019)选择性必修第二册 |

|
|
| 格式 | docx | ||
| 文件大小 | 175.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-26 23:49:45 | ||
图片预览


文档简介
9.1.1 变量的相关性
1. 通过实例了解变量的相关关系,能根据生活经验判断变量之间的相关性.
2. 了解散点图的概念,并能用散点图直观判断变量之间的相关关系.
3. 了解线性相关关系,并能用散点图判断变量之间的线性相关关系.
4. 了解正相关、负相关等概念,会用散点图进行判断.
5. 结合实例,会通过相关系数比较多组成对数据的相关性.
活动一 变量间的相关关系
思考1
圆的面积与半径之间的关系是什么关系?球的体积与半径之间的关系又是什么关系?
思考2
人的脚长与身高、农作物的产量与施肥量、家庭的收入与支出,可以分别用一个关系式表示吗?
相关关系的定义:两个变量之间具有一定的联系,但又没有确定性函数关系,相对于确定的自变量,因变量的取值具有随机性的变量之间的关系通常称之为相关关系.
例1 试判断下列各个问题中两个变量之间是否具有相关关系:
(1) 商品的销售价格与其供应量;
(2) 汽车的耗油量与行驶速度;
(3) 真空中自由降落的小球的位移(单位:m)与时间(单位:s);
(4) 空气中污染物浓度(单位:μg/m3)与日降雨量(单位:cm).
下列关系中,属于相关关系的是________.(填序号)
①正方形的边长与面积之间的关系;
②人的年龄与他(她)拥有的学识之间的关系;
③出租车费与行驶的里程;
④降雪量与交通事故的发生率之间的关系.
活动二 线性相关关系
在相关关系中,因变量的值不能随自变量的值的确定而确定,所以无法直接用函数去描述变量之间的这种关系.我们都是用“直觉”与“经验”进行推断,具有粗略、不够精确的特点,如何进行更为科学、严密的推断呢?
我们需要借助数据说话,即通过样本数据分析,从数据中提取信息,并建构适当的模型,再利用模型进行估计或推断.
全国城镇居民人均年可支配收入与人均年支出(单位:元)的部分数据(来源:《中国统计年鉴(2016)》)如下表所示.
年份 1990 2000 2010 2011 2012 2013 2014 2015
人均年可支配收入 1 510 6 280 19 109 21 810 24 565 26 467 28 844 31 195
人均年支出 1 279 4 998 13 471 15 161 16 674 18 488 19 968 21 392
你能得出什么结论?
线性相关关系的定义:在散点图中,可以看出点落在某条直线的附近,我们将具有这种特性的相关关系称为线性相关关系.如果这些散点呈从左下向右上方向发展的趋势,我们称这两个变量之间正相关;如果这些散点呈从左上向右下方向发展的趋势,我们称这两个变量之间负相关.
例2 有几组变量:①汽车的质量和汽车每消耗1 L汽油所行驶的平均路程;②平均日学习时间和平均学习成绩;③立方体的棱长和体积.其中两个变量之间正相关的是( )
A. ①③ B. ②③ C. ② D. ③
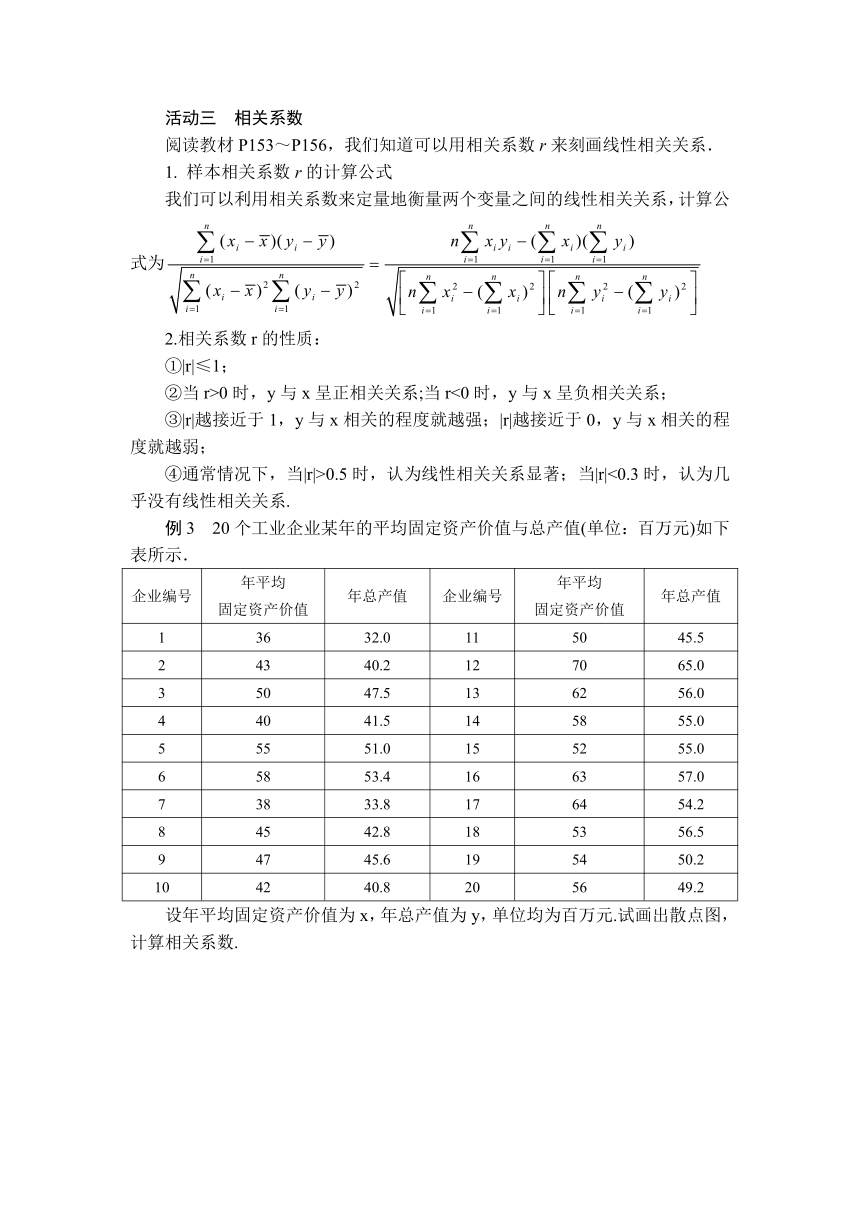
活动三 相关系数
阅读教材P153~P156,我们知道可以用相关系数r来刻画线性相关关系.
1. 样本相关系数r的计算公式
我们可以利用相关系数来定量地衡量两个变量之间的线性相关关系,计算公式为
2.相关系数r的性质:
①|r|≤1;
②当r>0时,y与x呈正相关关系;当r<0时,y与x呈负相关关系;
③|r|越接近于1,y与x相关的程度就越强;|r|越接近于0,y与x相关的程度就越弱;
④通常情况下,当|r|>0.5时,认为线性相关关系显著;当|r|<0.3时,认为几乎没有线性相关关系.
例3 20个工业企业某年的平均固定资产价值与总产值(单位:百万元)如下表所示.
企业编号 年平均 固定资产价值 年总产值 企业编号 年平均 固定资产价值 年总产值
1 36 32.0 11 50 45.5
2 43 40.2 12 70 65.0
3 50 47.5 13 62 56.0
4 40 41.5 14 58 55.0
5 55 51.0 15 52 55.0
6 58 53.4 16 63 57.0
7 38 33.8 17 64 54.2
8 45 42.8 18 53 56.5
9 47 45.6 19 54 50.2
10 42 40.8 20 56 49.2
设年平均固定资产价值为x,年总产值为y,单位均为百万元.试画出散点图,计算相关系数.
对两个变量x,y进行线性相关检验,得线性相关系数r1=0.785 9,对两个变量u,v进行线性相关检验,得线性相关系数r2=-0.9568,则下列结论中正确的是( )
变量x与y正相关,变量u与v负相关,变量x与y的线性相关性较强
变量x与y负相关,变量u与v正相关,变量x与y的线性相关性较强
变量x与y正相关,变量u与o负相关,变量u与v的线性相关性较强
变量x与y负相关,变量u与o正相关,变量u与v的线性相关性较强
下列语句所表示的事件中的因素不具有相关关系的是( )
瑞雪兆丰年
读书破万卷,下笔如有神
吸烟有害健康
喜鹊叫喜,乌鸦叫丧
某超市统计了最近5年的商品销售额与利润率数据,经计算相关系数r=0.862,则下列结论中正确的是( )
商品销售额与利润率正相关,且具有较弱的相关关系
商品销售额与利润率正相关,且具有较强的相关关系.
商品销售额与利润率负相关,且具有较弱的相关关系
商品销售额与利润率负相关,且具有较强的相关关系
3. (多选)(2024 江苏月考)下列说法中,正确的是( )
A. 闯红灯与交通事故发生率的关系是相关关系
B. 同一物体的加速度与作用力是函数关系
C. 产品的成本与产量之间的关系是函数关系
D. 广告费用与销售量之间的关系是相关关系
4. 已知两个变量x,y的一组观测数据如下表所示.
x 8 10 12 14 16
y 6 7.5 7.8 9.2 10.8
则根据数据可以判断x,y 相关关系. (填“有”或“无")
有一位同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出热饮杯数与当天气温的对比表:
温度/℃ -5 0 4 7 12 15
热饮杯数 156 150 132 128 130 116
温度/℃ 19 23 27 31 36
热饮杯数 104 89 93 76 54
(1)画出散点图;
(2)你能从散点图中发现气温与热饮销售杯数之间关系的一般规律吗
9.1.1 变量的相关性
【活动方案】
思考1:S=πr2,V=R3.
思考2:一般来说,人的脚长与身高有关,农作物的产量与施肥量有关,家庭的收入与支出有一定关系,但这些不能用一个函数来表示.
例1 (1) 商品的销售价格与其供应量之间具有相关关系.一般来说,在品质相当的情况下,供应量越大,价格就越低;供应量越小,价格就越高.某些品牌商品限量供应,就是保持较高价位的销售策略.
(2) 汽车的耗油量与行驶速度之间具有相关关系.通常情况下,当速度很慢或速度很快时,耗油较多,而在中等车速(不同的汽车范围不一定一样)时,速度稍高,耗油反而较少.
(3) 根据自由落体运动方程,自由降落的小球的位移与时间之间是函数关系.
(4) 空气中污染物浓度与日降雨量之间具有相关关系.通常情况下,降雨量越大,空气中污染物浓度就越低.
跟踪训练 ②④ 在①中,正方形的边长与面积之间的关系是函数关系;在②中,一般地,人的年龄与他(她)拥有的学识之间具有相关关系;在③中,出租车费与行驶的里程之间的关系是函数关系;在④中,降雪量与交通事故的发生率之间具有相关关系.
背景引入:由题意,得人均年支出与人均年可支配收入的大致关系也可用图来表示.我们以横坐标x表示人均年可支配收入,纵坐标y表示人均年支出,建立平面直角坐标系,将表中数据构成的8个点在坐标系内标出,得到下图.我们称这类图为散点图.
通过散点图可以看出,随着人均年可支配收入的增加,人均年支出也在提高,这8个点散布在一条直线附近,说明人均年支出y与人均年可支配收入x具有相关关系.
例2 C ①是负相关;②是正相关;③不是相关关系.
例3 散点图如下图所示.
根据r=,
可得相关系数为r≈0.939 6.
因此,y与x有着很强的正相关关系.
跟踪训练 C 由线性相关系数r1=0.785 9>0,得x与y呈正相关,由线性相关系数r2=-0.956 8<0,得u与v呈负相关.又<,所以变量u与v的线性相关性比x与y的线性相关性强.
【检测反馈】
1. D “瑞雪兆丰年”和“读书破万卷,下笔如有神”是根据多年经验总结归纳出来的,吸烟有害健康具有科学根据,所以它们都具有相关关系;结合生活经验知喜鹊和乌鸦发出叫声是它们自身的生理反应,与人无任何关系,故D项不具有相关关系.
2. B 因为r=0.862>0,所以商品销售额与利润率呈正相关.又r=0.862接近1,所以具有较强的相关关系.
3. ABD 闯红灯与发生交通事故之间不是因果关系,但具有相关性,是相关关系,故A正确;物体的加速度与作用力的关系是函数关系,故B正确;产品的成本与产量之间是相关关系,故C错误;广告费用与销售量之间是相关关系,故D正确.故选ABD.
4. 有 x由小变大时,y也由小变大,因此,两个变量有相关关系.
5. (1) 以x轴表示温度,y轴表示热饮杯数,可作散点图如图.
(2) 从图中可以看出,这些点散布在一条直线附近,因此,气温与热饮销售杯数之间具有相关关系.这些点呈从左上逐渐向右下方向发展的趋势,即气温越高,卖出去的热饮杯数越少.
1. 通过实例了解变量的相关关系,能根据生活经验判断变量之间的相关性.
2. 了解散点图的概念,并能用散点图直观判断变量之间的相关关系.
3. 了解线性相关关系,并能用散点图判断变量之间的线性相关关系.
4. 了解正相关、负相关等概念,会用散点图进行判断.
5. 结合实例,会通过相关系数比较多组成对数据的相关性.
活动一 变量间的相关关系
思考1
圆的面积与半径之间的关系是什么关系?球的体积与半径之间的关系又是什么关系?
思考2
人的脚长与身高、农作物的产量与施肥量、家庭的收入与支出,可以分别用一个关系式表示吗?
相关关系的定义:两个变量之间具有一定的联系,但又没有确定性函数关系,相对于确定的自变量,因变量的取值具有随机性的变量之间的关系通常称之为相关关系.
例1 试判断下列各个问题中两个变量之间是否具有相关关系:
(1) 商品的销售价格与其供应量;
(2) 汽车的耗油量与行驶速度;
(3) 真空中自由降落的小球的位移(单位:m)与时间(单位:s);
(4) 空气中污染物浓度(单位:μg/m3)与日降雨量(单位:cm).
下列关系中,属于相关关系的是________.(填序号)
①正方形的边长与面积之间的关系;
②人的年龄与他(她)拥有的学识之间的关系;
③出租车费与行驶的里程;
④降雪量与交通事故的发生率之间的关系.
活动二 线性相关关系
在相关关系中,因变量的值不能随自变量的值的确定而确定,所以无法直接用函数去描述变量之间的这种关系.我们都是用“直觉”与“经验”进行推断,具有粗略、不够精确的特点,如何进行更为科学、严密的推断呢?
我们需要借助数据说话,即通过样本数据分析,从数据中提取信息,并建构适当的模型,再利用模型进行估计或推断.
全国城镇居民人均年可支配收入与人均年支出(单位:元)的部分数据(来源:《中国统计年鉴(2016)》)如下表所示.
年份 1990 2000 2010 2011 2012 2013 2014 2015
人均年可支配收入 1 510 6 280 19 109 21 810 24 565 26 467 28 844 31 195
人均年支出 1 279 4 998 13 471 15 161 16 674 18 488 19 968 21 392
你能得出什么结论?
线性相关关系的定义:在散点图中,可以看出点落在某条直线的附近,我们将具有这种特性的相关关系称为线性相关关系.如果这些散点呈从左下向右上方向发展的趋势,我们称这两个变量之间正相关;如果这些散点呈从左上向右下方向发展的趋势,我们称这两个变量之间负相关.
例2 有几组变量:①汽车的质量和汽车每消耗1 L汽油所行驶的平均路程;②平均日学习时间和平均学习成绩;③立方体的棱长和体积.其中两个变量之间正相关的是( )
A. ①③ B. ②③ C. ② D. ③
活动三 相关系数
阅读教材P153~P156,我们知道可以用相关系数r来刻画线性相关关系.
1. 样本相关系数r的计算公式
我们可以利用相关系数来定量地衡量两个变量之间的线性相关关系,计算公式为
2.相关系数r的性质:
①|r|≤1;
②当r>0时,y与x呈正相关关系;当r<0时,y与x呈负相关关系;
③|r|越接近于1,y与x相关的程度就越强;|r|越接近于0,y与x相关的程度就越弱;
④通常情况下,当|r|>0.5时,认为线性相关关系显著;当|r|<0.3时,认为几乎没有线性相关关系.
例3 20个工业企业某年的平均固定资产价值与总产值(单位:百万元)如下表所示.
企业编号 年平均 固定资产价值 年总产值 企业编号 年平均 固定资产价值 年总产值
1 36 32.0 11 50 45.5
2 43 40.2 12 70 65.0
3 50 47.5 13 62 56.0
4 40 41.5 14 58 55.0
5 55 51.0 15 52 55.0
6 58 53.4 16 63 57.0
7 38 33.8 17 64 54.2
8 45 42.8 18 53 56.5
9 47 45.6 19 54 50.2
10 42 40.8 20 56 49.2
设年平均固定资产价值为x,年总产值为y,单位均为百万元.试画出散点图,计算相关系数.
对两个变量x,y进行线性相关检验,得线性相关系数r1=0.785 9,对两个变量u,v进行线性相关检验,得线性相关系数r2=-0.9568,则下列结论中正确的是( )
变量x与y正相关,变量u与v负相关,变量x与y的线性相关性较强
变量x与y负相关,变量u与v正相关,变量x与y的线性相关性较强
变量x与y正相关,变量u与o负相关,变量u与v的线性相关性较强
变量x与y负相关,变量u与o正相关,变量u与v的线性相关性较强
下列语句所表示的事件中的因素不具有相关关系的是( )
瑞雪兆丰年
读书破万卷,下笔如有神
吸烟有害健康
喜鹊叫喜,乌鸦叫丧
某超市统计了最近5年的商品销售额与利润率数据,经计算相关系数r=0.862,则下列结论中正确的是( )
商品销售额与利润率正相关,且具有较弱的相关关系
商品销售额与利润率正相关,且具有较强的相关关系.
商品销售额与利润率负相关,且具有较弱的相关关系
商品销售额与利润率负相关,且具有较强的相关关系
3. (多选)(2024 江苏月考)下列说法中,正确的是( )
A. 闯红灯与交通事故发生率的关系是相关关系
B. 同一物体的加速度与作用力是函数关系
C. 产品的成本与产量之间的关系是函数关系
D. 广告费用与销售量之间的关系是相关关系
4. 已知两个变量x,y的一组观测数据如下表所示.
x 8 10 12 14 16
y 6 7.5 7.8 9.2 10.8
则根据数据可以判断x,y 相关关系. (填“有”或“无")
有一位同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出热饮杯数与当天气温的对比表:
温度/℃ -5 0 4 7 12 15
热饮杯数 156 150 132 128 130 116
温度/℃ 19 23 27 31 36
热饮杯数 104 89 93 76 54
(1)画出散点图;
(2)你能从散点图中发现气温与热饮销售杯数之间关系的一般规律吗
9.1.1 变量的相关性
【活动方案】
思考1:S=πr2,V=R3.
思考2:一般来说,人的脚长与身高有关,农作物的产量与施肥量有关,家庭的收入与支出有一定关系,但这些不能用一个函数来表示.
例1 (1) 商品的销售价格与其供应量之间具有相关关系.一般来说,在品质相当的情况下,供应量越大,价格就越低;供应量越小,价格就越高.某些品牌商品限量供应,就是保持较高价位的销售策略.
(2) 汽车的耗油量与行驶速度之间具有相关关系.通常情况下,当速度很慢或速度很快时,耗油较多,而在中等车速(不同的汽车范围不一定一样)时,速度稍高,耗油反而较少.
(3) 根据自由落体运动方程,自由降落的小球的位移与时间之间是函数关系.
(4) 空气中污染物浓度与日降雨量之间具有相关关系.通常情况下,降雨量越大,空气中污染物浓度就越低.
跟踪训练 ②④ 在①中,正方形的边长与面积之间的关系是函数关系;在②中,一般地,人的年龄与他(她)拥有的学识之间具有相关关系;在③中,出租车费与行驶的里程之间的关系是函数关系;在④中,降雪量与交通事故的发生率之间具有相关关系.
背景引入:由题意,得人均年支出与人均年可支配收入的大致关系也可用图来表示.我们以横坐标x表示人均年可支配收入,纵坐标y表示人均年支出,建立平面直角坐标系,将表中数据构成的8个点在坐标系内标出,得到下图.我们称这类图为散点图.
通过散点图可以看出,随着人均年可支配收入的增加,人均年支出也在提高,这8个点散布在一条直线附近,说明人均年支出y与人均年可支配收入x具有相关关系.
例2 C ①是负相关;②是正相关;③不是相关关系.
例3 散点图如下图所示.
根据r=,
可得相关系数为r≈0.939 6.
因此,y与x有着很强的正相关关系.
跟踪训练 C 由线性相关系数r1=0.785 9>0,得x与y呈正相关,由线性相关系数r2=-0.956 8<0,得u与v呈负相关.又<,所以变量u与v的线性相关性比x与y的线性相关性强.
【检测反馈】
1. D “瑞雪兆丰年”和“读书破万卷,下笔如有神”是根据多年经验总结归纳出来的,吸烟有害健康具有科学根据,所以它们都具有相关关系;结合生活经验知喜鹊和乌鸦发出叫声是它们自身的生理反应,与人无任何关系,故D项不具有相关关系.
2. B 因为r=0.862>0,所以商品销售额与利润率呈正相关.又r=0.862接近1,所以具有较强的相关关系.
3. ABD 闯红灯与发生交通事故之间不是因果关系,但具有相关性,是相关关系,故A正确;物体的加速度与作用力的关系是函数关系,故B正确;产品的成本与产量之间是相关关系,故C错误;广告费用与销售量之间是相关关系,故D正确.故选ABD.
4. 有 x由小变大时,y也由小变大,因此,两个变量有相关关系.
5. (1) 以x轴表示温度,y轴表示热饮杯数,可作散点图如图.
(2) 从图中可以看出,这些点散布在一条直线附近,因此,气温与热饮销售杯数之间具有相关关系.这些点呈从左上逐渐向右下方向发展的趋势,即气温越高,卖出去的热饮杯数越少.
