第9章统计 同步学案(含答案)2024-2025学年高二数学苏教版(2019)选择性必修第二册
文档属性
| 名称 | 第9章统计 同步学案(含答案)2024-2025学年高二数学苏教版(2019)选择性必修第二册 |
|
|
| 格式 | docx | ||
| 文件大小 | 197.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-26 23:57:28 | ||
图片预览




文档简介
第9章 统计
1. 会求线性回归方程,并运用回归直线进行预测.
2. 理解独立性检验的基本思想及实施步骤.
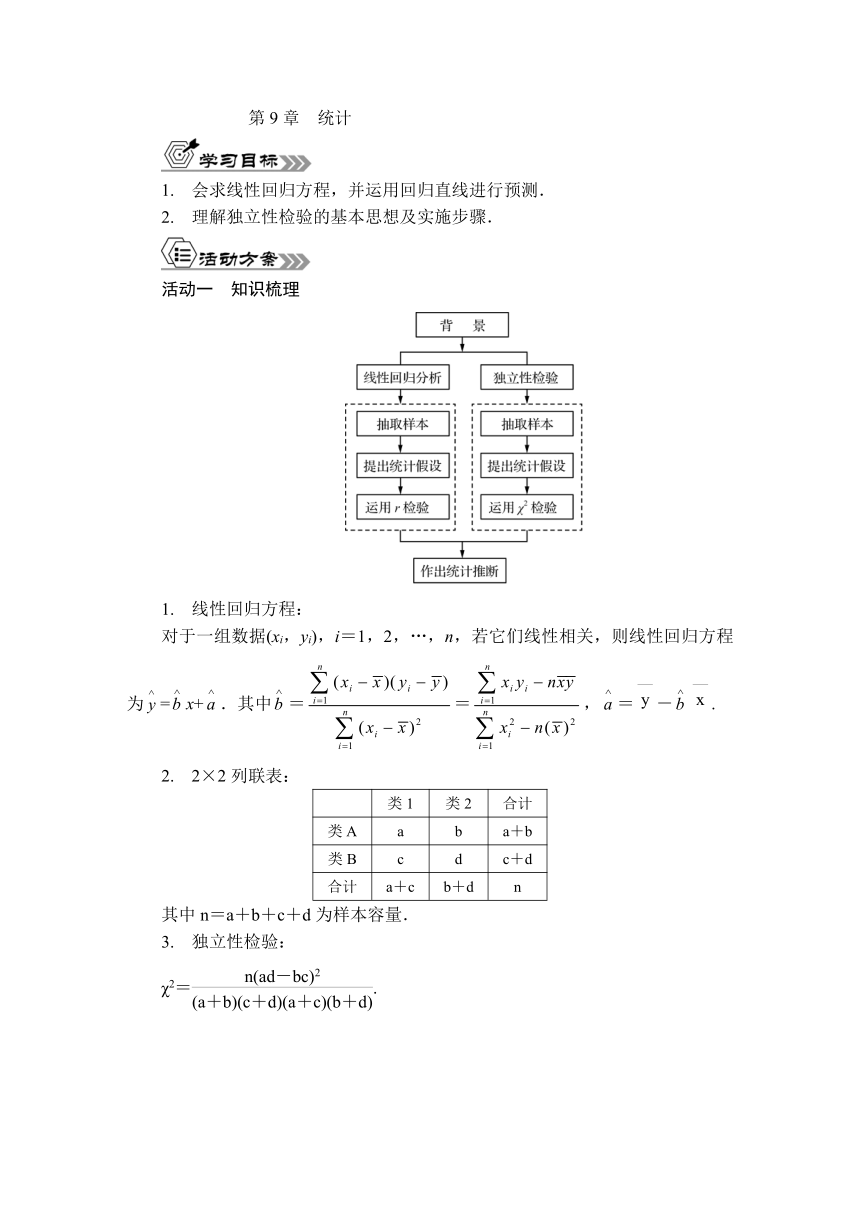
活动一 知识梳理
1. 线性回归方程:
对于一组数据(xi,yi),i=1,2,…,n,若它们线性相关,则线性回归方程为=x+.其中==,=-.
2. 2×2列联表:
类1 类2 合计
类A a b a+b
类B c d c+d
合计 a+c b+d n
其中n=a+b+c+d为样本容量.
3. 独立性检验:
χ2=.
活动二 线性回归分析
例1 (2024曲靖月考)某地区响应“节能减排,低碳生活”的号召,开展一系列的措施控制碳排放.环保部门收集到近5年内新增碳排放数量,如下表所示,其中x为年份代号,y(单位:万吨)代表新增碳排放量.
年份 2019 2020 2021 2022 2023
年份代号x 1 2 3 4 5
新增碳排放量y/万吨 6.1 5.2 4.9 4 3.8
(1) 请计算并用相关系数r的数值说明x与y之间的线性相关性的强弱(保留小数点后两位);
(2) 求y关于x的线性回归方程,并据此估计该地区2024年的新增碳排放数量.
参考数据:=66.2,=118.7,≈1.87,≈5.92.
参考公式:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线的斜率和截距的最小二乘估计公式,相关系数r的公式分别为=,=-,r=.
活动三 独立性检验
例2 奥运会期间,为调查某高校学生是否愿意提供志愿者服务,用简单随机抽样方法从该校调查了60人,结果如下:
愿意 不愿意
男生 20 10
女生 10 20
(1) 用分层抽样的方法在愿意提供志愿者服务的学生中抽取6人,其中男生抽取多少人?
(2) 能否在犯错误的概率不超过0.01的前提下,认为该校高中生是否愿意提供志愿者服务与性别有关?
参考数据及公式:
P(χ2≥x0) 0.15 0.10 0.05 0.025 0.010 0.005 0.001
x0 2.072 2.706 3.841 5.024 6.635 7.879 10.828
χ2=,其中n=a+b+c+d.
1. (2024辽宁月考)已知具有线性相关的两个变量x,y之间的一组数据如表:
x -2 -1 1 2 3
y 24 36 40 48 56
且线性回归方程为=5.5x+,则当x=4时,y的预测值为( )
A. 59.5 B. 60.5
C. 61.5 D. 62.5
2. (2023德州期末)随着国家对中小学“双减”政策的逐步落实,其中增加中学生体育锻炼时间的政策引发社会的广泛关注.某教育时报为研究“支持增加中学生体育锻炼时间的政策是否与性别有关”,从某校男女生中各随机抽取80名学生进行问卷调查,得到如下数据(10≤m≤20,m∈N* ):
支持 不支持
男生 70-m 10+m
女生 50+m 30-m
通过计算有95%以上的把握认为“支持增加中学生体育锻炼时间的政策与性别有关”,则在这被调查的80名女生中支持增加中学生体育锻炼时间的人数的最小值为( )
附:χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.100 0.050 0.010 0.005 0.001
x0 2.706 3.841 6.635 7.879 10.828
A. 15 B. 65 C. 16 D. 66
3. (多选)(2024大连期中)下列结论中,正确的是( )
A. 以模型y=cekx去拟合一组数据时,为了求出回归方程,设z=ln y,将其变换后得到线性方程z=0.3x+4,则c,k的值分别是e4和0.3
B. 在线性回归方程=-0.8x+3中,当变量x每增加1个单位时,减少0.8个单位
C. 在回归模型中,残差平方和越小,说明模型的拟合程度越好
D. 对分类变量X和Y来说,它们的统计量χ2的观测值x0越大,“X与Y有关系”的把握程度越小
4. (2024昆明期中)盲盒里面通常装的是动漫、影视作品的周边,或者设计师单独设计出来的玩偶.由于盒子上没有标注,购买者只有打开才会知道自己买到了什么,因此这种惊喜吸引了众多年轻人,形成了“盲盒经济”.某销售网点为了调查购买该款盲盒是否与性别有关,得到如下2×2列联表:
女生 男生 合计
购买 40 20 60
未购买 70 70 140
合计 110 90 200
则认为是否购买该款盲盒与性别有关出错的可能性为________.
附:χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.10 0.05 0.025 0.010 0.005 0.001
x0 2.706 3.841 5.024 6.635 7.879 10.828
5. (2024温州期中)为了解高中学生每天课后自主学习数学时间x(单位:min)和他们的数学成绩y(单位:分)的关系,某实验小组做了调查,得到一些数据如下:
编号 1 2 3 4 5
学习时间x 30 40 50 60 70
数学成绩y 65 78 85 99 108
(1) 求数学成绩y与学习时间x的相关系数(精确到0.001);
(2) 请用相关系数说明该组数据中y与x之间的关系可用线性回归模型进行拟合,并求出y关于x的线性回归方程,并由此预测每天课后自主学习数学时间为100 min时的数学成绩(参考数据:=22 820,=435,=38 999,≈107.4,xi(i=1,2,…,5)的方差为200);
(3) 基于上述调查,某校提倡学生周末在校自主学习.经过一学期的实施后,抽样调查了220位学生.按照是否参与周末在校自主学习以及成绩是否有进步统计,得到2×2列联表如下:
没有进步 有进步 合计
参与周末在校自主学习 35 130 165
未参与周末在校自主学习 25 30 55
合计 60 160 220
依据表中的数据,是否有99.9%的把握认为学生周末在校自主学习与成绩进步有关.
附:==,=-,
r==,
χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.10 0.05 0.010 0.005 0.001
x0 2.706 3.841 6.635 7.879 10.828
第9章 统 计
【活动方案】
例1 (1) 由题意,得==3,
==4.8,
=12+22+32+42+52=55,
r=
=
=
==≈≈-0.98,
因为|r|≈0.98,所以x与y的线性相关程度很强.
(2) ====-0.58,
=-=4.8+0.58×3=6.54,
所以=-0.58x+6.54,
当x=6时,=-0.58×6+6.54=3.06(万吨).
故估计该地区2024年的新增碳排放数量为3.06万吨.
例2 (1) 由题意,得男生抽取6×=4(人).
(2) χ2=≈6.667,
因为6.667>6.635,所以能在犯错误的概率不超过0.01的前提下认为该校高中生是否愿意提供志愿者服务与性别有关.
【检测反馈】
1. A ==0.6,==40.8,所以=-5.5×=40.8-5.5×0.6=37.5,所以=5.5x+37.5,故当x=4时,y的预测值为5.5×4+37.5=59.5.
2. D 因为有95%以上的把握认为“支持增加中学生体育锻炼时间的政策与性别有关”,所以>3.841,即(m-10)2>28.807 5.因为当10≤m≤20时,函数y=(m-10)2单调递增,且m∈N*, (15-10)2<28.807 5,(16-10)2>28.807 5,所以m的最小值为16,所以在这被调查的80名女生中支持增加中学生体育锻炼时间的人数的最小值为50+16=66.
3. ABC 对于A,y=cekx,两边取对数,得ln y=ln (cekx)=ln c+ln ekx,则z=ln c+kx.因为z=0.3x+4,所以ln c=4,k=0.3,c=e4,故A正确;对于B,在线性回归方程=-0.8x+3中,当变量x每增加1个单位时,减少0.8个单位,故B正确;对于C,在回归模型中,残差平方和越小,说明模型的拟合程度越好,故C正确;对于D,对分类变量X和Y来说,它们的统计量χ2的观测值x0越大,“X与Y有关系”的把握程度越大,故D错误.故选ABC.
4. 5% 因为χ2=≈4.714>3.841,故认为是否购买该款盲盒与性别有关出错的可能性为5%.
5. (1) 由题意,得==50,==87,(xi-)2=200×5=1 000,所以r==≈≈0.996.
(2) 由(1)知,r≈0.996接近1,
所以y与x之间具有极强的线性相关关系,
故可用线性回归模型进行拟合.
又===1.07,
=-=87-1.07×50=33.5,
所以=1.07x+33.5,
当x=100时,=1.07×100+33.5=140.5,
故预测每天课后自主学习数学时间为100 min时的数学成绩为140.5分.
(3) 提出假设H0:学生周末在校自主学习与成绩进步无关.
根据数据,计算,得
χ2==≈12.22.
因为12.22>10.828,
所以有99.9%的把握认为学生周末在校自主学习与成绩进步有关.
1. 会求线性回归方程,并运用回归直线进行预测.
2. 理解独立性检验的基本思想及实施步骤.
活动一 知识梳理
1. 线性回归方程:
对于一组数据(xi,yi),i=1,2,…,n,若它们线性相关,则线性回归方程为=x+.其中==,=-.
2. 2×2列联表:
类1 类2 合计
类A a b a+b
类B c d c+d
合计 a+c b+d n
其中n=a+b+c+d为样本容量.
3. 独立性检验:
χ2=.
活动二 线性回归分析
例1 (2024曲靖月考)某地区响应“节能减排,低碳生活”的号召,开展一系列的措施控制碳排放.环保部门收集到近5年内新增碳排放数量,如下表所示,其中x为年份代号,y(单位:万吨)代表新增碳排放量.
年份 2019 2020 2021 2022 2023
年份代号x 1 2 3 4 5
新增碳排放量y/万吨 6.1 5.2 4.9 4 3.8
(1) 请计算并用相关系数r的数值说明x与y之间的线性相关性的强弱(保留小数点后两位);
(2) 求y关于x的线性回归方程,并据此估计该地区2024年的新增碳排放数量.
参考数据:=66.2,=118.7,≈1.87,≈5.92.
参考公式:对于一组数据(x1,y1),(x2,y2),…,(xn,yn),其回归直线的斜率和截距的最小二乘估计公式,相关系数r的公式分别为=,=-,r=.
活动三 独立性检验
例2 奥运会期间,为调查某高校学生是否愿意提供志愿者服务,用简单随机抽样方法从该校调查了60人,结果如下:
愿意 不愿意
男生 20 10
女生 10 20
(1) 用分层抽样的方法在愿意提供志愿者服务的学生中抽取6人,其中男生抽取多少人?
(2) 能否在犯错误的概率不超过0.01的前提下,认为该校高中生是否愿意提供志愿者服务与性别有关?
参考数据及公式:
P(χ2≥x0) 0.15 0.10 0.05 0.025 0.010 0.005 0.001
x0 2.072 2.706 3.841 5.024 6.635 7.879 10.828
χ2=,其中n=a+b+c+d.
1. (2024辽宁月考)已知具有线性相关的两个变量x,y之间的一组数据如表:
x -2 -1 1 2 3
y 24 36 40 48 56
且线性回归方程为=5.5x+,则当x=4时,y的预测值为( )
A. 59.5 B. 60.5
C. 61.5 D. 62.5
2. (2023德州期末)随着国家对中小学“双减”政策的逐步落实,其中增加中学生体育锻炼时间的政策引发社会的广泛关注.某教育时报为研究“支持增加中学生体育锻炼时间的政策是否与性别有关”,从某校男女生中各随机抽取80名学生进行问卷调查,得到如下数据(10≤m≤20,m∈N* ):
支持 不支持
男生 70-m 10+m
女生 50+m 30-m
通过计算有95%以上的把握认为“支持增加中学生体育锻炼时间的政策与性别有关”,则在这被调查的80名女生中支持增加中学生体育锻炼时间的人数的最小值为( )
附:χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.100 0.050 0.010 0.005 0.001
x0 2.706 3.841 6.635 7.879 10.828
A. 15 B. 65 C. 16 D. 66
3. (多选)(2024大连期中)下列结论中,正确的是( )
A. 以模型y=cekx去拟合一组数据时,为了求出回归方程,设z=ln y,将其变换后得到线性方程z=0.3x+4,则c,k的值分别是e4和0.3
B. 在线性回归方程=-0.8x+3中,当变量x每增加1个单位时,减少0.8个单位
C. 在回归模型中,残差平方和越小,说明模型的拟合程度越好
D. 对分类变量X和Y来说,它们的统计量χ2的观测值x0越大,“X与Y有关系”的把握程度越小
4. (2024昆明期中)盲盒里面通常装的是动漫、影视作品的周边,或者设计师单独设计出来的玩偶.由于盒子上没有标注,购买者只有打开才会知道自己买到了什么,因此这种惊喜吸引了众多年轻人,形成了“盲盒经济”.某销售网点为了调查购买该款盲盒是否与性别有关,得到如下2×2列联表:
女生 男生 合计
购买 40 20 60
未购买 70 70 140
合计 110 90 200
则认为是否购买该款盲盒与性别有关出错的可能性为________.
附:χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.10 0.05 0.025 0.010 0.005 0.001
x0 2.706 3.841 5.024 6.635 7.879 10.828
5. (2024温州期中)为了解高中学生每天课后自主学习数学时间x(单位:min)和他们的数学成绩y(单位:分)的关系,某实验小组做了调查,得到一些数据如下:
编号 1 2 3 4 5
学习时间x 30 40 50 60 70
数学成绩y 65 78 85 99 108
(1) 求数学成绩y与学习时间x的相关系数(精确到0.001);
(2) 请用相关系数说明该组数据中y与x之间的关系可用线性回归模型进行拟合,并求出y关于x的线性回归方程,并由此预测每天课后自主学习数学时间为100 min时的数学成绩(参考数据:=22 820,=435,=38 999,≈107.4,xi(i=1,2,…,5)的方差为200);
(3) 基于上述调查,某校提倡学生周末在校自主学习.经过一学期的实施后,抽样调查了220位学生.按照是否参与周末在校自主学习以及成绩是否有进步统计,得到2×2列联表如下:
没有进步 有进步 合计
参与周末在校自主学习 35 130 165
未参与周末在校自主学习 25 30 55
合计 60 160 220
依据表中的数据,是否有99.9%的把握认为学生周末在校自主学习与成绩进步有关.
附:==,=-,
r==,
χ2=,其中n=a+b+c+d.
P(χ2≥x0) 0.10 0.05 0.010 0.005 0.001
x0 2.706 3.841 6.635 7.879 10.828
第9章 统 计
【活动方案】
例1 (1) 由题意,得==3,
==4.8,
=12+22+32+42+52=55,
r=
=
=
==≈≈-0.98,
因为|r|≈0.98,所以x与y的线性相关程度很强.
(2) ====-0.58,
=-=4.8+0.58×3=6.54,
所以=-0.58x+6.54,
当x=6时,=-0.58×6+6.54=3.06(万吨).
故估计该地区2024年的新增碳排放数量为3.06万吨.
例2 (1) 由题意,得男生抽取6×=4(人).
(2) χ2=≈6.667,
因为6.667>6.635,所以能在犯错误的概率不超过0.01的前提下认为该校高中生是否愿意提供志愿者服务与性别有关.
【检测反馈】
1. A ==0.6,==40.8,所以=-5.5×=40.8-5.5×0.6=37.5,所以=5.5x+37.5,故当x=4时,y的预测值为5.5×4+37.5=59.5.
2. D 因为有95%以上的把握认为“支持增加中学生体育锻炼时间的政策与性别有关”,所以>3.841,即(m-10)2>28.807 5.因为当10≤m≤20时,函数y=(m-10)2单调递增,且m∈N*, (15-10)2<28.807 5,(16-10)2>28.807 5,所以m的最小值为16,所以在这被调查的80名女生中支持增加中学生体育锻炼时间的人数的最小值为50+16=66.
3. ABC 对于A,y=cekx,两边取对数,得ln y=ln (cekx)=ln c+ln ekx,则z=ln c+kx.因为z=0.3x+4,所以ln c=4,k=0.3,c=e4,故A正确;对于B,在线性回归方程=-0.8x+3中,当变量x每增加1个单位时,减少0.8个单位,故B正确;对于C,在回归模型中,残差平方和越小,说明模型的拟合程度越好,故C正确;对于D,对分类变量X和Y来说,它们的统计量χ2的观测值x0越大,“X与Y有关系”的把握程度越大,故D错误.故选ABC.
4. 5% 因为χ2=≈4.714>3.841,故认为是否购买该款盲盒与性别有关出错的可能性为5%.
5. (1) 由题意,得==50,==87,(xi-)2=200×5=1 000,所以r==≈≈0.996.
(2) 由(1)知,r≈0.996接近1,
所以y与x之间具有极强的线性相关关系,
故可用线性回归模型进行拟合.
又===1.07,
=-=87-1.07×50=33.5,
所以=1.07x+33.5,
当x=100时,=1.07×100+33.5=140.5,
故预测每天课后自主学习数学时间为100 min时的数学成绩为140.5分.
(3) 提出假设H0:学生周末在校自主学习与成绩进步无关.
根据数据,计算,得
χ2==≈12.22.
因为12.22>10.828,
所以有99.9%的把握认为学生周末在校自主学习与成绩进步有关.
