7.3.2 离散型随机变量的方差 同步学案(含答案) 2024~2025学年高二数学人教A版(2019)选择性必修3
文档属性
| 名称 | 7.3.2 离散型随机变量的方差 同步学案(含答案) 2024~2025学年高二数学人教A版(2019)选择性必修3 |

|
|
| 格式 | docx | ||
| 文件大小 | 108.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-26 23:54:11 | ||
图片预览


文档简介
7.3.2 离散型随机变量的方差
1. 理解取有限个值的离散型随机变量的方差及标准差的概念.
2. 能计算简单离散型随机变量的方差,并能解决一些实际问题.
活动一 背景引入
问题:从两名同学中挑出一名代表班级参加射击比赛.根据以往的成绩记录,甲、乙两名同学击中目标靶的环数X和Y的分布列分别如下表所示.
X 6 7 8 9 10
P 0.09 0.24 0.32 0.28 0.07
Y 6 7 8 9 10
P 0.07 0.22 0.38 0.30 0.03
如何评价这两名同学的射击水平?
思考
当样本均值相差不大时,可以利用样本方差考察样本数据与样本均值的偏离程度,能否用一个类似于样本方差的量来刻画离散型随机变量的波动程度呢?
活动二 随机变量的方差与标准差
1. 定义:设离散型随机变量X的分布列如下表所示.
X x1 x2 … xn
P p1 p2 … pn
则(xi-E(X))2描述了xi(i=1,2,…,n)相对于均值E(X)的偏离程度.
而D(X)=(xi-E(X))2pi为这些偏离程度的加权平均,刻画了随机变量X取值与其均值E(X)的偏离程度,我们称D(X)为随机变量X的方差,并称为随机变量X的标准差,记为σ(X).
2. 随机变量方差的意义:
随机变量的方差是一个常用来体现随机变量X取值离散程度的量,若D(X)的值越大,则表示随机变量X的取值越分散,E(X)的代表性差;若D(X)的值越小,则表示随机变量X的取值越集中,E(X)的代表性好.
3. 方差的简化计算公式:
在方差的计算中,利用下面的结论经常可以使计算简化.
D(X)=(xi-E(X))2pi
=(x-2E(X)xi+(E(X))2)pi
=xpi-2E(X)xipi+(E(X))2pi
=xpi-(E(X))2
4. 离散型随机变量的方差的性质:
D(aX+b)=a2D(X).
活动三 求离散型随机变量的方差
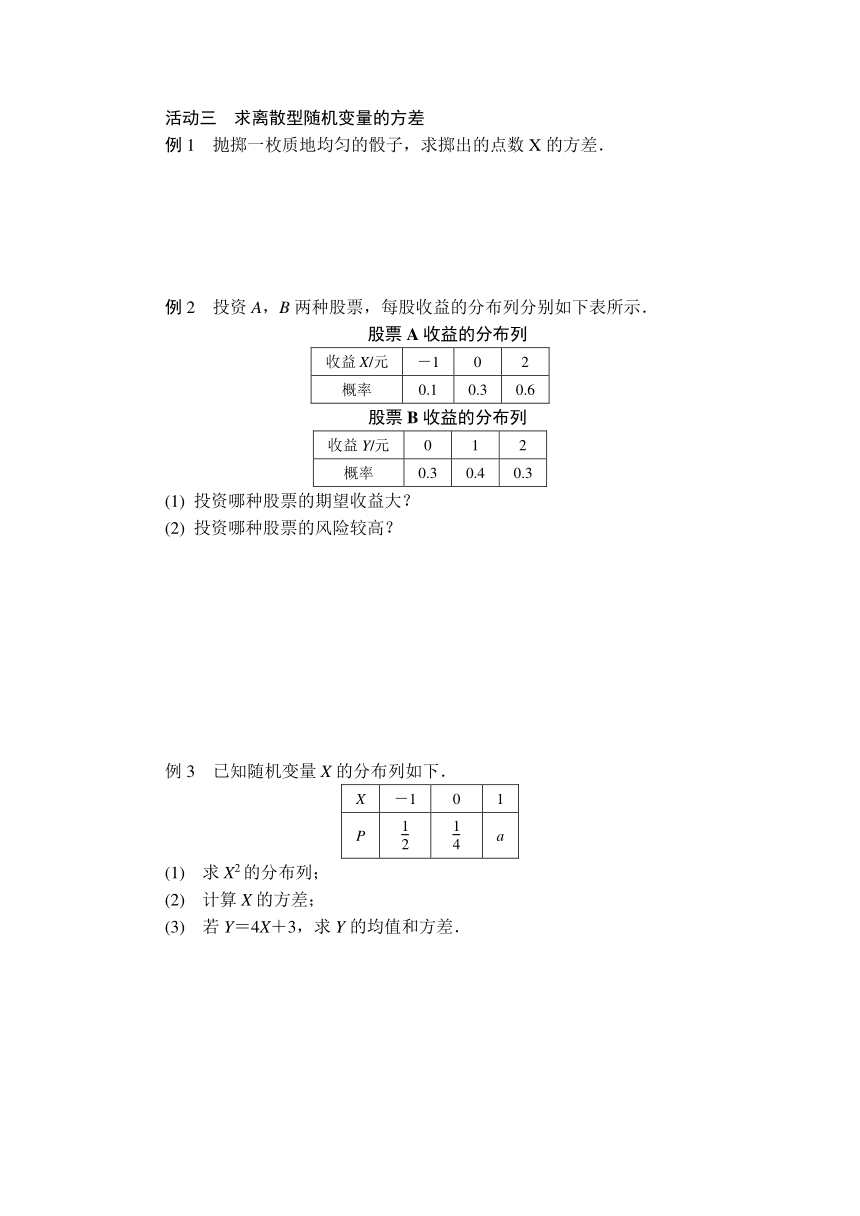
例1 抛掷一枚质地均匀的骰子,求掷出的点数X的方差.
例2 投资A,B两种股票,每股收益的分布列分别如下表所示.
股票A收益的分布列
收益X/元 -1 0 2
概率 0.1 0.3 0.6
股票B收益的分布列
收益Y/元 0 1 2
概率 0.3 0.4 0.3
(1) 投资哪种股票的期望收益大?
(2) 投资哪种股票的风险较高?
例3 已知随机变量X的分布列如下.
X -1 0 1
P a
(1) 求X2的分布列;
(2) 计算X的方差;
(3) 若Y=4X+3,求Y的均值和方差.
1. 在方差计算中,运用D(X)=xpi-(E(X))2可以使计算简化.
2. 随机变量的方差是一个重要的数字特征,它刻画了随机变量的取值与均值的偏离程度,或者说反映随机变量取值的离散程度.在不同的实际问题背景中,方差可以有不同的解释.
1. (2024南平期末)已知随机变量X的分布列如下表所示,设Y=3X-2,则D(Y)的值为( )
X -1 0 1
P n
A. 5 B. C. - D. -3
2. (2024黔西期末)设随机变量X的分布列如下(其中0X 0 1 2
P
A. 有最大值也有最小值 B. 无最大值也无最小值
C. 无最大值但有最小值 D. 有最大值但无最小值
3. (多选)设随机变量ξ的分布列为P(ξ=k)=(k=1,2,5),E(ξ),D(ξ)分别为随机变量ξ的均值与方差,则下列结论中正确的是( )
A. P(0<ξ<3.5)= B. E(3ξ+1)=7
C. D(ξ)=2 D. D(3ξ+1)=6
4. (2023辽阳期末)已知某人每次投篮的命中率为p(05. 某迷宫有三个通道,进入迷宫的每个人都要经过一扇智能门.首次到达此门,系统会随机(即等可能)为你打开一个通道,若是1号通道,则需要1 h走出迷宫;若是2号,3号通道,则分别需要2 h,3 h返回智能门.再次到达智能门时,系统会随机打开一个你未到过的通道,直至走完迷宫为止.令ξ表示走出迷宫所需的时间.求ξ的分布列、均值和方差.
7.3.2 离散型随机变量的方差
【活动方案】
问题:E(X)=6×0.09+7×0.24+8×0.32+9×0.28+10×0.07=8;E(Y)=6×0.07+7×0.22+8×0.38+9×0.30+10×0.03=8.因为两个均值相等,所以根据均值不能区分这两名同学的射击水平.
评价射击水平,除了要了解击中环数的均值外,还要考虑稳定性,即击中环数的离散程度.图1和图2分别是X和Y的概率分布图,比较两个图形,可以发现乙同学的射击成绩更集中于8环,即乙同学的射击成绩更稳定.
图1 图2
思考:能
例1 随机变量X的分布列为P(X=k)=,k=1, 2, 3, 4, 5, 6.
因为E(X)=,=×(12+22+32+42+52+62)=,
所以D(X)=-2=.
例2 (1) 股票A和股票B投资收益的期望分别为E(X)=(-1)×0.1+0×0.3+2×0.6=1.1,E(Y)=0×0.3+1×0.4+2×0.3=1.
因为E(X)>E(Y),
所以投资股票A的期望收益较大.
(2) 股票A和股票B投资收益的方差分别为D(X)=(-1)2×0.1+02×0.3+22×0.6-1.12=1.29,D(Y)=02×0.3+12×0.4+22×0.3-12=0.6.
因为E(X)和E(Y)相差不大,且D(X)>D(Y),
所以投资股票A比投资股票B的风险高.
例3 (1) 由分布列的性质,得++a=1,
解得a=,
所以X2的分布列如下表所示.
X2 0 1
P
(2) 由(1),得a=,
所以E(X)=(-1)×+0×+1×=-,
所以D(X)=×+×+×=.
(3) 因为Y=4X+3,
所以E(Y)=4E(X)+3=2,D(Y)=42D(X)=11.
【检测反馈】
1. A 由题意,得++n=1,解得n=,则E(X)=-1×+0×+1×=-,D(X)=×+×+×=.又因为Y=3X-2,所以D(Y)=9D(X)=5.
2. D 由分布列,得随机变量X的期望E(X)=0×+1×+2×=+p,则D(X)=+(p-)2+=-p2+p+=-+.由03. ABC 因为随机变量ξ的分布列为P(ξ=k)=(k=1,2,5),由分布列的性质,得P(ξ=1)+P(ξ=2)+P(ξ=5)=++=1,解得a=1,所以P(0<ξ<3.5)=P(ξ=1)+P(ξ=2)=,故A正确;因为E(ξ)=1×+2×+5×=2,所以E(3ξ+1)=3E(ξ)+1=3×2+1=7,故B正确;D(ξ)=×(1-2)2+×(2-2)2+×(5-2)2=2,故C正确;D(3ξ+1)=9D(ξ)=18,故D错误.故选ABC.
4. 2-2 由题意,得X服从两点分布,则E(X)=p,05. 由题意,得ξ的所有可能取值为1,3,4,6.
当ξ=1时,直接从1号通道走出,则P(ξ=1)=;
当ξ=3时,先走2号通道,再走1号通道,则P(ξ=3)=×=;
当ξ=4时,先走3号通道,再走1号通道,则P(ξ=4)=×=;
当ξ=6时,先走2号通道,再走3号通道,最后再走1号通道,或者先走3号通道,再走2号通道,最后走1号通道,则P(ξ=6)=2××1=,
所以随机变量ξ的分布列为
ξ 1 3 4 6
P
所以E(ξ)=1×+3×+4×+6×=,D(ξ)=2×+2×+2×+2×=.
1. 理解取有限个值的离散型随机变量的方差及标准差的概念.
2. 能计算简单离散型随机变量的方差,并能解决一些实际问题.
活动一 背景引入
问题:从两名同学中挑出一名代表班级参加射击比赛.根据以往的成绩记录,甲、乙两名同学击中目标靶的环数X和Y的分布列分别如下表所示.
X 6 7 8 9 10
P 0.09 0.24 0.32 0.28 0.07
Y 6 7 8 9 10
P 0.07 0.22 0.38 0.30 0.03
如何评价这两名同学的射击水平?
思考
当样本均值相差不大时,可以利用样本方差考察样本数据与样本均值的偏离程度,能否用一个类似于样本方差的量来刻画离散型随机变量的波动程度呢?
活动二 随机变量的方差与标准差
1. 定义:设离散型随机变量X的分布列如下表所示.
X x1 x2 … xn
P p1 p2 … pn
则(xi-E(X))2描述了xi(i=1,2,…,n)相对于均值E(X)的偏离程度.
而D(X)=(xi-E(X))2pi为这些偏离程度的加权平均,刻画了随机变量X取值与其均值E(X)的偏离程度,我们称D(X)为随机变量X的方差,并称为随机变量X的标准差,记为σ(X).
2. 随机变量方差的意义:
随机变量的方差是一个常用来体现随机变量X取值离散程度的量,若D(X)的值越大,则表示随机变量X的取值越分散,E(X)的代表性差;若D(X)的值越小,则表示随机变量X的取值越集中,E(X)的代表性好.
3. 方差的简化计算公式:
在方差的计算中,利用下面的结论经常可以使计算简化.
D(X)=(xi-E(X))2pi
=(x-2E(X)xi+(E(X))2)pi
=xpi-2E(X)xipi+(E(X))2pi
=xpi-(E(X))2
4. 离散型随机变量的方差的性质:
D(aX+b)=a2D(X).
活动三 求离散型随机变量的方差
例1 抛掷一枚质地均匀的骰子,求掷出的点数X的方差.
例2 投资A,B两种股票,每股收益的分布列分别如下表所示.
股票A收益的分布列
收益X/元 -1 0 2
概率 0.1 0.3 0.6
股票B收益的分布列
收益Y/元 0 1 2
概率 0.3 0.4 0.3
(1) 投资哪种股票的期望收益大?
(2) 投资哪种股票的风险较高?
例3 已知随机变量X的分布列如下.
X -1 0 1
P a
(1) 求X2的分布列;
(2) 计算X的方差;
(3) 若Y=4X+3,求Y的均值和方差.
1. 在方差计算中,运用D(X)=xpi-(E(X))2可以使计算简化.
2. 随机变量的方差是一个重要的数字特征,它刻画了随机变量的取值与均值的偏离程度,或者说反映随机变量取值的离散程度.在不同的实际问题背景中,方差可以有不同的解释.
1. (2024南平期末)已知随机变量X的分布列如下表所示,设Y=3X-2,则D(Y)的值为( )
X -1 0 1
P n
A. 5 B. C. - D. -3
2. (2024黔西期末)设随机变量X的分布列如下(其中0
P
A. 有最大值也有最小值 B. 无最大值也无最小值
C. 无最大值但有最小值 D. 有最大值但无最小值
3. (多选)设随机变量ξ的分布列为P(ξ=k)=(k=1,2,5),E(ξ),D(ξ)分别为随机变量ξ的均值与方差,则下列结论中正确的是( )
A. P(0<ξ<3.5)= B. E(3ξ+1)=7
C. D(ξ)=2 D. D(3ξ+1)=6
4. (2023辽阳期末)已知某人每次投篮的命中率为p(0
7.3.2 离散型随机变量的方差
【活动方案】
问题:E(X)=6×0.09+7×0.24+8×0.32+9×0.28+10×0.07=8;E(Y)=6×0.07+7×0.22+8×0.38+9×0.30+10×0.03=8.因为两个均值相等,所以根据均值不能区分这两名同学的射击水平.
评价射击水平,除了要了解击中环数的均值外,还要考虑稳定性,即击中环数的离散程度.图1和图2分别是X和Y的概率分布图,比较两个图形,可以发现乙同学的射击成绩更集中于8环,即乙同学的射击成绩更稳定.
图1 图2
思考:能
例1 随机变量X的分布列为P(X=k)=,k=1, 2, 3, 4, 5, 6.
因为E(X)=,=×(12+22+32+42+52+62)=,
所以D(X)=-2=.
例2 (1) 股票A和股票B投资收益的期望分别为E(X)=(-1)×0.1+0×0.3+2×0.6=1.1,E(Y)=0×0.3+1×0.4+2×0.3=1.
因为E(X)>E(Y),
所以投资股票A的期望收益较大.
(2) 股票A和股票B投资收益的方差分别为D(X)=(-1)2×0.1+02×0.3+22×0.6-1.12=1.29,D(Y)=02×0.3+12×0.4+22×0.3-12=0.6.
因为E(X)和E(Y)相差不大,且D(X)>D(Y),
所以投资股票A比投资股票B的风险高.
例3 (1) 由分布列的性质,得++a=1,
解得a=,
所以X2的分布列如下表所示.
X2 0 1
P
(2) 由(1),得a=,
所以E(X)=(-1)×+0×+1×=-,
所以D(X)=×+×+×=.
(3) 因为Y=4X+3,
所以E(Y)=4E(X)+3=2,D(Y)=42D(X)=11.
【检测反馈】
1. A 由题意,得++n=1,解得n=,则E(X)=-1×+0×+1×=-,D(X)=×+×+×=.又因为Y=3X-2,所以D(Y)=9D(X)=5.
2. D 由分布列,得随机变量X的期望E(X)=0×+1×+2×=+p,则D(X)=+(p-)2+=-p2+p+=-+.由0
4. 2-2 由题意,得X服从两点分布,则E(X)=p,0
当ξ=1时,直接从1号通道走出,则P(ξ=1)=;
当ξ=3时,先走2号通道,再走1号通道,则P(ξ=3)=×=;
当ξ=4时,先走3号通道,再走1号通道,则P(ξ=4)=×=;
当ξ=6时,先走2号通道,再走3号通道,最后再走1号通道,或者先走3号通道,再走2号通道,最后走1号通道,则P(ξ=6)=2××1=,
所以随机变量ξ的分布列为
ξ 1 3 4 6
P
所以E(ξ)=1×+3×+4×+6×=,D(ξ)=2×+2×+2×+2×=.
