8.1.2 样本相关系数 同步学案(含答案) 2024~2025学年高二数学人教A版(2019)选择性必修3
文档属性
| 名称 | 8.1.2 样本相关系数 同步学案(含答案) 2024~2025学年高二数学人教A版(2019)选择性必修3 |  | |
| 格式 | docx | ||
| 文件大小 | 248.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-26 23:54:35 | ||
图片预览

文档简介
8.1.2 样本相关系数
1. 结合实例,了解样本相关系数的统计含义,同时要了解它与标准化数据向量夹角的关系.
2. 结合实例,会通过相关系数比较多组成对数据的相关性.
活动一 样本相关系数
由给出的成对样本数据,可以画出其变量间的散点图,通过观察,可以大致推断两个变量是否存在相关关系、是正相关还是负相关、是线性相关还是非线性相关等,但无法确切地知道成对数据的相关程度,更无法量化其相关程度的大小.
思考
类比统计中的数字特征,用哪个恰当的“数字特征”来刻画成对样本数据的相关程度?
1. 样本相关系数r的计算公式
我们可以利用相关系数来定量地衡量两个变量之间的线性相关关系,计算公式为
r=.
2. 样本相关系数r的性质
①|r|≤1;
②当r>0时,称成对样本数据正相关;当r<0时,称成对样本数据负相关;
③当|r|越接近1时,成对样本数据的线性相关程度越强;
④当|r|越接近0时,成对样本数据的线性相关程度越弱.
活动二 成对数据的相关程度
例1 根据教材的表8.11中脂肪含量和年龄的样本数据,推断两个变量是否线性相关,计算样本相关系数,并推断它们的相关程度.
通过抽样获取两个变量的一些成对数据,再计算样本相关系数,通过样本相关系数去估计总体相关系数,从而了解两个变量之间的相关程度.
20个工业企业某年的平均固定资产价值与总价值(单位:百万元)如下表所示.
企业编号 1 2 3 4 5 6 7 8 9 10
年平均固定资产价值 36 43 50 40 55 58 38 45 47 42
年总产值 32.0 40.2 47.5 41.5 51.0 53.4 33.8 42.8 45.6 40.8
企业编号 11 12 13 14 15 16 17 18 19 20
年平均固定资产价值 50 70 62 58 52 63 64 53 54 56
年总产值 45.5 65.0 56.0 55.0 55.0 57.0 54.2 56.5 50.2 49.2
设年平均固定资产价值为x,年总产值为y,单位均为百万元.试画出散点图,计算相关系数.
例2 在某校高一年级中随机抽取25名男生,测得他们的身高、体重、臂展等数据,如下表所示.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13
身高/cm 173 179 175 179 182 173 180 170 169 177 177 178 174
体重/kg 55 71 52 62 82 63 55 81 54 54 59 67 56
臂展/cm 169 170 172 177 174 166 174 169 166 176 170 174 170
编号 14 15 16 17 18 19 20 21 22 23 24 25
身高/cm 166 176 176 175 169 184 169 182 171 177 173 173
体重/kg 66 61 49 60 48 86 58 54 58 61 58 51
臂展/cm 161 166 165 173 162 189 164 170 164 173 165 169
体重与身高、臂展与身高分别具有怎样的相关性?
对两个变量x,y进行线性相关检验,得线性相关系数r1=0.785 9,对两个变量u,v进行线性相关检验,得线性相关系数r2=-0.956 8,则下列判断中正确的是( )
A. 变量x与y正相关,变量u与v负相关,变量x与y的线性相关性较强
B. 变量x与y负相关,变量u与v正相关,变量x与y的线性相关性较强
C. 变量x与y正相关,变量u与v负相关,变量u与v的线性相关性较强
D. 变量x与y负相关,变量u与v正相关,变量u与v的线性相关性较强
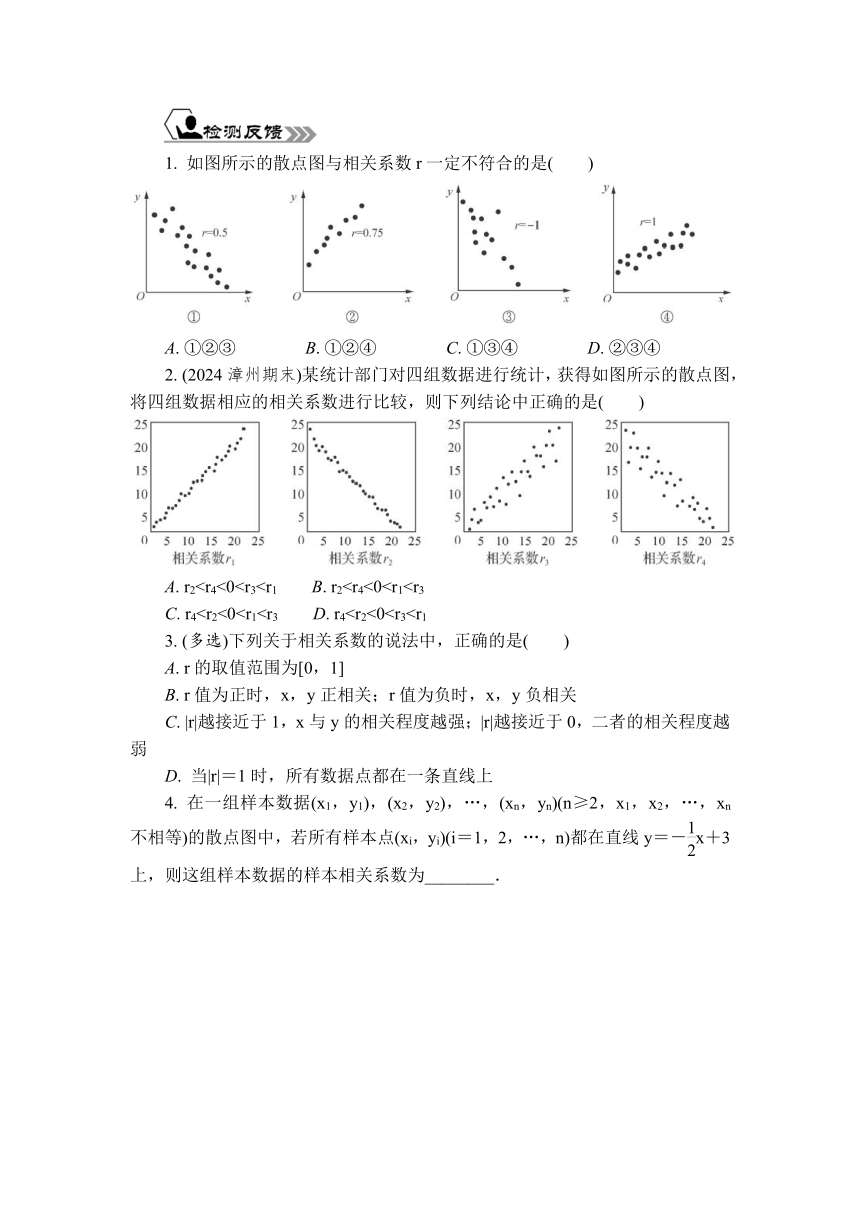
1. 如图所示的散点图与相关系数r一定不符合的是( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④
2. (2024漳州期末)某统计部门对四组数据进行统计,获得如图所示的散点图,将四组数据相应的相关系数进行比较,则下列结论中正确的是( )
A. r2C. r43. (多选)下列关于相关系数的说法中,正确的是( )
A. r的取值范围为[0,1]
B. r值为正时,x,y正相关;r值为负时,x,y负相关
C. |r|越接近于1,x与y的相关程度越强;|r|越接近于0,二者的相关程度越弱
D. 当|r|=1时,所有数据点都在一条直线上
4. 在一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不相等)的散点图中,若所有样本点(xi,yi)(i=1,2,…,n)都在直线y=-x+3上,则这组样本数据的样本相关系数为________.
5. (2024哈尔滨期末)某校高一新生共1 000人,男女比例为1∶1,经统计,身高大于170cm的学生共600人,其中女生200人.该校为了解高一新生身高和体重的关系,在新生中随机抽测了10人的身高(单位:cm)和体重(单位:kg)作为一个样本,所得样本数据如下表所示:
编号 1 2 3 4 5 6 7 8 9 10
身高x/cm 164 165 170 172 173 174 176 177 179 180
体重y/kg 57 58 65 65 90 70 75 76 80 84
(1) 在对这10个学生组成的样本的检测过程中,采用不放回的方式,每次随机抽取1人检测.
①若已进行了三次抽取,求抽取的这三人中至少有两人体重大于74kg的概率;
②求第一次抽取的学生体重大于79kg且第二次抽取的学生身高大于175cm的概率;
(2) 由表中数据的散点图分析,编号为5的数据构成的点(173,90)为离群点.所以应去掉该数据后再求经验回归方程.已知未去掉离群点的样本相关系数约为0.802,请用样本相关系数说明去掉离群点(173,90)的合理性(相关系数r保留三位小数).
参考公式及数据:样本相关系数r==,=1 730,=720,=124 990,=266,×≈437.6.
8.1.2 样本相关系数
【活动方案】
思考:略
例1 先画出散点图(图略),观察散点图,可以看出样本点都集中在一条直线附近,由此推断脂肪含量和年龄线性相关.
根据样本相关系数的定义,
r=
=.①
利用计算工具计算可得
≈48.07,≈27.26,=19 403.2,
=34 181,=11 051.77.
代入①式,得
r≈≈0.97.
由样本相关系数r≈0.97,可以推断脂肪含量和年龄这两个变量正线性相关,且相关程度很强.
跟踪训练 散点图如图所示.
由表中数据可得=1 036,=972.2,=51 752.3,=55 314,=48 590.2.
根据r=
=,
可得相关系数为r≈0.939 6.
因此,y与x有着很强的正相关关系.
例2 根据样本数据画出体重与身高、臂展与身高的散点图,分别如图1和图2所示,两个散点图都呈现出线性相关的特征.
通过计算得到体重与身高、臂展与身高的样本相关系数分别约为0.34和0.78,都为正线性相关.其中,臂展与身高的相关程度更高.
跟踪训练 C 由线性相关系数r1=0.785 9>0,知x与y正相关,由线性相关系数r2=-0.956 8<0,知u与v负相关,故B,D错误;又|r1|<|r2|,所以变量u与v的线性相关性比x与y的线性相关性强,故A错误,C正确.
【检测反馈】
1. C ①中,由散点图可得,两相关变量负相关,故①错误;②中,由散点图可得,两相关变量正相关,且相关系数可能是r=0.75;③中,若相关系数r=-1,则所有点应该分布在一条直线上,散点图显然不符合,故③错误;④中,若相关系数r=1,则所有的点应该分布在一条直线上,散点图显然不符合,故④错误.综上,①③④一定不符合.
2. A 由图可知,从左到右第一幅图、第三幅图是正相关,第二幅图、第四幅图是负相关,且第一幅图、第二幅图的点相对更加集中,所以r1更加接近1,r2更加接近-1,所以r23. BCD 由相关系数的含义知,r的取值范围为[-1,1],故A错误;B,C,D显然正确.故选BCD.
4. -1 因为-<0,且所有样本点(xi,yi)(i=1,2,…,n)都在直线y=-x+3上,所以这组样本数据的样本相关系数为-1.
5. (1) ①记抽取的这三人中至少有两人体重大于74kg为事件M,
则P(M)=+=,
即抽取的这三人中至少有两人体重大于74kg的概率为.
②记第一次抽取的学生体重大于79kg为事件A,第二次抽取的学生身高大于175cm为事件B.
因为样本中学生身高大于175cm的有4人,身高大于175cm且体重大于79kg的有2人,身高小于175cm且体重大于79kg的有1人,
所以P(AB)=×+×=,
即第一次抽取的学生体重大于79kg且第二次的抽取的学生身高大于175cm的概率为.
(2) 设未去离群点的样本相关系数为r1,去掉离群点后的样本相关系数为r2,则r1≈0.802.
去掉离群点后,=-173=1 730-173=1 557,==173,
=-90=720-90=630,==70,
=-173×90=124 990-15 570=109 420,
==266,
=(-13)2+(-12)2+(-5)2+(-5)2+52+62+102+142=720,
又=-n,
所以r2==≈≈0.983.
因为r2>r1>0,且r2相比r1更接近1,
所以去掉离群点后的y与x的线性相关性更强,所以去掉离群点(173,90)是合理的.
1. 结合实例,了解样本相关系数的统计含义,同时要了解它与标准化数据向量夹角的关系.
2. 结合实例,会通过相关系数比较多组成对数据的相关性.
活动一 样本相关系数
由给出的成对样本数据,可以画出其变量间的散点图,通过观察,可以大致推断两个变量是否存在相关关系、是正相关还是负相关、是线性相关还是非线性相关等,但无法确切地知道成对数据的相关程度,更无法量化其相关程度的大小.
思考
类比统计中的数字特征,用哪个恰当的“数字特征”来刻画成对样本数据的相关程度?
1. 样本相关系数r的计算公式
我们可以利用相关系数来定量地衡量两个变量之间的线性相关关系,计算公式为
r=.
2. 样本相关系数r的性质
①|r|≤1;
②当r>0时,称成对样本数据正相关;当r<0时,称成对样本数据负相关;
③当|r|越接近1时,成对样本数据的线性相关程度越强;
④当|r|越接近0时,成对样本数据的线性相关程度越弱.
活动二 成对数据的相关程度
例1 根据教材的表8.11中脂肪含量和年龄的样本数据,推断两个变量是否线性相关,计算样本相关系数,并推断它们的相关程度.
通过抽样获取两个变量的一些成对数据,再计算样本相关系数,通过样本相关系数去估计总体相关系数,从而了解两个变量之间的相关程度.
20个工业企业某年的平均固定资产价值与总价值(单位:百万元)如下表所示.
企业编号 1 2 3 4 5 6 7 8 9 10
年平均固定资产价值 36 43 50 40 55 58 38 45 47 42
年总产值 32.0 40.2 47.5 41.5 51.0 53.4 33.8 42.8 45.6 40.8
企业编号 11 12 13 14 15 16 17 18 19 20
年平均固定资产价值 50 70 62 58 52 63 64 53 54 56
年总产值 45.5 65.0 56.0 55.0 55.0 57.0 54.2 56.5 50.2 49.2
设年平均固定资产价值为x,年总产值为y,单位均为百万元.试画出散点图,计算相关系数.
例2 在某校高一年级中随机抽取25名男生,测得他们的身高、体重、臂展等数据,如下表所示.
编号 1 2 3 4 5 6 7 8 9 10 11 12 13
身高/cm 173 179 175 179 182 173 180 170 169 177 177 178 174
体重/kg 55 71 52 62 82 63 55 81 54 54 59 67 56
臂展/cm 169 170 172 177 174 166 174 169 166 176 170 174 170
编号 14 15 16 17 18 19 20 21 22 23 24 25
身高/cm 166 176 176 175 169 184 169 182 171 177 173 173
体重/kg 66 61 49 60 48 86 58 54 58 61 58 51
臂展/cm 161 166 165 173 162 189 164 170 164 173 165 169
体重与身高、臂展与身高分别具有怎样的相关性?
对两个变量x,y进行线性相关检验,得线性相关系数r1=0.785 9,对两个变量u,v进行线性相关检验,得线性相关系数r2=-0.956 8,则下列判断中正确的是( )
A. 变量x与y正相关,变量u与v负相关,变量x与y的线性相关性较强
B. 变量x与y负相关,变量u与v正相关,变量x与y的线性相关性较强
C. 变量x与y正相关,变量u与v负相关,变量u与v的线性相关性较强
D. 变量x与y负相关,变量u与v正相关,变量u与v的线性相关性较强
1. 如图所示的散点图与相关系数r一定不符合的是( )
A. ①②③ B. ①②④ C. ①③④ D. ②③④
2. (2024漳州期末)某统计部门对四组数据进行统计,获得如图所示的散点图,将四组数据相应的相关系数进行比较,则下列结论中正确的是( )
A. r2
A. r的取值范围为[0,1]
B. r值为正时,x,y正相关;r值为负时,x,y负相关
C. |r|越接近于1,x与y的相关程度越强;|r|越接近于0,二者的相关程度越弱
D. 当|r|=1时,所有数据点都在一条直线上
4. 在一组样本数据(x1,y1),(x2,y2),…,(xn,yn)(n≥2,x1,x2,…,xn不相等)的散点图中,若所有样本点(xi,yi)(i=1,2,…,n)都在直线y=-x+3上,则这组样本数据的样本相关系数为________.
5. (2024哈尔滨期末)某校高一新生共1 000人,男女比例为1∶1,经统计,身高大于170cm的学生共600人,其中女生200人.该校为了解高一新生身高和体重的关系,在新生中随机抽测了10人的身高(单位:cm)和体重(单位:kg)作为一个样本,所得样本数据如下表所示:
编号 1 2 3 4 5 6 7 8 9 10
身高x/cm 164 165 170 172 173 174 176 177 179 180
体重y/kg 57 58 65 65 90 70 75 76 80 84
(1) 在对这10个学生组成的样本的检测过程中,采用不放回的方式,每次随机抽取1人检测.
①若已进行了三次抽取,求抽取的这三人中至少有两人体重大于74kg的概率;
②求第一次抽取的学生体重大于79kg且第二次抽取的学生身高大于175cm的概率;
(2) 由表中数据的散点图分析,编号为5的数据构成的点(173,90)为离群点.所以应去掉该数据后再求经验回归方程.已知未去掉离群点的样本相关系数约为0.802,请用样本相关系数说明去掉离群点(173,90)的合理性(相关系数r保留三位小数).
参考公式及数据:样本相关系数r==,=1 730,=720,=124 990,=266,×≈437.6.
8.1.2 样本相关系数
【活动方案】
思考:略
例1 先画出散点图(图略),观察散点图,可以看出样本点都集中在一条直线附近,由此推断脂肪含量和年龄线性相关.
根据样本相关系数的定义,
r=
=.①
利用计算工具计算可得
≈48.07,≈27.26,=19 403.2,
=34 181,=11 051.77.
代入①式,得
r≈≈0.97.
由样本相关系数r≈0.97,可以推断脂肪含量和年龄这两个变量正线性相关,且相关程度很强.
跟踪训练 散点图如图所示.
由表中数据可得=1 036,=972.2,=51 752.3,=55 314,=48 590.2.
根据r=
=,
可得相关系数为r≈0.939 6.
因此,y与x有着很强的正相关关系.
例2 根据样本数据画出体重与身高、臂展与身高的散点图,分别如图1和图2所示,两个散点图都呈现出线性相关的特征.
通过计算得到体重与身高、臂展与身高的样本相关系数分别约为0.34和0.78,都为正线性相关.其中,臂展与身高的相关程度更高.
跟踪训练 C 由线性相关系数r1=0.785 9>0,知x与y正相关,由线性相关系数r2=-0.956 8<0,知u与v负相关,故B,D错误;又|r1|<|r2|,所以变量u与v的线性相关性比x与y的线性相关性强,故A错误,C正确.
【检测反馈】
1. C ①中,由散点图可得,两相关变量负相关,故①错误;②中,由散点图可得,两相关变量正相关,且相关系数可能是r=0.75;③中,若相关系数r=-1,则所有点应该分布在一条直线上,散点图显然不符合,故③错误;④中,若相关系数r=1,则所有的点应该分布在一条直线上,散点图显然不符合,故④错误.综上,①③④一定不符合.
2. A 由图可知,从左到右第一幅图、第三幅图是正相关,第二幅图、第四幅图是负相关,且第一幅图、第二幅图的点相对更加集中,所以r1更加接近1,r2更加接近-1,所以r2
4. -1 因为-<0,且所有样本点(xi,yi)(i=1,2,…,n)都在直线y=-x+3上,所以这组样本数据的样本相关系数为-1.
5. (1) ①记抽取的这三人中至少有两人体重大于74kg为事件M,
则P(M)=+=,
即抽取的这三人中至少有两人体重大于74kg的概率为.
②记第一次抽取的学生体重大于79kg为事件A,第二次抽取的学生身高大于175cm为事件B.
因为样本中学生身高大于175cm的有4人,身高大于175cm且体重大于79kg的有2人,身高小于175cm且体重大于79kg的有1人,
所以P(AB)=×+×=,
即第一次抽取的学生体重大于79kg且第二次的抽取的学生身高大于175cm的概率为.
(2) 设未去离群点的样本相关系数为r1,去掉离群点后的样本相关系数为r2,则r1≈0.802.
去掉离群点后,=-173=1 730-173=1 557,==173,
=-90=720-90=630,==70,
=-173×90=124 990-15 570=109 420,
==266,
=(-13)2+(-12)2+(-5)2+(-5)2+52+62+102+142=720,
又=-n,
所以r2==≈≈0.983.
因为r2>r1>0,且r2相比r1更接近1,
所以去掉离群点后的y与x的线性相关性更强,所以去掉离群点(173,90)是合理的.
