第八章成对数据的统计分析 复习学案(含答案)2024~2025学年高二数学人教A版(2019)选择性必修3
文档属性
| 名称 | 第八章成对数据的统计分析 复习学案(含答案)2024~2025学年高二数学人教A版(2019)选择性必修3 | 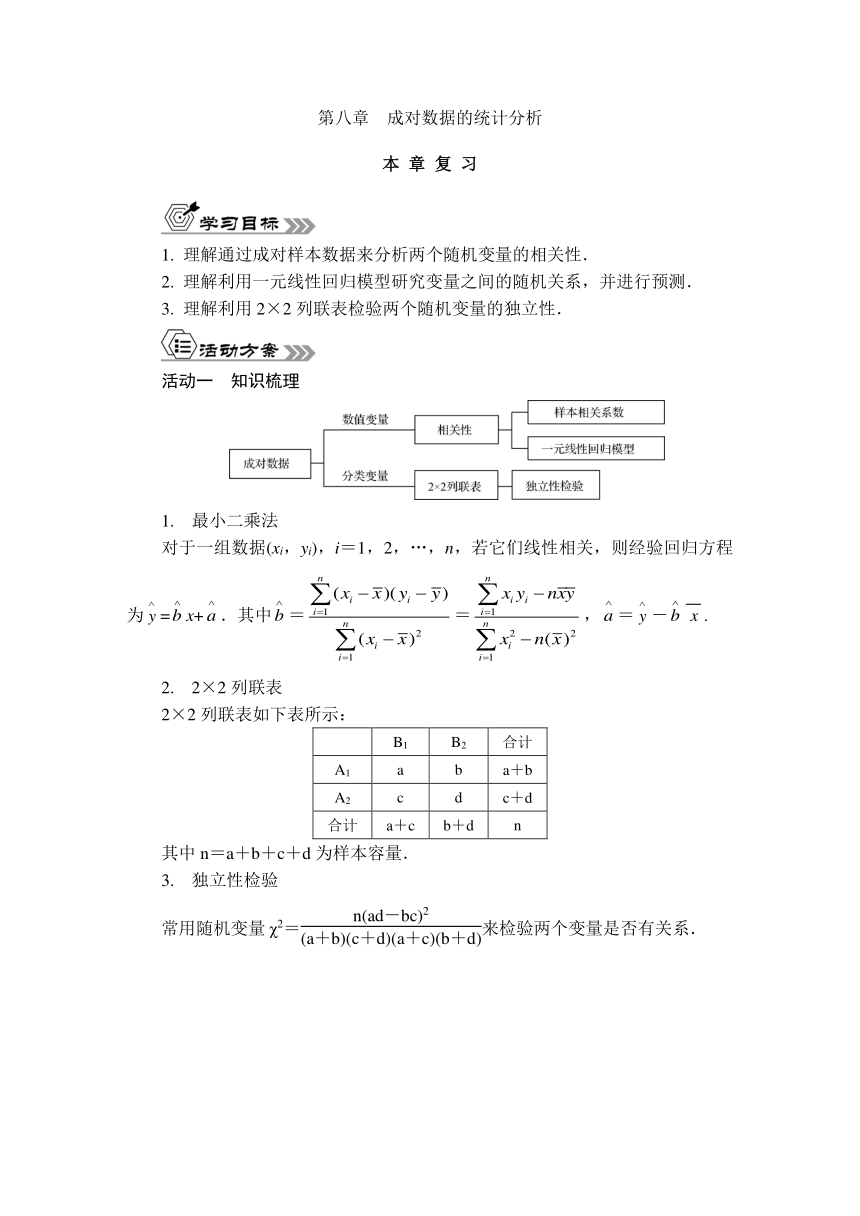 | |
| 格式 | docx | ||
| 文件大小 | 156.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-26 23:58:24 | ||
图片预览



文档简介
第八章 成对数据的统计分析
本 章 复 习
1. 理解通过成对样本数据来分析两个随机变量的相关性.
2. 理解利用一元线性回归模型研究变量之间的随机关系,并进行预测.
3. 理解利用2×2列联表检验两个随机变量的独立性.
活动一 知识梳理
1. 最小二乘法
对于一组数据(xi,yi),i=1,2,…,n,若它们线性相关,则经验回归方程为=x+.其中==,=-.
2. 2×2列联表
2×2列联表如下表所示:
B1 B2 合计
A1 a b a+b
A2 c d c+d
合计 a+c b+d n
其中n=a+b+c+d为样本容量.
3. 独立性检验
常用随机变量χ2=来检验两个变量是否有关系.
活动二 回归分析
例1 (2024广东期中)某地政府为提高当地农民收入,指导农民种植药材,取得较好的效果.以下是某农户近5年种植药材的年收入的统计数据:
年份 2019 2020 2021 2022 2023
年份代码x 1 2 3 4 5
年收入y/千元 59 61 64 68 73
(1) 根据表中的数据,现决定使用函数模型y=bx2+a来拟合y与x之间的关系,请求出此模型的经验回归方程(结果保留一位小数);
(2) 统计学中常通过计算残差的平方和来判断模型的拟合效果.在本题中,若残差平方和小于0.5,则认为拟合效果符合要求.请判断(1)中经验回归方程的拟合效果是否符合要求,并说明理由.
活动三 独立性检验
例2 研究人员选取170名青年男女大学生的样本,对他们进行一种心理测验,发现有60名女生对该心理测验中的最后一个题目的反应是:作肯定的有22名,否定的有38名;110名男生在相同的项目上作肯定的有22名,否定的有88名.问:性别与态度之间是否存在某种关系?分别用等高过高堆积条形图和独立性检验的方法判断.
1. (2024天津)下列图中,样本相关系数最大的是( )
2. (2024山东实验中学月考)为研究某池塘中水生植物的覆盖水塘面积x(单位:dm2)与水生植物的株数y(单位:株)之间的相关关系,收集了4组数据,用模型y=cekx(c>0)去拟合x与y的关系,设z=ln y,x与z的数据如下表格所示,得到x与z的经验回归方程为=1.2x+,则实数c的值为( )
x 3 4 6 7
z 2 2.5 4.5 7
A. -2 B. -1 C. e-2 D. e-1
3. (多选)(2024临沂一模)下列命题中,正确的是( )
A. 一组样本数据的散点图中,若所有样本点(xi,yi)都在直线y=0.95x+1上,则这组样本数据的样本相关系数为0.95
B. 已知随机变量ξ~N(3,4),若ξ=2η+1,则D(η)=1
C. 在2×2列联表中,若每个数据a,b,c,d均变成原来的2倍,则χ2也变成原来的2倍(χ2=,其中n=a+b+c+d)
D. 分别抛掷2枚质地均匀的骰子,若事件A=“第一枚骰子正面向上的点数是奇数”,B=“2枚骰子正面向上的点数相同”,则A,B互为独立事件
4. 某商场为一种商品进行合理定价,将该商品按事先拟定的价格进行试销,得到如下数据:
单价x/元 8 8.2 8.4 8.6 8.8 9
销量y/件 90 84 83 80 75 68
(1) 按照上述数据,则y关于x的经验回归方程为______________;
(2) 预计在今后的销售中,销量与单价仍然满足(1)中的关系,若该商品的成本是每件7.5元,为使商场获得最大利润,该商品的单价应定为________元.(利润=销售收入-成本)
5. (2024全国甲卷)某工厂进行生产线智能化升级改造,升级改造后,从该工厂甲、乙两个车间的产品中随机抽取150件进行检验,数据如下:
优级品 合格品 不合格品 合计
甲车间 26 24 0 50
乙车间 70 28 2 100
合计 96 52 2 150
(1) 填写如下列联表:
优级品 非优级品
甲车间
乙车间
能否有95%的把握认为甲、乙两车间产品的优级品率存在差异?能否有99%的把握认为甲,乙两车间产品的优级品率存在差异?
(2) 已知升级改造前该工厂产品的优级品率p=0.5,设为升级改造后抽取的n件产品的优级品率.如果 >p+1.65,则认为该工厂产品的优级品率提高了,根据抽取的150件产品的数据,能否认为生产线智能化升级改造后,该工厂产品的优级品率提高了?(参考数据:≈12.247)
附:χ2=,其中n=a+b+c+d.
α 0.050 0.010 0.001
xα 3.841 6.635 10.828
第八章 成对数据的统计分析
本 章 复 习
【活动方案】
例1 (1) 根据农户近5年种植药材的收入情况的统计数据可得=(1+2+3+4+5)=3,=(59+61+64+68+73)=65,
设t=x2,则y=bx2+a=bt+a,
所以=(12+22+32+42+52)=11,
则b==≈0.6,
a=-b=65-×11≈58.6.
故所求经验回归方程为y=0.6x2+58.6.
(2) 将x值代入可得估计值分别为59.2,61,64,68.2,73.6,
则残差平方和为(59-59.2)2+(61-61)2+(64-64)2+(68-68.2)2+(73-73.6)2=0.44.
因为0.44<0.5,
所以经验回归方程y=0.6x2+58.6拟合效果符合要求.
例2 建立性别与态度的2×2列联表如下:
肯定 否定 合计
男生 22 88 110
女生 22 38 60
合计 44 126 170
根据列联表中所给的数据,可求出男生中作肯定态度的频率为=0.2,女生中作肯定态度的频率为≈0.37.作等高堆积条形图如图,其中两个深色条形的高分别表示男生和女生中作肯定态度的频率,比较图中深色条形的高可以发现,女生中作肯定态度的频率明显高于男生中作肯定态度的频率,因此可以认为性别与态度有关系.
零假设为H0:性别和态度没有关系.
根据列联表中的数据得到
χ2=≈5.622>3.841=x0.05.
根据小概率值α=0.05的χ2独立性检验,我们推断H0不成立,即认为性别和态度有关系,此推断犯错误的概率不大于0.05.
【检测反馈】
1. A 观察选项可知,A中散点分布比较集中,且集合在某一条直线的附近,线性回归模型拟合效果比较好,呈现明显的正相关,故A中的样本相关系数最大.
2. C 因为==5,==4,所以4=1.2×5+,解得=-2,所以=1.2x-2.由z=ln y,得ln y=1.2x-2,所以,y=e1.2x-2=e-2·e1.2x,则c=e-2.
3. BCD 对于A,若所有样本点(xi,yi)都在直线y=0.95x+1上,则这组样本数据的样本相关系数为1,故A错误;对于B,由ξ~N(3,4),得D(ξ)=4.又ξ=2η+1,即η=ξ-,则D(η)=×D(ξ)=1,故B正确;对于C,在2×2列联表中,若每个数据a,b,c,d均变成原来的2倍,则χ2==,即χ2也变成原来的2倍,故C正确;对于D,分别抛掷2枚质地均匀的骰子,基本事件总数为6×6=36,事件A=“第一枚骰子正面向上的点数是奇数”,则事件A包含的基本事件数为3×6=18,事件B=“2枚骰子正面向上的点数相同”,则事件B包含的基本事件数为6×1=6,所以P(A)==,P(B)==.又事件AB包含的基本事件数为3×1=3,所以P(AB)==,所以P(AB)=P(A)×P(B),则A,B互为独立事件,故D正确.故选BCD.
4. (1)=-20x+250 设经验回归方程为=x+,由题意知,=×(8+8.2+8.4+8.6+8.8+9)=8.5,=×(90+84+83+80+75+68)=80,=-14,=0.7,所以==-20,=-=80+20×8.5=250,所以经验回归方程为=-20x+250.
(2) 10 设商场获得的利润为W元,由题意,得W=x(-20x+250)-7.5(-20x+250)=-20x2+400x-1 875=-20(x-10)2+125,当且仅当x=10时,W取得最大值,故当单价定为10元时,商场可获得最大利润.
5. (1) 根据题意可得列联表如下:
优级品 非优级品
甲车间 26 24
乙车间 70 30
可得χ2===4.687 5,
因为3.841<4.687 5<6.635,
所以有95%的把握认为甲、乙两车间产品的优级品率存在差异,没有99%的把握认为甲,乙两车间产品的优级品率存在差异.
(2) 由题意可知生产线智能化升级改造后,该工厂产品的优级品的频率为=0.64,
用频率估计概率可得=0.64,
又因为升级改造前该工厂产品的优级品率p=0.5,
所以p+1.65=0.5+1.65≈0.5+1.65×≈0.567,
可知>p+1.65,
所以可以认为生产线智能化升级改造后,该工厂产品的优级品率提高了.
本 章 复 习
1. 理解通过成对样本数据来分析两个随机变量的相关性.
2. 理解利用一元线性回归模型研究变量之间的随机关系,并进行预测.
3. 理解利用2×2列联表检验两个随机变量的独立性.
活动一 知识梳理
1. 最小二乘法
对于一组数据(xi,yi),i=1,2,…,n,若它们线性相关,则经验回归方程为=x+.其中==,=-.
2. 2×2列联表
2×2列联表如下表所示:
B1 B2 合计
A1 a b a+b
A2 c d c+d
合计 a+c b+d n
其中n=a+b+c+d为样本容量.
3. 独立性检验
常用随机变量χ2=来检验两个变量是否有关系.
活动二 回归分析
例1 (2024广东期中)某地政府为提高当地农民收入,指导农民种植药材,取得较好的效果.以下是某农户近5年种植药材的年收入的统计数据:
年份 2019 2020 2021 2022 2023
年份代码x 1 2 3 4 5
年收入y/千元 59 61 64 68 73
(1) 根据表中的数据,现决定使用函数模型y=bx2+a来拟合y与x之间的关系,请求出此模型的经验回归方程(结果保留一位小数);
(2) 统计学中常通过计算残差的平方和来判断模型的拟合效果.在本题中,若残差平方和小于0.5,则认为拟合效果符合要求.请判断(1)中经验回归方程的拟合效果是否符合要求,并说明理由.
活动三 独立性检验
例2 研究人员选取170名青年男女大学生的样本,对他们进行一种心理测验,发现有60名女生对该心理测验中的最后一个题目的反应是:作肯定的有22名,否定的有38名;110名男生在相同的项目上作肯定的有22名,否定的有88名.问:性别与态度之间是否存在某种关系?分别用等高过高堆积条形图和独立性检验的方法判断.
1. (2024天津)下列图中,样本相关系数最大的是( )
2. (2024山东实验中学月考)为研究某池塘中水生植物的覆盖水塘面积x(单位:dm2)与水生植物的株数y(单位:株)之间的相关关系,收集了4组数据,用模型y=cekx(c>0)去拟合x与y的关系,设z=ln y,x与z的数据如下表格所示,得到x与z的经验回归方程为=1.2x+,则实数c的值为( )
x 3 4 6 7
z 2 2.5 4.5 7
A. -2 B. -1 C. e-2 D. e-1
3. (多选)(2024临沂一模)下列命题中,正确的是( )
A. 一组样本数据的散点图中,若所有样本点(xi,yi)都在直线y=0.95x+1上,则这组样本数据的样本相关系数为0.95
B. 已知随机变量ξ~N(3,4),若ξ=2η+1,则D(η)=1
C. 在2×2列联表中,若每个数据a,b,c,d均变成原来的2倍,则χ2也变成原来的2倍(χ2=,其中n=a+b+c+d)
D. 分别抛掷2枚质地均匀的骰子,若事件A=“第一枚骰子正面向上的点数是奇数”,B=“2枚骰子正面向上的点数相同”,则A,B互为独立事件
4. 某商场为一种商品进行合理定价,将该商品按事先拟定的价格进行试销,得到如下数据:
单价x/元 8 8.2 8.4 8.6 8.8 9
销量y/件 90 84 83 80 75 68
(1) 按照上述数据,则y关于x的经验回归方程为______________;
(2) 预计在今后的销售中,销量与单价仍然满足(1)中的关系,若该商品的成本是每件7.5元,为使商场获得最大利润,该商品的单价应定为________元.(利润=销售收入-成本)
5. (2024全国甲卷)某工厂进行生产线智能化升级改造,升级改造后,从该工厂甲、乙两个车间的产品中随机抽取150件进行检验,数据如下:
优级品 合格品 不合格品 合计
甲车间 26 24 0 50
乙车间 70 28 2 100
合计 96 52 2 150
(1) 填写如下列联表:
优级品 非优级品
甲车间
乙车间
能否有95%的把握认为甲、乙两车间产品的优级品率存在差异?能否有99%的把握认为甲,乙两车间产品的优级品率存在差异?
(2) 已知升级改造前该工厂产品的优级品率p=0.5,设为升级改造后抽取的n件产品的优级品率.如果 >p+1.65,则认为该工厂产品的优级品率提高了,根据抽取的150件产品的数据,能否认为生产线智能化升级改造后,该工厂产品的优级品率提高了?(参考数据:≈12.247)
附:χ2=,其中n=a+b+c+d.
α 0.050 0.010 0.001
xα 3.841 6.635 10.828
第八章 成对数据的统计分析
本 章 复 习
【活动方案】
例1 (1) 根据农户近5年种植药材的收入情况的统计数据可得=(1+2+3+4+5)=3,=(59+61+64+68+73)=65,
设t=x2,则y=bx2+a=bt+a,
所以=(12+22+32+42+52)=11,
则b==≈0.6,
a=-b=65-×11≈58.6.
故所求经验回归方程为y=0.6x2+58.6.
(2) 将x值代入可得估计值分别为59.2,61,64,68.2,73.6,
则残差平方和为(59-59.2)2+(61-61)2+(64-64)2+(68-68.2)2+(73-73.6)2=0.44.
因为0.44<0.5,
所以经验回归方程y=0.6x2+58.6拟合效果符合要求.
例2 建立性别与态度的2×2列联表如下:
肯定 否定 合计
男生 22 88 110
女生 22 38 60
合计 44 126 170
根据列联表中所给的数据,可求出男生中作肯定态度的频率为=0.2,女生中作肯定态度的频率为≈0.37.作等高堆积条形图如图,其中两个深色条形的高分别表示男生和女生中作肯定态度的频率,比较图中深色条形的高可以发现,女生中作肯定态度的频率明显高于男生中作肯定态度的频率,因此可以认为性别与态度有关系.
零假设为H0:性别和态度没有关系.
根据列联表中的数据得到
χ2=≈5.622>3.841=x0.05.
根据小概率值α=0.05的χ2独立性检验,我们推断H0不成立,即认为性别和态度有关系,此推断犯错误的概率不大于0.05.
【检测反馈】
1. A 观察选项可知,A中散点分布比较集中,且集合在某一条直线的附近,线性回归模型拟合效果比较好,呈现明显的正相关,故A中的样本相关系数最大.
2. C 因为==5,==4,所以4=1.2×5+,解得=-2,所以=1.2x-2.由z=ln y,得ln y=1.2x-2,所以,y=e1.2x-2=e-2·e1.2x,则c=e-2.
3. BCD 对于A,若所有样本点(xi,yi)都在直线y=0.95x+1上,则这组样本数据的样本相关系数为1,故A错误;对于B,由ξ~N(3,4),得D(ξ)=4.又ξ=2η+1,即η=ξ-,则D(η)=×D(ξ)=1,故B正确;对于C,在2×2列联表中,若每个数据a,b,c,d均变成原来的2倍,则χ2==,即χ2也变成原来的2倍,故C正确;对于D,分别抛掷2枚质地均匀的骰子,基本事件总数为6×6=36,事件A=“第一枚骰子正面向上的点数是奇数”,则事件A包含的基本事件数为3×6=18,事件B=“2枚骰子正面向上的点数相同”,则事件B包含的基本事件数为6×1=6,所以P(A)==,P(B)==.又事件AB包含的基本事件数为3×1=3,所以P(AB)==,所以P(AB)=P(A)×P(B),则A,B互为独立事件,故D正确.故选BCD.
4. (1)=-20x+250 设经验回归方程为=x+,由题意知,=×(8+8.2+8.4+8.6+8.8+9)=8.5,=×(90+84+83+80+75+68)=80,=-14,=0.7,所以==-20,=-=80+20×8.5=250,所以经验回归方程为=-20x+250.
(2) 10 设商场获得的利润为W元,由题意,得W=x(-20x+250)-7.5(-20x+250)=-20x2+400x-1 875=-20(x-10)2+125,当且仅当x=10时,W取得最大值,故当单价定为10元时,商场可获得最大利润.
5. (1) 根据题意可得列联表如下:
优级品 非优级品
甲车间 26 24
乙车间 70 30
可得χ2===4.687 5,
因为3.841<4.687 5<6.635,
所以有95%的把握认为甲、乙两车间产品的优级品率存在差异,没有99%的把握认为甲,乙两车间产品的优级品率存在差异.
(2) 由题意可知生产线智能化升级改造后,该工厂产品的优级品的频率为=0.64,
用频率估计概率可得=0.64,
又因为升级改造前该工厂产品的优级品率p=0.5,
所以p+1.65=0.5+1.65≈0.5+1.65×≈0.567,
可知>p+1.65,
所以可以认为生产线智能化升级改造后,该工厂产品的优级品率提高了.
