第十七章 勾股定理章末复习(二) 单元练习(含答案)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 第十七章 勾股定理章末复习(二) 单元练习(含答案)2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 184.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 07:43:24 | ||
图片预览


文档简介
勾股定理章末复习(二)
01 考点针对练
考点1 勾股定理的认识与证明
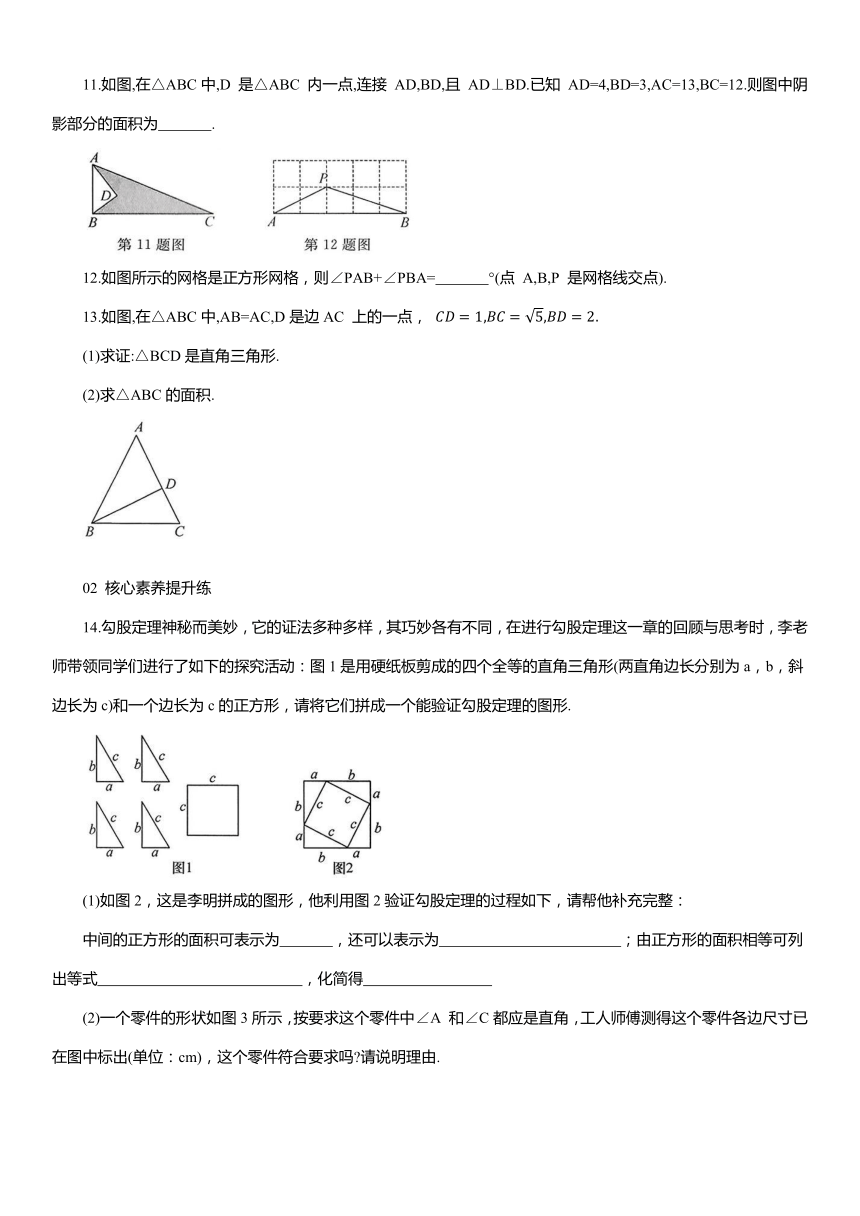
1.在学习勾股定理时,甲同学用四个相同的直角三角形(直角边长分别为a,b,斜边长为c)构成如图所示的正方形;乙同学用边长分别为a,b的两个正方形和长为b,宽为a的两个长方形构成如图所示的正方形.甲、乙两位同学给出的构图方案中,可以证明勾股定理的是 ( )
A.甲 B.乙
C.甲、乙都可以 D.甲、乙都不可以
考点2 勾股定理及其应用
2.如图,做一个长80 cm,宽60cm的长方形木框,需在相对角的顶点钉一根加固木条,则木条的长至少为 cm.
3. 新考向 跨学科(2024·吉林)图1中有一首古算诗,根据诗中的描述可以计算出红莲所在位置的湖水深度,其示意图如图2,其中AB=AB',AB⊥B'C 于点 C,BC=0.5尺,B'C=2尺.设AC的长度为x尺,可列方程为
4.(2023·大连)如图,在平面直角坐标系中,点A,B的坐标分别为(1,0)和(0,2),连接AB,以点 A 为圆心,AB的长为半径画弧,与x轴正半轴相交于点C,则点 C的横坐标是 .
5.(2023·东营)一艘船由 A 港沿北偏东 60°方向航行30 km至B港,然后再沿北偏西30°方向航行40 km至C港,则 A,C两港之间的距离为 .
6.(2024·眉山)如图,图1是北京国际数学家大会的会标,它取材于我国古代数学家赵爽的“弦图”,是由四个全等的直角三角形拼成.若图1中大正方形的面积为24,小正方形的面积为4,现将这四个直角三角形拼成图2所示的图形,则图2中大正方形的面积为 ( )
A.24 B.36 C.40 D.44
7.(2023·天津)如图,在△ABC中,分别以点 A和点C 为圆心,大于 AC的长为半径作弧(弧所在圆的半径都相等),两弧相交于 M,N两点,直线 MN 分别与边BC,AC 相交于点D,E,连接AD.若BD=DC,AE=4,AD=5,则AB的长为 ( )
A.9 B.8 C.7 D.6
8.已知线段a,b,c,且线段a,b满足
(1)求a,b的值.
(2)若a,b,c是某直角三角形的三条边的长,求c的值.
考点3 勾股定理的逆定理及其应用
9.如图,表格中是直角三角形的是 ( )
A.① B.② C.③ D.①②
10.在△ABC中,a,b,c分别是三边的长,下列说法:①∠B=∠C--∠A;②a =(b+c)(b-c);③∠A:∠B:∠C=3:4:5;④a:b:c=5:4: 3; 其中能判断△ABC为直角三角形的条件的个数为 ( )
A.2 B.3 C.4 D.5
11.如图,在△ABC中,D 是△ABC 内一点,连接 AD,BD,且 AD⊥BD.已知 AD=4,BD=3,AC=13,BC=12.则图中阴影部分的面积为 .
12.如图所示的网格是正方形网格,则∠PAB+∠PBA= °(点 A,B,P 是网格线交点).
13.如图,在△ABC中,AB=AC,D是边AC 上的一点,
(1)求证:△BCD是直角三角形.
(2)求△ABC的面积.
02 核心素养提升练
14.勾股定理神秘而美妙,它的证法多种多样,其巧妙各有不同,在进行勾股定理这一章的回顾与思考时,李老师带领同学们进行了如下的探究活动:图1是用硬纸板剪成的四个全等的直角三角形(两直角边长分别为a,b,斜边长为c)和一个边长为c的正方形,请将它们拼成一个能验证勾股定理的图形.
(1)如图2,这是李明拼成的图形,他利用图2验证勾股定理的过程如下,请帮他补充完整:
中间的正方形的面积可表示为 ,还可以表示为 ;由正方形的面积相等可列出等式 ,化简得
(2)一个零件的形状如图3所示,按要求这个零件中∠A 和∠C都应是直角,工人师傅测得这个零件各边尺寸已在图中标出(单位:cm),这个零件符合要求吗 请说明理由.
类型1 数学文化
1.(2024·大庆)如图1,直角三角形的两个锐角分别是 40°和 50°,其三边上分别有一个正方形.执行下面的操作:由两个小正方形向外分别作锐角为 40°和 50°的直角三角形,再分别以所得到的直角三角形的直角边为边长作正方形.图2是1次操作后的图形.图3 是重复上述步骤若干次后得到的图形,人们把它称为“毕达哥拉斯树”.若图1中的直角三角形斜边长为2,则10次操作后图形中所有正方形的面积和为 .
类型2 阅读理解问题
2.阅读材料:勾股定理是平面几何中一个极为重要的定理,在对它的证明方法中很多都用到了出入相补原理:把一个平面图形从一处移至它处,面积不变;如果把图形分割成几块,那么各部分面积之和等于原来图形的面积.
解决问题:小红用硬纸板做成了如图1所示的两个全等的直角三角形,两直角边的长分别为a和b,斜边为c,和一个以c为直角边的等腰直角三角形,然后把它们拼成了如图2所示的一个直角梯形,
(1)请根据小红的操作,利用下面的图形证明勾股定理.
(2)若a=7 cm,b=24 cm,求△ADE的面积.
类型3 综合与实践
3.【问题情境】某数学兴趣小组想测量学校旗杆的高度.
【实践发现】数学兴趣小组实地勘查发现:系在旗杆顶端的绳子垂到了地面,并多出了一段,但这条绳子的长度未知.
【实践探究】设计测量方案:
第一步:先测量比旗杆多出的部分绳子的长度,测得多出部分绳子的长度是1 米.
第二步:把绳子向外拉直,绳子的底端恰好接触地面的点C,再测量绳子底端C与旗杆根部B点之间的距离,测得距离为5 米.
【问题解决】设旗杆的高度 AB=x米,通过计算即可求得旗杆的高度.
(1)依题知 BC= 米,AC= 米(用含x的式子表示).
(2)求旗杆的高度.
章末复习(二) 勾股定理
1. A 2.100 3. x +2 =(x+0.5) 4. +1 5.50 km 6. D7. D
8.解:() (2)分两种情况讨论:①当a,b为直角三角形的两条直角边时, ②当a为直角三角形的斜边时, 6.综上所述,c的值为2 或6.
9. B 10. C11.24 12.45
13.解:(1)证明:∵CD=1,BC= ,BD=2,∴CD +BD =1 +2 =5=BC .∴△BCD是直角三角形.(2)设腰长 AB=AC=x.在Rt△ADB中,由勾股定理,得 即 2 ,解得
14.解 , (2)这个零件不符合要求.理由如下: 20 =225+400=625=BD ,∴△BCD是直角三角形,且∠C= 不是直角三角形,∠A 不是直角.∴这个零件不符合要求.
新课标·新情境·新题型·引领训练
1.48
2.解:(1)证明: b + ab.∴c =a +b .(2)∵△ABE是直角三角形,a=7 cm,b=
3.解:(1)5 ((x+1) (2)在 Rt△ABC中,由勾股定理,得. =AC ,即 解得x=12.答:旗杆的高度为12米.
01 考点针对练
考点1 勾股定理的认识与证明
1.在学习勾股定理时,甲同学用四个相同的直角三角形(直角边长分别为a,b,斜边长为c)构成如图所示的正方形;乙同学用边长分别为a,b的两个正方形和长为b,宽为a的两个长方形构成如图所示的正方形.甲、乙两位同学给出的构图方案中,可以证明勾股定理的是 ( )
A.甲 B.乙
C.甲、乙都可以 D.甲、乙都不可以
考点2 勾股定理及其应用
2.如图,做一个长80 cm,宽60cm的长方形木框,需在相对角的顶点钉一根加固木条,则木条的长至少为 cm.
3. 新考向 跨学科(2024·吉林)图1中有一首古算诗,根据诗中的描述可以计算出红莲所在位置的湖水深度,其示意图如图2,其中AB=AB',AB⊥B'C 于点 C,BC=0.5尺,B'C=2尺.设AC的长度为x尺,可列方程为
4.(2023·大连)如图,在平面直角坐标系中,点A,B的坐标分别为(1,0)和(0,2),连接AB,以点 A 为圆心,AB的长为半径画弧,与x轴正半轴相交于点C,则点 C的横坐标是 .
5.(2023·东营)一艘船由 A 港沿北偏东 60°方向航行30 km至B港,然后再沿北偏西30°方向航行40 km至C港,则 A,C两港之间的距离为 .
6.(2024·眉山)如图,图1是北京国际数学家大会的会标,它取材于我国古代数学家赵爽的“弦图”,是由四个全等的直角三角形拼成.若图1中大正方形的面积为24,小正方形的面积为4,现将这四个直角三角形拼成图2所示的图形,则图2中大正方形的面积为 ( )
A.24 B.36 C.40 D.44
7.(2023·天津)如图,在△ABC中,分别以点 A和点C 为圆心,大于 AC的长为半径作弧(弧所在圆的半径都相等),两弧相交于 M,N两点,直线 MN 分别与边BC,AC 相交于点D,E,连接AD.若BD=DC,AE=4,AD=5,则AB的长为 ( )
A.9 B.8 C.7 D.6
8.已知线段a,b,c,且线段a,b满足
(1)求a,b的值.
(2)若a,b,c是某直角三角形的三条边的长,求c的值.
考点3 勾股定理的逆定理及其应用
9.如图,表格中是直角三角形的是 ( )
A.① B.② C.③ D.①②
10.在△ABC中,a,b,c分别是三边的长,下列说法:①∠B=∠C--∠A;②a =(b+c)(b-c);③∠A:∠B:∠C=3:4:5;④a:b:c=5:4: 3; 其中能判断△ABC为直角三角形的条件的个数为 ( )
A.2 B.3 C.4 D.5
11.如图,在△ABC中,D 是△ABC 内一点,连接 AD,BD,且 AD⊥BD.已知 AD=4,BD=3,AC=13,BC=12.则图中阴影部分的面积为 .
12.如图所示的网格是正方形网格,则∠PAB+∠PBA= °(点 A,B,P 是网格线交点).
13.如图,在△ABC中,AB=AC,D是边AC 上的一点,
(1)求证:△BCD是直角三角形.
(2)求△ABC的面积.
02 核心素养提升练
14.勾股定理神秘而美妙,它的证法多种多样,其巧妙各有不同,在进行勾股定理这一章的回顾与思考时,李老师带领同学们进行了如下的探究活动:图1是用硬纸板剪成的四个全等的直角三角形(两直角边长分别为a,b,斜边长为c)和一个边长为c的正方形,请将它们拼成一个能验证勾股定理的图形.
(1)如图2,这是李明拼成的图形,他利用图2验证勾股定理的过程如下,请帮他补充完整:
中间的正方形的面积可表示为 ,还可以表示为 ;由正方形的面积相等可列出等式 ,化简得
(2)一个零件的形状如图3所示,按要求这个零件中∠A 和∠C都应是直角,工人师傅测得这个零件各边尺寸已在图中标出(单位:cm),这个零件符合要求吗 请说明理由.
类型1 数学文化
1.(2024·大庆)如图1,直角三角形的两个锐角分别是 40°和 50°,其三边上分别有一个正方形.执行下面的操作:由两个小正方形向外分别作锐角为 40°和 50°的直角三角形,再分别以所得到的直角三角形的直角边为边长作正方形.图2是1次操作后的图形.图3 是重复上述步骤若干次后得到的图形,人们把它称为“毕达哥拉斯树”.若图1中的直角三角形斜边长为2,则10次操作后图形中所有正方形的面积和为 .
类型2 阅读理解问题
2.阅读材料:勾股定理是平面几何中一个极为重要的定理,在对它的证明方法中很多都用到了出入相补原理:把一个平面图形从一处移至它处,面积不变;如果把图形分割成几块,那么各部分面积之和等于原来图形的面积.
解决问题:小红用硬纸板做成了如图1所示的两个全等的直角三角形,两直角边的长分别为a和b,斜边为c,和一个以c为直角边的等腰直角三角形,然后把它们拼成了如图2所示的一个直角梯形,
(1)请根据小红的操作,利用下面的图形证明勾股定理.
(2)若a=7 cm,b=24 cm,求△ADE的面积.
类型3 综合与实践
3.【问题情境】某数学兴趣小组想测量学校旗杆的高度.
【实践发现】数学兴趣小组实地勘查发现:系在旗杆顶端的绳子垂到了地面,并多出了一段,但这条绳子的长度未知.
【实践探究】设计测量方案:
第一步:先测量比旗杆多出的部分绳子的长度,测得多出部分绳子的长度是1 米.
第二步:把绳子向外拉直,绳子的底端恰好接触地面的点C,再测量绳子底端C与旗杆根部B点之间的距离,测得距离为5 米.
【问题解决】设旗杆的高度 AB=x米,通过计算即可求得旗杆的高度.
(1)依题知 BC= 米,AC= 米(用含x的式子表示).
(2)求旗杆的高度.
章末复习(二) 勾股定理
1. A 2.100 3. x +2 =(x+0.5) 4. +1 5.50 km 6. D7. D
8.解:() (2)分两种情况讨论:①当a,b为直角三角形的两条直角边时, ②当a为直角三角形的斜边时, 6.综上所述,c的值为2 或6.
9. B 10. C11.24 12.45
13.解:(1)证明:∵CD=1,BC= ,BD=2,∴CD +BD =1 +2 =5=BC .∴△BCD是直角三角形.(2)设腰长 AB=AC=x.在Rt△ADB中,由勾股定理,得 即 2 ,解得
14.解 , (2)这个零件不符合要求.理由如下: 20 =225+400=625=BD ,∴△BCD是直角三角形,且∠C= 不是直角三角形,∠A 不是直角.∴这个零件不符合要求.
新课标·新情境·新题型·引领训练
1.48
2.解:(1)证明: b + ab.∴c =a +b .(2)∵△ABE是直角三角形,a=7 cm,b=
3.解:(1)5 ((x+1) (2)在 Rt△ABC中,由勾股定理,得. =AC ,即 解得x=12.答:旗杆的高度为12米.
