17.1 勾股定理 分层练习(含答案)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 17.1 勾股定理 分层练习(含答案)2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 340.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 07:47:46 | ||
图片预览


文档简介
17.1 勾股定理
第1课时 勾股定理
A基础题
知识点1 勾股定理的认识
1.如图,这是由边长均为1的正方形组成的网格,下面是“勾股定理”的探索与验证过程,请补充完整:
即
2. 新考向 数学文化如图,“赵爽弦图”是由四个全等的直角三角形(阴影部分)围成一个大正方形,中空的部分是一个小正方形.它是我国汉代的赵爽在注解《周髀算经》时给出的,其巧妙地利用图形的面积证明了“勾股定理”,体现了我国古人的聪明才智和对数学的钻研精神,是我国古代数学的骄傲.
(1)请写出“勾股定理”的内容.
(2)请利用图形面积,结合图形完成“勾股定理”的证明.
知识点2 利用勾股定理进行计算
3.求出下列直角三角形中未知边的长度.
x= y=
4.在 Rt△ABC中,∠A=90°,AC=3,AB=4,则 BC的长为 ( )
A. B.3
C.5 或 D.5
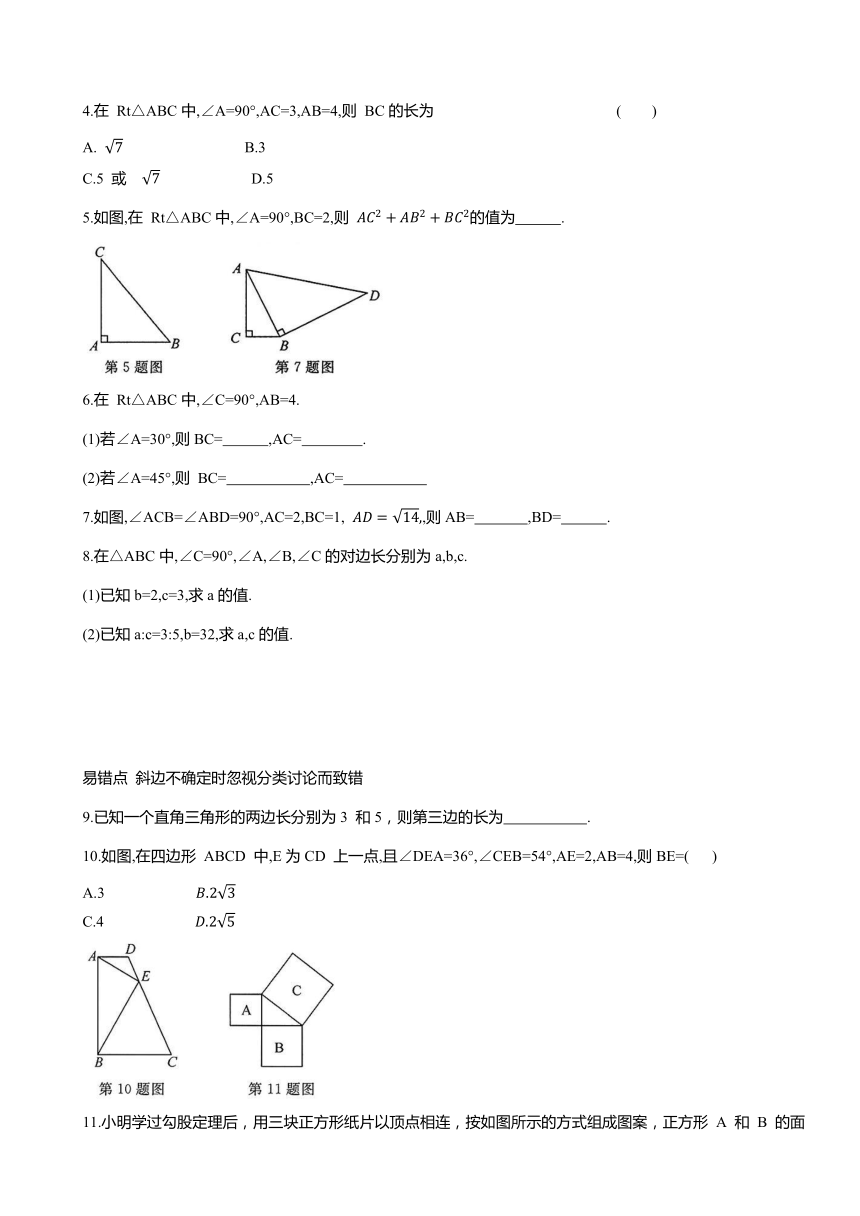
5.如图,在 Rt△ABC中,∠A=90°,BC=2,则 的值为 .
6.在 Rt△ABC中,∠C=90°,AB=4.
(1)若∠A=30°,则BC= ,AC= .
(2)若∠A=45°,则 BC= ,AC=
7.如图,∠ACB=∠ABD=90°,AC=2,BC=1, ,则AB= ,BD= .
8.在△ABC中,∠C=90°,∠A,∠B,∠C的对边长分别为a,b,c.
(1)已知b=2,c=3,求a的值.
(2)已知a:c=3:5,b=32,求a,c的值.
易错点 斜边不确定时忽视分类讨论而致错
9.已知一个直角三角形的两边长分别为3 和5,则第三边的长为 .
10.如图,在四边形 ABCD 中,E为CD 上一点,且∠DEA=36°,∠CEB=54°,AE=2,AB=4,则BE=( )
A.3
C.4
11.小明学过勾股定理后,用三块正方形纸片以顶点相连,按如图所示的方式组成图案,正方形 A 和 B 的面积分别为3 和4.若使所围成的三角形是直角三角形,则正方形C的边长为 ( )
A.5 B.6 C. D.
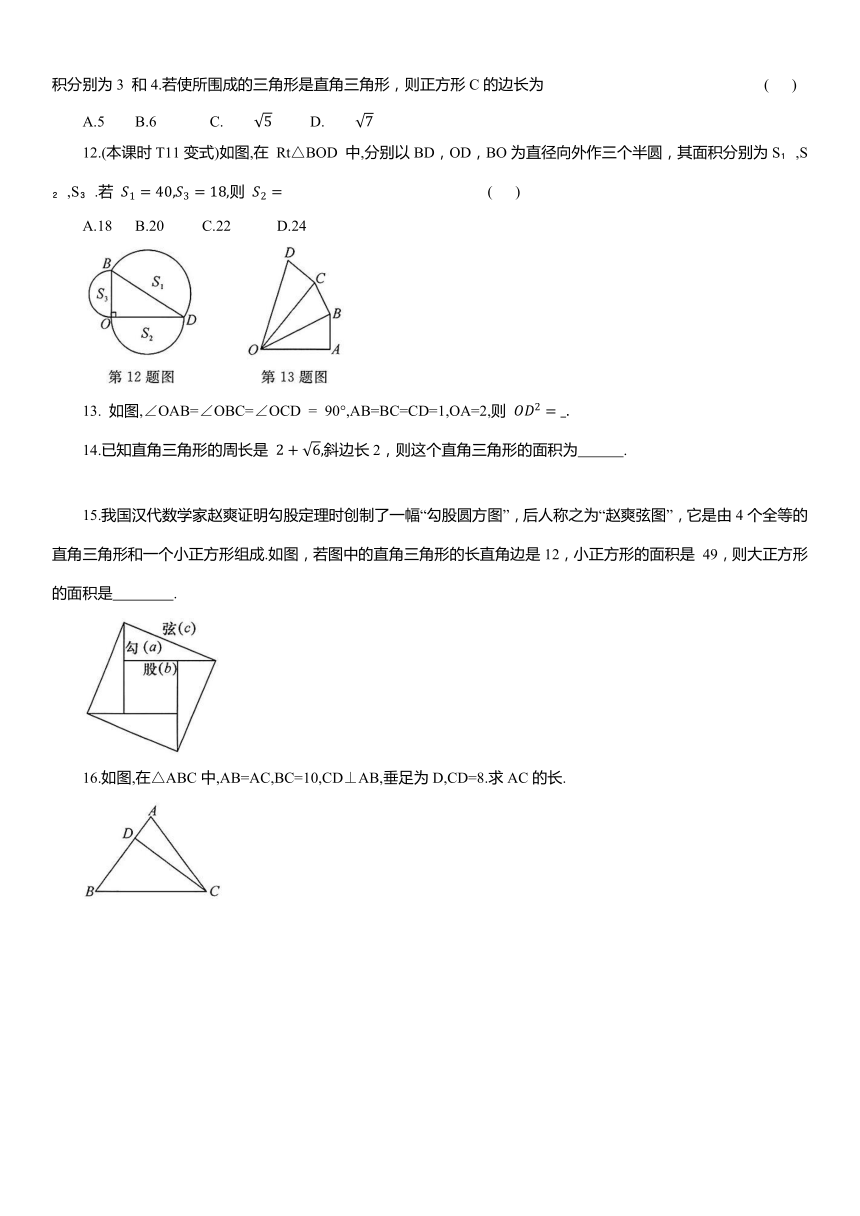
12.(本课时T11变式)如图,在 Rt△BOD 中,分别以BD,OD,BO为直径向外作三个半圆,其面积分别为S ,S ,S .若 则 ( )
A.18 B.20 C.22 D.24
13. 如图,∠OAB=∠OBC=∠OCD = 90°,AB=BC=CD=1,OA=2,则
14.已知直角三角形的周长是 斜边长2,则这个直角三角形的面积为 .
15.我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”,后人称之为“赵爽弦图”,它是由4个全等的直角三角形和一个小正方形组成.如图,若图中的直角三角形的长直角边是12,小正方形的面积是 49,则大正方形的面积是 .
16.如图,在△ABC中,AB=AC,BC=10,CD⊥AB,垂足为D,CD=8.求AC的长.
C 综合题
17.如图,在四边形ABCD中,∠DAB=∠BCD=90°,分别以四边形 ABCD 的四条边为边向外作四个正方形,面积分别为a,b,c,d,且cA. d=10
C.四边形ABCD的面积是24
D. AD第 2课时 勾股定理的应用
A基础题
知识点 勾股定理的应用
1.如图,一辆货车车厢底部离地面的高度 AB 为1.5m,为了方便卸货,常用一块木板AC搭成一个斜面.已知BC=2m,则木板AC的长为( )
A. 2m B.2. 2m C.3m D.2. 5m
2.如图,将一支笔放到圆柱形笔筒中,笔筒内部底面直径是 9 cm,内壁高 12 cm.若这支笔长18 cm,则这支笔在笔筒外面部分的长度是( )
A.6 cm B. 5cm C. 3cm D. 2cm
3.如图,一棵大树在一次强台风中在距地面5m处折断,倒下后树顶端着地点 A 距树底端B的距离为12 m,则这棵大树在折断前的高度为 ( )
A.10m B.17m C.18m D.2 0 m
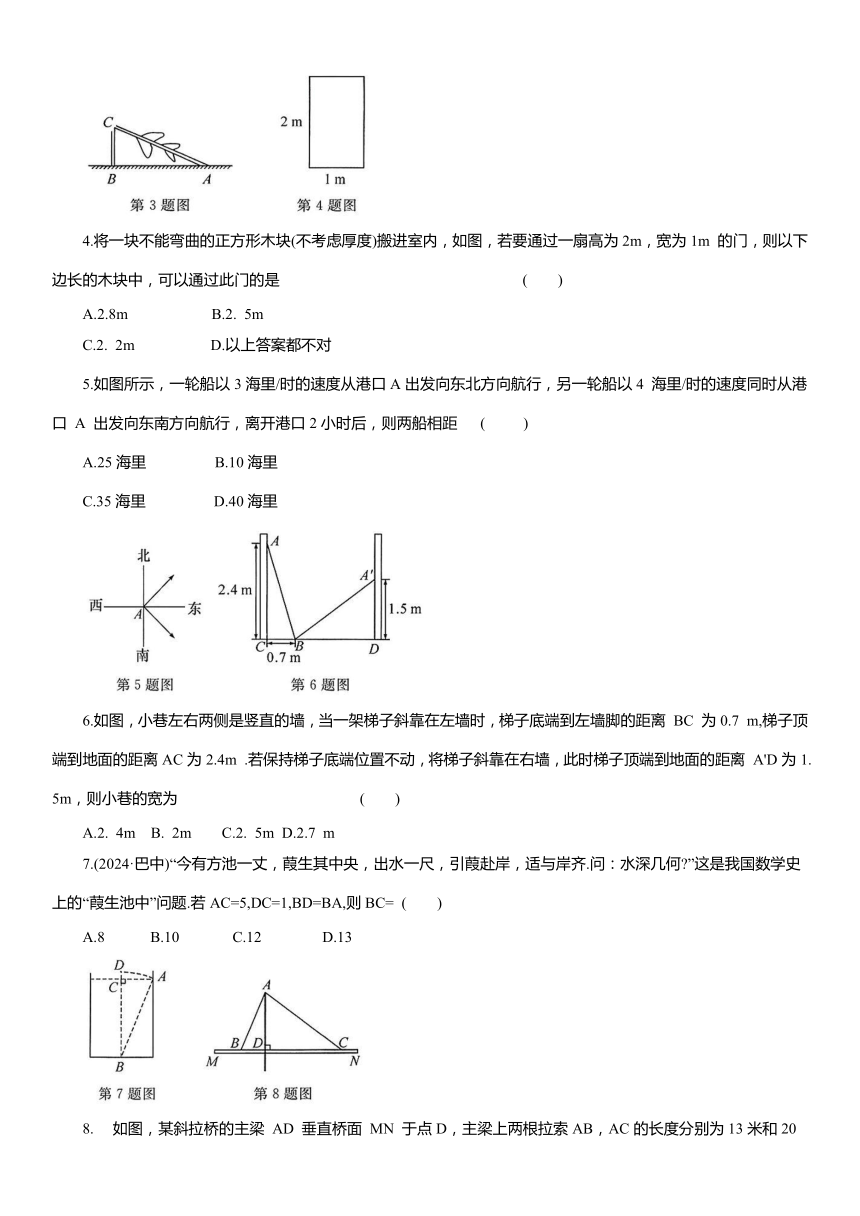
4.将一块不能弯曲的正方形木块(不考虑厚度)搬进室内,如图,若要通过一扇高为2m,宽为1m 的门,则以下边长的木块中,可以通过此门的是 ( )
A.2.8m B.2. 5m
C.2. 2m D.以上答案都不对
5.如图所示,一轮船以3海里/时的速度从港口A出发向东北方向航行,另一轮船以4 海里/时的速度同时从港口 A 出发向东南方向航行,离开港口2小时后,则两船相距 ( )
A.25海里 B.10海里
C.35海里 D.40海里
6.如图,小巷左右两侧是竖直的墙,当一架梯子斜靠在左墙时,梯子底端到左墙脚的距离 BC 为0.7 m,梯子顶端到地面的距离AC为2.4m .若保持梯子底端位置不动,将梯子斜靠在右墙,此时梯子顶端到地面的距离 A'D为1.5m,则小巷的宽为 ( )
A.2. 4m B. 2m C.2. 5m D.2.7 m
7.(2024·巴中)“今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问:水深几何 ”这是我国数学史上的“葭生池中”问题.若AC=5,DC=1,BD=BA,则BC= ( )
A.8 B.10 C.12 D.13
如图,某斜拉桥的主梁 AD 垂直桥面 MN 于点D,主梁上两根拉索AB,AC的长度分别为13米和20米,主梁AD的高度为12米,则固定点B,C之间的距离为 米.
9.根据规定,小汽车在城市街道上行驶的速度不得超过70 km/h.如图,一辆小汽车在一条城市街道上直行,某一时刻刚好行驶到路边车速检测仪A处的正前方30 m的点 C处,过了2 s后,测得小汽车与车速检测仪之间的距离为50 m,则这辆小汽车超速了吗 请说明理由.
B 中档题
10.如图,某超市为了吸引顾客,在超市门口离地高4.5m的墙上,装有一个由传感器控制的门铃A,如图1所示,人只要移至该门铃5m 及5m以内时,门铃就会自动发出语音“欢迎光临”,如图2 所示,一个身高1.5m的学生走到D处,门铃恰好自动响起,则BD 的长为 ( )
A. 3m B. 4m C. 5m D.7m
11.如图所示,梯子 AB 靠在墙上,梯子的顶端 A 到墙根O的距离为24m,梯子的底端B到墙根O的距离为7 m.若梯子顶端A下滑4m到C,底端B滑动到 D,则 BD 的长是 m.
12.如图,这是楼梯的侧面示意图,楼梯的宽为5m,AC=5m,AB=13 m.若在楼梯上铺设防滑材料,则所需防滑材料的面积至少为 m .
13.如图,已知树 EF(垂直于地面)上的点 B 处(BE=5米)有两只松鼠,为抢到A处(点 A,E在同一水平地面上,AE=10米)的坚果,一只松鼠沿B-E-A到达点 A 处,另一只松鼠沿B-F-A到达点 A处.若两只松鼠经过的路程相等,则树 EF 的高度为 米.
14.如图,有一架秋千,当它静止在 AD的位置时,踏板离地面的垂直高度为0.6m,将秋千AD往前推送3m,到达 AB 的位置,此时秋千的踏板离地面的垂直高度为1.6m,秋千的绳索始终保持拉直的状态.
(1)BF= m,BC= m,CD= m.
(2)根据(1)中求得的数据,求秋千的长度.
(3)如果想要踏板离地面的垂直高度为2.6m,那么需要将秋千 AD往前推送 m.
C 综合题
15.如图,在 Rt△ABC中,∠ACB=90°,AB=5cm,AC=3 cm,动点 P 从点 B 出发沿射线BC 以 1 cm/s的速度运动.设运动的时间为ts,当△ABP 为等腰三角形时,t 的值为
第 3课时 利用勾股定理作图
A基础题
知识点1 勾股定理与数轴、坐标轴
1.如图,点A 表示的实数是 ( )
A. B.
2.如图,在平面直角坐标系中,以点 O为圆心,OP 的长为半径画弧,交x 轴的负半轴于点A.若点 A 的坐标为( ,点P 的纵坐标为--1,则点 P 的坐标为 .
3.如图,四边形OEBC为正方形.
(1)图中的点 A 表示的数是 .
(2)在图中画出表示 的点 M.
知识点2 勾股定理与网格
4.如图,在3×4的正方形网格(每个小正方形的边长都是1)中,标记格点(网格线的交点)A,B,C,D,则下列线段中,长度为 的是( )
A.线段AB B.线段 BC
C.线段AC D.线段 BD
5.如图,△ABC的顶点A,B,C在边长为1的正方形网格的格点(网格线的交点)上,BD⊥AC于点D,则 BD的长为 ( )
A. B.
C. D.
6.如图,正方形网格中的每个小正方形边长都是1,任意连接这些小正方形的顶点,可得到一些线段.请在图中画出线段
知识点3 勾股定理与图形的计算
7.如图,已知△ABO为等边三角形,边长为6,则点 A 的坐标为 .
8.如图,在 Rt△ABC中,∠ABC=90°,AC=4,BC=2,以点C为圆心,BC的长为半径画弧,交AC于点 D,以点 A 为圆心,AD 的长为半径画弧,交AB于点E,则BE= .
9. 如图,在 △ABC 中,∠C = 90°, AD 平分∠CAB,DE⊥AB 于点 E.若 DE=15 cm,BE=8cm ,则 BC的长为 cm.
易错点 三角形的形状不确定而漏解
10.在△ABC中,AB=25,AC=30,高AD=24,则 BC的长为 .
11.如图,在平面直角坐标系中,点A 的坐标为(6,4),以点O为圆心,OA的长为半径画弧,交x轴的正半轴于点 B,则点 B 的横坐标介于 ( )
A.5 和6 之间
B.7 和8之间
C.10 和11之间
D.8 和9 之间
12.为了比较 与 的大小,可以构造如图所示的图形进行推算,其中∠C=90°,BC=3,点D在BC上,且BD=AC=1.通过计算可得 (填“>”“<”或“=”).
13.在如图所示的象棋盘中,每个小正方形的边长均为1.“马”从图中的位置出发,不走重复路线,按照“马走日”的规则,走两步后的落点与出发点间的最短距离为 .
14.如图,在4×4的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.
(1)在图 1 中,以格点为顶点画△ABC,使△ABC的三边长分别为3,4,5.
(2)在图 2 中,以格点为顶点画△DEF,使△DEF的三边长分别为
C 综合题
15.图甲是第七届国际数学教育大会的会徽,会徽的主体图案是由图乙中的一连串直角三角形 演化而成的,其中 细心观察图形,认真分析下列各式,然后解答问题:
……
(1)请用含 n(n是正整数)的等式表示上述变化规律,并计算出OA 的长.
(2)求出 的值.
17.1 勾股定理
第1课时勾股定理
1.4 9 13 AC BC AB
2.解:(1)在直角三角形中,两条直角边的平方和等于斜边的平方.(2)证明:由图可知, .在直角三角形中,两条直角边的平方和等于斜边的平方.
3.10 4. D 5.8 6.(1)2 2 (2)2 2 7.
8.解:(1)∵在△ABC中,∠C=90°,b=2,c=3,∴a=√c -b = (2)设a=3x,则 解得x=8(负值舍去).∴3x=24,5x=40,即a=24,c=40.
9.4或 10. B 11. D 12. C 13.7 14. 15.169
16.解:∵CD⊥AB,∴∠ADC=∠BDC=90°.在 Rt△BCD中,BD= .设AC=AB=x,则AD=x--6.在Rt△ACD中, 即 解得
17. C
第2课时勾股定理的应用
1. D 2. C 3. C 4. C 5. B 6. D 7. C 8.21
9.解:这辆小汽车超速了,理由如下:在 Rt△ABC中,∠C=90°,AC=30m,AB=50 m,根据勾股定理,得 ∴小汽车的速度 ∴这辆小汽车超速了.
10. B11.8 12.85 13.7.5
14.解:(1)1.6 3 1 (2)∵BC⊥AC,∴∠ACB=90°.设秋千的长度为 xm,则AB=AD=xm,AC=AD--CD=(x--1)m.在Rt△ABC中,由勾股定理,得 即 x ,解得x=5.答:秋千的长度是5m .(3)4
15.5或8或
第3课时利用勾股定理作图
1. C 2.(-4,-1)
3.解:(1) (2)图略.
4. B5. C
6.解:图略.
7.(-3,3 8.2 -2 9.32 10.11 或25 11. B 12.<
13.
14.解:图略.
15.解:
第1课时 勾股定理
A基础题
知识点1 勾股定理的认识
1.如图,这是由边长均为1的正方形组成的网格,下面是“勾股定理”的探索与验证过程,请补充完整:
即
2. 新考向 数学文化如图,“赵爽弦图”是由四个全等的直角三角形(阴影部分)围成一个大正方形,中空的部分是一个小正方形.它是我国汉代的赵爽在注解《周髀算经》时给出的,其巧妙地利用图形的面积证明了“勾股定理”,体现了我国古人的聪明才智和对数学的钻研精神,是我国古代数学的骄傲.
(1)请写出“勾股定理”的内容.
(2)请利用图形面积,结合图形完成“勾股定理”的证明.
知识点2 利用勾股定理进行计算
3.求出下列直角三角形中未知边的长度.
x= y=
4.在 Rt△ABC中,∠A=90°,AC=3,AB=4,则 BC的长为 ( )
A. B.3
C.5 或 D.5
5.如图,在 Rt△ABC中,∠A=90°,BC=2,则 的值为 .
6.在 Rt△ABC中,∠C=90°,AB=4.
(1)若∠A=30°,则BC= ,AC= .
(2)若∠A=45°,则 BC= ,AC=
7.如图,∠ACB=∠ABD=90°,AC=2,BC=1, ,则AB= ,BD= .
8.在△ABC中,∠C=90°,∠A,∠B,∠C的对边长分别为a,b,c.
(1)已知b=2,c=3,求a的值.
(2)已知a:c=3:5,b=32,求a,c的值.
易错点 斜边不确定时忽视分类讨论而致错
9.已知一个直角三角形的两边长分别为3 和5,则第三边的长为 .
10.如图,在四边形 ABCD 中,E为CD 上一点,且∠DEA=36°,∠CEB=54°,AE=2,AB=4,则BE=( )
A.3
C.4
11.小明学过勾股定理后,用三块正方形纸片以顶点相连,按如图所示的方式组成图案,正方形 A 和 B 的面积分别为3 和4.若使所围成的三角形是直角三角形,则正方形C的边长为 ( )
A.5 B.6 C. D.
12.(本课时T11变式)如图,在 Rt△BOD 中,分别以BD,OD,BO为直径向外作三个半圆,其面积分别为S ,S ,S .若 则 ( )
A.18 B.20 C.22 D.24
13. 如图,∠OAB=∠OBC=∠OCD = 90°,AB=BC=CD=1,OA=2,则
14.已知直角三角形的周长是 斜边长2,则这个直角三角形的面积为 .
15.我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”,后人称之为“赵爽弦图”,它是由4个全等的直角三角形和一个小正方形组成.如图,若图中的直角三角形的长直角边是12,小正方形的面积是 49,则大正方形的面积是 .
16.如图,在△ABC中,AB=AC,BC=10,CD⊥AB,垂足为D,CD=8.求AC的长.
C 综合题
17.如图,在四边形ABCD中,∠DAB=∠BCD=90°,分别以四边形 ABCD 的四条边为边向外作四个正方形,面积分别为a,b,c,d,且c
C.四边形ABCD的面积是24
D. AD
A基础题
知识点 勾股定理的应用
1.如图,一辆货车车厢底部离地面的高度 AB 为1.5m,为了方便卸货,常用一块木板AC搭成一个斜面.已知BC=2m,则木板AC的长为( )
A. 2m B.2. 2m C.3m D.2. 5m
2.如图,将一支笔放到圆柱形笔筒中,笔筒内部底面直径是 9 cm,内壁高 12 cm.若这支笔长18 cm,则这支笔在笔筒外面部分的长度是( )
A.6 cm B. 5cm C. 3cm D. 2cm
3.如图,一棵大树在一次强台风中在距地面5m处折断,倒下后树顶端着地点 A 距树底端B的距离为12 m,则这棵大树在折断前的高度为 ( )
A.10m B.17m C.18m D.2 0 m
4.将一块不能弯曲的正方形木块(不考虑厚度)搬进室内,如图,若要通过一扇高为2m,宽为1m 的门,则以下边长的木块中,可以通过此门的是 ( )
A.2.8m B.2. 5m
C.2. 2m D.以上答案都不对
5.如图所示,一轮船以3海里/时的速度从港口A出发向东北方向航行,另一轮船以4 海里/时的速度同时从港口 A 出发向东南方向航行,离开港口2小时后,则两船相距 ( )
A.25海里 B.10海里
C.35海里 D.40海里
6.如图,小巷左右两侧是竖直的墙,当一架梯子斜靠在左墙时,梯子底端到左墙脚的距离 BC 为0.7 m,梯子顶端到地面的距离AC为2.4m .若保持梯子底端位置不动,将梯子斜靠在右墙,此时梯子顶端到地面的距离 A'D为1.5m,则小巷的宽为 ( )
A.2. 4m B. 2m C.2. 5m D.2.7 m
7.(2024·巴中)“今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问:水深几何 ”这是我国数学史上的“葭生池中”问题.若AC=5,DC=1,BD=BA,则BC= ( )
A.8 B.10 C.12 D.13
如图,某斜拉桥的主梁 AD 垂直桥面 MN 于点D,主梁上两根拉索AB,AC的长度分别为13米和20米,主梁AD的高度为12米,则固定点B,C之间的距离为 米.
9.根据规定,小汽车在城市街道上行驶的速度不得超过70 km/h.如图,一辆小汽车在一条城市街道上直行,某一时刻刚好行驶到路边车速检测仪A处的正前方30 m的点 C处,过了2 s后,测得小汽车与车速检测仪之间的距离为50 m,则这辆小汽车超速了吗 请说明理由.
B 中档题
10.如图,某超市为了吸引顾客,在超市门口离地高4.5m的墙上,装有一个由传感器控制的门铃A,如图1所示,人只要移至该门铃5m 及5m以内时,门铃就会自动发出语音“欢迎光临”,如图2 所示,一个身高1.5m的学生走到D处,门铃恰好自动响起,则BD 的长为 ( )
A. 3m B. 4m C. 5m D.7m
11.如图所示,梯子 AB 靠在墙上,梯子的顶端 A 到墙根O的距离为24m,梯子的底端B到墙根O的距离为7 m.若梯子顶端A下滑4m到C,底端B滑动到 D,则 BD 的长是 m.
12.如图,这是楼梯的侧面示意图,楼梯的宽为5m,AC=5m,AB=13 m.若在楼梯上铺设防滑材料,则所需防滑材料的面积至少为 m .
13.如图,已知树 EF(垂直于地面)上的点 B 处(BE=5米)有两只松鼠,为抢到A处(点 A,E在同一水平地面上,AE=10米)的坚果,一只松鼠沿B-E-A到达点 A 处,另一只松鼠沿B-F-A到达点 A处.若两只松鼠经过的路程相等,则树 EF 的高度为 米.
14.如图,有一架秋千,当它静止在 AD的位置时,踏板离地面的垂直高度为0.6m,将秋千AD往前推送3m,到达 AB 的位置,此时秋千的踏板离地面的垂直高度为1.6m,秋千的绳索始终保持拉直的状态.
(1)BF= m,BC= m,CD= m.
(2)根据(1)中求得的数据,求秋千的长度.
(3)如果想要踏板离地面的垂直高度为2.6m,那么需要将秋千 AD往前推送 m.
C 综合题
15.如图,在 Rt△ABC中,∠ACB=90°,AB=5cm,AC=3 cm,动点 P 从点 B 出发沿射线BC 以 1 cm/s的速度运动.设运动的时间为ts,当△ABP 为等腰三角形时,t 的值为
第 3课时 利用勾股定理作图
A基础题
知识点1 勾股定理与数轴、坐标轴
1.如图,点A 表示的实数是 ( )
A. B.
2.如图,在平面直角坐标系中,以点 O为圆心,OP 的长为半径画弧,交x 轴的负半轴于点A.若点 A 的坐标为( ,点P 的纵坐标为--1,则点 P 的坐标为 .
3.如图,四边形OEBC为正方形.
(1)图中的点 A 表示的数是 .
(2)在图中画出表示 的点 M.
知识点2 勾股定理与网格
4.如图,在3×4的正方形网格(每个小正方形的边长都是1)中,标记格点(网格线的交点)A,B,C,D,则下列线段中,长度为 的是( )
A.线段AB B.线段 BC
C.线段AC D.线段 BD
5.如图,△ABC的顶点A,B,C在边长为1的正方形网格的格点(网格线的交点)上,BD⊥AC于点D,则 BD的长为 ( )
A. B.
C. D.
6.如图,正方形网格中的每个小正方形边长都是1,任意连接这些小正方形的顶点,可得到一些线段.请在图中画出线段
知识点3 勾股定理与图形的计算
7.如图,已知△ABO为等边三角形,边长为6,则点 A 的坐标为 .
8.如图,在 Rt△ABC中,∠ABC=90°,AC=4,BC=2,以点C为圆心,BC的长为半径画弧,交AC于点 D,以点 A 为圆心,AD 的长为半径画弧,交AB于点E,则BE= .
9. 如图,在 △ABC 中,∠C = 90°, AD 平分∠CAB,DE⊥AB 于点 E.若 DE=15 cm,BE=8cm ,则 BC的长为 cm.
易错点 三角形的形状不确定而漏解
10.在△ABC中,AB=25,AC=30,高AD=24,则 BC的长为 .
11.如图,在平面直角坐标系中,点A 的坐标为(6,4),以点O为圆心,OA的长为半径画弧,交x轴的正半轴于点 B,则点 B 的横坐标介于 ( )
A.5 和6 之间
B.7 和8之间
C.10 和11之间
D.8 和9 之间
12.为了比较 与 的大小,可以构造如图所示的图形进行推算,其中∠C=90°,BC=3,点D在BC上,且BD=AC=1.通过计算可得 (填“>”“<”或“=”).
13.在如图所示的象棋盘中,每个小正方形的边长均为1.“马”从图中的位置出发,不走重复路线,按照“马走日”的规则,走两步后的落点与出发点间的最短距离为 .
14.如图,在4×4的正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫做格点.
(1)在图 1 中,以格点为顶点画△ABC,使△ABC的三边长分别为3,4,5.
(2)在图 2 中,以格点为顶点画△DEF,使△DEF的三边长分别为
C 综合题
15.图甲是第七届国际数学教育大会的会徽,会徽的主体图案是由图乙中的一连串直角三角形 演化而成的,其中 细心观察图形,认真分析下列各式,然后解答问题:
……
(1)请用含 n(n是正整数)的等式表示上述变化规律,并计算出OA 的长.
(2)求出 的值.
17.1 勾股定理
第1课时勾股定理
1.4 9 13 AC BC AB
2.解:(1)在直角三角形中,两条直角边的平方和等于斜边的平方.(2)证明:由图可知, .在直角三角形中,两条直角边的平方和等于斜边的平方.
3.10 4. D 5.8 6.(1)2 2 (2)2 2 7.
8.解:(1)∵在△ABC中,∠C=90°,b=2,c=3,∴a=√c -b = (2)设a=3x,则 解得x=8(负值舍去).∴3x=24,5x=40,即a=24,c=40.
9.4或 10. B 11. D 12. C 13.7 14. 15.169
16.解:∵CD⊥AB,∴∠ADC=∠BDC=90°.在 Rt△BCD中,BD= .设AC=AB=x,则AD=x--6.在Rt△ACD中, 即 解得
17. C
第2课时勾股定理的应用
1. D 2. C 3. C 4. C 5. B 6. D 7. C 8.21
9.解:这辆小汽车超速了,理由如下:在 Rt△ABC中,∠C=90°,AC=30m,AB=50 m,根据勾股定理,得 ∴小汽车的速度 ∴这辆小汽车超速了.
10. B11.8 12.85 13.7.5
14.解:(1)1.6 3 1 (2)∵BC⊥AC,∴∠ACB=90°.设秋千的长度为 xm,则AB=AD=xm,AC=AD--CD=(x--1)m.在Rt△ABC中,由勾股定理,得 即 x ,解得x=5.答:秋千的长度是5m .(3)4
15.5或8或
第3课时利用勾股定理作图
1. C 2.(-4,-1)
3.解:(1) (2)图略.
4. B5. C
6.解:图略.
7.(-3,3 8.2 -2 9.32 10.11 或25 11. B 12.<
13.
14.解:图略.
15.解:
