18.1.1 平行四边形的性质 分层练习(含答案)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 18.1.1 平行四边形的性质 分层练习(含答案)2024-2025学年人教版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 261.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 00:00:00 | ||
图片预览




文档简介
18.1.1 平行四边形的性质
第 1课时 平行四边形边、角的性质
A 基础题
知识点1 平行四边形的定义
1.(教材习题变式)如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形 ABCD,这个四边形是 .
2.如图,在 ABCD中,AB∥EG∥FH∥CD,则图中平行四边形的个数是 ( )
A.3 B.4 C.5 D.6
知识点2 平行四边形边、角的性质
3.(教材习题变式)在□ABCD中:
(1)若AB=3,AD=6,则它的周长为 .
(2)若 ABCD的周长为 32,且 AB=5,则BC= .
(3)若∠A=125°,则∠B= °,∠C= °,∠D= °.
(4)若∠A+∠C=140°,则∠A= °,∠B= °.
(5)若∠A:∠B=3:2,则∠A=∠C= °,∠B=∠D= °.
4.如图,在平行四边形ABCD 中,过点 C 作CE⊥AB,垂足为 E.若 ∠D = 50°, 则∠BCE 的度数为 .
5.(2023·株洲)如图所示,在 ABCD 中,AB=5,AD=3,∠DAB的平分线AE 交线段CD 于点E,则EC= .
6.(2023·凉山州)如图,□ABCO的顶点O,A,C的坐标分别是(0,0),(3,0),(1,2),则顶点B 的坐标是 .
7.(2024·湖北)如图,在 ABCD中,E,F为对角线 AC 上的两点,且 AE=CF,连接 BE,DF.求证:BE=DF.
知识点3 平行线间的距离
8.如图,a∥b,AB∥CD,CE⊥b,FG⊥b,垂足分别为E,G,则下列说法不正确的是 ( )
A. AB=CD
B. EC=GF
C. A,B两点间的距离就是线段AB 的长度
D. a与b 的距离就是线段CD 的长度
易错点 不注意分情况讨论,造成漏解
9.已知AB,CD,EF是同一平面内三条互相平行的直线,且 AB 与CD 的距离是 12 cm,EF与CD 的距离是5cm ,则AB与EF 的距离是 cm.
B 中档题
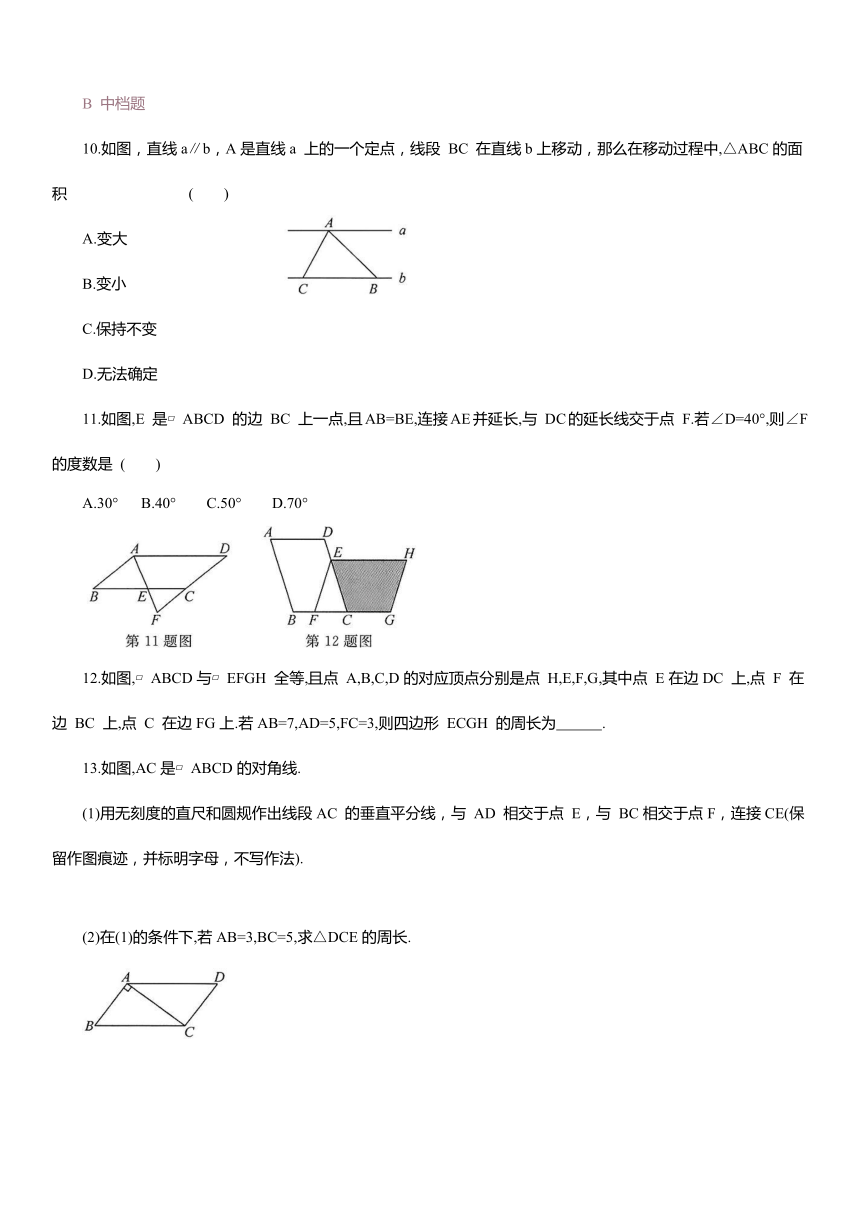
10.如图,直线a∥b,A是直线a 上的一个定点,线段 BC 在直线b上移动,那么在移动过程中,△ABC的面积 ( )
A.变大
B.变小
C.保持不变
D.无法确定
11.如图,E 是 ABCD 的边 BC 上一点,且AB=BE,连接AE并延长,与 DC的延长线交于点 F.若∠D=40°,则∠F的度数是 ( )
A.30° B.40° C.50° D.70°
12.如图, ABCD与 EFGH 全等,且点 A,B,C,D的对应顶点分别是点 H,E,F,G,其中点 E在边DC 上,点 F 在边 BC 上,点 C 在边FG上.若AB=7,AD=5,FC=3,则四边形 ECGH 的周长为 .
13.如图,AC是 ABCD的对角线.
(1)用无刻度的直尺和圆规作出线段AC 的垂直平分线,与 AD 相交于点 E,与 BC相交于点F,连接CE(保留作图痕迹,并标明字母,不写作法).
(2)在(1)的条件下,若AB=3,BC=5,求△DCE的周长.
14.如图,在 ABCD中,点 M 在边 AD 上,且AM=DM,CM,BA 的延长线相交于点E.
(1)求证:AE=AB.
(2)如果 BM平分∠ABC,求证:BM⊥CE.
微专题 2 平行四边形中“平行线+角平分线”基本图形的运用
【基本图形】 平行四边形+角平分线→等腰三角形,如:本课时T5,T14(2).
针对训练
1.(2024·南阳期末)如图,在 ABCD中,BF平分∠ABC交AD 于点F,CE平分∠BCD交AD 于点E.若BC=5,EF=1,则AB的长为( )
A.3 B.4 C.5 D.6
2.已知在 ABCD中,∠BAD的平分线把边 BC 分成长度分别是3和4 的两部分,则 ABCD的周长是 .
平行四边形对角线的性质
A 基础题
知识点1 平行四边形的对角线互相平分
1.(2023·益阳)如图,□ABCD的对角线AC,BD 相交于点O,则下列结论一定成立的是( )
A. OA=OB
B. OA⊥OB
C. OA=OC
D.∠OBA=∠OBC
2.如图,已知 ABCD的对角线AC,BD相交于点O,且 AC=8,BD=10,AB=5,则OA=OC= ,OB=OD= ,△OAB 的周长为 .
3.如图,在 ABCD中,对角线 AC,BD 相交于点O,AC=10,BD=12,则AB的取值范围为
4.如图,□ABCD的对角线AC与BD 相交于点O,AB⊥AC.若AB=3,BD=10,则AC的长是 .
5.如图,□ABCD 的对角线AC,BD 相交于点O,且AC+BD=36,AB=11,则△OCD的周长为 .
6.如图所示,在 ABCD中,对角线 AC与BD相交于点O,点 M,N在对角线 AC上,且 AM=CN.求证:BM∥DN.
知识点2 平行四边形的面积
7.如图, ABCD 的对角线相交于点 O.若S△AOD =2,则 S△AOB = ,S△BOC = ,S□ABCD= .
8.如图,在 ABCD中,AE⊥BC于点E,AF⊥DC于点F,BC=5,AB=4,AE=3,则AF的长为 .
9.如图,在 ABCD中,过点 D作DE⊥AB,垂足为 E,过点 B 作 BF⊥AC,垂足为 F.若AB=6,AC=10,DE=3,求 BF的长.
易错点 考虑不全面致错
10.如图,AC,BD是□ABCD的两条对角线,则图中的全等三角形共有 ( )
A.2对
B.3对
C.4对
D.6对
B 中档题
11.如图所示,在 ABCD中,EF过对角线AC,BD的交点O.若AB=4,BC=7,OE=3,则四边形 EFCD的周长是 ( )
A.14 B.11 C.17 D.10
【拓展设问1】 若四边形 EFCD 的面积为4,则 ABCD的面积为 .
【拓展设问2】 若△DOE 的面积为3,△COF的面积为2,则□ABCD的面积为 .
12.如图,在 ABCD中,对角线AC,BD相交于点O,过点 O作OE⊥AC交AD 于点 E.若AE=12,DE=5,AB=13,则 AC 的长为
13.如图,四边形 ABCD、四边形 ABDF 均为平行四边形,对角线 AC,BD相交于点O,BF,AD相交于点E.
(1)试猜想△BOC与△DEF 的面积关系,并说明理由.
(2)若AB=BC,求∠CAF 的度数.
C 综合题
14.如图,O为 ABCD 的对角线AC,BD的交点,∠BCO=90°,∠BOC=60°,BD=8,E 是OD 上的一动点,F是OB 上的一动点(点 E,F不与端点重合),且 DE=OF,连接 AE,CF.
(1)线段 EF 的长为 .
(2)若△OAE 的面积为 S ,△OCF 的面积为 的值是否发生变化 若不变,求出这个不变的值;若变化,请说明 的值是如何发生变化的.
微专题3 平行四边形中的面积问题模型
【模型归纳】 如本课时T11【拓展设问2】,T13(1),T14.
针对训练
1. 如图,E 是 ABCD内 任 意 一 点. 若 则图中阴影部分的面积是 .
2.如图,在□ABCD中,∠DAB 与∠CBA 的平分线相交于边 DC上的一点E.若AE=3,BE=2,则 ABCD的面积为
A.3 B.6 C.8 D.12
18.1.1 平行四边形的性质
第1课时 平行四边形边、角的性质
1.平行四边形2. D 3.(1)18 11 (2)55 125 55 (3)70 110(4)108 72 4.40° 5.2 6.(4,2)
7.证明:∵四边形 ABCD 是平行四边形,∴AB=CD,AB∥CD.∴∠BAE=∠DCF.在△BAE 和△DCF 中,
△BAE≌△DCF(SAS).∴BE=DF.
8. D 9.7或17 10. C 11. D 12.21
13.解:(1)图略.(2)∵四边形ABCD是平行四边形.∴CD=AB=3,AD=BC=5.∵EF是AC 的垂直平分线,∴AE=CE.∴△DCE的周长为CE+DE+CD=AE+DE+CD=AD+CD=5+3=8.
14.证明:(1)∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.
∴∠E=∠DCM.在△AEM和△DCM中, △AEM≌△DCM(AAS).∴AE=CD.∴AE=AB.(2)∵BM平分∠ABC,∴∠ABM=∠CBM.∵四边形ABCD 是平行四边形,∴AD∥BC,AD=BC.∴∠CBM=∠AMB.∴∠ABM=∠AMB.∴AB=AM.∵AB=AE,AM=DM,∴BE=2AB,BC=AD=2AM.∴BC=BE.∴△BCE是等腰三角形.∵BM平分∠ABC,∴BM⊥CE.
微专题2
1. A 2.22或20
第2课时 平行四边形对角线的性质
1. C 2.4 5 14 3.16.证明:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD.∵AM=CN,∴OM=ON.在△BOM 和△DON 中, ∴△BOM≌△DON(SAS).∴∠OBM=∠ODN.∴BM∥DN.
7.2 2 8 8.
9.解:∵四边形ABCD是平行四边形,∴S ABCD=2S△ABC.∴AB·DE=2× AC·BF.∴6×3=10BF.∴BF=
10. C 11. C 【拓展设问1】 8 【拓展设问2】 20 12.12
13.解: 理由如下:∵四边形 ABCD 是平行四边形, 同理, 又∵S ABCD=S ABDF .(2)∵四边形ABCD 是平行四边形,∴OA=OC.又∵AB=BC,∴AC⊥BD.∴∠COD=90°.∵四边形ABDF是平行四边形,∴AF∥BD.∴∠CAF=∠COD=90°.
14.解:(1)4 (2)S +S 的值不变.理由:连接AF.∵四边形ABCD是平行四边形,∴AO=OC.∴S△AOF =S△CDF.∵DE=OF,∴S△ADE=S△AOF=S△COF.∴S +S =S△AEF=S△AOD.∵四边形ABCD是平行四边形,∴AD∥BC,OD=OB.∴∠DAC=∠BCO=90°.∵∠AOD=∠BOC=60°,∴∠ADO=30°.∴AO= OD= BD=2.在 Rt△AOD中,
微专题3
1.4 2. B
第 1课时 平行四边形边、角的性质
A 基础题
知识点1 平行四边形的定义
1.(教材习题变式)如图,剪两张对边平行的纸条,随意交叉叠放在一起,转动其中的一张,重合的部分构成了一个四边形 ABCD,这个四边形是 .
2.如图,在 ABCD中,AB∥EG∥FH∥CD,则图中平行四边形的个数是 ( )
A.3 B.4 C.5 D.6
知识点2 平行四边形边、角的性质
3.(教材习题变式)在□ABCD中:
(1)若AB=3,AD=6,则它的周长为 .
(2)若 ABCD的周长为 32,且 AB=5,则BC= .
(3)若∠A=125°,则∠B= °,∠C= °,∠D= °.
(4)若∠A+∠C=140°,则∠A= °,∠B= °.
(5)若∠A:∠B=3:2,则∠A=∠C= °,∠B=∠D= °.
4.如图,在平行四边形ABCD 中,过点 C 作CE⊥AB,垂足为 E.若 ∠D = 50°, 则∠BCE 的度数为 .
5.(2023·株洲)如图所示,在 ABCD 中,AB=5,AD=3,∠DAB的平分线AE 交线段CD 于点E,则EC= .
6.(2023·凉山州)如图,□ABCO的顶点O,A,C的坐标分别是(0,0),(3,0),(1,2),则顶点B 的坐标是 .
7.(2024·湖北)如图,在 ABCD中,E,F为对角线 AC 上的两点,且 AE=CF,连接 BE,DF.求证:BE=DF.
知识点3 平行线间的距离
8.如图,a∥b,AB∥CD,CE⊥b,FG⊥b,垂足分别为E,G,则下列说法不正确的是 ( )
A. AB=CD
B. EC=GF
C. A,B两点间的距离就是线段AB 的长度
D. a与b 的距离就是线段CD 的长度
易错点 不注意分情况讨论,造成漏解
9.已知AB,CD,EF是同一平面内三条互相平行的直线,且 AB 与CD 的距离是 12 cm,EF与CD 的距离是5cm ,则AB与EF 的距离是 cm.
B 中档题
10.如图,直线a∥b,A是直线a 上的一个定点,线段 BC 在直线b上移动,那么在移动过程中,△ABC的面积 ( )
A.变大
B.变小
C.保持不变
D.无法确定
11.如图,E 是 ABCD 的边 BC 上一点,且AB=BE,连接AE并延长,与 DC的延长线交于点 F.若∠D=40°,则∠F的度数是 ( )
A.30° B.40° C.50° D.70°
12.如图, ABCD与 EFGH 全等,且点 A,B,C,D的对应顶点分别是点 H,E,F,G,其中点 E在边DC 上,点 F 在边 BC 上,点 C 在边FG上.若AB=7,AD=5,FC=3,则四边形 ECGH 的周长为 .
13.如图,AC是 ABCD的对角线.
(1)用无刻度的直尺和圆规作出线段AC 的垂直平分线,与 AD 相交于点 E,与 BC相交于点F,连接CE(保留作图痕迹,并标明字母,不写作法).
(2)在(1)的条件下,若AB=3,BC=5,求△DCE的周长.
14.如图,在 ABCD中,点 M 在边 AD 上,且AM=DM,CM,BA 的延长线相交于点E.
(1)求证:AE=AB.
(2)如果 BM平分∠ABC,求证:BM⊥CE.
微专题 2 平行四边形中“平行线+角平分线”基本图形的运用
【基本图形】 平行四边形+角平分线→等腰三角形,如:本课时T5,T14(2).
针对训练
1.(2024·南阳期末)如图,在 ABCD中,BF平分∠ABC交AD 于点F,CE平分∠BCD交AD 于点E.若BC=5,EF=1,则AB的长为( )
A.3 B.4 C.5 D.6
2.已知在 ABCD中,∠BAD的平分线把边 BC 分成长度分别是3和4 的两部分,则 ABCD的周长是 .
平行四边形对角线的性质
A 基础题
知识点1 平行四边形的对角线互相平分
1.(2023·益阳)如图,□ABCD的对角线AC,BD 相交于点O,则下列结论一定成立的是( )
A. OA=OB
B. OA⊥OB
C. OA=OC
D.∠OBA=∠OBC
2.如图,已知 ABCD的对角线AC,BD相交于点O,且 AC=8,BD=10,AB=5,则OA=OC= ,OB=OD= ,△OAB 的周长为 .
3.如图,在 ABCD中,对角线 AC,BD 相交于点O,AC=10,BD=12,则AB的取值范围为
4.如图,□ABCD的对角线AC与BD 相交于点O,AB⊥AC.若AB=3,BD=10,则AC的长是 .
5.如图,□ABCD 的对角线AC,BD 相交于点O,且AC+BD=36,AB=11,则△OCD的周长为 .
6.如图所示,在 ABCD中,对角线 AC与BD相交于点O,点 M,N在对角线 AC上,且 AM=CN.求证:BM∥DN.
知识点2 平行四边形的面积
7.如图, ABCD 的对角线相交于点 O.若S△AOD =2,则 S△AOB = ,S△BOC = ,S□ABCD= .
8.如图,在 ABCD中,AE⊥BC于点E,AF⊥DC于点F,BC=5,AB=4,AE=3,则AF的长为 .
9.如图,在 ABCD中,过点 D作DE⊥AB,垂足为 E,过点 B 作 BF⊥AC,垂足为 F.若AB=6,AC=10,DE=3,求 BF的长.
易错点 考虑不全面致错
10.如图,AC,BD是□ABCD的两条对角线,则图中的全等三角形共有 ( )
A.2对
B.3对
C.4对
D.6对
B 中档题
11.如图所示,在 ABCD中,EF过对角线AC,BD的交点O.若AB=4,BC=7,OE=3,则四边形 EFCD的周长是 ( )
A.14 B.11 C.17 D.10
【拓展设问1】 若四边形 EFCD 的面积为4,则 ABCD的面积为 .
【拓展设问2】 若△DOE 的面积为3,△COF的面积为2,则□ABCD的面积为 .
12.如图,在 ABCD中,对角线AC,BD相交于点O,过点 O作OE⊥AC交AD 于点 E.若AE=12,DE=5,AB=13,则 AC 的长为
13.如图,四边形 ABCD、四边形 ABDF 均为平行四边形,对角线 AC,BD相交于点O,BF,AD相交于点E.
(1)试猜想△BOC与△DEF 的面积关系,并说明理由.
(2)若AB=BC,求∠CAF 的度数.
C 综合题
14.如图,O为 ABCD 的对角线AC,BD的交点,∠BCO=90°,∠BOC=60°,BD=8,E 是OD 上的一动点,F是OB 上的一动点(点 E,F不与端点重合),且 DE=OF,连接 AE,CF.
(1)线段 EF 的长为 .
(2)若△OAE 的面积为 S ,△OCF 的面积为 的值是否发生变化 若不变,求出这个不变的值;若变化,请说明 的值是如何发生变化的.
微专题3 平行四边形中的面积问题模型
【模型归纳】 如本课时T11【拓展设问2】,T13(1),T14.
针对训练
1. 如图,E 是 ABCD内 任 意 一 点. 若 则图中阴影部分的面积是 .
2.如图,在□ABCD中,∠DAB 与∠CBA 的平分线相交于边 DC上的一点E.若AE=3,BE=2,则 ABCD的面积为
A.3 B.6 C.8 D.12
18.1.1 平行四边形的性质
第1课时 平行四边形边、角的性质
1.平行四边形2. D 3.(1)18 11 (2)55 125 55 (3)70 110(4)108 72 4.40° 5.2 6.(4,2)
7.证明:∵四边形 ABCD 是平行四边形,∴AB=CD,AB∥CD.∴∠BAE=∠DCF.在△BAE 和△DCF 中,
△BAE≌△DCF(SAS).∴BE=DF.
8. D 9.7或17 10. C 11. D 12.21
13.解:(1)图略.(2)∵四边形ABCD是平行四边形.∴CD=AB=3,AD=BC=5.∵EF是AC 的垂直平分线,∴AE=CE.∴△DCE的周长为CE+DE+CD=AE+DE+CD=AD+CD=5+3=8.
14.证明:(1)∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.
∴∠E=∠DCM.在△AEM和△DCM中, △AEM≌△DCM(AAS).∴AE=CD.∴AE=AB.(2)∵BM平分∠ABC,∴∠ABM=∠CBM.∵四边形ABCD 是平行四边形,∴AD∥BC,AD=BC.∴∠CBM=∠AMB.∴∠ABM=∠AMB.∴AB=AM.∵AB=AE,AM=DM,∴BE=2AB,BC=AD=2AM.∴BC=BE.∴△BCE是等腰三角形.∵BM平分∠ABC,∴BM⊥CE.
微专题2
1. A 2.22或20
第2课时 平行四边形对角线的性质
1. C 2.4 5 14 3.1
7.2 2 8 8.
9.解:∵四边形ABCD是平行四边形,∴S ABCD=2S△ABC.∴AB·DE=2× AC·BF.∴6×3=10BF.∴BF=
10. C 11. C 【拓展设问1】 8 【拓展设问2】 20 12.12
13.解: 理由如下:∵四边形 ABCD 是平行四边形, 同理, 又∵S ABCD=S ABDF .(2)∵四边形ABCD 是平行四边形,∴OA=OC.又∵AB=BC,∴AC⊥BD.∴∠COD=90°.∵四边形ABDF是平行四边形,∴AF∥BD.∴∠CAF=∠COD=90°.
14.解:(1)4 (2)S +S 的值不变.理由:连接AF.∵四边形ABCD是平行四边形,∴AO=OC.∴S△AOF =S△CDF.∵DE=OF,∴S△ADE=S△AOF=S△COF.∴S +S =S△AEF=S△AOD.∵四边形ABCD是平行四边形,∴AD∥BC,OD=OB.∴∠DAC=∠BCO=90°.∵∠AOD=∠BOC=60°,∴∠ADO=30°.∴AO= OD= BD=2.在 Rt△AOD中,
微专题3
1.4 2. B
