小专题8 与正方形有关的几个常考模型 同步练习(含答案)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 小专题8 与正方形有关的几个常考模型 同步练习(含答案)2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 167.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 07:52:14 | ||
图片预览

文档简介
小专题8 与正方形有关的几个常考模型
模型1 正方形中相交垂线段问题——教材P68复习题 T8 的变式与应用
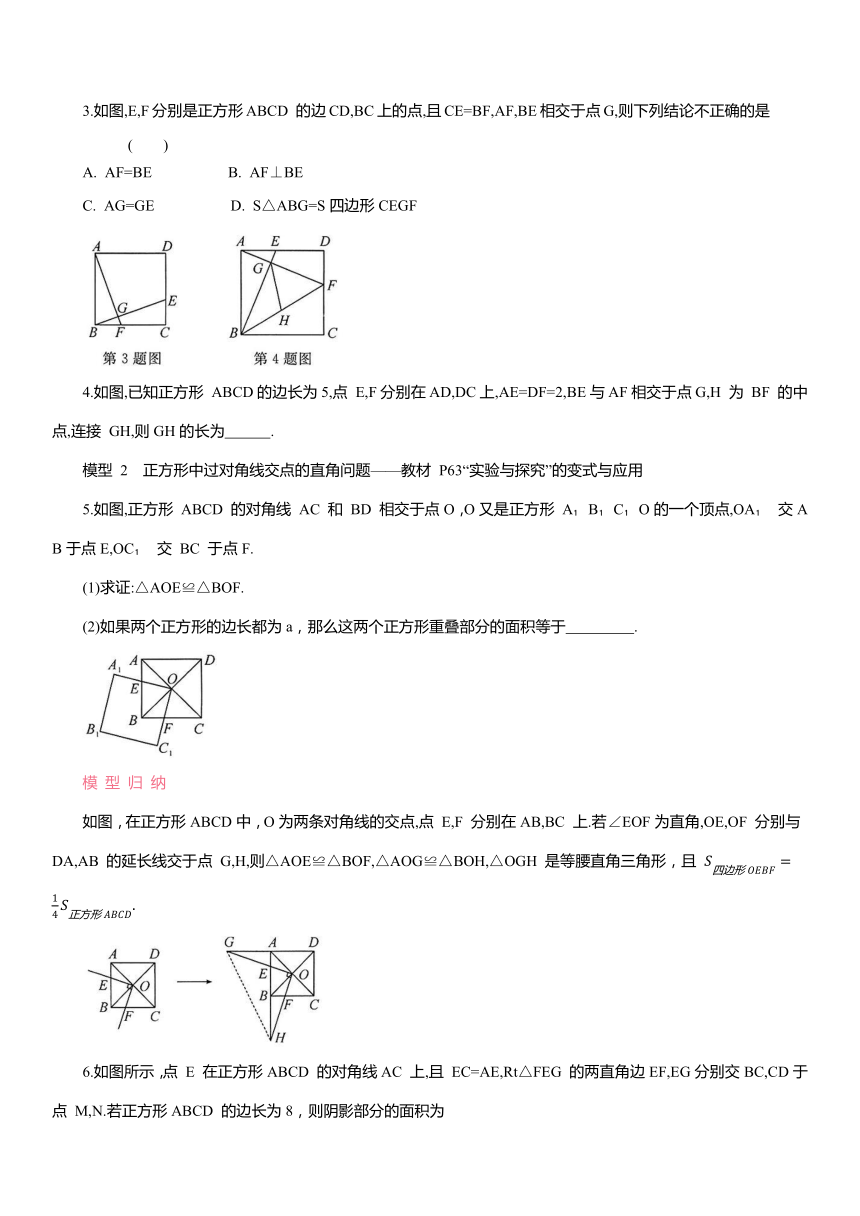
1.如图,ABCD 是一个正方形花园,E,F 是它的两个门,且 DE=CF.要修建两条路 BE 和AF,这两条路等长吗 它们有什么位置关系 为什么
2.(本专题 T1 变式)如图,在正方形ABCD中,点 E,F分别在边BC,CD上,AE,BF 相交于点O,∠AOF=90°.求证:BE=CF.
模 型 归 纳
分别连接正方形两组对边上的任意两点,得到的两条线段(如:图1中的线段 AF与 BE,图2 中的线段 AF 与EG,图3 中的线段 HF 与 EG,图4中的线段 AE 与 DF)满足:若垂直,则相等.
3.如图,E,F分别是正方形ABCD 的边CD,BC上的点,且CE=BF,AF,BE相交于点G,则下列结论不正确的是 ( )
A. AF=BE B. AF⊥BE
C. AG=GE D. S△ABG=S四边形CEGF
4.如图,已知正方形 ABCD的边长为5,点 E,F分别在AD,DC上,AE=DF=2,BE与AF相交于点G,H 为 BF 的中点,连接 GH,则GH的长为 .
模型 2 正方形中过对角线交点的直角问题——教材 P63“实验与探究”的变式与应用
5.如图,正方形 ABCD 的对角线 AC 和 BD 相交于点O,O又是正方形 A B C O的一个顶点,OA 交AB于点E,OC 交 BC 于点F.
(1)求证:△AOE≌△BOF.
(2)如果两个正方形的边长都为a,那么这两个正方形重叠部分的面积等于 .
模 型 归 纳
如图,在正方形ABCD中,O为两条对角线的交点,点 E,F 分别在AB,BC 上.若∠EOF为直角,OE,OF 分别与 DA,AB 的延长线交于点 G,H,则△AOE≌△BOF,△AOG≌△BOH,△OGH 是等腰直角三角形,且
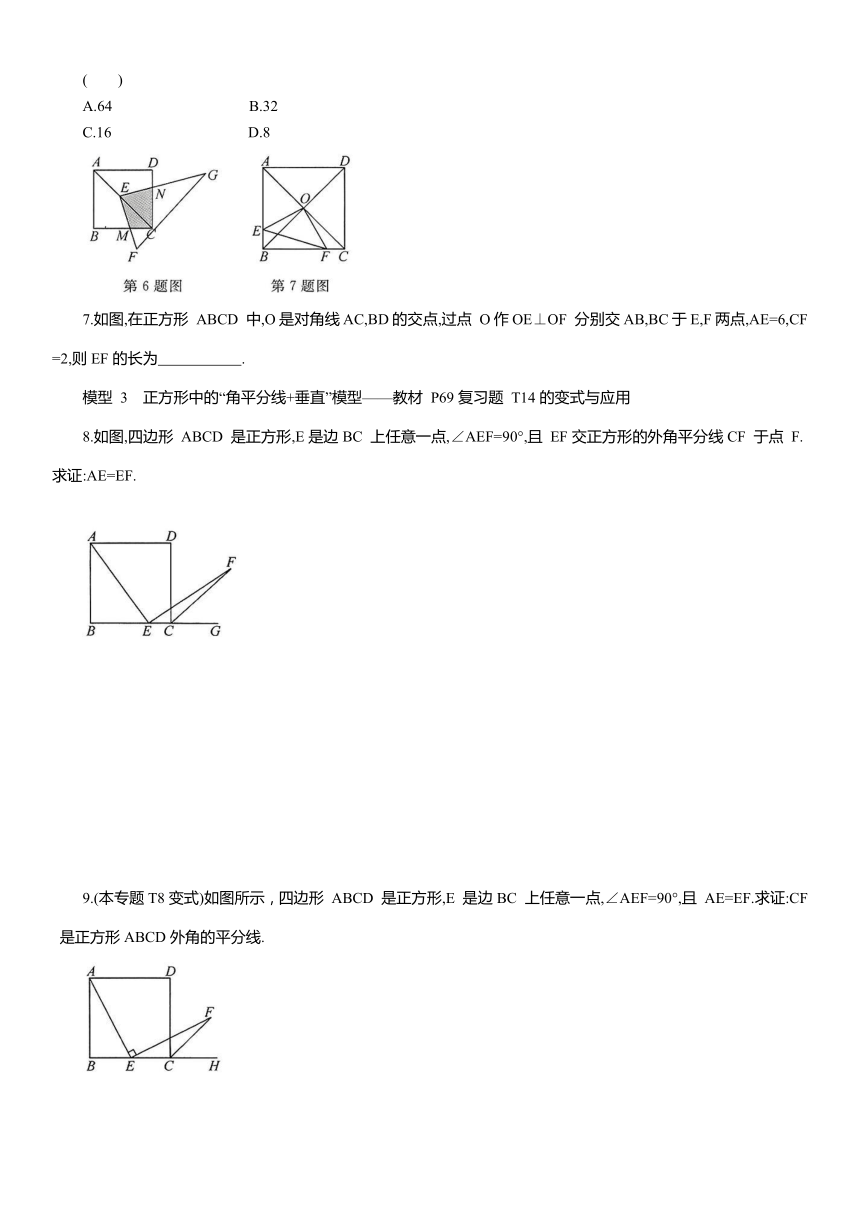
6.如图所示,点 E 在正方形ABCD 的对角线AC 上,且 EC=AE,Rt△FEG 的两直角边EF,EG分别交BC,CD于点 M,N.若正方形ABCD 的边长为8,则阴影部分的面积为
( )
A.64 B.32
C.16 D.8
7.如图,在正方形 ABCD 中,O是对角线AC,BD的交点,过点 O作OE⊥OF 分别交AB,BC于E,F两点,AE=6,CF=2,则EF的长为 .
模型 3 正方形中的“角平分线+垂直”模型——教材 P69复习题 T14的变式与应用
8.如图,四边形 ABCD 是正方形,E是边BC 上任意一点,∠AEF=90°,且 EF交正方形的外角平分线CF 于点 F.求证:AE=EF.
9.(本专题T8变式)如图所示,四边形 ABCD 是正方形,E 是边BC 上任意一点,∠AEF=90°,且 AE=EF.求证:CF 是正方形ABCD外角的平分线.
模 型 旧 纳
在正方形 ABCD 中,点 E 在射线 CB上,EF 交外角∠DCG 的平分线(图1)或其所在直线(图 2)于点 F,AE⊥EF,则有AE=EF.
10.如图,正方形ABCD的边长为1,E 是边BC上一动点(不与点 B,C重合),过点 E 作EF⊥AE,交正方形外角的平分线 CF 于点F,交 CD 于点 G,连接 AF.有下列结论:①AE AF=∠CEF.其中正确的是 (填序号).
模型4 正方形中的半角模型
11.如图,在正方形ABCD中,点E在BC上,点F在CD上,连接AE,AF,EF.若∠EAF=45°,BE=3,CF=4,求正方形ABCD的边长.
模 型 归 纳
(1)如图,在正方形 ABCD 中,若∠EAF=45°,则:
①EF=BE+DF;②△CEF 的周长为正方形 ABCD 边长的 2 倍;③FA 平分∠DFE,EA 平分∠BEF.
(2)如图,在正方形 ABCD 中,若∠EAF=45°,则 FA 平分∠DFE,EF =DF--BE.
12.如图,在正方形 ABCD 中,点 E,F 分别在BC,CD上,连接AE,AF,EF,∠EAF=45°.若∠BAE=α,则∠FEC= ( )
A.2α
小专题8 与正方形有关的几个常考模型
1.解:BE=AF且BE⊥AF.理由如下:∵四边形ABCD是正方形,∴
AB=AD=CD,∠BAE=∠D=90°.又∵DE=CF,∴AE=DF.∴△ABE≌△DAF(SAS).∴BE=AF,∠ABE=∠DAF.∵∠DAF+∠BAF=90°,∴∠ABE+∠BAF=90°.∴∠AGB=90°,即BE⊥AF.
2.证明:∵四边形ABCD是正方形,∴AB=BC,∠ABE=∠BCF=90°.∴∠CBF+∠OBA=90°.∵∠AOF=∠BAE+∠OBA=90°,∴∠BAE=∠CBF.∴△ABE≌△BCF(ASA).∴BE=CF.
5.解:(1)证明:∵在正方形ABCD中,AO=BO,∠AOB=∠A OC =90°,∠OAB=∠OBC=45°,∴∠AOE+∠EOB=90°,∠BOF+∠EOB = 90°. ∴ ∠AOE = ∠BOF. 在 △AOE 和△BOF 中, ∴△AOE≌△BOF(ASA).(2) a
6. C 7.2
8.证明:在AB上截取BM=BE,连接ME.∵∠B=90°,∴∠BME=∠BEM=45°.∵CF 平分∠DCG,∴∠FCG=45°.∴∠AME=∠ECF=135°.∵∠AEF=∠B=90°,∴∠AEB+∠CEF=∠AEB+∠MAE=90°.∴∠CEF=∠MAE.∵AB=BC,BM=BE,∴AM=EC.∴△AME≌△ECF(ASA).∴AE=EF.
9.证明:在AB上取一点G,使得AG=EC,连接GE.∵∠AEF=90°,∴∠AEB+∠CEF=90°.∵四边形 ABCD为正方形,∴AB=BC,∠B=90°.∴∠GAE+∠AEB=90°.∴∠GAE=∠CEF.又∵AE=EF,∴△AEG≌△EFC(SAS).∴∠AGE=∠ECF.∵AB=BC,AG=EC,∴BG=BE.∴∠BGE=45°.∴∠ECF=∠AGE=135°.∴∠DCF=∠FCH=45°.∴CF是正方形ABCD 外角的平分线.
10.①②
11.解:延长CB至点G,使BG=DF,连接AG.∵四边形ABCD是正方形,∴AB=AD,∠ABE=∠D=∠BAD=90°.∴∠ABG=∠ABE=∠D=90°.∴△ABG≌△ADF(SAS). ∴AG=AF,∠BAG=∠DAF.∵∠DAF+∠BAE=90°-45°=45°,∴∠BAG+∠BAE=∠EAG=45°.∴∠EAG=∠EAF.又∵AE=AE,∴△AEG≌△AEF(SAS).∴EF=EG=BE+BG=BE+DF.设正方形ABCD的边长为x,则CE=x-3,DF=x-4.∴EF=BE+DF=x-1.在 Rt△CEF中, (x-1) .∴x=6.∴正方形ABCD的边长为6.12. A
模型1 正方形中相交垂线段问题——教材P68复习题 T8 的变式与应用
1.如图,ABCD 是一个正方形花园,E,F 是它的两个门,且 DE=CF.要修建两条路 BE 和AF,这两条路等长吗 它们有什么位置关系 为什么
2.(本专题 T1 变式)如图,在正方形ABCD中,点 E,F分别在边BC,CD上,AE,BF 相交于点O,∠AOF=90°.求证:BE=CF.
模 型 归 纳
分别连接正方形两组对边上的任意两点,得到的两条线段(如:图1中的线段 AF与 BE,图2 中的线段 AF 与EG,图3 中的线段 HF 与 EG,图4中的线段 AE 与 DF)满足:若垂直,则相等.
3.如图,E,F分别是正方形ABCD 的边CD,BC上的点,且CE=BF,AF,BE相交于点G,则下列结论不正确的是 ( )
A. AF=BE B. AF⊥BE
C. AG=GE D. S△ABG=S四边形CEGF
4.如图,已知正方形 ABCD的边长为5,点 E,F分别在AD,DC上,AE=DF=2,BE与AF相交于点G,H 为 BF 的中点,连接 GH,则GH的长为 .
模型 2 正方形中过对角线交点的直角问题——教材 P63“实验与探究”的变式与应用
5.如图,正方形 ABCD 的对角线 AC 和 BD 相交于点O,O又是正方形 A B C O的一个顶点,OA 交AB于点E,OC 交 BC 于点F.
(1)求证:△AOE≌△BOF.
(2)如果两个正方形的边长都为a,那么这两个正方形重叠部分的面积等于 .
模 型 归 纳
如图,在正方形ABCD中,O为两条对角线的交点,点 E,F 分别在AB,BC 上.若∠EOF为直角,OE,OF 分别与 DA,AB 的延长线交于点 G,H,则△AOE≌△BOF,△AOG≌△BOH,△OGH 是等腰直角三角形,且
6.如图所示,点 E 在正方形ABCD 的对角线AC 上,且 EC=AE,Rt△FEG 的两直角边EF,EG分别交BC,CD于点 M,N.若正方形ABCD 的边长为8,则阴影部分的面积为
( )
A.64 B.32
C.16 D.8
7.如图,在正方形 ABCD 中,O是对角线AC,BD的交点,过点 O作OE⊥OF 分别交AB,BC于E,F两点,AE=6,CF=2,则EF的长为 .
模型 3 正方形中的“角平分线+垂直”模型——教材 P69复习题 T14的变式与应用
8.如图,四边形 ABCD 是正方形,E是边BC 上任意一点,∠AEF=90°,且 EF交正方形的外角平分线CF 于点 F.求证:AE=EF.
9.(本专题T8变式)如图所示,四边形 ABCD 是正方形,E 是边BC 上任意一点,∠AEF=90°,且 AE=EF.求证:CF 是正方形ABCD外角的平分线.
模 型 旧 纳
在正方形 ABCD 中,点 E 在射线 CB上,EF 交外角∠DCG 的平分线(图1)或其所在直线(图 2)于点 F,AE⊥EF,则有AE=EF.
10.如图,正方形ABCD的边长为1,E 是边BC上一动点(不与点 B,C重合),过点 E 作EF⊥AE,交正方形外角的平分线 CF 于点F,交 CD 于点 G,连接 AF.有下列结论:①AE AF=∠CEF.其中正确的是 (填序号).
模型4 正方形中的半角模型
11.如图,在正方形ABCD中,点E在BC上,点F在CD上,连接AE,AF,EF.若∠EAF=45°,BE=3,CF=4,求正方形ABCD的边长.
模 型 归 纳
(1)如图,在正方形 ABCD 中,若∠EAF=45°,则:
①EF=BE+DF;②△CEF 的周长为正方形 ABCD 边长的 2 倍;③FA 平分∠DFE,EA 平分∠BEF.
(2)如图,在正方形 ABCD 中,若∠EAF=45°,则 FA 平分∠DFE,EF =DF--BE.
12.如图,在正方形 ABCD 中,点 E,F 分别在BC,CD上,连接AE,AF,EF,∠EAF=45°.若∠BAE=α,则∠FEC= ( )
A.2α
小专题8 与正方形有关的几个常考模型
1.解:BE=AF且BE⊥AF.理由如下:∵四边形ABCD是正方形,∴
AB=AD=CD,∠BAE=∠D=90°.又∵DE=CF,∴AE=DF.∴△ABE≌△DAF(SAS).∴BE=AF,∠ABE=∠DAF.∵∠DAF+∠BAF=90°,∴∠ABE+∠BAF=90°.∴∠AGB=90°,即BE⊥AF.
2.证明:∵四边形ABCD是正方形,∴AB=BC,∠ABE=∠BCF=90°.∴∠CBF+∠OBA=90°.∵∠AOF=∠BAE+∠OBA=90°,∴∠BAE=∠CBF.∴△ABE≌△BCF(ASA).∴BE=CF.
5.解:(1)证明:∵在正方形ABCD中,AO=BO,∠AOB=∠A OC =90°,∠OAB=∠OBC=45°,∴∠AOE+∠EOB=90°,∠BOF+∠EOB = 90°. ∴ ∠AOE = ∠BOF. 在 △AOE 和△BOF 中, ∴△AOE≌△BOF(ASA).(2) a
6. C 7.2
8.证明:在AB上截取BM=BE,连接ME.∵∠B=90°,∴∠BME=∠BEM=45°.∵CF 平分∠DCG,∴∠FCG=45°.∴∠AME=∠ECF=135°.∵∠AEF=∠B=90°,∴∠AEB+∠CEF=∠AEB+∠MAE=90°.∴∠CEF=∠MAE.∵AB=BC,BM=BE,∴AM=EC.∴△AME≌△ECF(ASA).∴AE=EF.
9.证明:在AB上取一点G,使得AG=EC,连接GE.∵∠AEF=90°,∴∠AEB+∠CEF=90°.∵四边形 ABCD为正方形,∴AB=BC,∠B=90°.∴∠GAE+∠AEB=90°.∴∠GAE=∠CEF.又∵AE=EF,∴△AEG≌△EFC(SAS).∴∠AGE=∠ECF.∵AB=BC,AG=EC,∴BG=BE.∴∠BGE=45°.∴∠ECF=∠AGE=135°.∴∠DCF=∠FCH=45°.∴CF是正方形ABCD 外角的平分线.
10.①②
11.解:延长CB至点G,使BG=DF,连接AG.∵四边形ABCD是正方形,∴AB=AD,∠ABE=∠D=∠BAD=90°.∴∠ABG=∠ABE=∠D=90°.∴△ABG≌△ADF(SAS). ∴AG=AF,∠BAG=∠DAF.∵∠DAF+∠BAE=90°-45°=45°,∴∠BAG+∠BAE=∠EAG=45°.∴∠EAG=∠EAF.又∵AE=AE,∴△AEG≌△AEF(SAS).∴EF=EG=BE+BG=BE+DF.设正方形ABCD的边长为x,则CE=x-3,DF=x-4.∴EF=BE+DF=x-1.在 Rt△CEF中, (x-1) .∴x=6.∴正方形ABCD的边长为6.12. A
