18.2.2菱形 分层练习(含答案)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 18.2.2菱形 分层练习(含答案)2024-2025学年人教版八年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 228.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 07:54:05 | ||
图片预览



文档简介
18.2.2菱形
菱形的性质
A 基础题
知识点1 菱形的性质
1.关于菱形的性质,以下说法不正确的是( )
A.四条边相等 B.对角线相等
C.对角线互相垂直 D.是轴对称图形
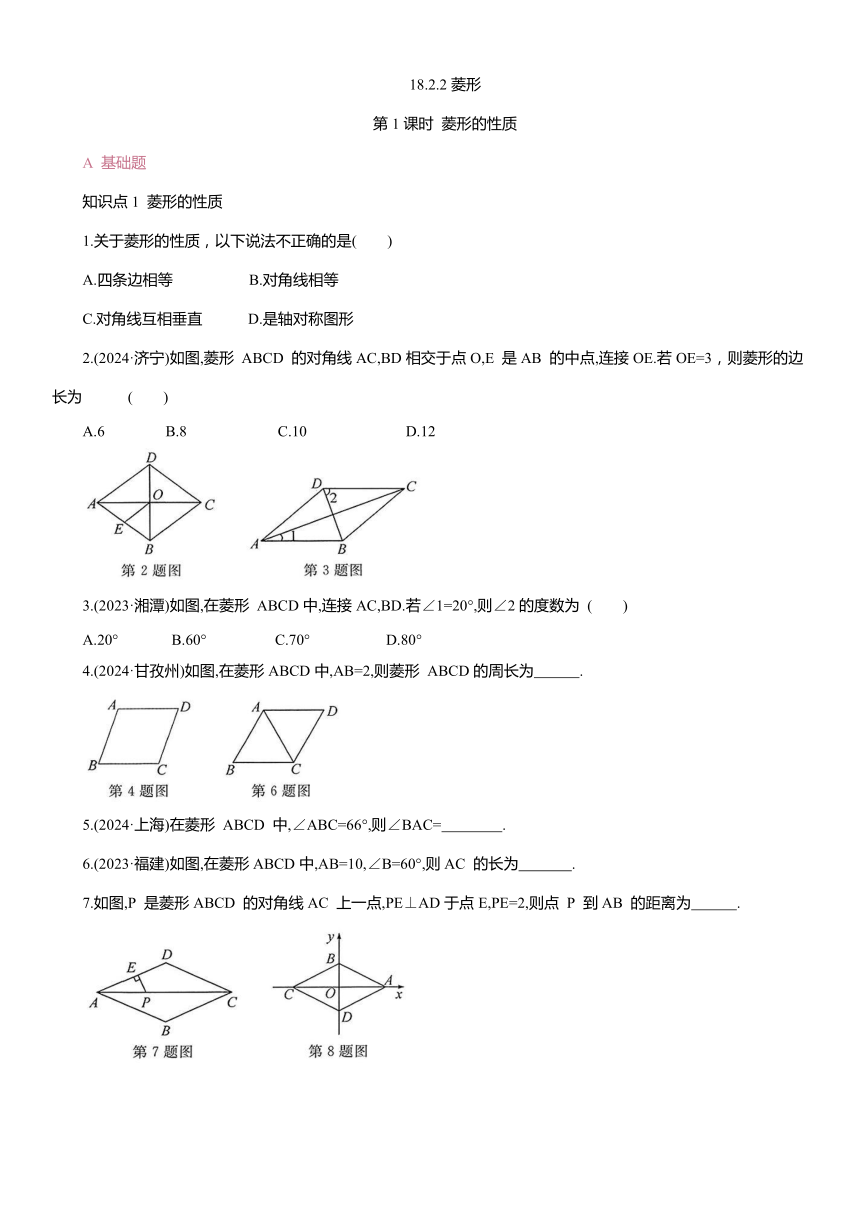
2.(2024·济宁)如图,菱形 ABCD 的对角线AC,BD相交于点O,E 是AB 的中点,连接OE.若OE=3,则菱形的边长为 ( )
A.6 B.8 C.10 D.12
3.(2023·湘潭)如图,在菱形 ABCD中,连接AC,BD.若∠1=20°,则∠2的度数为 ( )
A.20° B.60° C.70° D.80°
4.(2024·甘孜州)如图,在菱形ABCD中,AB=2,则菱形 ABCD的周长为 .
5.(2024·上海)在菱形 ABCD 中,∠ABC=66°,则∠BAC= .
6.(2023·福建)如图,在菱形ABCD中,AB=10,∠B=60°,则AC 的长为 .
7.如图,P 是菱形ABCD 的对角线AC 上一点,PE⊥AD于点E,PE=2,则点 P 到AB 的距离为 .
8.如图,在平面直角坐标系中,菱形ABCD对角线的交点坐标是O(0,0),点 B 的坐标是(0,1),且 则点 A 的坐标是 .
9.(2024·福建)如图,在菱形ABCD中,点 E,F分别在边 BC和CD 上,且∠AEB=∠AFD.求证:BE=DF.
知识点2 菱形的面积
10.(2023·临沂)若菱形的两条对角线长分别为6和8,则该菱形的面积为 .
11.(教材习题变式)如图,四边形ABCD是菱形,对角线 AC,BD相交于点 O,且∠ACD=30°,BD=4,求菱形ABCD的面积.
B 中档题
12.(2024·临夏州)如图,O是坐标原点,菱形ABOC 的顶点 B 在x轴的负半轴上,顶点 C的坐标为(3,4),则顶点 A 的坐标为 ( )
A.(-4,2)
C.(-2,4)
13.(2024·绥化)如图,四边形 ABCD 是菱形,CD=5,BD=8,AE⊥BC于点 E,则AE的长是 ( )
A.
14.(2023 · 绍兴)如图,在菱形 ABCD 中,∠DAB=40°,连接AC,以点 A 为圆心,AC的长为半径作弧,交直线 AD 于点 E,连接CE,则∠AEC的度数是 .
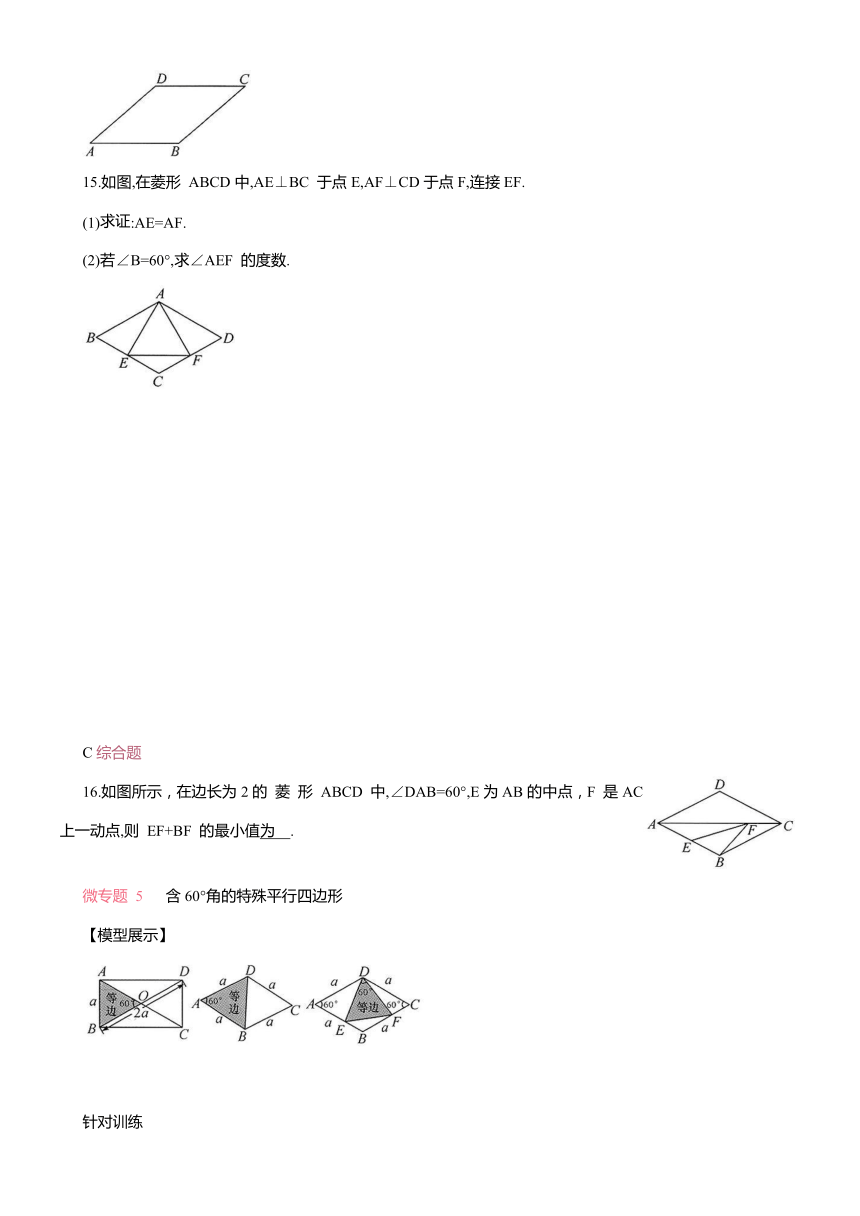
15.如图,在菱形 ABCD中,AE⊥BC 于点E,AF⊥CD于点F,连接EF.
(1)求证:AE=AF.
(2)若∠B=60°,求∠AEF 的度数.
C综合题
16.如图所示,在边长为2的 菱 形 ABCD 中,∠DAB=60°,E为AB的中点,F 是AC 上一动点,则 EF+BF 的最小值为 .
微专题 5 含60°角的特殊平行四边形
【模型展示】
针对训练
1.如图,在矩形 ABCD 中,对角线 AC,BD 相交于点O,DE 平分∠ADC. 若E∠AOB=60°,则∠COE= °.
2.(本课时 T15 变式)如图,在菱形ABCD中,∠A=60°,AB=3,E,F分别为AD,DC上的动点,∠EBF=60°,点 E 从点 A 向点 D运动的过程中,AE+CF 的长度 ( )
A.逐渐减小
B.恒等于3
C.先减小再增加
D.恒大于3
第2课时 菱形的判定
A基础题
知识点1 有一组邻边相等的平行四边形是菱形
1.如图,四边形 ABCD 的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形 ABCD为菱形的是 ( )
A. AD=CD
B. AB=AD
C. AC=BD
D.∠BAC=∠BCA
2.如图,在 ABCD中,BE平分∠ABC 交AD于点E,点 F 在 BC上,AB=BF,连接AF 交BE 于点O,连接 EF.求证:四边形 ABFE 是菱形.
知识点2 对角线互相垂直的平行四边形是菱形
3. 新考向 开放性问题(2023·齐齐哈尔)如图,在四边形 ABCD中,AD=BC,AC⊥BD 于点O.请添加一个条件: ,使四边形 ABCD为菱形.
4.(2023·永州)如图,已知四边形ABCD 是平行四边形,其对角线相交于点 O,OA=3,BD=8,AB=5.
(1)△AOB 是直角三角形吗 请说明理由.
(2)求证:四边形 ABCD 是菱形.
知识点3 四条边相等的四边形是菱形
5.(2024·自贡)如图,以点 A 为圆心,适当的长为半径画弧,分别交∠A的两边于点M,N;再分别以点 M,N为圆心,AM 的长为半径画弧,两弧交于点 B,连接 MB,NB.若∠A=40°,则∠MBN= ( )
A.40°
B.50°
C.60°
D.140°
6.如图,已知在四边形ABCD中,AB=AD,BD平分∠ABC,∠A=∠C.求证:四边形ABCD为菱形.
B 中档题
7.(2023·深圳)如图,在□ABCD中,AB=4,BC=6,将线段AB水平向右平移a 个单位长度得到线段EF.要使四边形 ECDF 为菱形,则a的值为 ( )
A.1 B.2 C.3 D.4
8.用尺规在一个平行四边形内作菱形 ABCD,下列作法中,错误的是 ( )
9.(教材习题变式)(2024·广西)如图,两张宽度均为3c m的纸条交叉叠放在一起,交叉形成的锐角为 60°,则重合部分构成的四边形ABCD的周长为 cm.
10.如图,在△ABC中,∠BCA=90°,CD 是边AB 上的中线,分别过点 C,D 作 BA 和BC的平行线,两线交于点 E,且DE交AC 于点O,连接AE.
(1)求证:四边形 ADCE是菱形.
(2)若∠B=60°,BC=6,求四边形 ADCE 的面积.
C综合题
11.综合与实践:
(1)如图1,在平行四边形纸片 ABCD中,AD=5,S□ABCD =15,过点 A 作 AE⊥BC,垂足为E,沿 AE 剪下△ABE,将它平移至 △DCE'的位置,拼成四边形AEE'D,则四边形 AEE'D 的形状为
(2)如图2,在(1)中的四边形纸片AEE'D 的边 EE'上取一点 F,使 EF=4,剪下△AEF,将它平移至△DE'F'的位置,拼成四边形 AFF'D.
①求证:四边形 AFF'D 是菱形.
②求四边形AFF'D的两条对角线的长.
18.2.2 菱形
第1 课时 菱形的性质
1. B 2. A 3. C 4.8 5.57° 6.10 7.2 8.(2,0)
9.证明:∵四边形ABCD是菱形,∴AB=AD,∠B=∠D.在△ABE和△ADF 中,∠AEEBDE∠AFD,∴△ABE≌△ADF(AAS).∴BE=DF.
10.24
11.解:∵四边形 ABCD 是菱形, ∵在Rt△OCD中,∠OCD=30°,∴CD
12. C 13. A 14.10°或80°
15.解:(1)证明:∵四边形 ABCD是菱形,∴AB=AD,∠B=∠D.∵AE⊥BC,AF⊥CD,∴∠AEB=∠AFD=90°.在△ABE 和△ADF
中,AAER-D∠AFD,∴△ABE≌△ADF(AAS).∴AE=AF.
(2)∵四边形ABCD是菱形,∴BC∥AD.∴∠B+∠BAD=180°.∵∠B=60°,∴∠BAD=120°. ∵∠AEB=90°,∠B=60°,∴∠BAE=30°.由(1)得,△ABE≌△ADF,∴∠BAE=∠DAF= .又∵AE=AF,∴△AEF 是等边三角形.∴∠AEF=60°.
16.
微专题5
1.75 2. B
第2课时 菱形的判定
1. C
2.证明:∵四边形 ABCD 是平行四边形,∴AD∥BC.∴∠AEB=∠FBE.∵ BE 平分∠ABC,∴∠ABE =∠FBE. ∴∠AEB=∠ABE.∴AE=AB.∵BF=AB,∴AE=BF.∴四边形ABFE是平行四边形.∵AB=BF,∴平行四边形ABFE是菱形.
3. AD∥BC(答案不唯一)
4.解:(1)△AOB是直角三角形.理由如下:∵四边形 ABCD是平行四边形, OA +OB =AB .∴△AOB是直角三角形,且∠AOB=90°.(2)证明:由(1)知,∠AOB=90°,∴AC⊥BD.∴平行四边形 ABCD是菱形.
5. A
6.证明:∵BD平分∠ABC,∴∠ABD=∠CBD.在△ABD和△CBD
中,(∠A==∠C,BD,∵ ∴△ABD≌△CBD(AAS).∴AB=BC,AD
=DC.∵AB=AD,∴AB=BC=DC=AD.∴四边形ABCD是菱形.
7. B 8. C 9.8
10.解:(1)证明:∵DE∥BC,EC∥AB,∴四边形 DBCE是平行四边形.∴且EC=DB.在Rt△ABC中,CD为边AB上的中线,∴AD=DB=CD.∴EC=AD.∴四边形ADCE 是平行四边形.又∵AD=CD,∴平行四边形ADCE是菱形.(2)在Rt△ABC中,CD 为边AB上的中线,∠B=60°,BC=6,∴AB=2BC=12.在 Rt△ABC中,由勾股定理,得 ∵四边形 DBCE 是平行四边形,
11.解:(1)矩形 (2)①证明:∵AF∥DF',AF=DF',∴四边形 AFF'D是平行四边形.∵AD=5,S矩形AEE'D=S□ABCD=15,∴AE=3.又∵EF=4,∴在 Rt△AEF 中, 5.∴平行四边形 AFF'D 是菱形.②连接AF',DF.在 Rt△DE'F中,∵E'F=E'E-EF=5-4=1,DE'=3,∴DF=√E'D +E'F 在Rt△AEF'中,
菱形的性质
A 基础题
知识点1 菱形的性质
1.关于菱形的性质,以下说法不正确的是( )
A.四条边相等 B.对角线相等
C.对角线互相垂直 D.是轴对称图形
2.(2024·济宁)如图,菱形 ABCD 的对角线AC,BD相交于点O,E 是AB 的中点,连接OE.若OE=3,则菱形的边长为 ( )
A.6 B.8 C.10 D.12
3.(2023·湘潭)如图,在菱形 ABCD中,连接AC,BD.若∠1=20°,则∠2的度数为 ( )
A.20° B.60° C.70° D.80°
4.(2024·甘孜州)如图,在菱形ABCD中,AB=2,则菱形 ABCD的周长为 .
5.(2024·上海)在菱形 ABCD 中,∠ABC=66°,则∠BAC= .
6.(2023·福建)如图,在菱形ABCD中,AB=10,∠B=60°,则AC 的长为 .
7.如图,P 是菱形ABCD 的对角线AC 上一点,PE⊥AD于点E,PE=2,则点 P 到AB 的距离为 .
8.如图,在平面直角坐标系中,菱形ABCD对角线的交点坐标是O(0,0),点 B 的坐标是(0,1),且 则点 A 的坐标是 .
9.(2024·福建)如图,在菱形ABCD中,点 E,F分别在边 BC和CD 上,且∠AEB=∠AFD.求证:BE=DF.
知识点2 菱形的面积
10.(2023·临沂)若菱形的两条对角线长分别为6和8,则该菱形的面积为 .
11.(教材习题变式)如图,四边形ABCD是菱形,对角线 AC,BD相交于点 O,且∠ACD=30°,BD=4,求菱形ABCD的面积.
B 中档题
12.(2024·临夏州)如图,O是坐标原点,菱形ABOC 的顶点 B 在x轴的负半轴上,顶点 C的坐标为(3,4),则顶点 A 的坐标为 ( )
A.(-4,2)
C.(-2,4)
13.(2024·绥化)如图,四边形 ABCD 是菱形,CD=5,BD=8,AE⊥BC于点 E,则AE的长是 ( )
A.
14.(2023 · 绍兴)如图,在菱形 ABCD 中,∠DAB=40°,连接AC,以点 A 为圆心,AC的长为半径作弧,交直线 AD 于点 E,连接CE,则∠AEC的度数是 .
15.如图,在菱形 ABCD中,AE⊥BC 于点E,AF⊥CD于点F,连接EF.
(1)求证:AE=AF.
(2)若∠B=60°,求∠AEF 的度数.
C综合题
16.如图所示,在边长为2的 菱 形 ABCD 中,∠DAB=60°,E为AB的中点,F 是AC 上一动点,则 EF+BF 的最小值为 .
微专题 5 含60°角的特殊平行四边形
【模型展示】
针对训练
1.如图,在矩形 ABCD 中,对角线 AC,BD 相交于点O,DE 平分∠ADC. 若E∠AOB=60°,则∠COE= °.
2.(本课时 T15 变式)如图,在菱形ABCD中,∠A=60°,AB=3,E,F分别为AD,DC上的动点,∠EBF=60°,点 E 从点 A 向点 D运动的过程中,AE+CF 的长度 ( )
A.逐渐减小
B.恒等于3
C.先减小再增加
D.恒大于3
第2课时 菱形的判定
A基础题
知识点1 有一组邻边相等的平行四边形是菱形
1.如图,四边形 ABCD 的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形 ABCD为菱形的是 ( )
A. AD=CD
B. AB=AD
C. AC=BD
D.∠BAC=∠BCA
2.如图,在 ABCD中,BE平分∠ABC 交AD于点E,点 F 在 BC上,AB=BF,连接AF 交BE 于点O,连接 EF.求证:四边形 ABFE 是菱形.
知识点2 对角线互相垂直的平行四边形是菱形
3. 新考向 开放性问题(2023·齐齐哈尔)如图,在四边形 ABCD中,AD=BC,AC⊥BD 于点O.请添加一个条件: ,使四边形 ABCD为菱形.
4.(2023·永州)如图,已知四边形ABCD 是平行四边形,其对角线相交于点 O,OA=3,BD=8,AB=5.
(1)△AOB 是直角三角形吗 请说明理由.
(2)求证:四边形 ABCD 是菱形.
知识点3 四条边相等的四边形是菱形
5.(2024·自贡)如图,以点 A 为圆心,适当的长为半径画弧,分别交∠A的两边于点M,N;再分别以点 M,N为圆心,AM 的长为半径画弧,两弧交于点 B,连接 MB,NB.若∠A=40°,则∠MBN= ( )
A.40°
B.50°
C.60°
D.140°
6.如图,已知在四边形ABCD中,AB=AD,BD平分∠ABC,∠A=∠C.求证:四边形ABCD为菱形.
B 中档题
7.(2023·深圳)如图,在□ABCD中,AB=4,BC=6,将线段AB水平向右平移a 个单位长度得到线段EF.要使四边形 ECDF 为菱形,则a的值为 ( )
A.1 B.2 C.3 D.4
8.用尺规在一个平行四边形内作菱形 ABCD,下列作法中,错误的是 ( )
9.(教材习题变式)(2024·广西)如图,两张宽度均为3c m的纸条交叉叠放在一起,交叉形成的锐角为 60°,则重合部分构成的四边形ABCD的周长为 cm.
10.如图,在△ABC中,∠BCA=90°,CD 是边AB 上的中线,分别过点 C,D 作 BA 和BC的平行线,两线交于点 E,且DE交AC 于点O,连接AE.
(1)求证:四边形 ADCE是菱形.
(2)若∠B=60°,BC=6,求四边形 ADCE 的面积.
C综合题
11.综合与实践:
(1)如图1,在平行四边形纸片 ABCD中,AD=5,S□ABCD =15,过点 A 作 AE⊥BC,垂足为E,沿 AE 剪下△ABE,将它平移至 △DCE'的位置,拼成四边形AEE'D,则四边形 AEE'D 的形状为
(2)如图2,在(1)中的四边形纸片AEE'D 的边 EE'上取一点 F,使 EF=4,剪下△AEF,将它平移至△DE'F'的位置,拼成四边形 AFF'D.
①求证:四边形 AFF'D 是菱形.
②求四边形AFF'D的两条对角线的长.
18.2.2 菱形
第1 课时 菱形的性质
1. B 2. A 3. C 4.8 5.57° 6.10 7.2 8.(2,0)
9.证明:∵四边形ABCD是菱形,∴AB=AD,∠B=∠D.在△ABE和△ADF 中,∠AEEBDE∠AFD,∴△ABE≌△ADF(AAS).∴BE=DF.
10.24
11.解:∵四边形 ABCD 是菱形, ∵在Rt△OCD中,∠OCD=30°,∴CD
12. C 13. A 14.10°或80°
15.解:(1)证明:∵四边形 ABCD是菱形,∴AB=AD,∠B=∠D.∵AE⊥BC,AF⊥CD,∴∠AEB=∠AFD=90°.在△ABE 和△ADF
中,AAER-D∠AFD,∴△ABE≌△ADF(AAS).∴AE=AF.
(2)∵四边形ABCD是菱形,∴BC∥AD.∴∠B+∠BAD=180°.∵∠B=60°,∴∠BAD=120°. ∵∠AEB=90°,∠B=60°,∴∠BAE=30°.由(1)得,△ABE≌△ADF,∴∠BAE=∠DAF= .又∵AE=AF,∴△AEF 是等边三角形.∴∠AEF=60°.
16.
微专题5
1.75 2. B
第2课时 菱形的判定
1. C
2.证明:∵四边形 ABCD 是平行四边形,∴AD∥BC.∴∠AEB=∠FBE.∵ BE 平分∠ABC,∴∠ABE =∠FBE. ∴∠AEB=∠ABE.∴AE=AB.∵BF=AB,∴AE=BF.∴四边形ABFE是平行四边形.∵AB=BF,∴平行四边形ABFE是菱形.
3. AD∥BC(答案不唯一)
4.解:(1)△AOB是直角三角形.理由如下:∵四边形 ABCD是平行四边形, OA +OB =AB .∴△AOB是直角三角形,且∠AOB=90°.(2)证明:由(1)知,∠AOB=90°,∴AC⊥BD.∴平行四边形 ABCD是菱形.
5. A
6.证明:∵BD平分∠ABC,∴∠ABD=∠CBD.在△ABD和△CBD
中,(∠A==∠C,BD,∵ ∴△ABD≌△CBD(AAS).∴AB=BC,AD
=DC.∵AB=AD,∴AB=BC=DC=AD.∴四边形ABCD是菱形.
7. B 8. C 9.8
10.解:(1)证明:∵DE∥BC,EC∥AB,∴四边形 DBCE是平行四边形.∴且EC=DB.在Rt△ABC中,CD为边AB上的中线,∴AD=DB=CD.∴EC=AD.∴四边形ADCE 是平行四边形.又∵AD=CD,∴平行四边形ADCE是菱形.(2)在Rt△ABC中,CD 为边AB上的中线,∠B=60°,BC=6,∴AB=2BC=12.在 Rt△ABC中,由勾股定理,得 ∵四边形 DBCE 是平行四边形,
11.解:(1)矩形 (2)①证明:∵AF∥DF',AF=DF',∴四边形 AFF'D是平行四边形.∵AD=5,S矩形AEE'D=S□ABCD=15,∴AE=3.又∵EF=4,∴在 Rt△AEF 中, 5.∴平行四边形 AFF'D 是菱形.②连接AF',DF.在 Rt△DE'F中,∵E'F=E'E-EF=5-4=1,DE'=3,∴DF=√E'D +E'F 在Rt△AEF'中,
