18.2.1 矩形 分层练习(含答案)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 18.2.1 矩形 分层练习(含答案)2024-2025学年人教版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 192.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 00:00:00 | ||
图片预览


文档简介
18.2.1 矩形
第 1课时 矩形的性质
A基础题
知识点1 矩形边、角的性质
1.下列性质中,矩形ABCD 不一定具有的是( )
A. AB=BC B. AB∥CD
C.∠ABC=90° D. AB=CD
2.(2024·辽宁)如图,在矩形ABCD中,点E在AD上,当△EBC是等边三角形时,∠AEB=( )
A.30°
B.45°
C.60°
D.120°
3.已知矩形的一边长为6 cm,一条对角线的长为 10 cm,则矩形的面积为 cm .
4.(2024·陕西)如图,四边形 ABCD 是矩形,点E 和点 F 在边 BC 上,且 BE=CF.求证:AF=DE.
知识点2 矩形的对角线相等
5.(2024·成都)如图,在矩形 ABCD中,对角线AC 与BD 相交于点O,则下列结论一定正确的是 ( )
A. AB=AD
B. AC⊥BD
C. AC=BD
D.∠ACB=∠ACD
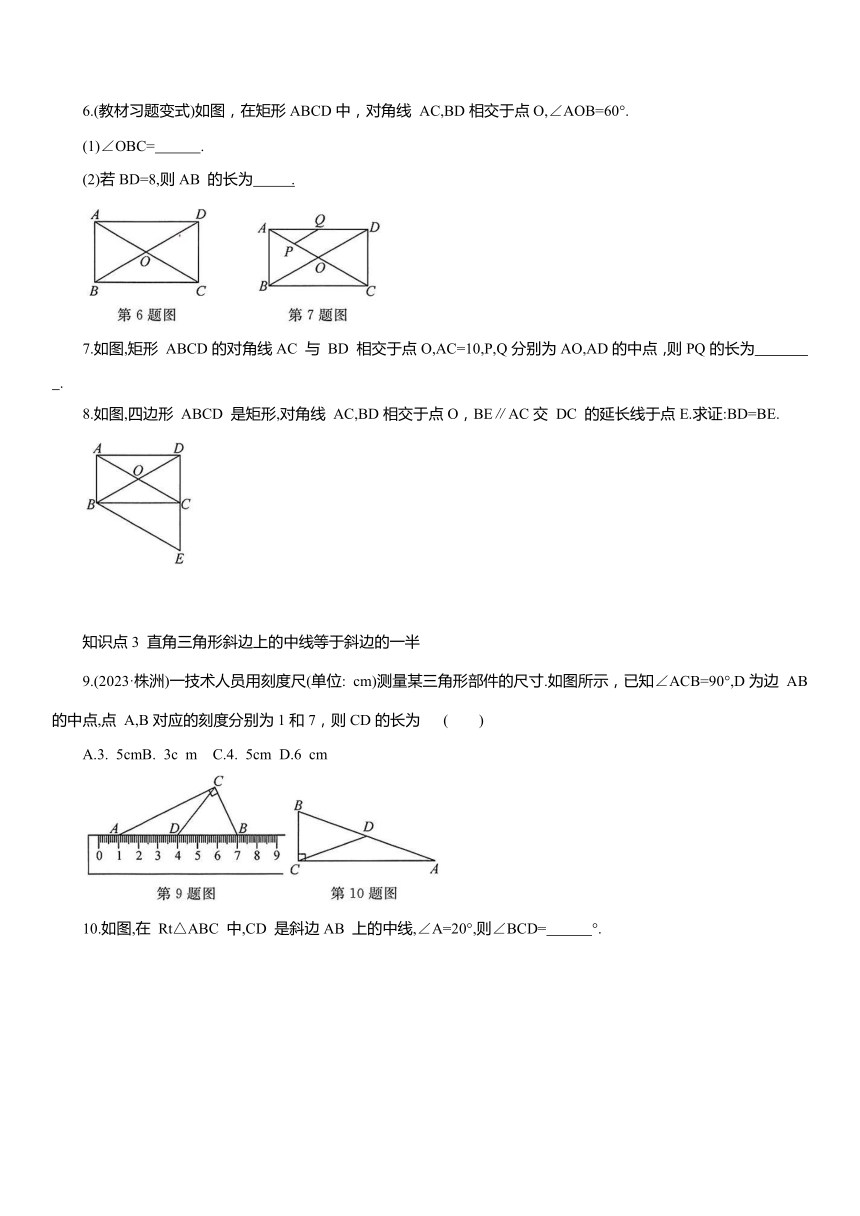
6.(教材习题变式)如图,在矩形ABCD中,对角线 AC,BD相交于点O,∠AOB=60°.
(1)∠OBC= .
(2)若BD=8,则AB 的长为 .
7.如图,矩形 ABCD的对角线AC 与 BD 相交于点O,AC=10,P,Q分别为AO,AD的中点,则PQ的长为 .
8.如图,四边形 ABCD 是矩形,对角线 AC,BD相交于点O,BE∥AC交 DC 的延长线于点E.求证:BD=BE.
知识点3 直角三角形斜边上的中线等于斜边的一半
9.(2023·株洲)一技术人员用刻度尺(单位: cm)测量某三角形部件的尺寸.如图所示,已知∠ACB=90°,D为边 AB的中点,点 A,B对应的刻度分别为1和7,则CD的长为 ( )
A.3. 5cmB. 3c m C.4. 5cm D.6 cm
10.如图,在 Rt△ABC 中,CD 是斜边AB 上的中线,∠A=20°,则∠BCD= °.
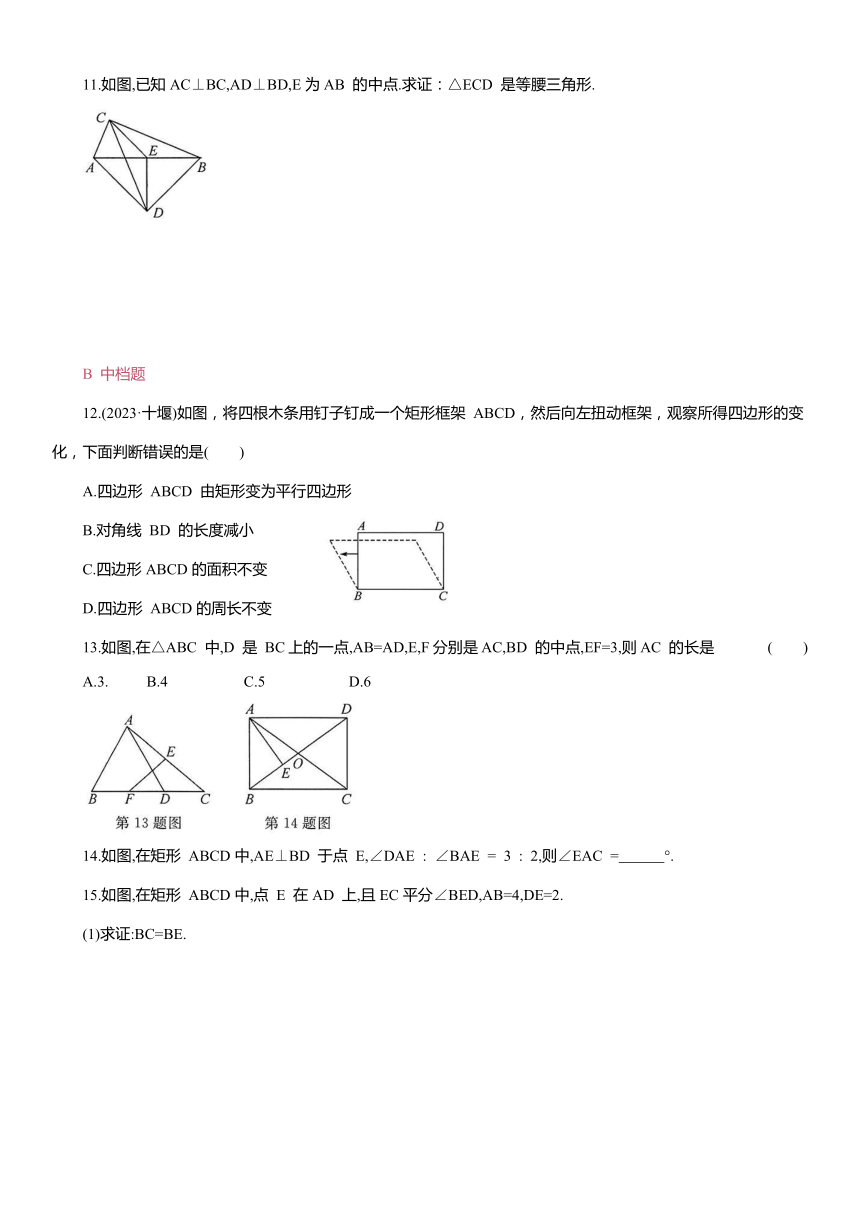
11.如图,已知AC⊥BC,AD⊥BD,E为AB 的中点.求证:△ECD 是等腰三角形.
B 中档题
12.(2023·十堰)如图,将四根木条用钉子钉成一个矩形框架 ABCD,然后向左扭动框架,观察所得四边形的变化,下面判断错误的是( )
A.四边形 ABCD 由矩形变为平行四边形
B.对角线 BD 的长度减小
C.四边形ABCD的面积不变
D.四边形 ABCD的周长不变
13.如图,在△ABC 中,D 是 BC上的一点,AB=AD,E,F分别是AC,BD 的中点,EF=3,则AC 的长是 ( )
A.3. B.4 C.5 D.6
14.如图,在矩形 ABCD中,AE⊥BD 于点 E,∠DAE : ∠BAE = 3 : 2,则∠EAC = °.
15.如图,在矩形 ABCD中,点 E 在AD 上,且EC平分∠BED,AB=4,DE=2.
(1)求证:BC=BE.
(2)求△BEC的面积.
16.如图,在矩形ABCD中,AC是对角线.
(1)实践与操作:作线段 AC的垂直平分线,垂足为O,交边 AD 于点 E,交边 BC于点F(要求:尺规作图,保留作图痕迹,不写作法,标明字母).
(2)猜想与证明:试猜想线段 AE 与CF 的数量关系,并加以证明.
C综合题
17.在矩形ABCD中,M是对角线BD 上一点,AB=3,BC=4.当△AMD为等腰三角形时,BM 的长为 .
第 2课时 矩形的判定
A 基础题
知识点1 有一个角是直角的平行四边形是矩形
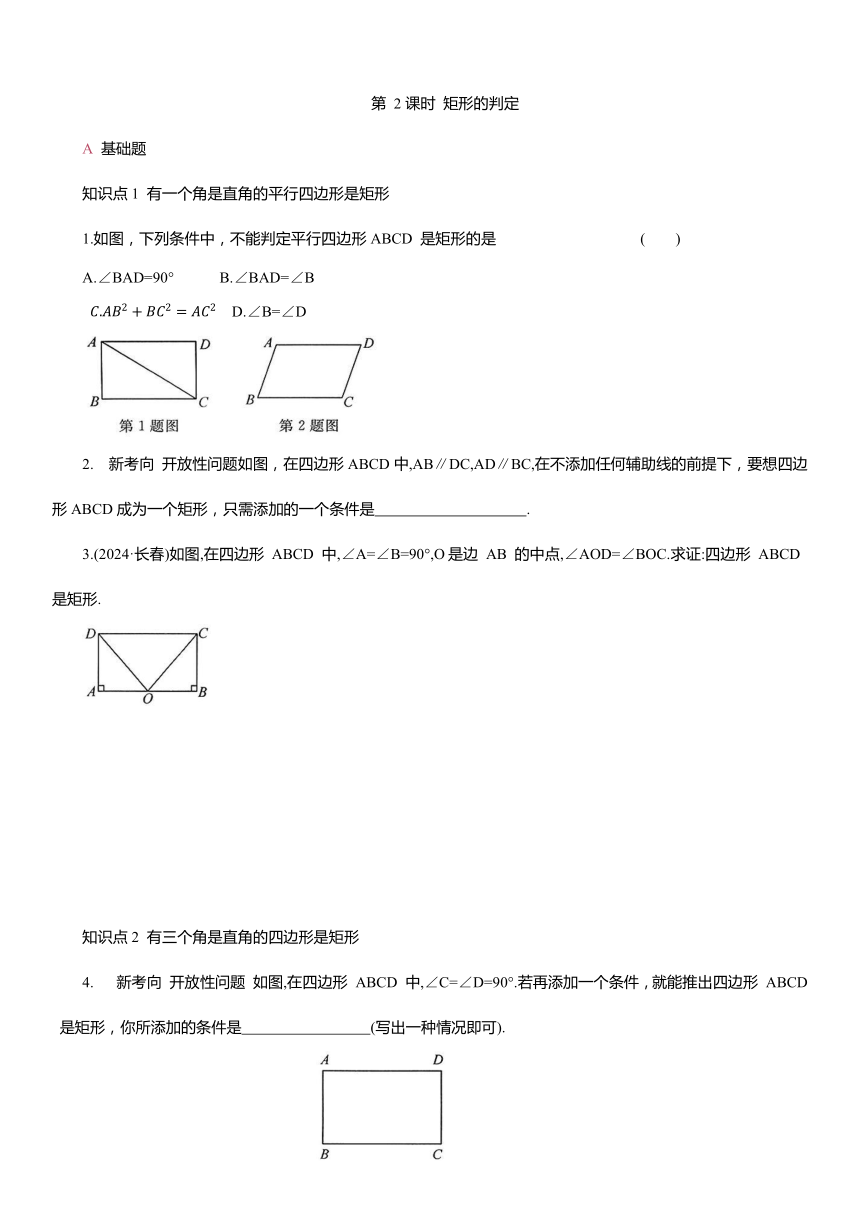
1.如图,下列条件中,不能判定平行四边形ABCD 是矩形的是 ( )
A.∠BAD=90° B.∠BAD=∠B
D.∠B=∠D
2. 新考向 开放性问题如图,在四边形ABCD中,AB∥DC,AD∥BC,在不添加任何辅助线的前提下,要想四边形ABCD成为一个矩形,只需添加的一个条件是 .
3.(2024·长春)如图,在四边形 ABCD 中,∠A=∠B=90°,O是边 AB 的中点,∠AOD=∠BOC.求证:四边形 ABCD 是矩形.
知识点2 有三个角是直角的四边形是矩形
4. 新考向 开放性问题 如图,在四边形 ABCD 中,∠C=∠D=90°.若再添加一个条件,就能推出四边形 ABCD 是矩形,你所添加的条件是 (写出一种情况即可).
5.如图,在△ABC中,AB=AC,AE⊥BC,AD平分∠FAC,CD⊥AD 于点 D.求证:四边形AECD 是矩形.
知识点3 对角线相等的平行四边形是矩形
6.要检验一个四边形的桌面是否为矩形,可行的测量方案是 ( )
A.测量两条对角线是否相等
B.度量两个角是不是90°
C.测量两条对角线的交点到四个顶点的距离是否相等
D.测量两组对边是否分别相等
7.(2023·北京节选)如图,在 ABCD 中,点E,F分别在BC,AD上,BE=DF,AC=EF.求证:四边形AECF 是矩形.
易错点 对矩形的判定方法理解错误导致出错
8.下列命题正确的是 ( )
A.有一个角是直角的平行四边形是矩形
B.四条边相等的四边形是矩形
C.有一组邻边相等的平行四边形是矩形
D.对角线相等的四边形是矩形
B 中档题
9.依据所标数据,下列四边形不一定为矩形的是 ( )
10.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,E,F,G,H 分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形 EFGH 的面积为 .
11.如图,在 Rt△ABC中,∠BAC=90°,且 AB=5,AC=12,P是斜边BC上的一个动点,过点 P分别作 PM⊥AC于点M,PN⊥AB 于点 N,连接 MN,则线段 MN的最小值为 .
12.(2024·兰州)如图,在△ABC中,AB=AC,D是BC 的中点,CE∥AD,AE⊥AD,EF⊥AC.
(1)求证:四边形ADCE 是矩形.
(2)若 BC=4,CE=3,求 EF的长.
C 综合题
13.如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙、无重叠的四边形EFGH.
(1)求证:四边形 EFGH 是矩形.
(2)若EH=3cm,EF=4 cm,求边 AD的长.
18.2.1 矩形
第1 课时 矩形的性质
1. A 2. C 3.48
4.证明:∵四边形ABCD为矩形,∴AB=CD,∠B=∠C=90°.∵BE=CF,∴BE+EF=CF+EF,即BF=CE.在△ABF和△DCE中,
AB=CC,∴△ABF≌△DCE(SASC.在△ABFDE,
5. C 6.(1)30° (2)4 7.2.5
8.证明:∵四边形ABCD是矩形,∴AC=BD,AB∥CD.又∵BE∥AC,∴四边形ABEC是平行四边形.∴AC=BE.∴BD=BE.
9. B 10.70
11.证明:∵AC⊥BC,AD⊥BD,∴∠ACB=∠ADB=90°.又∵E为AB 的中点 是等腰三角形.
12. C 13. D 14.18
15.解:(1)证明:∵四边形 ABCD 是矩形,∴AD∥BC,∠A=90°,AB=CD=4.∴∠DEC=∠ECB.∵EC平分∠BED,∴∠BEC=∠DEC.∴∠BEC=∠ECB.∴BC=BE.(2)设 BC=BE=x,则
16.解:(1)图略.(2)AE=CF.证明如下:∵四边形 ABCD是矩形,∴AD∥BC.∴∠EAO=∠FCO,∠AEO=∠CFO.∵EF是AC 的垂直平分线,∴AO=CO.在△AOE 和△COF 中, ∴△AOE≌△COF(AAS).∴AE=CF.
17. 或1
第2 课时 矩形的判定
1. D 2.∠A=90°(答案不唯一)
3.证明:∵O是边AB 的中点,∴OA=OB.在△AOD 和△BOC中,
(0024-00-2-8)∴△AOD≌△BOC(ASA).∴DA=CB.∵∠A
=∠B=90°,∴∠A+∠B=180°.∴DA∥CB.∴四边形ABCD是平行四边形.又∵∠A=90°,∴平行四边形ABCD是矩形.
4.∠A=90°(答案不唯一)
5.证明:∵AB=AC,AE⊥BC,∴∠AEC=90°,∠BAE=∠CAE= ∠BAC.∵AD平分∠FAC,∴∠DAC= ∠FAC.∴∠DAE= 又∵CD⊥AD,∴∠ADC=90°.∴四边形AECD是矩形.
6. C
7.证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC.∵BE=DF,∴AD-DF=BC-BE,即AF=EC.∴四边形AECF是平行四边形.又∵AC=EF,∴平行四边形 AECF 是矩形.
8. A 9. D 10.12 11.
12.解:(1)证明:∵AB=AC,D是BC 的中点,∴AD⊥BC,即∠ADC=∠ADB=90°.∵CE∥AD,∴∠ECD=∠ADB=90°.∵AE⊥AD,∴∠EAD=90°.∴∠ADC=∠ECD=∠EAD=90°.∴四边形ADCE是矩形.(2)∵D是BC 的中点, =2.由(1)可知,四边形ADCE是矩形,∴AE=CD=2,∠AEC=90°.在 Rt△AEC中,AE=2,CE=3,由勾股定理,得 AC=√AE +CE = .∵EF⊥AC,∴S△AEC= AC·EF= AE
13.解:(1)证明:由折叠的性质,得∠HEJ=∠AEH,∠BEF=∠FEJ,∴∠HEF=∠HEJ+∠FEJ= ×180°=90°.同理可得,∠EHG=∠HGF=∠EFG=90°,∴四边形 EFGH 是矩形. 5(cm).由折叠的性质,得 = CD,HD=HK,CF=KF,∴AE=CG.∵四边形EFGH是矩形,∴EH=GF.又∵∠A=∠C=90°,∴Rt△AEH≌Rt△CGF(HL).∴AH=CF.∴AH=KF.∴AD=AH+HD=FK+HK=HF=5cm.
第 1课时 矩形的性质
A基础题
知识点1 矩形边、角的性质
1.下列性质中,矩形ABCD 不一定具有的是( )
A. AB=BC B. AB∥CD
C.∠ABC=90° D. AB=CD
2.(2024·辽宁)如图,在矩形ABCD中,点E在AD上,当△EBC是等边三角形时,∠AEB=( )
A.30°
B.45°
C.60°
D.120°
3.已知矩形的一边长为6 cm,一条对角线的长为 10 cm,则矩形的面积为 cm .
4.(2024·陕西)如图,四边形 ABCD 是矩形,点E 和点 F 在边 BC 上,且 BE=CF.求证:AF=DE.
知识点2 矩形的对角线相等
5.(2024·成都)如图,在矩形 ABCD中,对角线AC 与BD 相交于点O,则下列结论一定正确的是 ( )
A. AB=AD
B. AC⊥BD
C. AC=BD
D.∠ACB=∠ACD
6.(教材习题变式)如图,在矩形ABCD中,对角线 AC,BD相交于点O,∠AOB=60°.
(1)∠OBC= .
(2)若BD=8,则AB 的长为 .
7.如图,矩形 ABCD的对角线AC 与 BD 相交于点O,AC=10,P,Q分别为AO,AD的中点,则PQ的长为 .
8.如图,四边形 ABCD 是矩形,对角线 AC,BD相交于点O,BE∥AC交 DC 的延长线于点E.求证:BD=BE.
知识点3 直角三角形斜边上的中线等于斜边的一半
9.(2023·株洲)一技术人员用刻度尺(单位: cm)测量某三角形部件的尺寸.如图所示,已知∠ACB=90°,D为边 AB的中点,点 A,B对应的刻度分别为1和7,则CD的长为 ( )
A.3. 5cmB. 3c m C.4. 5cm D.6 cm
10.如图,在 Rt△ABC 中,CD 是斜边AB 上的中线,∠A=20°,则∠BCD= °.
11.如图,已知AC⊥BC,AD⊥BD,E为AB 的中点.求证:△ECD 是等腰三角形.
B 中档题
12.(2023·十堰)如图,将四根木条用钉子钉成一个矩形框架 ABCD,然后向左扭动框架,观察所得四边形的变化,下面判断错误的是( )
A.四边形 ABCD 由矩形变为平行四边形
B.对角线 BD 的长度减小
C.四边形ABCD的面积不变
D.四边形 ABCD的周长不变
13.如图,在△ABC 中,D 是 BC上的一点,AB=AD,E,F分别是AC,BD 的中点,EF=3,则AC 的长是 ( )
A.3. B.4 C.5 D.6
14.如图,在矩形 ABCD中,AE⊥BD 于点 E,∠DAE : ∠BAE = 3 : 2,则∠EAC = °.
15.如图,在矩形 ABCD中,点 E 在AD 上,且EC平分∠BED,AB=4,DE=2.
(1)求证:BC=BE.
(2)求△BEC的面积.
16.如图,在矩形ABCD中,AC是对角线.
(1)实践与操作:作线段 AC的垂直平分线,垂足为O,交边 AD 于点 E,交边 BC于点F(要求:尺规作图,保留作图痕迹,不写作法,标明字母).
(2)猜想与证明:试猜想线段 AE 与CF 的数量关系,并加以证明.
C综合题
17.在矩形ABCD中,M是对角线BD 上一点,AB=3,BC=4.当△AMD为等腰三角形时,BM 的长为 .
第 2课时 矩形的判定
A 基础题
知识点1 有一个角是直角的平行四边形是矩形
1.如图,下列条件中,不能判定平行四边形ABCD 是矩形的是 ( )
A.∠BAD=90° B.∠BAD=∠B
D.∠B=∠D
2. 新考向 开放性问题如图,在四边形ABCD中,AB∥DC,AD∥BC,在不添加任何辅助线的前提下,要想四边形ABCD成为一个矩形,只需添加的一个条件是 .
3.(2024·长春)如图,在四边形 ABCD 中,∠A=∠B=90°,O是边 AB 的中点,∠AOD=∠BOC.求证:四边形 ABCD 是矩形.
知识点2 有三个角是直角的四边形是矩形
4. 新考向 开放性问题 如图,在四边形 ABCD 中,∠C=∠D=90°.若再添加一个条件,就能推出四边形 ABCD 是矩形,你所添加的条件是 (写出一种情况即可).
5.如图,在△ABC中,AB=AC,AE⊥BC,AD平分∠FAC,CD⊥AD 于点 D.求证:四边形AECD 是矩形.
知识点3 对角线相等的平行四边形是矩形
6.要检验一个四边形的桌面是否为矩形,可行的测量方案是 ( )
A.测量两条对角线是否相等
B.度量两个角是不是90°
C.测量两条对角线的交点到四个顶点的距离是否相等
D.测量两组对边是否分别相等
7.(2023·北京节选)如图,在 ABCD 中,点E,F分别在BC,AD上,BE=DF,AC=EF.求证:四边形AECF 是矩形.
易错点 对矩形的判定方法理解错误导致出错
8.下列命题正确的是 ( )
A.有一个角是直角的平行四边形是矩形
B.四条边相等的四边形是矩形
C.有一组邻边相等的平行四边形是矩形
D.对角线相等的四边形是矩形
B 中档题
9.依据所标数据,下列四边形不一定为矩形的是 ( )
10.如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,E,F,G,H 分别为边AD,AB,BC,CD的中点.若AC=8,BD=6,则四边形 EFGH 的面积为 .
11.如图,在 Rt△ABC中,∠BAC=90°,且 AB=5,AC=12,P是斜边BC上的一个动点,过点 P分别作 PM⊥AC于点M,PN⊥AB 于点 N,连接 MN,则线段 MN的最小值为 .
12.(2024·兰州)如图,在△ABC中,AB=AC,D是BC 的中点,CE∥AD,AE⊥AD,EF⊥AC.
(1)求证:四边形ADCE 是矩形.
(2)若 BC=4,CE=3,求 EF的长.
C 综合题
13.如图,将矩形纸片ABCD的四个角向内折起,恰好拼成一个无缝隙、无重叠的四边形EFGH.
(1)求证:四边形 EFGH 是矩形.
(2)若EH=3cm,EF=4 cm,求边 AD的长.
18.2.1 矩形
第1 课时 矩形的性质
1. A 2. C 3.48
4.证明:∵四边形ABCD为矩形,∴AB=CD,∠B=∠C=90°.∵BE=CF,∴BE+EF=CF+EF,即BF=CE.在△ABF和△DCE中,
AB=CC,∴△ABF≌△DCE(SASC.在△ABFDE,
5. C 6.(1)30° (2)4 7.2.5
8.证明:∵四边形ABCD是矩形,∴AC=BD,AB∥CD.又∵BE∥AC,∴四边形ABEC是平行四边形.∴AC=BE.∴BD=BE.
9. B 10.70
11.证明:∵AC⊥BC,AD⊥BD,∴∠ACB=∠ADB=90°.又∵E为AB 的中点 是等腰三角形.
12. C 13. D 14.18
15.解:(1)证明:∵四边形 ABCD 是矩形,∴AD∥BC,∠A=90°,AB=CD=4.∴∠DEC=∠ECB.∵EC平分∠BED,∴∠BEC=∠DEC.∴∠BEC=∠ECB.∴BC=BE.(2)设 BC=BE=x,则
16.解:(1)图略.(2)AE=CF.证明如下:∵四边形 ABCD是矩形,∴AD∥BC.∴∠EAO=∠FCO,∠AEO=∠CFO.∵EF是AC 的垂直平分线,∴AO=CO.在△AOE 和△COF 中, ∴△AOE≌△COF(AAS).∴AE=CF.
17. 或1
第2 课时 矩形的判定
1. D 2.∠A=90°(答案不唯一)
3.证明:∵O是边AB 的中点,∴OA=OB.在△AOD 和△BOC中,
(0024-00-2-8)∴△AOD≌△BOC(ASA).∴DA=CB.∵∠A
=∠B=90°,∴∠A+∠B=180°.∴DA∥CB.∴四边形ABCD是平行四边形.又∵∠A=90°,∴平行四边形ABCD是矩形.
4.∠A=90°(答案不唯一)
5.证明:∵AB=AC,AE⊥BC,∴∠AEC=90°,∠BAE=∠CAE= ∠BAC.∵AD平分∠FAC,∴∠DAC= ∠FAC.∴∠DAE= 又∵CD⊥AD,∴∠ADC=90°.∴四边形AECD是矩形.
6. C
7.证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC.∵BE=DF,∴AD-DF=BC-BE,即AF=EC.∴四边形AECF是平行四边形.又∵AC=EF,∴平行四边形 AECF 是矩形.
8. A 9. D 10.12 11.
12.解:(1)证明:∵AB=AC,D是BC 的中点,∴AD⊥BC,即∠ADC=∠ADB=90°.∵CE∥AD,∴∠ECD=∠ADB=90°.∵AE⊥AD,∴∠EAD=90°.∴∠ADC=∠ECD=∠EAD=90°.∴四边形ADCE是矩形.(2)∵D是BC 的中点, =2.由(1)可知,四边形ADCE是矩形,∴AE=CD=2,∠AEC=90°.在 Rt△AEC中,AE=2,CE=3,由勾股定理,得 AC=√AE +CE = .∵EF⊥AC,∴S△AEC= AC·EF= AE
13.解:(1)证明:由折叠的性质,得∠HEJ=∠AEH,∠BEF=∠FEJ,∴∠HEF=∠HEJ+∠FEJ= ×180°=90°.同理可得,∠EHG=∠HGF=∠EFG=90°,∴四边形 EFGH 是矩形. 5(cm).由折叠的性质,得 = CD,HD=HK,CF=KF,∴AE=CG.∵四边形EFGH是矩形,∴EH=GF.又∵∠A=∠C=90°,∴Rt△AEH≌Rt△CGF(HL).∴AH=CF.∴AH=KF.∴AD=AH+HD=FK+HK=HF=5cm.
