2024-2025学年人教版五年级数学下学期期末专题训练:图形计算题(含解析 )
文档属性
| 名称 | 2024-2025学年人教版五年级数学下学期期末专题训练:图形计算题(含解析 ) |  | |
| 格式 | docx | ||
| 文件大小 | 472.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 05:56:53 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
专题04 图形计算题(二)
1.计算下面长方体的体积。
2.求下面图形的表面积和体积。(单位:厘米)
3.求下面图形的表面积和体积。(单位:分米)
4.计算下面长方体和正方体的体积。(单位:厘米)
5.计算下面图形的体积。
6.仔细观察后计算出下面立体图形(小正方体的棱长是1厘米)的表面积和体积。
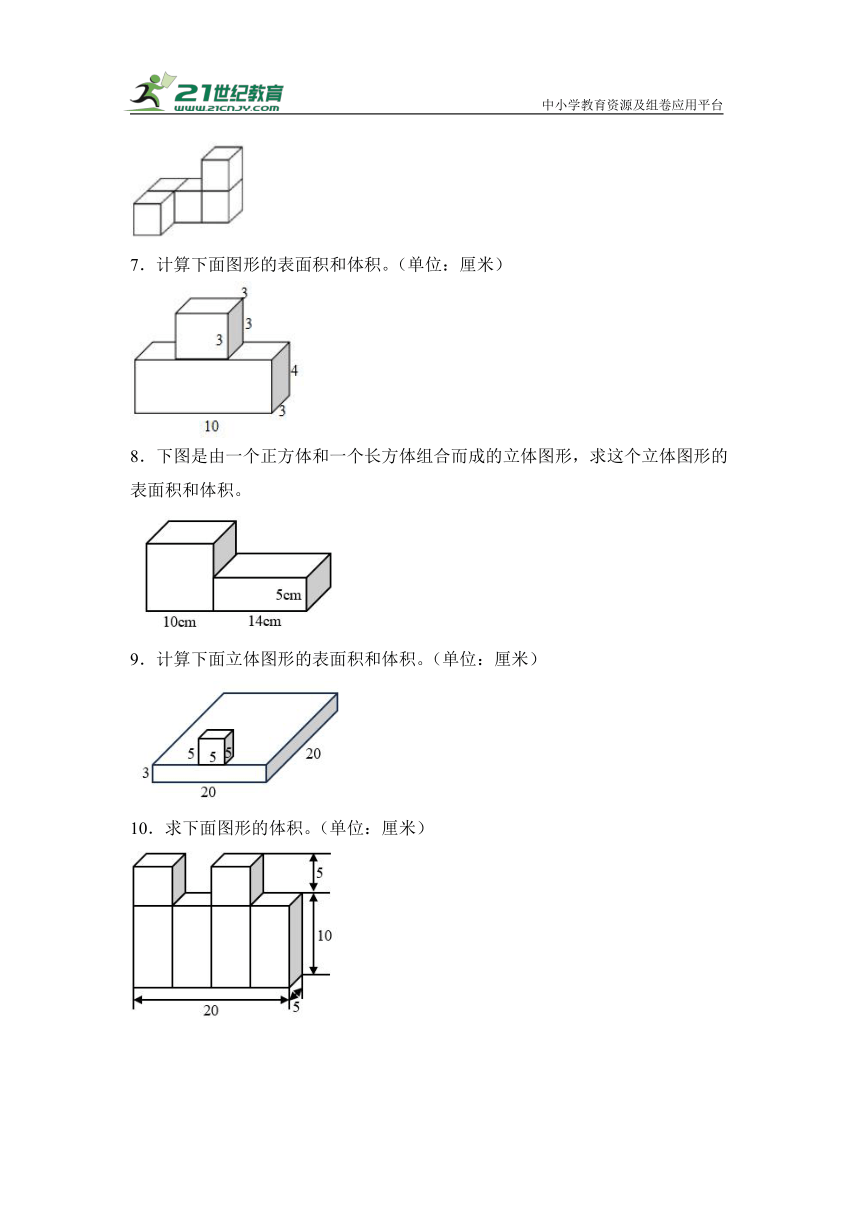
7.计算下面图形的表面积和体积。(单位:厘米)
8.下图是由一个正方体和一个长方体组合而成的立体图形,求这个立体图形的表面积和体积。
9.计算下面立体图形的表面积和体积。(单位:厘米)
10.求下面图形的体积。(单位:厘米)
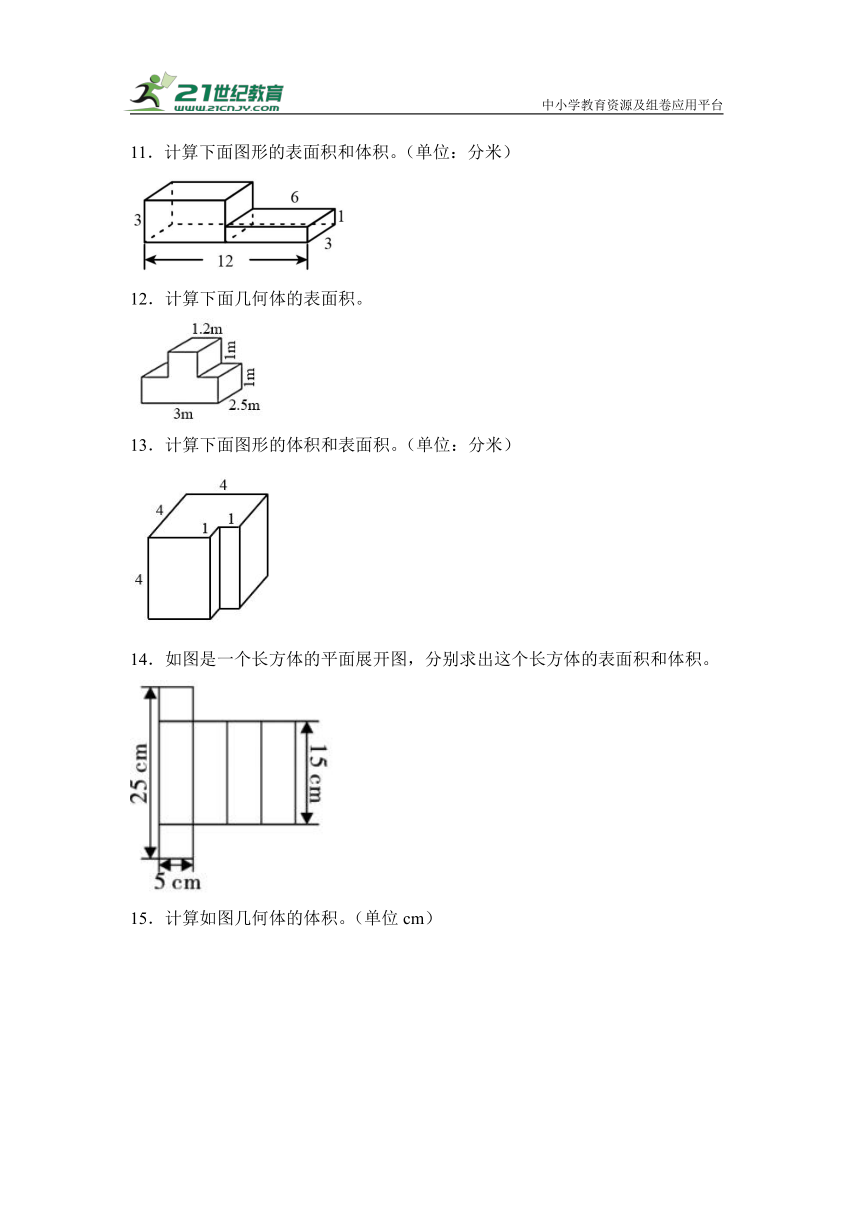
11.计算下面图形的表面积和体积。(单位:分米)
12.计算下面几何体的表面积。
13.计算下面图形的体积和表面积。(单位:分米)
14.如图是一个长方体的平面展开图,分别求出这个长方体的表面积和体积。
15.计算如图几何体的体积。(单位cm)
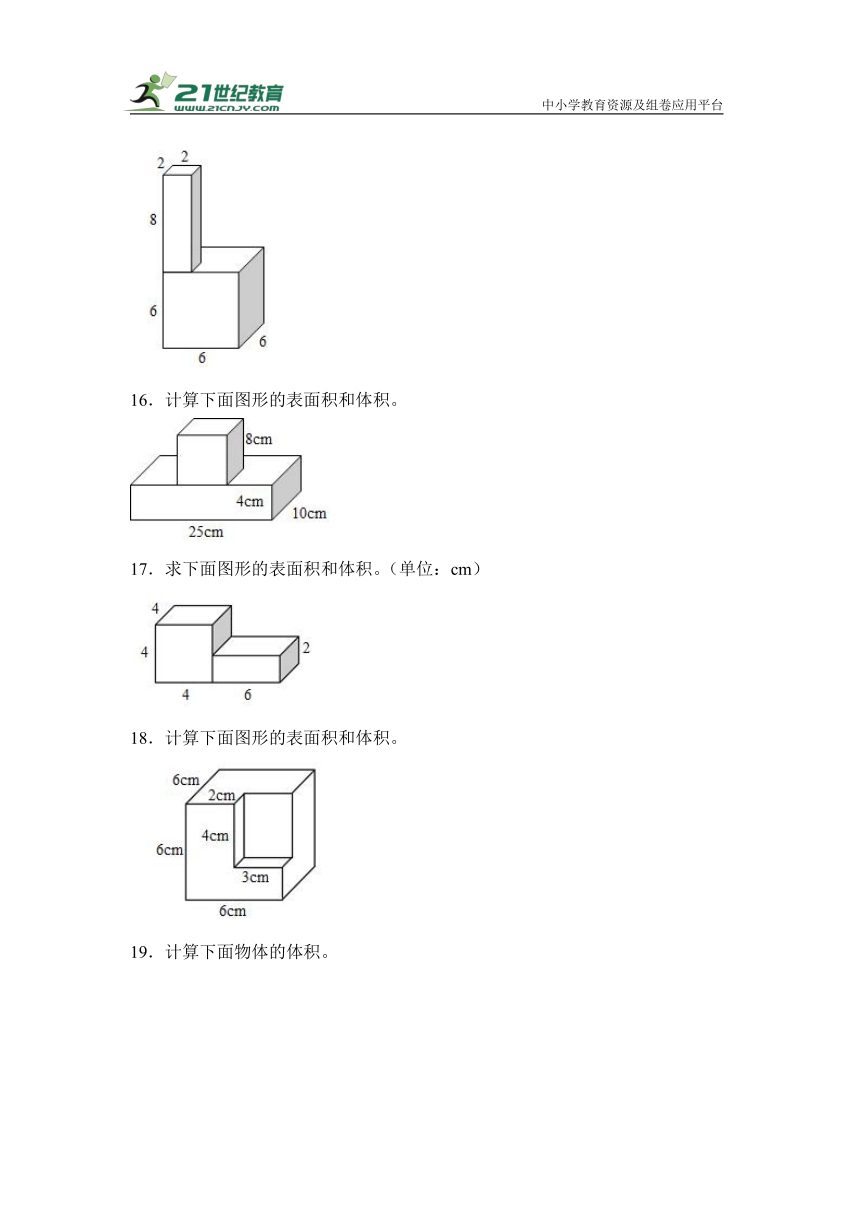
16.计算下面图形的表面积和体积。
17.求下面图形的表面积和体积。(单位:cm)
18.计算下面图形的表面积和体积。
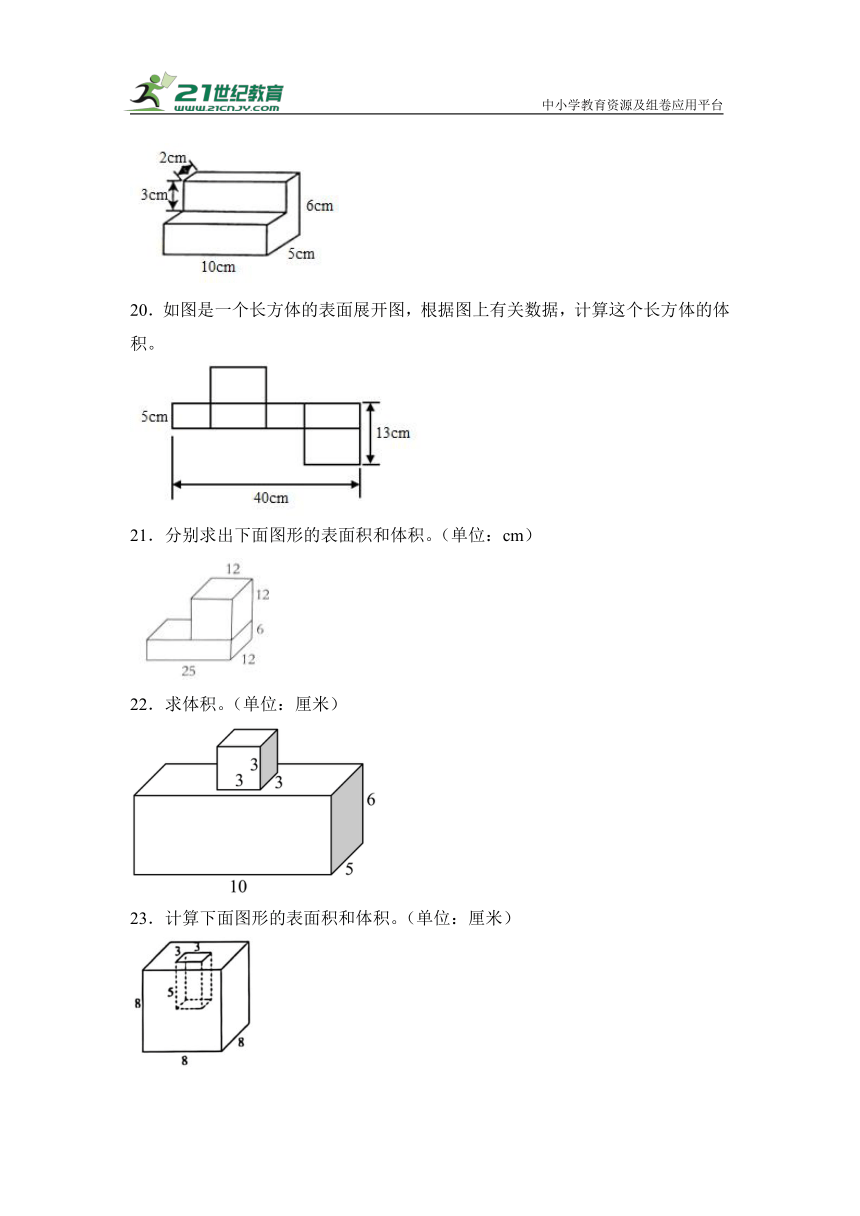
19.计算下面物体的体积。
20.如图是一个长方体的表面展开图,根据图上有关数据,计算这个长方体的体积。
21.分别求出下面图形的表面积和体积。(单位:cm)
22.求体积。(单位:厘米)
23.计算下面图形的表面积和体积。(单位:厘米)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《专题04 图形计算题(二)》参考答案
1.90cm3
【分析】根据长方体体积=长×宽×高,列式计算即可。
【详解】3×3×10=90(cm3)
长方体的体积是90cm3。
2.340平方厘米;392立方厘米
【分析】长方体的顶点处挖掉1个小正方体,看上去表面积减少了3个小正方形,又出现了同样的3个小正方形,因此这个图形的表面积=原来长方体的表面积,长方体的表面积=(长×宽+长×高+宽×高)×2;
这个图形的体积=长方体体积-正方体体积,长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,据此列式计算。
【详解】(10×5+10×8+5×8)×2
=(50+80+40)×2
=170×2
=340(平方厘米)
10×5×8-2×2×2
=400-8
=392(立方厘米)
这个图形的表面积是340平方厘米,体积是392立方厘米。
3.表面积124平方分米;体积75立方分米。
【分析】图形由一个棱长3分米的正方体和一个长6分米、宽4分米、高2分米的长方体叠加而成,图形的表面积是被遮挡了2个正方体的面,即长方体表面积+正方体的4个面面积,长方体表面积=(长×宽+长×高+宽×高)×2,据此计算出图形表面积;图形体积=长方体体积+正方体体积,长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,据此计算得出答案。
【详解】图形表面积为:
(平方分米)
体积为:
(立方分米)
4.4500立方厘米;64立方厘米
【分析】长方体体积=长×宽×高;正方体底面积=棱长×棱长,先确定正方体棱长,正方体体积=棱长×棱长×棱长,据此列式计算。
【详解】30×10×15=4500(立方厘米)
16=4×4
4×4×4=64(立方厘米)
长方体的体积是4500立方厘米,正方体的体积是64立方厘米。
5.475cm3
【分析】如下图,把图形的缺口补上,缺口处是一个棱长为5cm的正方体,则图形的体积=长方体的体积-正方体的体积;
根据长方体的体积公式V=abh,正方体的体积公式V=a3,代入数据计算求解。
【详解】12×10×5-5×5×5
=600-125
=475(cm3)
图形的体积是475cm3。
6.18平方厘米;5立方厘米
【分析】观察这个几何体,从前面、后面看,都能看到4个小正方形;从上面看,能看到4个小正方形;从左面、右面看,都能看到3个小正方形;所以露在外面的面共有(4+4+4+3+3)个面,一个面的面积是(1×1)平方厘米,再乘露在外面的面的个数即可求出这个图形的表面积;这个几何体是由5个小正方体组成,利用正方体的体积公式求出小正方体的体积,再乘5即可求出这个图形的体积。
【详解】1×1=1(平方厘米)
(4+4+4+3+3)×1
=18×1
=18(平方厘米)
1×1×1×5=5(立方厘米)
即立体图形的表面积是18平方厘米,体积是5立方厘米。
7.表面积是200平方厘米;体积是147立方厘米
【分析】看图可知,此图由一个长方体以及一个正方体组合而成,根据:长方体的表面积公式:2×,求出一个长方体的表面积以及一个正方体四个面的面积,即可算出整个图形的表面积;根据正方体的体积公式:,长方体的体积公式:,即可求出图形的体积。
【详解】长方体表面积:2×(10×3+10×4+3×4)
=2×(30+40+12)
=2×82
=164(平方厘米)
正方体四个面的面积:3×3×4
=9×4
=36(平方厘米)
图形表面积:164+36=200(平方厘米)
长方体体积:10×3×4
=30×4
=120(立方厘米)
正方体体积:3×3×3
=9×3
=27(立方厘米)
图形体积:120+27=147(立方厘米)
8.1020平方厘米;1700立方厘米
【分析】一个正方体和一个长方体叠加后,立体图形的表面积会在原来表面积的基础上,缺少两个(10×5)的面,用正方形的表面积加上长方体上下、前后4个面的面积之和,根据正方体的表面积和长方体的表面积公式即可得解。立体图形的体积等于正方体的体积加上长方体的体积,分别利用正方体的体积和长方体的体积的计算方法,即可得解。
【详解】表面积:10×10×6+(14×5+14×10)×2
=600+(70+140)×2
=600+210×2
=600+420
=1020(平方厘米)
体积:10×10×10+14×5×10
=1000+700
=1700(立方厘米)
即立体图形的表面积是1020平方厘米,体积是1700立方厘米。
9.表面积是1140平方厘米;体积是1325立方厘米
【分析】在长方体上面放一个小正方体,表面积比原来的长方体多了4个小正方形面的面积,每个正方形的边长是5厘米,根据长方体的表面积公式,用(20×20+20×3+20×3)×2即可求出原来长方体的表面积,再加上4个正方形面的面积,也就是5×5×4,即可求出这个立体图形的表面积;根据长方体的体积公式和正方体的体积公式,用20×20×3+5×5×5即可求出这个立体图形的体积。
【详解】(20×20+20×3+20×3)×2+5×5×4
=(400+60+60)×2+5×5×4
=520×2+5×5×4
=1040+100
=1140(平方厘米)
立体图形的表面积是1140平方厘米。
20×20×3+5×5×5
=1200+125
=1325(立方厘米)
立体图形的体积是1325立方厘米。
10.1250立方厘米
【分析】组合体的体积=大长方体的体积-2个棱长5厘米的正方体体积,长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,据此列式计算。
【详解】20×5×(10+5)-5×5×5×2
=100×15-250
=1500-250
=1250(立方厘米)
11.表面积是138平方分米,体积是72立方分米
【分析】两个长方体拼在一起,表面积比原来减少了2个长方形面,每个面长3厘米,宽1厘米;根据长方体的表面积=(长×宽+长×高+宽×高)×2,用[3×(12-6)+3×(12-6)+3×3]×2即可求出左边长方体原来的表面积,用[6×3+6×1+3×1]×2即可求出右边长方体原来的表面积,然后将两个长方体的表面积相加,再减去(3×1×2)平方厘米,即可求出立体图形的表面积;最后根据长方体的体积=长×宽×高,用(12-6)×3×3+6×3×1即可求出立体图形的体积。
【详解】[3×(12-6)+3×(12-6)+3×3]×2
=[3×6+3×6+3×3]×2
=[18+18+9]×2
=45×2
=90(平方分米)
[6×3+6×1+3×1]×2
=[18+6+3]×2
=27×2
=54(平方分米)
90+54-3×1×2
=90+54-6
=138(平方分米)
(12-6)×3×3+6×3×1
=6×3×3+6×3×1
=54+18
=72(立方分米)
立体图形的表面积是138平方分米,体积是72立方分米。
12.33.4m2
【分析】如图:
观察图形可知,两个长方体有重合的部分,把小长方体的上面向下平移,补给大长方体的上面;这样大长方体的表面积是6个面的面积之和,而小长方体只需计算4个面(前后面和左右面)的面积。
组合图形的表面积=小长方体4个面的面积+大长方体的表面积,小长方体4个面的面积=(长×高+宽×高)×2,大长方体的表面积=(长×宽+长×高+宽×高)×2,代入数据计算即可。
【详解】(1.2×1+2.5×1)×2+(3×2.5+3×1+2.5×1)×2
=(1.2+2.5)×2+(7.5+3+2.5)×2
=3.7×2+13×2
=7.4+26
=33.4(m2)
几何体的表面积是33.4m2。
13.60立方分米;94平方分米
【分析】通过观察可知,该图形可以看作一个棱长为4分米的正方体切去了一个底面边长为1分米,高为4分米的长方体,计算它的体积时直接用正方体体积减去长方体体积即可;从上下前后左右六个方向整体观察可知,它的表面积相当于正方体的表面积减去两个边长为1分米的正方形的面积(上下两个面各缺少一个)。
【详解】体积:
4×4×4-1×1×4
=64-4
=60(立方分米)
表面积:
4×4×6-1×1×2
=96-2
=94(平方分米)
14.350cm2;375cm3
【分析】根据长方体的展开图可知,这个长方体的长是15cm,宽是5cm,高是:(25-15)÷2=5cm;再根据长方体的表面积和体积公式计算即可。
【详解】(25-15)÷2
=10÷2
=5(cm)
(15×5+15×5+5×5)×2
=(75+75+25)×2
=175×2
=350(cm2)
15×5×5
=75×5
=375(cm3)
15.248cm3
【分析】观察图形可知,该图形的体积=长方体的体积+正方体的体积,根据正方体的体积公式:V=a3,长方体的体积公式:V=abh,据此代入数值进行计算即可。
【详解】6×6×6+2×2×8
=36×6+4×8
=216+32
=248(cm3)
16.1036平方厘米;1512立方厘米
【分析】通过对立体图形的分析,正方体和长方体拼起来后比单独放时表面积减少了2个正方形面,根据长方体和正方体的表面积公式,分别计算出长方体和正方体的表面积,再减去2个正方形的面积即可,即(25×10+25×4+10×4)×2+8×8×6-8×8×2=1036(平方厘米);正方体和长方体拼起来后体积不变,所以根据长方体和正方体的体积公式,分别求出长方体的体积和正方体的体积,再相加即可,即25×10×4+8×8×8=1512(立方厘米)。
【详解】(25×10+25×4+10×4)×2+8×8×6-8×8×2
=(250+100+40)×2+384-128
=780+384-128
=1036(平方厘米)
25×10×4+8×8×8
=1000+512
=1512(立方厘米)
所以立体图形的表面积是1036平方厘米;体积是512立方厘米。
17.表面积168cm2;体积112cm3
【分析】从图中可知,左边是正方体,右边是长方体,正方体和长方体有重合部分;把长方体的右面平移到重合处,补给正方体的右面,这样正方体的表面积是6个面的面积之和,长方体的表面积只有上下面、前后面共4个面的面积之和;
图形的表面积=正方体的表面积+长方体4个面的面积;根据正方体的表面积=棱长×棱长×6,长方体的4个面的面积=长×宽×2+长×高×2,代入数据计算即可。
图形的体积=正方体的体积+长方体的体积,根据正方体的体积=棱长×棱长×棱长,长方体的体积=长×宽×高,代入数据计算即可。
【详解】图形的表面积:
4×4×6
=16×6
=96(cm2)
6×4×2+6×2×2
=24×2+12×2
=48+24
=72(cm2)
96+72=168(cm2)
图形的体积:
4×4×4
=16×4
=64(cm3)
6×4×2
=24×2
=48(cm3)
64+48=112(cm3)
18.216cm2;192cm3
【分析】由图可知,用棱长为6cm的正方体减去长3cm、宽2cm、高4cm的长方体就是这个几何体的体积;又知这个几何体的表面积就是棱长为6cm的正方体的表面积,根据长方体的体积、和正方体表面积、体积公式,代入数据进行解答即可。
【详解】6×6×6-2×4×3
=36×6-8×3
=216-24
=192(cm3)
6×6×6
=36×6
=216(cm2)
19.210cm3
【分析】把组合图形拆解成两个长方体,其中一个长方体的长为10cm,宽为5cm,高为(6-3)cm,另一个长方体的长为10cm,宽为2cm,高为3cm,利用长方体的体积=长×宽×高,分别把这些数据代入到公式中,求出两个长方体的体积,再相加即可得解。
【详解】10×5×(6-3)+10×2×3
=50×3+20×3
=150+60
=210(cm3)
20.
【分析】由展开图分析出长方体的长、宽、高,再根据长方体体积长宽高,计算即可。
【详解】宽:
高为。
长:
体积:
21.表面积:1620cm2;
体积:3528cm3
【分析】(1)立体图形的表面积为长方体的表面积加上正方体的四个面的面积和;
(2)立体图形的体积为长方体的体积与正方体的体积之和。
【详解】表面积:
12×12×4+(25×12+25×6+12×6)×2
=576+1044
=1620(cm )
体积:12×12×12+25×12×6
=1728+1800
=3528(cm )
22.327立方厘米
【分析】组合体的体积=长方体体积+正方体体积,长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长。
【详解】10×5×6+3×3×3
=300+27
=327(立方厘米)
23.444平方厘米;467立方厘米
【分析】组合体的表面积=完整的大正方体表面积+长方体前后左右4个面的面积,正方体表面积=棱长×棱长×6,长方体前后左右4个面的面积=长×高×4;组合体的体积=大正方体体积-长方体体积,正方体体积=棱长×棱长×棱长,长方体体积=长×宽×高,据此列式计算。
【详解】8×8×6+3×5×4
=384+60
=444(平方厘米)
8×8×8-3×3×5
=512-45
=467(立方厘米)
组合体的表面积是444平方厘米,组合体的体积是467立方厘米。
答案第2页,共11页
答案第11页,共11页
中小学教育资源及组卷应用平台
专题04 图形计算题(二)
1.计算下面长方体的体积。
2.求下面图形的表面积和体积。(单位:厘米)
3.求下面图形的表面积和体积。(单位:分米)
4.计算下面长方体和正方体的体积。(单位:厘米)
5.计算下面图形的体积。
6.仔细观察后计算出下面立体图形(小正方体的棱长是1厘米)的表面积和体积。
7.计算下面图形的表面积和体积。(单位:厘米)
8.下图是由一个正方体和一个长方体组合而成的立体图形,求这个立体图形的表面积和体积。
9.计算下面立体图形的表面积和体积。(单位:厘米)
10.求下面图形的体积。(单位:厘米)
11.计算下面图形的表面积和体积。(单位:分米)
12.计算下面几何体的表面积。
13.计算下面图形的体积和表面积。(单位:分米)
14.如图是一个长方体的平面展开图,分别求出这个长方体的表面积和体积。
15.计算如图几何体的体积。(单位cm)
16.计算下面图形的表面积和体积。
17.求下面图形的表面积和体积。(单位:cm)
18.计算下面图形的表面积和体积。
19.计算下面物体的体积。
20.如图是一个长方体的表面展开图,根据图上有关数据,计算这个长方体的体积。
21.分别求出下面图形的表面积和体积。(单位:cm)
22.求体积。(单位:厘米)
23.计算下面图形的表面积和体积。(单位:厘米)
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
《专题04 图形计算题(二)》参考答案
1.90cm3
【分析】根据长方体体积=长×宽×高,列式计算即可。
【详解】3×3×10=90(cm3)
长方体的体积是90cm3。
2.340平方厘米;392立方厘米
【分析】长方体的顶点处挖掉1个小正方体,看上去表面积减少了3个小正方形,又出现了同样的3个小正方形,因此这个图形的表面积=原来长方体的表面积,长方体的表面积=(长×宽+长×高+宽×高)×2;
这个图形的体积=长方体体积-正方体体积,长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,据此列式计算。
【详解】(10×5+10×8+5×8)×2
=(50+80+40)×2
=170×2
=340(平方厘米)
10×5×8-2×2×2
=400-8
=392(立方厘米)
这个图形的表面积是340平方厘米,体积是392立方厘米。
3.表面积124平方分米;体积75立方分米。
【分析】图形由一个棱长3分米的正方体和一个长6分米、宽4分米、高2分米的长方体叠加而成,图形的表面积是被遮挡了2个正方体的面,即长方体表面积+正方体的4个面面积,长方体表面积=(长×宽+长×高+宽×高)×2,据此计算出图形表面积;图形体积=长方体体积+正方体体积,长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,据此计算得出答案。
【详解】图形表面积为:
(平方分米)
体积为:
(立方分米)
4.4500立方厘米;64立方厘米
【分析】长方体体积=长×宽×高;正方体底面积=棱长×棱长,先确定正方体棱长,正方体体积=棱长×棱长×棱长,据此列式计算。
【详解】30×10×15=4500(立方厘米)
16=4×4
4×4×4=64(立方厘米)
长方体的体积是4500立方厘米,正方体的体积是64立方厘米。
5.475cm3
【分析】如下图,把图形的缺口补上,缺口处是一个棱长为5cm的正方体,则图形的体积=长方体的体积-正方体的体积;
根据长方体的体积公式V=abh,正方体的体积公式V=a3,代入数据计算求解。
【详解】12×10×5-5×5×5
=600-125
=475(cm3)
图形的体积是475cm3。
6.18平方厘米;5立方厘米
【分析】观察这个几何体,从前面、后面看,都能看到4个小正方形;从上面看,能看到4个小正方形;从左面、右面看,都能看到3个小正方形;所以露在外面的面共有(4+4+4+3+3)个面,一个面的面积是(1×1)平方厘米,再乘露在外面的面的个数即可求出这个图形的表面积;这个几何体是由5个小正方体组成,利用正方体的体积公式求出小正方体的体积,再乘5即可求出这个图形的体积。
【详解】1×1=1(平方厘米)
(4+4+4+3+3)×1
=18×1
=18(平方厘米)
1×1×1×5=5(立方厘米)
即立体图形的表面积是18平方厘米,体积是5立方厘米。
7.表面积是200平方厘米;体积是147立方厘米
【分析】看图可知,此图由一个长方体以及一个正方体组合而成,根据:长方体的表面积公式:2×,求出一个长方体的表面积以及一个正方体四个面的面积,即可算出整个图形的表面积;根据正方体的体积公式:,长方体的体积公式:,即可求出图形的体积。
【详解】长方体表面积:2×(10×3+10×4+3×4)
=2×(30+40+12)
=2×82
=164(平方厘米)
正方体四个面的面积:3×3×4
=9×4
=36(平方厘米)
图形表面积:164+36=200(平方厘米)
长方体体积:10×3×4
=30×4
=120(立方厘米)
正方体体积:3×3×3
=9×3
=27(立方厘米)
图形体积:120+27=147(立方厘米)
8.1020平方厘米;1700立方厘米
【分析】一个正方体和一个长方体叠加后,立体图形的表面积会在原来表面积的基础上,缺少两个(10×5)的面,用正方形的表面积加上长方体上下、前后4个面的面积之和,根据正方体的表面积和长方体的表面积公式即可得解。立体图形的体积等于正方体的体积加上长方体的体积,分别利用正方体的体积和长方体的体积的计算方法,即可得解。
【详解】表面积:10×10×6+(14×5+14×10)×2
=600+(70+140)×2
=600+210×2
=600+420
=1020(平方厘米)
体积:10×10×10+14×5×10
=1000+700
=1700(立方厘米)
即立体图形的表面积是1020平方厘米,体积是1700立方厘米。
9.表面积是1140平方厘米;体积是1325立方厘米
【分析】在长方体上面放一个小正方体,表面积比原来的长方体多了4个小正方形面的面积,每个正方形的边长是5厘米,根据长方体的表面积公式,用(20×20+20×3+20×3)×2即可求出原来长方体的表面积,再加上4个正方形面的面积,也就是5×5×4,即可求出这个立体图形的表面积;根据长方体的体积公式和正方体的体积公式,用20×20×3+5×5×5即可求出这个立体图形的体积。
【详解】(20×20+20×3+20×3)×2+5×5×4
=(400+60+60)×2+5×5×4
=520×2+5×5×4
=1040+100
=1140(平方厘米)
立体图形的表面积是1140平方厘米。
20×20×3+5×5×5
=1200+125
=1325(立方厘米)
立体图形的体积是1325立方厘米。
10.1250立方厘米
【分析】组合体的体积=大长方体的体积-2个棱长5厘米的正方体体积,长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,据此列式计算。
【详解】20×5×(10+5)-5×5×5×2
=100×15-250
=1500-250
=1250(立方厘米)
11.表面积是138平方分米,体积是72立方分米
【分析】两个长方体拼在一起,表面积比原来减少了2个长方形面,每个面长3厘米,宽1厘米;根据长方体的表面积=(长×宽+长×高+宽×高)×2,用[3×(12-6)+3×(12-6)+3×3]×2即可求出左边长方体原来的表面积,用[6×3+6×1+3×1]×2即可求出右边长方体原来的表面积,然后将两个长方体的表面积相加,再减去(3×1×2)平方厘米,即可求出立体图形的表面积;最后根据长方体的体积=长×宽×高,用(12-6)×3×3+6×3×1即可求出立体图形的体积。
【详解】[3×(12-6)+3×(12-6)+3×3]×2
=[3×6+3×6+3×3]×2
=[18+18+9]×2
=45×2
=90(平方分米)
[6×3+6×1+3×1]×2
=[18+6+3]×2
=27×2
=54(平方分米)
90+54-3×1×2
=90+54-6
=138(平方分米)
(12-6)×3×3+6×3×1
=6×3×3+6×3×1
=54+18
=72(立方分米)
立体图形的表面积是138平方分米,体积是72立方分米。
12.33.4m2
【分析】如图:
观察图形可知,两个长方体有重合的部分,把小长方体的上面向下平移,补给大长方体的上面;这样大长方体的表面积是6个面的面积之和,而小长方体只需计算4个面(前后面和左右面)的面积。
组合图形的表面积=小长方体4个面的面积+大长方体的表面积,小长方体4个面的面积=(长×高+宽×高)×2,大长方体的表面积=(长×宽+长×高+宽×高)×2,代入数据计算即可。
【详解】(1.2×1+2.5×1)×2+(3×2.5+3×1+2.5×1)×2
=(1.2+2.5)×2+(7.5+3+2.5)×2
=3.7×2+13×2
=7.4+26
=33.4(m2)
几何体的表面积是33.4m2。
13.60立方分米;94平方分米
【分析】通过观察可知,该图形可以看作一个棱长为4分米的正方体切去了一个底面边长为1分米,高为4分米的长方体,计算它的体积时直接用正方体体积减去长方体体积即可;从上下前后左右六个方向整体观察可知,它的表面积相当于正方体的表面积减去两个边长为1分米的正方形的面积(上下两个面各缺少一个)。
【详解】体积:
4×4×4-1×1×4
=64-4
=60(立方分米)
表面积:
4×4×6-1×1×2
=96-2
=94(平方分米)
14.350cm2;375cm3
【分析】根据长方体的展开图可知,这个长方体的长是15cm,宽是5cm,高是:(25-15)÷2=5cm;再根据长方体的表面积和体积公式计算即可。
【详解】(25-15)÷2
=10÷2
=5(cm)
(15×5+15×5+5×5)×2
=(75+75+25)×2
=175×2
=350(cm2)
15×5×5
=75×5
=375(cm3)
15.248cm3
【分析】观察图形可知,该图形的体积=长方体的体积+正方体的体积,根据正方体的体积公式:V=a3,长方体的体积公式:V=abh,据此代入数值进行计算即可。
【详解】6×6×6+2×2×8
=36×6+4×8
=216+32
=248(cm3)
16.1036平方厘米;1512立方厘米
【分析】通过对立体图形的分析,正方体和长方体拼起来后比单独放时表面积减少了2个正方形面,根据长方体和正方体的表面积公式,分别计算出长方体和正方体的表面积,再减去2个正方形的面积即可,即(25×10+25×4+10×4)×2+8×8×6-8×8×2=1036(平方厘米);正方体和长方体拼起来后体积不变,所以根据长方体和正方体的体积公式,分别求出长方体的体积和正方体的体积,再相加即可,即25×10×4+8×8×8=1512(立方厘米)。
【详解】(25×10+25×4+10×4)×2+8×8×6-8×8×2
=(250+100+40)×2+384-128
=780+384-128
=1036(平方厘米)
25×10×4+8×8×8
=1000+512
=1512(立方厘米)
所以立体图形的表面积是1036平方厘米;体积是512立方厘米。
17.表面积168cm2;体积112cm3
【分析】从图中可知,左边是正方体,右边是长方体,正方体和长方体有重合部分;把长方体的右面平移到重合处,补给正方体的右面,这样正方体的表面积是6个面的面积之和,长方体的表面积只有上下面、前后面共4个面的面积之和;
图形的表面积=正方体的表面积+长方体4个面的面积;根据正方体的表面积=棱长×棱长×6,长方体的4个面的面积=长×宽×2+长×高×2,代入数据计算即可。
图形的体积=正方体的体积+长方体的体积,根据正方体的体积=棱长×棱长×棱长,长方体的体积=长×宽×高,代入数据计算即可。
【详解】图形的表面积:
4×4×6
=16×6
=96(cm2)
6×4×2+6×2×2
=24×2+12×2
=48+24
=72(cm2)
96+72=168(cm2)
图形的体积:
4×4×4
=16×4
=64(cm3)
6×4×2
=24×2
=48(cm3)
64+48=112(cm3)
18.216cm2;192cm3
【分析】由图可知,用棱长为6cm的正方体减去长3cm、宽2cm、高4cm的长方体就是这个几何体的体积;又知这个几何体的表面积就是棱长为6cm的正方体的表面积,根据长方体的体积、和正方体表面积、体积公式,代入数据进行解答即可。
【详解】6×6×6-2×4×3
=36×6-8×3
=216-24
=192(cm3)
6×6×6
=36×6
=216(cm2)
19.210cm3
【分析】把组合图形拆解成两个长方体,其中一个长方体的长为10cm,宽为5cm,高为(6-3)cm,另一个长方体的长为10cm,宽为2cm,高为3cm,利用长方体的体积=长×宽×高,分别把这些数据代入到公式中,求出两个长方体的体积,再相加即可得解。
【详解】10×5×(6-3)+10×2×3
=50×3+20×3
=150+60
=210(cm3)
20.
【分析】由展开图分析出长方体的长、宽、高,再根据长方体体积长宽高,计算即可。
【详解】宽:
高为。
长:
体积:
21.表面积:1620cm2;
体积:3528cm3
【分析】(1)立体图形的表面积为长方体的表面积加上正方体的四个面的面积和;
(2)立体图形的体积为长方体的体积与正方体的体积之和。
【详解】表面积:
12×12×4+(25×12+25×6+12×6)×2
=576+1044
=1620(cm )
体积:12×12×12+25×12×6
=1728+1800
=3528(cm )
22.327立方厘米
【分析】组合体的体积=长方体体积+正方体体积,长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长。
【详解】10×5×6+3×3×3
=300+27
=327(立方厘米)
23.444平方厘米;467立方厘米
【分析】组合体的表面积=完整的大正方体表面积+长方体前后左右4个面的面积,正方体表面积=棱长×棱长×6,长方体前后左右4个面的面积=长×高×4;组合体的体积=大正方体体积-长方体体积,正方体体积=棱长×棱长×棱长,长方体体积=长×宽×高,据此列式计算。
【详解】8×8×6+3×5×4
=384+60
=444(平方厘米)
8×8×8-3×3×5
=512-45
=467(立方厘米)
组合体的表面积是444平方厘米,组合体的体积是467立方厘米。
答案第2页,共11页
答案第11页,共11页
同课章节目录
