2024-2025学年苏科版八年级数学下册期末真题专项练习 05 解答题(含解析)
文档属性
| 名称 | 2024-2025学年苏科版八年级数学下册期末真题专项练习 05 解答题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 816.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 08:55:17 | ||
图片预览



文档简介
2024-2025学年苏科版八年级数学下册期末真题
专项练习 05 解答题
一、解答题
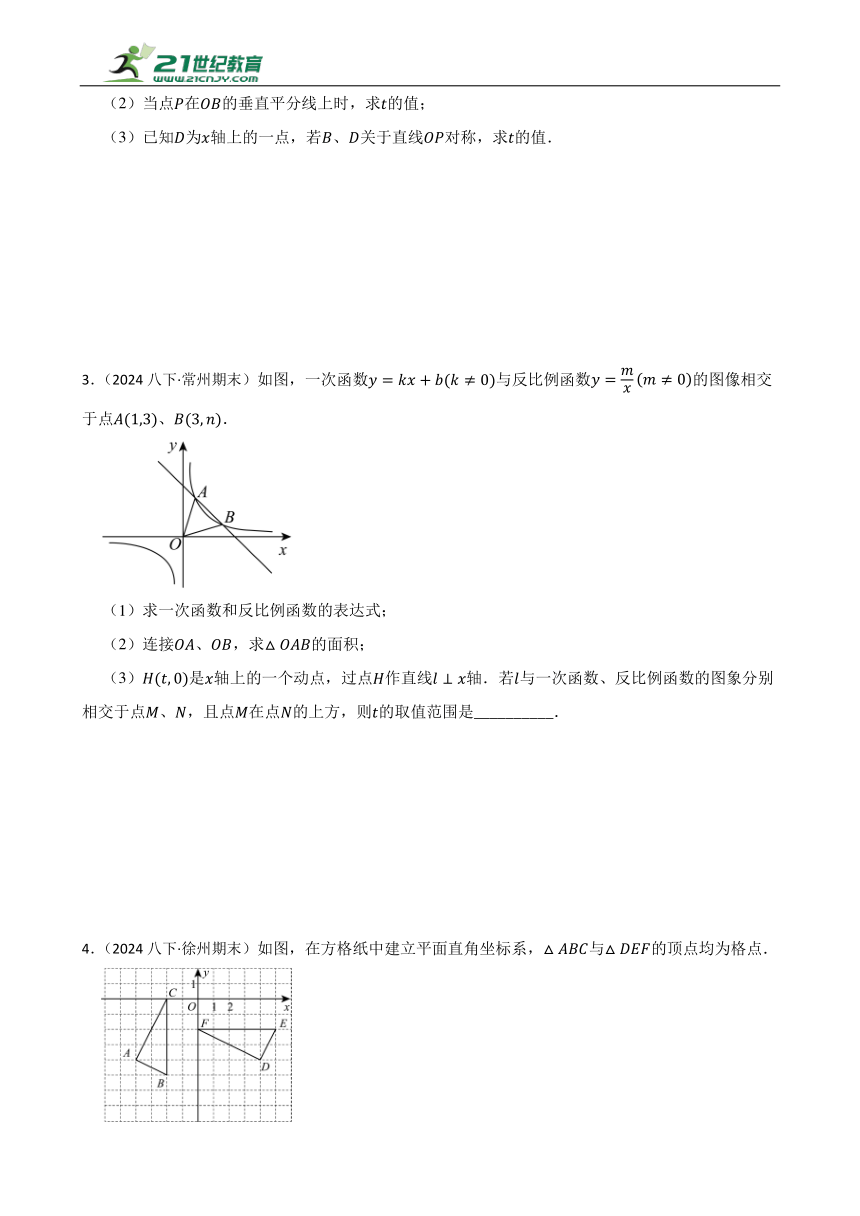
1.(2024八下·南京期末)如图,反比例函数与一次函数的图象交于点、点.
(1)反比例函数为 ,一次函数为 ,不等式的解集为 ;
(2)点E为y轴上一个动点,若,求点E的坐标.
(3)若将一次函数的图像沿y轴向下平移n个单位,使平移后的图像与反比例函数的图像有且只有一个交点,则n的值是 .
2.(2024八下·扬州期末)如图,在平面直角坐标系中,四边形为矩形,点,.动点从点出发,以每秒1个单位长的速度沿射线方向匀速运动,设运动时间为秒.
(1)当______秒时,以、为邻边的平行四边形是菱形;
(2)当点在的垂直平分线上时,求的值;
(3)已知为轴上的一点,若、关于直线对称,求的值.
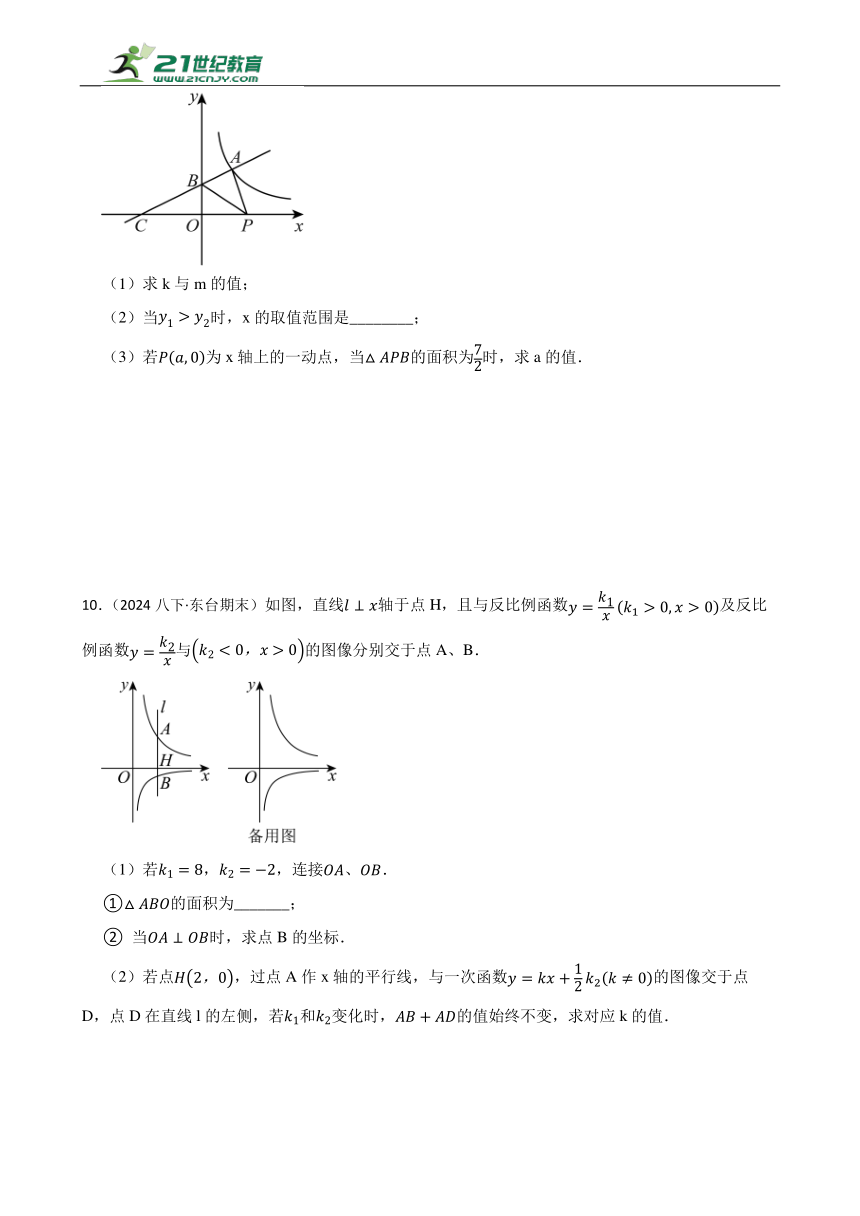
3.(2024八下·常州期末)如图,一次函数与反比例函数的图像相交于点、.
(1)求一次函数和反比例函数的表达式;
(2)连接、,求的面积;
(3)是轴上的一个动点,过点作直线轴.若与一次函数、反比例函数的图象分别相交于点、,且点在点的上方,则的取值范围是__________.
4.(2024八下·徐州期末)如图,在方格纸中建立平面直角坐标系,与的顶点均为格点.
(1)若绕点逆时针旋转可得到,则旋转角至少为______;
(2)将绕点顺时针旋转得到,画出;
(3)若(2)中的与成中心对称,则对称中心的坐标为______.
5.(2024八下·姑苏期末)如图,一次函数的图象与反比例函数的图象交于,两点,与x轴交于点C.
(1)求一次函数与反比例函数的解析式;
(2)连接,求的面积.
6.(2024八下·海安期末)在平面直角坐标系中,点在直线上.
(1)直线与轴的交点坐标为________;
(2)矩形的顶点分别轴,轴上.
①当,时,求矩形的面积;
②若使矩形的面积为4的点恰好有4个,试求的取值范围.
7.(2024八下·海安期末)为保障旅客快捷、安全的出入车站,海安火车站修建了四个自动检票口,分别记为A、B、C、D.当甲、乙两名乘客通过该站检票口时,请回答下列问题:
(1)甲通过A检票口的概率是________;
(2)用树状图或列表法求甲、乙两名乘客选择不同检票口通过的概率.
8.(2024八下·广陵期末)某中学为配合开展“垃圾分类进校园”活动,新购买了一批不同型号的垃圾分类桶,学校先用4050元购买了一批给班级使用的小号垃圾桶,再用5400元购买了一批放在户外永久使用的大号垃圾桶,已知每个大号垃圾桶的价格是小号垃圾桶的4倍,且购买的数量比小号垃圾桶少60个,求每个小号垃圾桶的价格是多少元?
9.(2024八下·扬州期末)如图,一次函数的图像与反比例函数(,)的图像交于点,与y轴交于点B,与x轴交于点.
(1)求k与m的值;
(2)当时,x的取值范围是________;
(3)若为x轴上的一动点,当的面积为时,求a的值.
10.(2024八下·东台期末)如图,直线轴于点H,且与反比例函数及反比例函数与的图像分别交于点A、B.
(1)若,,连接、.
①的面积为_______;
② 当时,求点B的坐标.
(2)若点,过点A作x轴的平行线,与一次函数的图像交于点D,点D在直线l的左侧,若和变化时,的值始终不变,求对应k的值.
11.(2024八下·惠山期末)如图,平行四边形中,,,点以的速度从点出发沿向点运动,同时点以的速度从点出发沿向点运动,当一个点到达终点时,另一个点也停止运动,设运动的时间为.
(1)求平行四边形的面积;
(2)当的面积为平行四边形的面积的时,求的值;
(3)当时,连接,取线段的中点,请直接写出的长度.
12.(2024八下·惠山期末)如图,在平面直角坐标系中,直线与轴正半轴与轴正半轴分别交于点、,设,(,).将绕点顺时针方向旋转得到,点的对应点为点;再将沿射线方向平移,使点与点重合得到,点的对应点为点,点在轴上,点为线段的中点,点与点恰好落在同一个反比例函数的图象上.
(1)当时,求反比例函数的解析式.
(2)求的值.
(3)若线段、交于点,且的面积为,求的值.
13.(2024八下·姑苏期末)如图,在中,,点A的坐标为,点在反比例函数的图象上.若将线段AB绕点A按顺时针方向旋转90°,得到线段AC,点C恰好在反比例函数的图象上.
(1)求,的值;
(2)若P,Q分别为反比例函数,图象上一点,且以点O,P,Q,A为顶点的四边形为平行四边形,求点P的坐标.
14.(2024八下·苏州工业园期末)如图1,四边形ABCD为正方形,点A在y轴上,点B在x轴上,且OA=6,OB=3,反比例函数在第一象限的图象经过正方形的顶点C.
(1)求点C的坐标和反比例函数的表达式;
(2)如图2,将正方形ABCD沿x轴向右平移m个单位长度得到正方形,点恰好落在反比例函数的图象上,求此时点的坐标;
(3)在(2)的条件下,点P为x轴上一动点,平面内是否存在点Q,使以点O、、P、Q为顶点的四边形为菱形,若存在,请直接写出点Q的坐标,若不存在,请说明理由.
15.(2024八下·吴江期末)在矩形中,,,点是边上的一个动点,,垂足为的延长线交于点.
(1)如图1,延长,若三点在一直线上,,求的长;
(2)过点作,垂足为:
①如图2,若,,求的面积;
②如图3,若,连接,则的值为______.
16.(2024八下·吴江期末)如图,在平面直角坐标系中,已知点,点是线段上的一个动点,过点作轴,交反比例函数的图象于点,过点作的垂线交轴于点,是线段上一点,且,连接,设点的横坐标为.
(1)点的坐标为______;(用含的代数式表示)
(2)若,求点的坐标;
(3)若的面积为3时,点也在反比例函数的图象上,求的值.
17.(2024八下·吴江期末)公元前3世纪,古希腊学者阿基米德发现了著名的“杠杆原理”.杠杆平衡时,阻力阻力臂动力动力臂.几位同学玩撬石头的游戏,已知阻力(石头重量)和阻力臂分别为和.
(1)设动力臂为,动力为,求出与的函数表达式;
(2)若小明使用的力量,他该选择动力臂为多少米的撬棍正好能撬动这块大石头?
18.(2024八下·海门期末)如图,在平面直角坐标系中,直线与x轴,y轴分别交于点A,B,以为边作正方形.
(1)当时,求点C,D的坐标;
(2)当点C的纵坐标为7时,求m的值:
(3)当点C一定不落在第二象限时,直接写出m的取值范围.
19.(2024八下·泰州医药高新技术产业开发期末)如图,在矩形纸片中,E为边上的动点,F为边上的动点,连接.
(1)若.
①如图①,点E与点D重合,点F与点B重合,将矩形纸片沿折叠,点A落在点G处,设与相交于H,求的长;
②如图②,将矩形纸片沿折叠,使点B与点D重合,求折痕的长;
(2)如图③,点E为的中点,点F与点B重合,将矩形纸片沿折叠,点A落在点G处,且点G在矩形内部,延长交于点H,若,求的值.
20.(2024八下·徐州期末)如图,已知一次函数与反比例函数的图象交于点.
(1)求一次函数和反比例函数的表达式;
(2)根据图象,直接写出使成立的自变量的取值范围______.
21.(2024八下·连云港期末)某校学生健康活动中心通过调查,形成了如下调查报告(不完整).
调查目的 1. 为配合卫生部门的“正脊行动”,提前了解全校学生脊柱健康状况 2. 为全校学生保护脊柱健康提出合理建议
调查方式 随机抽样调查 调查对象 本校部分学生
调查内容 该生的脊柱健康状况的检查结果是: A. 正常 B. 轻度侧弯 C. 中度侧弯 D. 重度侧弯
调查结果 学生脊柱健康状况统计表
类型 A B C D 频数(人数) 频率
85 0.85
11 0.11
3 0.03
1 0.01
建议 ……
结合调查信息,回答下列问题:
(1)本次调查共抽查 名学生;
(2)小明用扇形统计图对统计数据进行重新整理,则在小明要画的扇形统计图中,脊柱健康结果为C所对应的扇形圆心角的度数是 °;
(3)若该校共有1800名学生,请估计该校脊柱侧弯程度为中度和重度的总人数是多少?
(4)假如你是学生健康中心成员,请你向该校提一条合理建议.
22.(2024八下·新吴期末)劳动教育是新时代党对教育的新要求,某校为了解学生参加家务劳动的情况,随机抽取了部分学生在某个星期日做家务的时间(单位:)作为样本,将收集的数据整理后分为、、、、五个组别,其中组的数据分别为:0.5,0.4,0.4,0.4,0.3,绘制成如下不完整的统计图表.
各组劳动时间的频数分布表
组别 时间 频数
5
20
15
8
各组劳动时间的扇形统计图
请根据以上信息解答下列问题.
(1)本次调查的样本容量为________,频数分布表中的的值为________;
(2)组所在扇形的圆心角的大小为________;
(3)若该校有1200名学生,估计该校学生劳动时间超过的人数.
23.(2024八下·海陵期末)如图,菱形的顶点A的坐标为,顶点O与坐标原点重合,顶点B在x轴正半轴上,点D是的中点,反比例函数的图像经过点D.
(1)求的长及k的值;
(2)反比例的图像上存在点E,使得的面积为,求点E的坐标.
24.(2024八下·沛县期末)如图,在平面直角坐标系中,正比例函数的图像与反比例函数的图像交于、两点.
(1)求的值;
(2)当时,的取值范围是__________;
(3)当时,的取值范围是__________;
(4)若轴上存在点,使得的面积为,求点的坐标.
25.(2024八下·太仓期末)如图,一次函数的图像与x轴交于点A,与反比例函数的图像交于点,过点B作轴,垂足为点C,点P是反比例函数的图像上的一点,且.
(1)求反比例函数的表达式;
(2)求点P的坐标.
26.(2024八下·太仓期末)如图,四边形是矩形,点P为边上一动点(与点C,D不重合),连接,过点A作交的延长线于点Q,连接,交于点E.设,.
(1)当,时.
①若点P是中点时,求的长;
②若是等腰三角形,求的长;
(2)取的中点M,连接,若在点P运动过程中存在某一位置,使得四边形是平行四边形,则m,n之间的数量关系为______.
27.(2024八下·秦淮期末)对于两个不同的函数,通过减法运算可以得到一个新函数,我们把这个新函数称为两个函数的“差函数”.例如:对于函数和,则函数,的“差函数”记为.
(1)已知函数和,若将这两个函数的“差函数”记为;
①写出的表达式, ;
②函数,的图象如图①所示,则的大致图象是 ;
A. B. C. D.
(2)已知函数:和,若将这两个函数的“差函数”为,判断下列关于“差函数”,描述的正确性,并对正确的描述进行证明:
A.的图象与x轴没有公共点;
B.的图象关于对称;
C.当时,随x的值增大而减小;
D.当时,随着x的值增大,的图象越来越接近的图象,
上述描述正确的为 .
28.(2024八下·秦淮期末)某校开设街舞、唱歌、吉他三项延时活动课程,随机抽取了部分学生对这三项活动课程的兴趣情况进行了调查(每人从中只能选一项),并将调查结果绘制成下面两幅统计图,请你结合图中信息解答问题.
(1)本次抽样调查的样本容量是__________;
(2)将条形统计图补充完整;
(3)已知该校有1200名学生,请你根据样本估计全校学生中喜欢吉他的人数.
29.(2024八下·扬州期末)某车间加工1500个零件后,由于技术革新,工作效率提高到原来的倍,当再加工同样多的零件时,用时比以前少.该车间技术革新前每小时加工多少个零件?
答案解析部分
1.(1),,不等式的解集为或
(2)点E的坐标为或
(3)
2.(1)6
(2)
(3)或
3.(1),
(2)
(3)或
4.(1)
(2)
(3)
5.(1)解:反比例函数经过点,
,
反比例函数解析式为,
点在上,则,
,
把、代入,
得,解得,
一次函数的解析式为;
答:反比例函数解析式为,一次函数的解析式为;
(2)解:把代入,得,
,
,
.
答:的面积为8.
(1)由题意,将代入反比例函数中可得关于m的方程,解方程可求得的值;再将代入反比例函数解析式求得,然后将点、代入一次函数中可得关于k、b的方程组,解方程组求出k、b的值即可;
(2)根据一次函数解析式得出点C,然后根据三角形面积的构成计算即可求解.
6.(1)
(2)①;②且
7.(1)
(2)
8.每个小号垃圾桶的价格是45元
9.(1)k的值为,的值为6
(2)
(3)或
10.(1)①5;②
(2)
11.(1);
(2)的值为或.
(3)
12.(1);
(2);
(3).
13.(1);;
(2)
14.(1)C(9,3),
(2)
(3)存在,(-3,6)或(12,6)或或
15.(1)
(2)①;②
16.(1)
(2)
(3)
17.(1)
(2)
18.(1)点C坐标为或,此时点D坐标为或;
(2)或;
(3)或.
19.(1);
(2)
20.(1),
(2)或
21.(1)100
(2)
(3)72
(4)学生中脊柱侧弯人数占比为,建议学校通过开展脊柱健康知识讲座、举办脊柱保护科普活动等方式,提高学生对于脊柱健康的重视程度, 每天组织学生做护脊操等.让他们养成良好的脊柱保护习惯.(答案不唯一)
22.(1)60,12
(2)
(3)860人
23.(1)5,22
(2)或
24.(1);
(2)或;
(3)或;
(4)或.
25.(1)
(2)
26.(1)①4;②或或1;
(2)
27.(1)①;②D
(2)
28.(1)100
(2)解:选择唱歌的女生人数为:(人),
补全条形统计图如下:
(3)解:(人),
∴全校学生中喜欢吉他的人数约为360人.
(1)解:由图可得,女生总人数为:(人),
男生总人数为:(人),
本次调查的总人数为(人),
即样本容量为100,
故答案为:100.
(1)先分别求出男生和女生的人数,再相加即可;
(2)先求出选择唱歌的女生人数,再作出条形统计图即可;
(3)先求出“ 喜欢吉他 ”的百分比,再乘以1200可得答案.
29.解:设该车间技术革新前每小时加工x个零件,则技术革新后每小时加工个零件,
,
解得:,
经检验,是原分式方程的解;
答:该车间技术革新前每小时加工50个零件.
设该车间技术革新前每小时加工x个零件,则技术革新后每小时加工2.5x个零件,根据工作总量除以工作效率等于工作时间及“提高工作效率后, 再加工同样多的零件时,用时比以前少18h ”建立方程,求解并检验即可.
专项练习 05 解答题
一、解答题
1.(2024八下·南京期末)如图,反比例函数与一次函数的图象交于点、点.
(1)反比例函数为 ,一次函数为 ,不等式的解集为 ;
(2)点E为y轴上一个动点,若,求点E的坐标.
(3)若将一次函数的图像沿y轴向下平移n个单位,使平移后的图像与反比例函数的图像有且只有一个交点,则n的值是 .
2.(2024八下·扬州期末)如图,在平面直角坐标系中,四边形为矩形,点,.动点从点出发,以每秒1个单位长的速度沿射线方向匀速运动,设运动时间为秒.
(1)当______秒时,以、为邻边的平行四边形是菱形;
(2)当点在的垂直平分线上时,求的值;
(3)已知为轴上的一点,若、关于直线对称,求的值.
3.(2024八下·常州期末)如图,一次函数与反比例函数的图像相交于点、.
(1)求一次函数和反比例函数的表达式;
(2)连接、,求的面积;
(3)是轴上的一个动点,过点作直线轴.若与一次函数、反比例函数的图象分别相交于点、,且点在点的上方,则的取值范围是__________.
4.(2024八下·徐州期末)如图,在方格纸中建立平面直角坐标系,与的顶点均为格点.
(1)若绕点逆时针旋转可得到,则旋转角至少为______;
(2)将绕点顺时针旋转得到,画出;
(3)若(2)中的与成中心对称,则对称中心的坐标为______.
5.(2024八下·姑苏期末)如图,一次函数的图象与反比例函数的图象交于,两点,与x轴交于点C.
(1)求一次函数与反比例函数的解析式;
(2)连接,求的面积.
6.(2024八下·海安期末)在平面直角坐标系中,点在直线上.
(1)直线与轴的交点坐标为________;
(2)矩形的顶点分别轴,轴上.
①当,时,求矩形的面积;
②若使矩形的面积为4的点恰好有4个,试求的取值范围.
7.(2024八下·海安期末)为保障旅客快捷、安全的出入车站,海安火车站修建了四个自动检票口,分别记为A、B、C、D.当甲、乙两名乘客通过该站检票口时,请回答下列问题:
(1)甲通过A检票口的概率是________;
(2)用树状图或列表法求甲、乙两名乘客选择不同检票口通过的概率.
8.(2024八下·广陵期末)某中学为配合开展“垃圾分类进校园”活动,新购买了一批不同型号的垃圾分类桶,学校先用4050元购买了一批给班级使用的小号垃圾桶,再用5400元购买了一批放在户外永久使用的大号垃圾桶,已知每个大号垃圾桶的价格是小号垃圾桶的4倍,且购买的数量比小号垃圾桶少60个,求每个小号垃圾桶的价格是多少元?
9.(2024八下·扬州期末)如图,一次函数的图像与反比例函数(,)的图像交于点,与y轴交于点B,与x轴交于点.
(1)求k与m的值;
(2)当时,x的取值范围是________;
(3)若为x轴上的一动点,当的面积为时,求a的值.
10.(2024八下·东台期末)如图,直线轴于点H,且与反比例函数及反比例函数与的图像分别交于点A、B.
(1)若,,连接、.
①的面积为_______;
② 当时,求点B的坐标.
(2)若点,过点A作x轴的平行线,与一次函数的图像交于点D,点D在直线l的左侧,若和变化时,的值始终不变,求对应k的值.
11.(2024八下·惠山期末)如图,平行四边形中,,,点以的速度从点出发沿向点运动,同时点以的速度从点出发沿向点运动,当一个点到达终点时,另一个点也停止运动,设运动的时间为.
(1)求平行四边形的面积;
(2)当的面积为平行四边形的面积的时,求的值;
(3)当时,连接,取线段的中点,请直接写出的长度.
12.(2024八下·惠山期末)如图,在平面直角坐标系中,直线与轴正半轴与轴正半轴分别交于点、,设,(,).将绕点顺时针方向旋转得到,点的对应点为点;再将沿射线方向平移,使点与点重合得到,点的对应点为点,点在轴上,点为线段的中点,点与点恰好落在同一个反比例函数的图象上.
(1)当时,求反比例函数的解析式.
(2)求的值.
(3)若线段、交于点,且的面积为,求的值.
13.(2024八下·姑苏期末)如图,在中,,点A的坐标为,点在反比例函数的图象上.若将线段AB绕点A按顺时针方向旋转90°,得到线段AC,点C恰好在反比例函数的图象上.
(1)求,的值;
(2)若P,Q分别为反比例函数,图象上一点,且以点O,P,Q,A为顶点的四边形为平行四边形,求点P的坐标.
14.(2024八下·苏州工业园期末)如图1,四边形ABCD为正方形,点A在y轴上,点B在x轴上,且OA=6,OB=3,反比例函数在第一象限的图象经过正方形的顶点C.
(1)求点C的坐标和反比例函数的表达式;
(2)如图2,将正方形ABCD沿x轴向右平移m个单位长度得到正方形,点恰好落在反比例函数的图象上,求此时点的坐标;
(3)在(2)的条件下,点P为x轴上一动点,平面内是否存在点Q,使以点O、、P、Q为顶点的四边形为菱形,若存在,请直接写出点Q的坐标,若不存在,请说明理由.
15.(2024八下·吴江期末)在矩形中,,,点是边上的一个动点,,垂足为的延长线交于点.
(1)如图1,延长,若三点在一直线上,,求的长;
(2)过点作,垂足为:
①如图2,若,,求的面积;
②如图3,若,连接,则的值为______.
16.(2024八下·吴江期末)如图,在平面直角坐标系中,已知点,点是线段上的一个动点,过点作轴,交反比例函数的图象于点,过点作的垂线交轴于点,是线段上一点,且,连接,设点的横坐标为.
(1)点的坐标为______;(用含的代数式表示)
(2)若,求点的坐标;
(3)若的面积为3时,点也在反比例函数的图象上,求的值.
17.(2024八下·吴江期末)公元前3世纪,古希腊学者阿基米德发现了著名的“杠杆原理”.杠杆平衡时,阻力阻力臂动力动力臂.几位同学玩撬石头的游戏,已知阻力(石头重量)和阻力臂分别为和.
(1)设动力臂为,动力为,求出与的函数表达式;
(2)若小明使用的力量,他该选择动力臂为多少米的撬棍正好能撬动这块大石头?
18.(2024八下·海门期末)如图,在平面直角坐标系中,直线与x轴,y轴分别交于点A,B,以为边作正方形.
(1)当时,求点C,D的坐标;
(2)当点C的纵坐标为7时,求m的值:
(3)当点C一定不落在第二象限时,直接写出m的取值范围.
19.(2024八下·泰州医药高新技术产业开发期末)如图,在矩形纸片中,E为边上的动点,F为边上的动点,连接.
(1)若.
①如图①,点E与点D重合,点F与点B重合,将矩形纸片沿折叠,点A落在点G处,设与相交于H,求的长;
②如图②,将矩形纸片沿折叠,使点B与点D重合,求折痕的长;
(2)如图③,点E为的中点,点F与点B重合,将矩形纸片沿折叠,点A落在点G处,且点G在矩形内部,延长交于点H,若,求的值.
20.(2024八下·徐州期末)如图,已知一次函数与反比例函数的图象交于点.
(1)求一次函数和反比例函数的表达式;
(2)根据图象,直接写出使成立的自变量的取值范围______.
21.(2024八下·连云港期末)某校学生健康活动中心通过调查,形成了如下调查报告(不完整).
调查目的 1. 为配合卫生部门的“正脊行动”,提前了解全校学生脊柱健康状况 2. 为全校学生保护脊柱健康提出合理建议
调查方式 随机抽样调查 调查对象 本校部分学生
调查内容 该生的脊柱健康状况的检查结果是: A. 正常 B. 轻度侧弯 C. 中度侧弯 D. 重度侧弯
调查结果 学生脊柱健康状况统计表
类型 A B C D 频数(人数) 频率
85 0.85
11 0.11
3 0.03
1 0.01
建议 ……
结合调查信息,回答下列问题:
(1)本次调查共抽查 名学生;
(2)小明用扇形统计图对统计数据进行重新整理,则在小明要画的扇形统计图中,脊柱健康结果为C所对应的扇形圆心角的度数是 °;
(3)若该校共有1800名学生,请估计该校脊柱侧弯程度为中度和重度的总人数是多少?
(4)假如你是学生健康中心成员,请你向该校提一条合理建议.
22.(2024八下·新吴期末)劳动教育是新时代党对教育的新要求,某校为了解学生参加家务劳动的情况,随机抽取了部分学生在某个星期日做家务的时间(单位:)作为样本,将收集的数据整理后分为、、、、五个组别,其中组的数据分别为:0.5,0.4,0.4,0.4,0.3,绘制成如下不完整的统计图表.
各组劳动时间的频数分布表
组别 时间 频数
5
20
15
8
各组劳动时间的扇形统计图
请根据以上信息解答下列问题.
(1)本次调查的样本容量为________,频数分布表中的的值为________;
(2)组所在扇形的圆心角的大小为________;
(3)若该校有1200名学生,估计该校学生劳动时间超过的人数.
23.(2024八下·海陵期末)如图,菱形的顶点A的坐标为,顶点O与坐标原点重合,顶点B在x轴正半轴上,点D是的中点,反比例函数的图像经过点D.
(1)求的长及k的值;
(2)反比例的图像上存在点E,使得的面积为,求点E的坐标.
24.(2024八下·沛县期末)如图,在平面直角坐标系中,正比例函数的图像与反比例函数的图像交于、两点.
(1)求的值;
(2)当时,的取值范围是__________;
(3)当时,的取值范围是__________;
(4)若轴上存在点,使得的面积为,求点的坐标.
25.(2024八下·太仓期末)如图,一次函数的图像与x轴交于点A,与反比例函数的图像交于点,过点B作轴,垂足为点C,点P是反比例函数的图像上的一点,且.
(1)求反比例函数的表达式;
(2)求点P的坐标.
26.(2024八下·太仓期末)如图,四边形是矩形,点P为边上一动点(与点C,D不重合),连接,过点A作交的延长线于点Q,连接,交于点E.设,.
(1)当,时.
①若点P是中点时,求的长;
②若是等腰三角形,求的长;
(2)取的中点M,连接,若在点P运动过程中存在某一位置,使得四边形是平行四边形,则m,n之间的数量关系为______.
27.(2024八下·秦淮期末)对于两个不同的函数,通过减法运算可以得到一个新函数,我们把这个新函数称为两个函数的“差函数”.例如:对于函数和,则函数,的“差函数”记为.
(1)已知函数和,若将这两个函数的“差函数”记为;
①写出的表达式, ;
②函数,的图象如图①所示,则的大致图象是 ;
A. B. C. D.
(2)已知函数:和,若将这两个函数的“差函数”为,判断下列关于“差函数”,描述的正确性,并对正确的描述进行证明:
A.的图象与x轴没有公共点;
B.的图象关于对称;
C.当时,随x的值增大而减小;
D.当时,随着x的值增大,的图象越来越接近的图象,
上述描述正确的为 .
28.(2024八下·秦淮期末)某校开设街舞、唱歌、吉他三项延时活动课程,随机抽取了部分学生对这三项活动课程的兴趣情况进行了调查(每人从中只能选一项),并将调查结果绘制成下面两幅统计图,请你结合图中信息解答问题.
(1)本次抽样调查的样本容量是__________;
(2)将条形统计图补充完整;
(3)已知该校有1200名学生,请你根据样本估计全校学生中喜欢吉他的人数.
29.(2024八下·扬州期末)某车间加工1500个零件后,由于技术革新,工作效率提高到原来的倍,当再加工同样多的零件时,用时比以前少.该车间技术革新前每小时加工多少个零件?
答案解析部分
1.(1),,不等式的解集为或
(2)点E的坐标为或
(3)
2.(1)6
(2)
(3)或
3.(1),
(2)
(3)或
4.(1)
(2)
(3)
5.(1)解:反比例函数经过点,
,
反比例函数解析式为,
点在上,则,
,
把、代入,
得,解得,
一次函数的解析式为;
答:反比例函数解析式为,一次函数的解析式为;
(2)解:把代入,得,
,
,
.
答:的面积为8.
(1)由题意,将代入反比例函数中可得关于m的方程,解方程可求得的值;再将代入反比例函数解析式求得,然后将点、代入一次函数中可得关于k、b的方程组,解方程组求出k、b的值即可;
(2)根据一次函数解析式得出点C,然后根据三角形面积的构成计算即可求解.
6.(1)
(2)①;②且
7.(1)
(2)
8.每个小号垃圾桶的价格是45元
9.(1)k的值为,的值为6
(2)
(3)或
10.(1)①5;②
(2)
11.(1);
(2)的值为或.
(3)
12.(1);
(2);
(3).
13.(1);;
(2)
14.(1)C(9,3),
(2)
(3)存在,(-3,6)或(12,6)或或
15.(1)
(2)①;②
16.(1)
(2)
(3)
17.(1)
(2)
18.(1)点C坐标为或,此时点D坐标为或;
(2)或;
(3)或.
19.(1);
(2)
20.(1),
(2)或
21.(1)100
(2)
(3)72
(4)学生中脊柱侧弯人数占比为,建议学校通过开展脊柱健康知识讲座、举办脊柱保护科普活动等方式,提高学生对于脊柱健康的重视程度, 每天组织学生做护脊操等.让他们养成良好的脊柱保护习惯.(答案不唯一)
22.(1)60,12
(2)
(3)860人
23.(1)5,22
(2)或
24.(1);
(2)或;
(3)或;
(4)或.
25.(1)
(2)
26.(1)①4;②或或1;
(2)
27.(1)①;②D
(2)
28.(1)100
(2)解:选择唱歌的女生人数为:(人),
补全条形统计图如下:
(3)解:(人),
∴全校学生中喜欢吉他的人数约为360人.
(1)解:由图可得,女生总人数为:(人),
男生总人数为:(人),
本次调查的总人数为(人),
即样本容量为100,
故答案为:100.
(1)先分别求出男生和女生的人数,再相加即可;
(2)先求出选择唱歌的女生人数,再作出条形统计图即可;
(3)先求出“ 喜欢吉他 ”的百分比,再乘以1200可得答案.
29.解:设该车间技术革新前每小时加工x个零件,则技术革新后每小时加工个零件,
,
解得:,
经检验,是原分式方程的解;
答:该车间技术革新前每小时加工50个零件.
设该车间技术革新前每小时加工x个零件,则技术革新后每小时加工2.5x个零件,根据工作总量除以工作效率等于工作时间及“提高工作效率后, 再加工同样多的零件时,用时比以前少18h ”建立方程,求解并检验即可.
同课章节目录
