【期末押题预测】运动的合成与分解(含解析)2024-2025学年高中物理教科版(2019)高一下册
文档属性
| 名称 | 【期末押题预测】运动的合成与分解(含解析)2024-2025学年高中物理教科版(2019)高一下册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-05-27 07:46:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末押题预测 运动的合成与分解
一.选择题(共5小题)
1.(2024秋 沙坪坝区校级期末)下列不共线的两个分运动,其合运动轨迹一定是曲线的是( )
A.两个匀速直线运动
B.一个匀速直线运动和一个匀变速直线运动
C.两个匀变速直线运动
D.两个初速度不为零的匀变速直线运动
2.(2024秋 沙坪坝区校级期末)如图所示,一质点在恒力作用下做曲线运动,从M点运动到N点过程中,质点的速度方向恰好改变了90°,且vM:vN=1:1,下列说法正确的是( )
A.质点从M点到N点的过程中做匀速曲线运动
B.质点在M点受力竖直向下,N点受力水平向右
C.质点从M点到N点的过程中速度先减小后增大
D.质点从M点到N点的过程中受力与水平方向成37°
3.(2024秋 碑林区校级期末)如图所示,光滑水平面上固定两个光滑立柱A和B,两根柔软轻绳对称地跨过两立柱,每根绳的一端系在物体上的O点,另一端施加沿绳方向的等大外力,使物体能沿两绳夹角的角平分线运动,物体质量为m。当绳子之间夹角为2α瞬间,绳端速度大小为v,拉力大小为F,此时物体的速度v物和加速度a物表达式正确的是( )
A. B.v物=2vcosα
C. D.
4.(2024秋 鼓楼区校级期末)某小组通过实验得到了物体在恒定合外力作用下的一条运动轨迹OP曲线,如图所示。以下对该运动给出的几种推理正确的是( )
A.该物体的运动轨迹一定为抛物线
B.该运动可分解为沿x轴方向匀速直线运动和沿y轴方向匀速直线运动
C.该运动一定可分解为沿x轴方向匀加速直线运动和沿y轴方向匀加速直线运动
D.若该物体沿x轴方向为匀速直线运动,则物体所受合力不一定平行于y轴
5.(2024秋 鼓楼区校级期末)物块B套在倾斜杆上,并用轻绳与物块A相连,今对B施加一个力F(未画出)使物块B沿杆由点M匀速下滑到N点,运动中连接A、B的轻绳始终保持绷紧状态,在下滑过程中,下列说法正确的是( )
A.物块A的速度先变大后变小
B.物块A的速度先变小后变大
C.物块A先处于超重状态,后处于失重状态
D.物块A先处于失重状态,后处于超重状态
二.多选题(共4小题)
(多选)6.(2024秋 邯郸期末)光滑水平面上建立直角坐标系,质量为m的小球(可视为质点),从y轴上的B点(0,L)以初速度水平向右进入第一象限,经一段时间过x轴上的C点(L,0)时速度大小为。此过程始终受一个平行于xOy平面但方向大小未知的恒力。则( )
A.小球在沿x轴方向上做匀速直线运动
B.小球从B到C的时间为
C.小球所受恒力大小为
D.小球过C点时速度方向与x轴正向夹角为60°
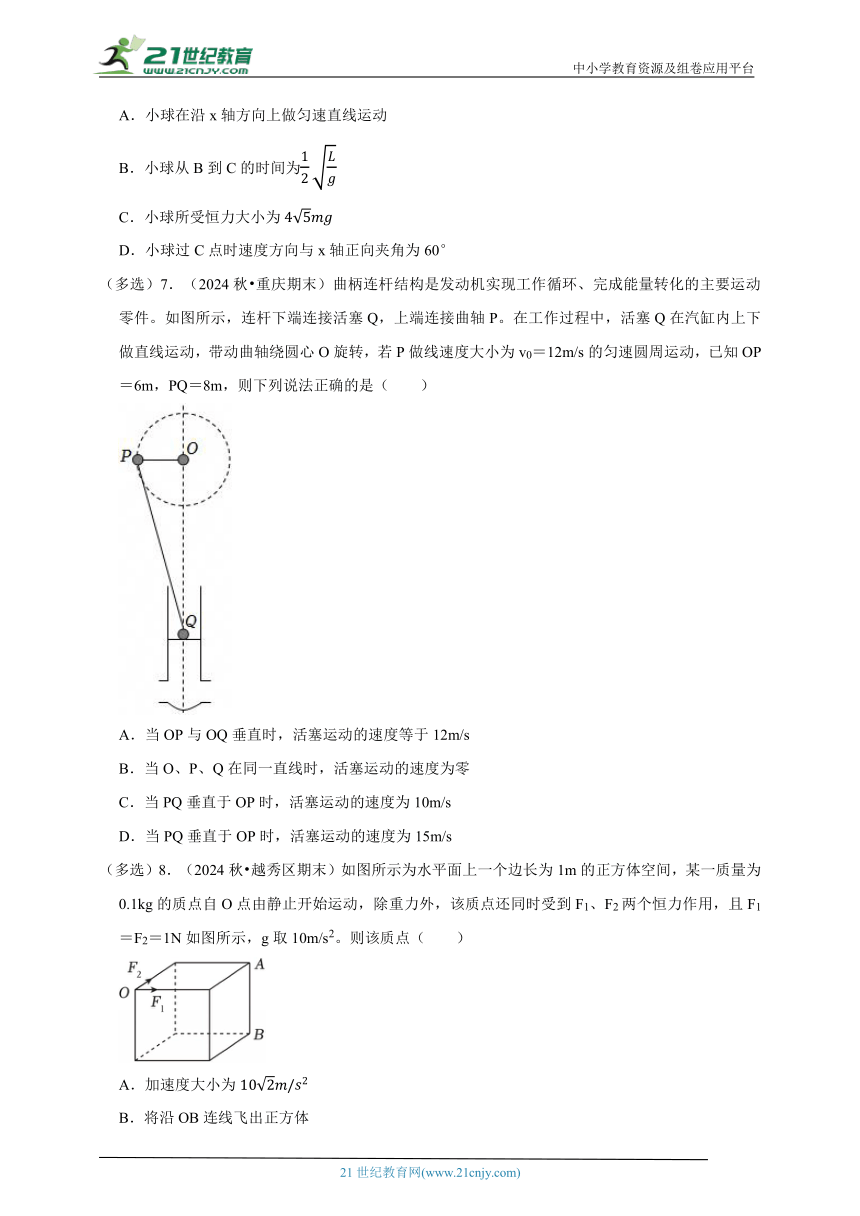
(多选)7.(2024秋 重庆期末)曲柄连杆结构是发动机实现工作循环、完成能量转化的主要运动零件。如图所示,连杆下端连接活塞Q,上端连接曲轴P。在工作过程中,活塞Q在汽缸内上下做直线运动,带动曲轴绕圆心O旋转,若P做线速度大小为v0=12m/s的匀速圆周运动,已知OP=6m,PQ=8m,则下列说法正确的是( )
A.当OP与OQ垂直时,活塞运动的速度等于12m/s
B.当O、P、Q在同一直线时,活塞运动的速度为零
C.当PQ垂直于OP时,活塞运动的速度为10m/s
D.当PQ垂直于OP时,活塞运动的速度为15m/s
(多选)8.(2024秋 越秀区期末)如图所示为水平面上一个边长为1m的正方体空间,某一质量为0.1kg的质点自O点由静止开始运动,除重力外,该质点还同时受到F1、F2两个恒力作用,且F1=F2=1N如图所示,g取10m/s2。则该质点( )
A.加速度大小为
B.将沿OB连线飞出正方体
C.在正方体区域内运动时间为1s
D.在正方体区域内运动时间为
(多选)9.(2024秋 武汉期末)如图所示,轻杆AB的中点固定着小球C,现使A端不脱离墙面,B端在水平面上以v向右匀速运动。当杆与水平面成α角时,下列说法正确的是( )
A.杆上A端的速度大小为
B.小球C的速度大小为
C.杆对小球C的作用力方向一定沿竖直方向
D.杆对小球C的作用力方向一定沿杆方向
三.填空题(共3小题)
10.(2024秋 黄浦区校级期末)一渡船在宽为d的河中航行。现从码头出发,船头垂直于河岸,以速度v匀速驶向对岸,则渡河时间为 ;若越靠近河中央水流速度u越大,则渡船行驶的轨迹示意图为如图的 (选填“甲”或“乙”)。
11.(2024秋 普陀区校级期末)移动射靶的简化情景如图所示,靶沿水平轨道快速横向移动,射手站定不动,用步枪向靶射击。设靶移动的速度大小为v0,子弹出射速度的大小为v,移动靶离射手的最近距离为d。则子弹射中目标的最短时间为 ,此种情况下,射手射击时,枪口离目标的距离为 。
12.(2023秋 嘉定区校级期末)渡过一宽100m的河,船相对静水速度5m/s,水流速度3m/s,则过河最短时间为 s.如果第二天过河的过程中突发暴雨,水流加快,则过河最短时间 (不变、变大、变小)。
四.解答题(共3小题)
13.(2024秋 辽宁期末)2024年11月12日,第十五届中国国际航空航天博览会在珠海开幕,本届航展期间,“飞行汽车”是最火的展台,打“飞的”去远方或许不久就能实现。一辆飞行汽车在表演时在平直的公路上以20m/s的速度行驶,某时刻驾驶员启动飞行模式,汽车保持水平速度不变,沿竖直方向开始匀加速爬升,经过一段时间爬升到100m高处,用x表示水平位移,y表示竖直位移,这一过程的y﹣x图像如图所示。求汽车飞行时:
(1)从启动飞行模式,到离地100m高处需要多长时间;
(2)到达100m高处时竖直速度和瞬时速度的大小。
14.(2024秋 黄浦区校级期末)一质点在光滑水平面上运动,它的x方向和y方向的两个分速度—时间图像分别如图甲和图乙所示。
(1)可判断质点运动性质为做 (选填“匀变速”或“变加速”) (选填“直线”或“曲线”)运动;
(2)4s时速度v与x轴正方向的夹角为 °;
(3)质点在4s内的位移s大小为 m,请在图丙中大致画出质点的运动轨迹图。
15.(2024秋 城关区校级期末)如图所示,一探险者正从某瀑布上游划船渡河,已知河流的宽度d=200m,此时探险者正处于河流正中央A点处,该点与下游瀑布危险区的最短距离为。已知水流速度为v1=4m/s(sin37°=0.6,cos37°=0.8)。从此时开始计时,
(1)若小船在静水中速度为v2=5m/s,则船到岸的最短时间是多少?所到目的地与河流正对岸间的距离是多少?
(2)若小船在静水中速度为v2=5m/s,则小船以最短的距离到岸时所需时间是多少?此时船头方向与河岸上游的夹角是多少?
(3)为了使小船能避开危险区沿直线到达对岸,小船在静水中的速度至少是多少?
期末押题预测 运动的合成与分解
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 沙坪坝区校级期末)下列不共线的两个分运动,其合运动轨迹一定是曲线的是( )
A.两个匀速直线运动
B.一个匀速直线运动和一个匀变速直线运动
C.两个匀变速直线运动
D.两个初速度不为零的匀变速直线运动
【考点】分析合运动的轨迹问题;合运动与分运动的关系.
【专题】定性思想;推理法;物体做曲线运动条件专题;理解能力.
【答案】B
【分析】当物体所受的合外力和它速度方向不在同一直线上,物体就是在做曲线运动,即速度方向与加速度方向不同时,物体做曲线运动。
【解答】解:A、两个匀速直线运动的合运动是匀速直线运动,故A错误;
CD、两个分运动的合运动的方向与加速度可能在同一直线,故可能做直线运动,故CD错误;
B、合运动方向与加速度方向一定不再同一直线,故合运动轨迹一定是曲线,故B正确。
故选:B。
【点评】考查对物体做曲线运动条件的理解,熟悉其定义。
2.(2024秋 沙坪坝区校级期末)如图所示,一质点在恒力作用下做曲线运动,从M点运动到N点过程中,质点的速度方向恰好改变了90°,且vM:vN=1:1,下列说法正确的是( )
A.质点从M点到N点的过程中做匀速曲线运动
B.质点在M点受力竖直向下,N点受力水平向右
C.质点从M点到N点的过程中速度先减小后增大
D.质点从M点到N点的过程中受力与水平方向成37°
【考点】一个匀速直线和一个变速直线运动的合成;物体运动轨迹、速度、受力(加速度)的相互判断.
【专题】应用题;定量思想;推理法;运动的合成和分解专题;分析综合能力.
【答案】C
【分析】把质点的运动分解为沿MO方向与ON方向的分运动,应用运动学公式分析答题。
【解答】解:A、质点在恒力作用下运动,质点所受合力不变,加速度不变,质点做匀变速曲线运动,故A错误;
BD、质点沿MO方向做匀减速直线运动且末速度为零,在ON方向做初速度为零的匀加速直线运动,由题意可知:vM:vN=1:1,则质点在MO方向与ON方向的加速度大小相等,在这两个方向所受合力大小相等,质点所受恒力方向与ON方向间夹角的正切值tanθ1,则θ=45°,质点所受合力方向不变,故BD错误;
C、质点从M点到N点过程,速度方向与恒力方向的夹角由钝角变为直角再变为锐角,质点先做减速运动后做加速运动,质点的速度先减小再增大,故C正确。
故选:C。
【点评】根据质点的运动过程,应用运动的合成与分解、运动学规律即可解题。
3.(2024秋 碑林区校级期末)如图所示,光滑水平面上固定两个光滑立柱A和B,两根柔软轻绳对称地跨过两立柱,每根绳的一端系在物体上的O点,另一端施加沿绳方向的等大外力,使物体能沿两绳夹角的角平分线运动,物体质量为m。当绳子之间夹角为2α瞬间,绳端速度大小为v,拉力大小为F,此时物体的速度v物和加速度a物表达式正确的是( )
A. B.v物=2vcosα
C. D.
【考点】关联速度问题;力的合成与分解的应用;牛顿第二定律的简单应用.
【专题】定量思想;合成分解法;运动的合成和分解专题;牛顿运动定律综合专题;推理论证能力.
【答案】D
【分析】把物体的速度分解为沿绳方向和垂直于绳的方向,然后根据矢量法则计算物体的速度;根据牛顿第二定律计算物体的加速度。
【解答】解:AB、把物体的速度分解为沿绳方向和垂直于绳的方向,对左边的绳子来说,画出物体的速度分解图像,如图所示
则v物,故AB错误;
CD、根据牛顿第二定律有2Fcosα=ma物,解得a物,故C错误,D正确。
故选:D。
【点评】知道把物体的速度分解为沿绳方向和垂直于绳的方向是解题的基础。
4.(2024秋 鼓楼区校级期末)某小组通过实验得到了物体在恒定合外力作用下的一条运动轨迹OP曲线,如图所示。以下对该运动给出的几种推理正确的是( )
A.该物体的运动轨迹一定为抛物线
B.该运动可分解为沿x轴方向匀速直线运动和沿y轴方向匀速直线运动
C.该运动一定可分解为沿x轴方向匀加速直线运动和沿y轴方向匀加速直线运动
D.若该物体沿x轴方向为匀速直线运动,则物体所受合力不一定平行于y轴
【考点】合运动与分运动的关系;物体做曲线运动的条件;物体运动轨迹、速度、受力(加速度)的相互判断.
【专题】定性思想;推理法;物体做曲线运动条件专题;理解能力.
【答案】A
【分析】当物体所受合外力的方向与它的速度方向不在同一直线上时,物体就会做曲线运动。
【解答】解:A.恒力表示大小和方向都不变的力,物体加速度方向恒定,但与初速度方向不同,它的运动轨迹就是抛物线.,故A正确;
B.若两个运动都是匀速直线运动,则物体受到的合力为零,不可能做曲线运动,故B错误;
C.若两个方向都做匀加速直线运动,则合力指向第一象限,则不可能像x轴方向弯曲,故C错误;
D.合力指向轨迹的内侧,所以y轴方向为匀速直线运动,则物体所受合力一定指向x轴正方向,故D错误。
故选:A。
【点评】考查对物体做曲线运动条件的理解,熟悉其定义。
5.(2024秋 鼓楼区校级期末)物块B套在倾斜杆上,并用轻绳与物块A相连,今对B施加一个力F(未画出)使物块B沿杆由点M匀速下滑到N点,运动中连接A、B的轻绳始终保持绷紧状态,在下滑过程中,下列说法正确的是( )
A.物块A的速度先变大后变小
B.物块A的速度先变小后变大
C.物块A先处于超重状态,后处于失重状态
D.物块A先处于失重状态,后处于超重状态
【考点】关联速度问题;牛顿第二定律求解多过程问题;超重与失重的概念、特点和判断.
【专题】定量思想;合成分解法;运动的合成和分解专题;推理论证能力.
【答案】B
【分析】把B物体的速度分解为沿绳方向和垂直绳的方向,根据平行四边形定则分析即可;根据加速度方向分析。
【解答】解:把B物体的速度分解为沿绳方向和垂直绳的方向,如图所示
AB、根据平行四边形形定则,沿绳子方向的速度为vA=vBcosθ,θ指绳与杆之间的夹角,所以cosθ先减小后增大,故物块A的速度先变小后变大,故A错误,B正确。
CD、物体A先向下做减速运动,后向上做加速运动,加速度的方向始终向上,所以A始终处于超重状态。故CD错误。
故选:B。
【点评】解决本题的关键是要知道A沿绳子方向上的分速度等于B的速度,以及知道超重状态时物体的加速度的方向向上,失重状态时加道向下即可。
二.多选题(共4小题)
(多选)6.(2024秋 邯郸期末)光滑水平面上建立直角坐标系,质量为m的小球(可视为质点),从y轴上的B点(0,L)以初速度水平向右进入第一象限,经一段时间过x轴上的C点(L,0)时速度大小为。此过程始终受一个平行于xOy平面但方向大小未知的恒力。则( )
A.小球在沿x轴方向上做匀速直线运动
B.小球从B到C的时间为
C.小球所受恒力大小为
D.小球过C点时速度方向与x轴正向夹角为60°
【考点】一个匀速直线和一个变速直线运动的合成;牛顿第二定律的简单应用.
【专题】定量思想;推理法;运动的合成和分解专题;推理论证能力.
【答案】BC
【分析】将恒力沿水平方向以及竖直方向分解,在各个方向上分别利用牛顿运动定律以及运动学公式分析。
【解答】解:ABD.设第一象限恒力的水平分量为Fx,竖直分量为Fy,则
Fx=max
Fy=may
设小球在C点的水平分速度为vx,竖直分速度为vy,速度方向与x轴正向夹角为θ,则
且
解得
,,,θ=53°
故AD错误,B正确;
C.x方向有
可得
Fx=max=4mgy方向有
解得
Fy=may=8mg
则可得
故C正确。
故选:BC。
【点评】运动分解时,各个分运动彼此相互独立,具有等时性。
(多选)7.(2024秋 重庆期末)曲柄连杆结构是发动机实现工作循环、完成能量转化的主要运动零件。如图所示,连杆下端连接活塞Q,上端连接曲轴P。在工作过程中,活塞Q在汽缸内上下做直线运动,带动曲轴绕圆心O旋转,若P做线速度大小为v0=12m/s的匀速圆周运动,已知OP=6m,PQ=8m,则下列说法正确的是( )
A.当OP与OQ垂直时,活塞运动的速度等于12m/s
B.当O、P、Q在同一直线时,活塞运动的速度为零
C.当PQ垂直于OP时,活塞运动的速度为10m/s
D.当PQ垂直于OP时,活塞运动的速度为15m/s
【考点】关联速度问题.
【专题】定量思想;合成分解法;运动的合成和分解专题;推理论证能力.
【答案】ABD
【分析】Q点做直线运动,而P点做匀速圆周运动,将P在两个特殊点的速度分解即可作出判断。
【解答】解:对P和Q的运动分解,如图所示
由关联速度可知vPcosα=vQcosβ,则
A、当OP与OQ垂直时,α=β,P点速度的大小为v0,此时杆PQ整体运动的方向是相同的,方向沿OQ的平行的方向,所以活塞运动的速度等于P点的速度,都是v0=12m/s,故A正确;
B、当O、P、Q在同一直线时,P点的速度方向与OQ方向垂直,沿OQ方向的分速度为0,Q的瞬时速度为0,所以活塞运动的速度等于0,故B正确;
CD、当PQ垂直于OP时,即杆与圆相切,,根据几何关系可得,解得vQ=15m/s,故C错误,D正确。
故选:ABD。
【点评】曲柄连杆结构是发动机的联动速度传送较为复杂,但该题中的两个特殊点的速度关系是比较明显的,要正确理解它们之间的关系。
(多选)8.(2024秋 越秀区期末)如图所示为水平面上一个边长为1m的正方体空间,某一质量为0.1kg的质点自O点由静止开始运动,除重力外,该质点还同时受到F1、F2两个恒力作用,且F1=F2=1N如图所示,g取10m/s2。则该质点( )
A.加速度大小为
B.将沿OB连线飞出正方体
C.在正方体区域内运动时间为1s
D.在正方体区域内运动时间为
【考点】两个变速直线运动的合成.
【专题】定量思想;合成分解法;运动的合成和分解专题;推理论证能力.
【答案】BD
【分析】根据力的合成法则得到质点所受合力大小,然后根据牛顿第二定律得到加速度大小,根据合力方向分析质点的运动方向;根据运动学公式计算质点在正方体区域的运动时间。
【解答】解:AB、根据力的合成法则可知,质点所受合力大小为FN,方向与竖直方向的正切值为,即方向沿OB连线,根据牛顿第二定律可得质点的加速度大小为a,因为质点是从静止出发的,所以质点的运动方向沿OB方向,故A错误,B正确;
CD、因为F1=F2=1N,都等于重力mg,质点沿F1、F2方向的加速度大小都等于重力加速度,则根据l可得质点在正方体区域内的运动时间为:t,故C错误,D正确。
故选:BD。
【点评】掌握力的合成法则是解题的关键,知道把质点的运动分解为力的方向,根据运动学公式计算时间。
(多选)9.(2024秋 武汉期末)如图所示,轻杆AB的中点固定着小球C,现使A端不脱离墙面,B端在水平面上以v向右匀速运动。当杆与水平面成α角时,下列说法正确的是( )
A.杆上A端的速度大小为
B.小球C的速度大小为
C.杆对小球C的作用力方向一定沿竖直方向
D.杆对小球C的作用力方向一定沿杆方向
【考点】关联速度问题.
【专题】定量思想;合成分解法;运动的合成和分解专题;推理论证能力.
【答案】AC
【分析】分解A、B两点的速度,根据它们沿杆方向的速度相等分析;C既有水平方向的速度,也有竖直方向的速度,根据速度矢量合成法则计算;根据C球在水平方向做匀速直线运动,竖直方向做变速运动分析小球C的受力。
【解答】解:A、分解A、B两点的速度,如图所示
则vcosα=vAsinα,解得,故A正确;
B、以墙角为坐标原点,设C点横、纵坐标分别为x、y,杆长为L,则A点纵坐标为2y,B点横坐标为2x,则有(2x)2+(2y)2=L2,可得C点的轨迹方程为,即轨迹为圆,其速率满足,代入数据得 ,故B错误;
CD、C点的水平分速度为B速度的一半,所以C在水平方向上匀速运动,水平方向合力为0,竖直方向变速运动,所以杆对小球C的作用力方向一定沿竖直方向,故C正确,D错误。
故选:AC。
【点评】A、B两端点沿杆方向的分速度相等,C点的水平分速度为B速度的一半,竖直分速度为A的一半,这两点是本题的解题关键。
三.填空题(共3小题)
10.(2024秋 黄浦区校级期末)一渡船在宽为d的河中航行。现从码头出发,船头垂直于河岸,以速度v匀速驶向对岸,则渡河时间为 ;若越靠近河中央水流速度u越大,则渡船行驶的轨迹示意图为如图的 甲 (选填“甲”或“乙”)。
【考点】小船过河问题.
【专题】定量思想;推理法;运动的合成和分解专题;理解能力.
【答案】;甲。
【分析】根据宽度和速度求解时间;根据速度的变化情况分析。
【解答】解:渡船在垂直河岸的方向以速度v匀速向对岸行驶,设渡河时间为t,则有;设合速度方向与河岸方向夹角为θ,则有,若越靠近河中央水的流速越大,即水速u先增大后减小,则沿着河岸方向先加速后减速,而垂直河岸方向为匀速直线运动,则tanθ先减小后增大,即θ先减小和增大,曲线运动速度的方向沿切线方向,则轨迹如图甲。
故答案为:;甲。
【点评】考查对合运动与分运动的关系,属于基础知识。
11.(2024秋 普陀区校级期末)移动射靶的简化情景如图所示,靶沿水平轨道快速横向移动,射手站定不动,用步枪向靶射击。设靶移动的速度大小为v0,子弹出射速度的大小为v,移动靶离射手的最近距离为d。则子弹射中目标的最短时间为 ,此种情况下,射手射击时,枪口离目标的距离为 。
【考点】小船过河问题.
【专题】定量思想;推理法;运动的合成和分解专题;推理论证能力.
【答案】;。
【分析】当子弹垂直轨道运动时,射中目标的位移最小,时间最短。根据最短时间计算移动靶的位移,运用合成法求解距离。
【解答】解:子弹垂直轨道运动时,射中目标的时间最短,为,此种情况下,射手射击时,枪口离目标的距离为。
故答案为:;。
【点评】考查对运动的合成与分解的理解,熟悉和运动与分运动的关联。
12.(2023秋 嘉定区校级期末)渡过一宽100m的河,船相对静水速度5m/s,水流速度3m/s,则过河最短时间为 20 s.如果第二天过河的过程中突发暴雨,水流加快,则过河最短时间 不变 (不变、变大、变小)。
【考点】合运动与分运动的关系.
【专题】定量思想;推理法;运动的合成和分解专题;推理论证能力.
【答案】20;不变。
【分析】将船的运动分解成垂直、平行河岸两个方向,船头垂直于河岸航行时所用时间最短。
【解答】解:船头垂直于河岸航行时所用时间最短,此种情况渡河时间为,过河的时间与河水的流速无关,水流加快时,过河时间不变。
故答案为:20;不变。
【点评】考查对运动的合成与分解的理解,将船的运动分解成垂直、平行河岸两个方向,分析垂直方向的运动即可。
四.解答题(共3小题)
13.(2024秋 辽宁期末)2024年11月12日,第十五届中国国际航空航天博览会在珠海开幕,本届航展期间,“飞行汽车”是最火的展台,打“飞的”去远方或许不久就能实现。一辆飞行汽车在表演时在平直的公路上以20m/s的速度行驶,某时刻驾驶员启动飞行模式,汽车保持水平速度不变,沿竖直方向开始匀加速爬升,经过一段时间爬升到100m高处,用x表示水平位移,y表示竖直位移,这一过程的y﹣x图像如图所示。求汽车飞行时:
(1)从启动飞行模式,到离地100m高处需要多长时间;
(2)到达100m高处时竖直速度和瞬时速度的大小。
【考点】一个匀速直线和一个变速直线运动的合成;匀变速直线运动规律的综合应用.
【专题】定量思想;方程法;直线运动规律专题;理解能力.
【答案】(1)从启动飞行模式,到离地100m高处需要10s;
(2)到达100m高处时竖直速度为20m/s,瞬时速度的大小为。
【分析】(1)根据水平方向速度与位移求解时间;
(2)根据匀变速直线运动推论求解竖直速度,根据分速度求解合速度。
【解答】解:(1)飞行汽车的水平速度不变,当爬升到100m高处时有x=v0t,解得t10s;
(2)竖直方向做匀加速直线运动,有,解得;
合速度为。
答:(1)从启动飞行模式,到离地100m高处需要10s;
(2)到达100m高处时竖直速度为20m/s,瞬时速度的大小为。
【点评】考查对匀变速直线运动规律的理解和分速度与合速度的关系,熟悉运动学公式的运用。
14.(2024秋 黄浦区校级期末)一质点在光滑水平面上运动,它的x方向和y方向的两个分速度—时间图像分别如图甲和图乙所示。
(1)可判断质点运动性质为做 匀变速 (选填“匀变速”或“变加速”) 曲线 (选填“直线”或“曲线”)运动;
(2)4s时速度v与x轴正方向的夹角为 37 °;
(3)质点在4s内的位移s大小为 16 m,请在图丙中大致画出质点的运动轨迹图。
【考点】运动的合成与分解的图像类问题;一个匀速直线和一个变速直线运动的合成.
【专题】定量思想;推理法;运动学中的图象专题;理解能力.
【答案】(1)匀变速,曲线;
(2)37;
(3)16,。
【分析】v﹣t图像反映了做直线运动的物体的速度随时间变化的规律,斜率表示加速度的大小及方向,图线与时间轴所包围的“面积”表示位移。
【解答】解:(1)由图可知,该质点沿x方向做匀速直线运动,沿y方向做匀变速直线运动,0~2s内y方向速度匀速减小,2~4s内y方向速度匀速增大,可知合力的方向沿y方向,与和速度方向不一致,故质点做曲线运动;
(2)4s时速度vx=4m/s,vy=﹣3m/s,设与x轴正方向的夹角为θ,根据几何关系得,解得θ=37°;
(3)v﹣t图像与时间轴所包围的“面积”表示位移,可得4s内x轴方向的位移为xx=4×4m=16m,y轴方向的位移为,y轴方向的最大位移为,质点在4s内的位移s大小为16m,质点的运动轨迹如图
。
故答案为:(1)匀变速,曲线;
(2)37;
(3)16,。
【点评】考查对v﹣t图像的理解,清楚图线的含义。
15.(2024秋 城关区校级期末)如图所示,一探险者正从某瀑布上游划船渡河,已知河流的宽度d=200m,此时探险者正处于河流正中央A点处,该点与下游瀑布危险区的最短距离为。已知水流速度为v1=4m/s(sin37°=0.6,cos37°=0.8)。从此时开始计时,
(1)若小船在静水中速度为v2=5m/s,则船到岸的最短时间是多少?所到目的地与河流正对岸间的距离是多少?
(2)若小船在静水中速度为v2=5m/s,则小船以最短的距离到岸时所需时间是多少?此时船头方向与河岸上游的夹角是多少?
(3)为了使小船能避开危险区沿直线到达对岸,小船在静水中的速度至少是多少?
【考点】小船过河问题;合运动与分运动的关系.
【专题】计算题;定量思想;推理法;运动的合成和分解专题;推理论证能力.
【答案】(1)船到岸的最短时间是20s,所到目的地与河流正对岸间的距离是80m。
(2)小船以最短的距离到岸时所需时间是,此时船头方向与河岸上游的夹角是37°;
(3)为了使小船能避开危险区沿直线到达对岸,小船在静水中的速度至少是2m/s。
【分析】(1)根据船头方向垂直河岸时,则渡河时间最短,结合运动学公式,即可求解;
(2)当船的合速度垂直河岸时,渡河的位移最小,结合三角知识,及运动学公式,即可求解;
(3)当小船在静水中的速度与合速度垂直时,借助于平行四边形定则,即可求出小船在静水中最小速度。
【解答】解:(1)当船头方向垂直河岸时,则渡河时间最短,则最短时间为t,解得t20s;
所到目的地与河流正对岸间的距离x=v1t,解得x=4×20m=80m;
(2)设船头与河岸的夹角为θ,如图
由图知,解得θ=37°
船的合速度,
渡河时间;
(3)小船避开危险区沿直线到达对岸,合速度与水流速度的夹角为α,即有,则α=30°
小船在河水中运动时,当小船在静水中的速度与合速度垂直时,小船在静水中的速度最小为vmin=v1sinα=4×sin30°m/s=2m/s。
答:(1)船到岸的最短时间是20s,所到目的地与河流正对岸间的距离是80m。
(2)小船以最短的距离到岸时所需时间是,此时船头方向与河岸上游的夹角是37°;
(3)为了使小船能避开危险区沿直线到达对岸,小船在静水中的速度至少是2m/s。
【点评】本题属于:一个速度要分解,已知一个分速度的大小与方向,还已知另一个分速度的大小且最小,则求这个分速度的方向与大小值;这种题型运用平行四边形定则,由几何关系来确定最小值;同时掌握渡河时间最短,与渡河位移最小的求解方法。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末押题预测 运动的合成与分解
一.选择题(共5小题)
1.(2024秋 沙坪坝区校级期末)下列不共线的两个分运动,其合运动轨迹一定是曲线的是( )
A.两个匀速直线运动
B.一个匀速直线运动和一个匀变速直线运动
C.两个匀变速直线运动
D.两个初速度不为零的匀变速直线运动
2.(2024秋 沙坪坝区校级期末)如图所示,一质点在恒力作用下做曲线运动,从M点运动到N点过程中,质点的速度方向恰好改变了90°,且vM:vN=1:1,下列说法正确的是( )
A.质点从M点到N点的过程中做匀速曲线运动
B.质点在M点受力竖直向下,N点受力水平向右
C.质点从M点到N点的过程中速度先减小后增大
D.质点从M点到N点的过程中受力与水平方向成37°
3.(2024秋 碑林区校级期末)如图所示,光滑水平面上固定两个光滑立柱A和B,两根柔软轻绳对称地跨过两立柱,每根绳的一端系在物体上的O点,另一端施加沿绳方向的等大外力,使物体能沿两绳夹角的角平分线运动,物体质量为m。当绳子之间夹角为2α瞬间,绳端速度大小为v,拉力大小为F,此时物体的速度v物和加速度a物表达式正确的是( )
A. B.v物=2vcosα
C. D.
4.(2024秋 鼓楼区校级期末)某小组通过实验得到了物体在恒定合外力作用下的一条运动轨迹OP曲线,如图所示。以下对该运动给出的几种推理正确的是( )
A.该物体的运动轨迹一定为抛物线
B.该运动可分解为沿x轴方向匀速直线运动和沿y轴方向匀速直线运动
C.该运动一定可分解为沿x轴方向匀加速直线运动和沿y轴方向匀加速直线运动
D.若该物体沿x轴方向为匀速直线运动,则物体所受合力不一定平行于y轴
5.(2024秋 鼓楼区校级期末)物块B套在倾斜杆上,并用轻绳与物块A相连,今对B施加一个力F(未画出)使物块B沿杆由点M匀速下滑到N点,运动中连接A、B的轻绳始终保持绷紧状态,在下滑过程中,下列说法正确的是( )
A.物块A的速度先变大后变小
B.物块A的速度先变小后变大
C.物块A先处于超重状态,后处于失重状态
D.物块A先处于失重状态,后处于超重状态
二.多选题(共4小题)
(多选)6.(2024秋 邯郸期末)光滑水平面上建立直角坐标系,质量为m的小球(可视为质点),从y轴上的B点(0,L)以初速度水平向右进入第一象限,经一段时间过x轴上的C点(L,0)时速度大小为。此过程始终受一个平行于xOy平面但方向大小未知的恒力。则( )
A.小球在沿x轴方向上做匀速直线运动
B.小球从B到C的时间为
C.小球所受恒力大小为
D.小球过C点时速度方向与x轴正向夹角为60°
(多选)7.(2024秋 重庆期末)曲柄连杆结构是发动机实现工作循环、完成能量转化的主要运动零件。如图所示,连杆下端连接活塞Q,上端连接曲轴P。在工作过程中,活塞Q在汽缸内上下做直线运动,带动曲轴绕圆心O旋转,若P做线速度大小为v0=12m/s的匀速圆周运动,已知OP=6m,PQ=8m,则下列说法正确的是( )
A.当OP与OQ垂直时,活塞运动的速度等于12m/s
B.当O、P、Q在同一直线时,活塞运动的速度为零
C.当PQ垂直于OP时,活塞运动的速度为10m/s
D.当PQ垂直于OP时,活塞运动的速度为15m/s
(多选)8.(2024秋 越秀区期末)如图所示为水平面上一个边长为1m的正方体空间,某一质量为0.1kg的质点自O点由静止开始运动,除重力外,该质点还同时受到F1、F2两个恒力作用,且F1=F2=1N如图所示,g取10m/s2。则该质点( )
A.加速度大小为
B.将沿OB连线飞出正方体
C.在正方体区域内运动时间为1s
D.在正方体区域内运动时间为
(多选)9.(2024秋 武汉期末)如图所示,轻杆AB的中点固定着小球C,现使A端不脱离墙面,B端在水平面上以v向右匀速运动。当杆与水平面成α角时,下列说法正确的是( )
A.杆上A端的速度大小为
B.小球C的速度大小为
C.杆对小球C的作用力方向一定沿竖直方向
D.杆对小球C的作用力方向一定沿杆方向
三.填空题(共3小题)
10.(2024秋 黄浦区校级期末)一渡船在宽为d的河中航行。现从码头出发,船头垂直于河岸,以速度v匀速驶向对岸,则渡河时间为 ;若越靠近河中央水流速度u越大,则渡船行驶的轨迹示意图为如图的 (选填“甲”或“乙”)。
11.(2024秋 普陀区校级期末)移动射靶的简化情景如图所示,靶沿水平轨道快速横向移动,射手站定不动,用步枪向靶射击。设靶移动的速度大小为v0,子弹出射速度的大小为v,移动靶离射手的最近距离为d。则子弹射中目标的最短时间为 ,此种情况下,射手射击时,枪口离目标的距离为 。
12.(2023秋 嘉定区校级期末)渡过一宽100m的河,船相对静水速度5m/s,水流速度3m/s,则过河最短时间为 s.如果第二天过河的过程中突发暴雨,水流加快,则过河最短时间 (不变、变大、变小)。
四.解答题(共3小题)
13.(2024秋 辽宁期末)2024年11月12日,第十五届中国国际航空航天博览会在珠海开幕,本届航展期间,“飞行汽车”是最火的展台,打“飞的”去远方或许不久就能实现。一辆飞行汽车在表演时在平直的公路上以20m/s的速度行驶,某时刻驾驶员启动飞行模式,汽车保持水平速度不变,沿竖直方向开始匀加速爬升,经过一段时间爬升到100m高处,用x表示水平位移,y表示竖直位移,这一过程的y﹣x图像如图所示。求汽车飞行时:
(1)从启动飞行模式,到离地100m高处需要多长时间;
(2)到达100m高处时竖直速度和瞬时速度的大小。
14.(2024秋 黄浦区校级期末)一质点在光滑水平面上运动,它的x方向和y方向的两个分速度—时间图像分别如图甲和图乙所示。
(1)可判断质点运动性质为做 (选填“匀变速”或“变加速”) (选填“直线”或“曲线”)运动;
(2)4s时速度v与x轴正方向的夹角为 °;
(3)质点在4s内的位移s大小为 m,请在图丙中大致画出质点的运动轨迹图。
15.(2024秋 城关区校级期末)如图所示,一探险者正从某瀑布上游划船渡河,已知河流的宽度d=200m,此时探险者正处于河流正中央A点处,该点与下游瀑布危险区的最短距离为。已知水流速度为v1=4m/s(sin37°=0.6,cos37°=0.8)。从此时开始计时,
(1)若小船在静水中速度为v2=5m/s,则船到岸的最短时间是多少?所到目的地与河流正对岸间的距离是多少?
(2)若小船在静水中速度为v2=5m/s,则小船以最短的距离到岸时所需时间是多少?此时船头方向与河岸上游的夹角是多少?
(3)为了使小船能避开危险区沿直线到达对岸,小船在静水中的速度至少是多少?
期末押题预测 运动的合成与分解
参考答案与试题解析
一.选择题(共5小题)
1.(2024秋 沙坪坝区校级期末)下列不共线的两个分运动,其合运动轨迹一定是曲线的是( )
A.两个匀速直线运动
B.一个匀速直线运动和一个匀变速直线运动
C.两个匀变速直线运动
D.两个初速度不为零的匀变速直线运动
【考点】分析合运动的轨迹问题;合运动与分运动的关系.
【专题】定性思想;推理法;物体做曲线运动条件专题;理解能力.
【答案】B
【分析】当物体所受的合外力和它速度方向不在同一直线上,物体就是在做曲线运动,即速度方向与加速度方向不同时,物体做曲线运动。
【解答】解:A、两个匀速直线运动的合运动是匀速直线运动,故A错误;
CD、两个分运动的合运动的方向与加速度可能在同一直线,故可能做直线运动,故CD错误;
B、合运动方向与加速度方向一定不再同一直线,故合运动轨迹一定是曲线,故B正确。
故选:B。
【点评】考查对物体做曲线运动条件的理解,熟悉其定义。
2.(2024秋 沙坪坝区校级期末)如图所示,一质点在恒力作用下做曲线运动,从M点运动到N点过程中,质点的速度方向恰好改变了90°,且vM:vN=1:1,下列说法正确的是( )
A.质点从M点到N点的过程中做匀速曲线运动
B.质点在M点受力竖直向下,N点受力水平向右
C.质点从M点到N点的过程中速度先减小后增大
D.质点从M点到N点的过程中受力与水平方向成37°
【考点】一个匀速直线和一个变速直线运动的合成;物体运动轨迹、速度、受力(加速度)的相互判断.
【专题】应用题;定量思想;推理法;运动的合成和分解专题;分析综合能力.
【答案】C
【分析】把质点的运动分解为沿MO方向与ON方向的分运动,应用运动学公式分析答题。
【解答】解:A、质点在恒力作用下运动,质点所受合力不变,加速度不变,质点做匀变速曲线运动,故A错误;
BD、质点沿MO方向做匀减速直线运动且末速度为零,在ON方向做初速度为零的匀加速直线运动,由题意可知:vM:vN=1:1,则质点在MO方向与ON方向的加速度大小相等,在这两个方向所受合力大小相等,质点所受恒力方向与ON方向间夹角的正切值tanθ1,则θ=45°,质点所受合力方向不变,故BD错误;
C、质点从M点到N点过程,速度方向与恒力方向的夹角由钝角变为直角再变为锐角,质点先做减速运动后做加速运动,质点的速度先减小再增大,故C正确。
故选:C。
【点评】根据质点的运动过程,应用运动的合成与分解、运动学规律即可解题。
3.(2024秋 碑林区校级期末)如图所示,光滑水平面上固定两个光滑立柱A和B,两根柔软轻绳对称地跨过两立柱,每根绳的一端系在物体上的O点,另一端施加沿绳方向的等大外力,使物体能沿两绳夹角的角平分线运动,物体质量为m。当绳子之间夹角为2α瞬间,绳端速度大小为v,拉力大小为F,此时物体的速度v物和加速度a物表达式正确的是( )
A. B.v物=2vcosα
C. D.
【考点】关联速度问题;力的合成与分解的应用;牛顿第二定律的简单应用.
【专题】定量思想;合成分解法;运动的合成和分解专题;牛顿运动定律综合专题;推理论证能力.
【答案】D
【分析】把物体的速度分解为沿绳方向和垂直于绳的方向,然后根据矢量法则计算物体的速度;根据牛顿第二定律计算物体的加速度。
【解答】解:AB、把物体的速度分解为沿绳方向和垂直于绳的方向,对左边的绳子来说,画出物体的速度分解图像,如图所示
则v物,故AB错误;
CD、根据牛顿第二定律有2Fcosα=ma物,解得a物,故C错误,D正确。
故选:D。
【点评】知道把物体的速度分解为沿绳方向和垂直于绳的方向是解题的基础。
4.(2024秋 鼓楼区校级期末)某小组通过实验得到了物体在恒定合外力作用下的一条运动轨迹OP曲线,如图所示。以下对该运动给出的几种推理正确的是( )
A.该物体的运动轨迹一定为抛物线
B.该运动可分解为沿x轴方向匀速直线运动和沿y轴方向匀速直线运动
C.该运动一定可分解为沿x轴方向匀加速直线运动和沿y轴方向匀加速直线运动
D.若该物体沿x轴方向为匀速直线运动,则物体所受合力不一定平行于y轴
【考点】合运动与分运动的关系;物体做曲线运动的条件;物体运动轨迹、速度、受力(加速度)的相互判断.
【专题】定性思想;推理法;物体做曲线运动条件专题;理解能力.
【答案】A
【分析】当物体所受合外力的方向与它的速度方向不在同一直线上时,物体就会做曲线运动。
【解答】解:A.恒力表示大小和方向都不变的力,物体加速度方向恒定,但与初速度方向不同,它的运动轨迹就是抛物线.,故A正确;
B.若两个运动都是匀速直线运动,则物体受到的合力为零,不可能做曲线运动,故B错误;
C.若两个方向都做匀加速直线运动,则合力指向第一象限,则不可能像x轴方向弯曲,故C错误;
D.合力指向轨迹的内侧,所以y轴方向为匀速直线运动,则物体所受合力一定指向x轴正方向,故D错误。
故选:A。
【点评】考查对物体做曲线运动条件的理解,熟悉其定义。
5.(2024秋 鼓楼区校级期末)物块B套在倾斜杆上,并用轻绳与物块A相连,今对B施加一个力F(未画出)使物块B沿杆由点M匀速下滑到N点,运动中连接A、B的轻绳始终保持绷紧状态,在下滑过程中,下列说法正确的是( )
A.物块A的速度先变大后变小
B.物块A的速度先变小后变大
C.物块A先处于超重状态,后处于失重状态
D.物块A先处于失重状态,后处于超重状态
【考点】关联速度问题;牛顿第二定律求解多过程问题;超重与失重的概念、特点和判断.
【专题】定量思想;合成分解法;运动的合成和分解专题;推理论证能力.
【答案】B
【分析】把B物体的速度分解为沿绳方向和垂直绳的方向,根据平行四边形定则分析即可;根据加速度方向分析。
【解答】解:把B物体的速度分解为沿绳方向和垂直绳的方向,如图所示
AB、根据平行四边形形定则,沿绳子方向的速度为vA=vBcosθ,θ指绳与杆之间的夹角,所以cosθ先减小后增大,故物块A的速度先变小后变大,故A错误,B正确。
CD、物体A先向下做减速运动,后向上做加速运动,加速度的方向始终向上,所以A始终处于超重状态。故CD错误。
故选:B。
【点评】解决本题的关键是要知道A沿绳子方向上的分速度等于B的速度,以及知道超重状态时物体的加速度的方向向上,失重状态时加道向下即可。
二.多选题(共4小题)
(多选)6.(2024秋 邯郸期末)光滑水平面上建立直角坐标系,质量为m的小球(可视为质点),从y轴上的B点(0,L)以初速度水平向右进入第一象限,经一段时间过x轴上的C点(L,0)时速度大小为。此过程始终受一个平行于xOy平面但方向大小未知的恒力。则( )
A.小球在沿x轴方向上做匀速直线运动
B.小球从B到C的时间为
C.小球所受恒力大小为
D.小球过C点时速度方向与x轴正向夹角为60°
【考点】一个匀速直线和一个变速直线运动的合成;牛顿第二定律的简单应用.
【专题】定量思想;推理法;运动的合成和分解专题;推理论证能力.
【答案】BC
【分析】将恒力沿水平方向以及竖直方向分解,在各个方向上分别利用牛顿运动定律以及运动学公式分析。
【解答】解:ABD.设第一象限恒力的水平分量为Fx,竖直分量为Fy,则
Fx=max
Fy=may
设小球在C点的水平分速度为vx,竖直分速度为vy,速度方向与x轴正向夹角为θ,则
且
解得
,,,θ=53°
故AD错误,B正确;
C.x方向有
可得
Fx=max=4mgy方向有
解得
Fy=may=8mg
则可得
故C正确。
故选:BC。
【点评】运动分解时,各个分运动彼此相互独立,具有等时性。
(多选)7.(2024秋 重庆期末)曲柄连杆结构是发动机实现工作循环、完成能量转化的主要运动零件。如图所示,连杆下端连接活塞Q,上端连接曲轴P。在工作过程中,活塞Q在汽缸内上下做直线运动,带动曲轴绕圆心O旋转,若P做线速度大小为v0=12m/s的匀速圆周运动,已知OP=6m,PQ=8m,则下列说法正确的是( )
A.当OP与OQ垂直时,活塞运动的速度等于12m/s
B.当O、P、Q在同一直线时,活塞运动的速度为零
C.当PQ垂直于OP时,活塞运动的速度为10m/s
D.当PQ垂直于OP时,活塞运动的速度为15m/s
【考点】关联速度问题.
【专题】定量思想;合成分解法;运动的合成和分解专题;推理论证能力.
【答案】ABD
【分析】Q点做直线运动,而P点做匀速圆周运动,将P在两个特殊点的速度分解即可作出判断。
【解答】解:对P和Q的运动分解,如图所示
由关联速度可知vPcosα=vQcosβ,则
A、当OP与OQ垂直时,α=β,P点速度的大小为v0,此时杆PQ整体运动的方向是相同的,方向沿OQ的平行的方向,所以活塞运动的速度等于P点的速度,都是v0=12m/s,故A正确;
B、当O、P、Q在同一直线时,P点的速度方向与OQ方向垂直,沿OQ方向的分速度为0,Q的瞬时速度为0,所以活塞运动的速度等于0,故B正确;
CD、当PQ垂直于OP时,即杆与圆相切,,根据几何关系可得,解得vQ=15m/s,故C错误,D正确。
故选:ABD。
【点评】曲柄连杆结构是发动机的联动速度传送较为复杂,但该题中的两个特殊点的速度关系是比较明显的,要正确理解它们之间的关系。
(多选)8.(2024秋 越秀区期末)如图所示为水平面上一个边长为1m的正方体空间,某一质量为0.1kg的质点自O点由静止开始运动,除重力外,该质点还同时受到F1、F2两个恒力作用,且F1=F2=1N如图所示,g取10m/s2。则该质点( )
A.加速度大小为
B.将沿OB连线飞出正方体
C.在正方体区域内运动时间为1s
D.在正方体区域内运动时间为
【考点】两个变速直线运动的合成.
【专题】定量思想;合成分解法;运动的合成和分解专题;推理论证能力.
【答案】BD
【分析】根据力的合成法则得到质点所受合力大小,然后根据牛顿第二定律得到加速度大小,根据合力方向分析质点的运动方向;根据运动学公式计算质点在正方体区域的运动时间。
【解答】解:AB、根据力的合成法则可知,质点所受合力大小为FN,方向与竖直方向的正切值为,即方向沿OB连线,根据牛顿第二定律可得质点的加速度大小为a,因为质点是从静止出发的,所以质点的运动方向沿OB方向,故A错误,B正确;
CD、因为F1=F2=1N,都等于重力mg,质点沿F1、F2方向的加速度大小都等于重力加速度,则根据l可得质点在正方体区域内的运动时间为:t,故C错误,D正确。
故选:BD。
【点评】掌握力的合成法则是解题的关键,知道把质点的运动分解为力的方向,根据运动学公式计算时间。
(多选)9.(2024秋 武汉期末)如图所示,轻杆AB的中点固定着小球C,现使A端不脱离墙面,B端在水平面上以v向右匀速运动。当杆与水平面成α角时,下列说法正确的是( )
A.杆上A端的速度大小为
B.小球C的速度大小为
C.杆对小球C的作用力方向一定沿竖直方向
D.杆对小球C的作用力方向一定沿杆方向
【考点】关联速度问题.
【专题】定量思想;合成分解法;运动的合成和分解专题;推理论证能力.
【答案】AC
【分析】分解A、B两点的速度,根据它们沿杆方向的速度相等分析;C既有水平方向的速度,也有竖直方向的速度,根据速度矢量合成法则计算;根据C球在水平方向做匀速直线运动,竖直方向做变速运动分析小球C的受力。
【解答】解:A、分解A、B两点的速度,如图所示
则vcosα=vAsinα,解得,故A正确;
B、以墙角为坐标原点,设C点横、纵坐标分别为x、y,杆长为L,则A点纵坐标为2y,B点横坐标为2x,则有(2x)2+(2y)2=L2,可得C点的轨迹方程为,即轨迹为圆,其速率满足,代入数据得 ,故B错误;
CD、C点的水平分速度为B速度的一半,所以C在水平方向上匀速运动,水平方向合力为0,竖直方向变速运动,所以杆对小球C的作用力方向一定沿竖直方向,故C正确,D错误。
故选:AC。
【点评】A、B两端点沿杆方向的分速度相等,C点的水平分速度为B速度的一半,竖直分速度为A的一半,这两点是本题的解题关键。
三.填空题(共3小题)
10.(2024秋 黄浦区校级期末)一渡船在宽为d的河中航行。现从码头出发,船头垂直于河岸,以速度v匀速驶向对岸,则渡河时间为 ;若越靠近河中央水流速度u越大,则渡船行驶的轨迹示意图为如图的 甲 (选填“甲”或“乙”)。
【考点】小船过河问题.
【专题】定量思想;推理法;运动的合成和分解专题;理解能力.
【答案】;甲。
【分析】根据宽度和速度求解时间;根据速度的变化情况分析。
【解答】解:渡船在垂直河岸的方向以速度v匀速向对岸行驶,设渡河时间为t,则有;设合速度方向与河岸方向夹角为θ,则有,若越靠近河中央水的流速越大,即水速u先增大后减小,则沿着河岸方向先加速后减速,而垂直河岸方向为匀速直线运动,则tanθ先减小后增大,即θ先减小和增大,曲线运动速度的方向沿切线方向,则轨迹如图甲。
故答案为:;甲。
【点评】考查对合运动与分运动的关系,属于基础知识。
11.(2024秋 普陀区校级期末)移动射靶的简化情景如图所示,靶沿水平轨道快速横向移动,射手站定不动,用步枪向靶射击。设靶移动的速度大小为v0,子弹出射速度的大小为v,移动靶离射手的最近距离为d。则子弹射中目标的最短时间为 ,此种情况下,射手射击时,枪口离目标的距离为 。
【考点】小船过河问题.
【专题】定量思想;推理法;运动的合成和分解专题;推理论证能力.
【答案】;。
【分析】当子弹垂直轨道运动时,射中目标的位移最小,时间最短。根据最短时间计算移动靶的位移,运用合成法求解距离。
【解答】解:子弹垂直轨道运动时,射中目标的时间最短,为,此种情况下,射手射击时,枪口离目标的距离为。
故答案为:;。
【点评】考查对运动的合成与分解的理解,熟悉和运动与分运动的关联。
12.(2023秋 嘉定区校级期末)渡过一宽100m的河,船相对静水速度5m/s,水流速度3m/s,则过河最短时间为 20 s.如果第二天过河的过程中突发暴雨,水流加快,则过河最短时间 不变 (不变、变大、变小)。
【考点】合运动与分运动的关系.
【专题】定量思想;推理法;运动的合成和分解专题;推理论证能力.
【答案】20;不变。
【分析】将船的运动分解成垂直、平行河岸两个方向,船头垂直于河岸航行时所用时间最短。
【解答】解:船头垂直于河岸航行时所用时间最短,此种情况渡河时间为,过河的时间与河水的流速无关,水流加快时,过河时间不变。
故答案为:20;不变。
【点评】考查对运动的合成与分解的理解,将船的运动分解成垂直、平行河岸两个方向,分析垂直方向的运动即可。
四.解答题(共3小题)
13.(2024秋 辽宁期末)2024年11月12日,第十五届中国国际航空航天博览会在珠海开幕,本届航展期间,“飞行汽车”是最火的展台,打“飞的”去远方或许不久就能实现。一辆飞行汽车在表演时在平直的公路上以20m/s的速度行驶,某时刻驾驶员启动飞行模式,汽车保持水平速度不变,沿竖直方向开始匀加速爬升,经过一段时间爬升到100m高处,用x表示水平位移,y表示竖直位移,这一过程的y﹣x图像如图所示。求汽车飞行时:
(1)从启动飞行模式,到离地100m高处需要多长时间;
(2)到达100m高处时竖直速度和瞬时速度的大小。
【考点】一个匀速直线和一个变速直线运动的合成;匀变速直线运动规律的综合应用.
【专题】定量思想;方程法;直线运动规律专题;理解能力.
【答案】(1)从启动飞行模式,到离地100m高处需要10s;
(2)到达100m高处时竖直速度为20m/s,瞬时速度的大小为。
【分析】(1)根据水平方向速度与位移求解时间;
(2)根据匀变速直线运动推论求解竖直速度,根据分速度求解合速度。
【解答】解:(1)飞行汽车的水平速度不变,当爬升到100m高处时有x=v0t,解得t10s;
(2)竖直方向做匀加速直线运动,有,解得;
合速度为。
答:(1)从启动飞行模式,到离地100m高处需要10s;
(2)到达100m高处时竖直速度为20m/s,瞬时速度的大小为。
【点评】考查对匀变速直线运动规律的理解和分速度与合速度的关系,熟悉运动学公式的运用。
14.(2024秋 黄浦区校级期末)一质点在光滑水平面上运动,它的x方向和y方向的两个分速度—时间图像分别如图甲和图乙所示。
(1)可判断质点运动性质为做 匀变速 (选填“匀变速”或“变加速”) 曲线 (选填“直线”或“曲线”)运动;
(2)4s时速度v与x轴正方向的夹角为 37 °;
(3)质点在4s内的位移s大小为 16 m,请在图丙中大致画出质点的运动轨迹图。
【考点】运动的合成与分解的图像类问题;一个匀速直线和一个变速直线运动的合成.
【专题】定量思想;推理法;运动学中的图象专题;理解能力.
【答案】(1)匀变速,曲线;
(2)37;
(3)16,。
【分析】v﹣t图像反映了做直线运动的物体的速度随时间变化的规律,斜率表示加速度的大小及方向,图线与时间轴所包围的“面积”表示位移。
【解答】解:(1)由图可知,该质点沿x方向做匀速直线运动,沿y方向做匀变速直线运动,0~2s内y方向速度匀速减小,2~4s内y方向速度匀速增大,可知合力的方向沿y方向,与和速度方向不一致,故质点做曲线运动;
(2)4s时速度vx=4m/s,vy=﹣3m/s,设与x轴正方向的夹角为θ,根据几何关系得,解得θ=37°;
(3)v﹣t图像与时间轴所包围的“面积”表示位移,可得4s内x轴方向的位移为xx=4×4m=16m,y轴方向的位移为,y轴方向的最大位移为,质点在4s内的位移s大小为16m,质点的运动轨迹如图
。
故答案为:(1)匀变速,曲线;
(2)37;
(3)16,。
【点评】考查对v﹣t图像的理解,清楚图线的含义。
15.(2024秋 城关区校级期末)如图所示,一探险者正从某瀑布上游划船渡河,已知河流的宽度d=200m,此时探险者正处于河流正中央A点处,该点与下游瀑布危险区的最短距离为。已知水流速度为v1=4m/s(sin37°=0.6,cos37°=0.8)。从此时开始计时,
(1)若小船在静水中速度为v2=5m/s,则船到岸的最短时间是多少?所到目的地与河流正对岸间的距离是多少?
(2)若小船在静水中速度为v2=5m/s,则小船以最短的距离到岸时所需时间是多少?此时船头方向与河岸上游的夹角是多少?
(3)为了使小船能避开危险区沿直线到达对岸,小船在静水中的速度至少是多少?
【考点】小船过河问题;合运动与分运动的关系.
【专题】计算题;定量思想;推理法;运动的合成和分解专题;推理论证能力.
【答案】(1)船到岸的最短时间是20s,所到目的地与河流正对岸间的距离是80m。
(2)小船以最短的距离到岸时所需时间是,此时船头方向与河岸上游的夹角是37°;
(3)为了使小船能避开危险区沿直线到达对岸,小船在静水中的速度至少是2m/s。
【分析】(1)根据船头方向垂直河岸时,则渡河时间最短,结合运动学公式,即可求解;
(2)当船的合速度垂直河岸时,渡河的位移最小,结合三角知识,及运动学公式,即可求解;
(3)当小船在静水中的速度与合速度垂直时,借助于平行四边形定则,即可求出小船在静水中最小速度。
【解答】解:(1)当船头方向垂直河岸时,则渡河时间最短,则最短时间为t,解得t20s;
所到目的地与河流正对岸间的距离x=v1t,解得x=4×20m=80m;
(2)设船头与河岸的夹角为θ,如图
由图知,解得θ=37°
船的合速度,
渡河时间;
(3)小船避开危险区沿直线到达对岸,合速度与水流速度的夹角为α,即有,则α=30°
小船在河水中运动时,当小船在静水中的速度与合速度垂直时,小船在静水中的速度最小为vmin=v1sinα=4×sin30°m/s=2m/s。
答:(1)船到岸的最短时间是20s,所到目的地与河流正对岸间的距离是80m。
(2)小船以最短的距离到岸时所需时间是,此时船头方向与河岸上游的夹角是37°;
(3)为了使小船能避开危险区沿直线到达对岸,小船在静水中的速度至少是2m/s。
【点评】本题属于:一个速度要分解,已知一个分速度的大小与方向,还已知另一个分速度的大小且最小,则求这个分速度的方向与大小值;这种题型运用平行四边形定则,由几何关系来确定最小值;同时掌握渡河时间最短,与渡河位移最小的求解方法。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 抛体运动
- 1 认识曲线运动
- 2 运动的合成与分解
- 3 探究平抛运动的特点
- 4 研究平抛运动的规律
- 5 斜抛运动(选学)
- 第二章 匀速圆周运动
- 1 圆周运动
- 2 匀速圆周运动的向心力和向心加速度
- 3 圆周运动的实例分析
- 4 圆周运动与人类文明(选学)
- 第三章 万有引力定律
- 1 天体运动
- 2 万有引力定律
- 3 预言未知星体 计算天体质量
- 4 人造卫星宇宙
- 5 太空探索(选学)
- 第四章 机械能及其守恒定律
- 1 功
- 2 功率
- 3 动能 动能定理
- 4 势能
- 5 机械能守恒定律
- 6 实验:验证机械能守恒定律
- 第五章 经典力学的局限性与相对论初步
- 1 经典力学的成就与局限性
- 2 相对论时空观简介
- 3 宇宙的起源和演化
