19.2.2 第3课时 用待定系数法求一次函数解析式 课件(共33张PPT)
文档属性
| 名称 | 19.2.2 第3课时 用待定系数法求一次函数解析式 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 884.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-28 05:25:13 | ||
图片预览










文档简介
(共33张PPT)
19.2.2 一次函数
第十九章 一次函数
第3课时 用待定系数法求
一次函数的解析式
学习目标
前面,我们学习了一次函数及其图象和性质,你能写出两个具体的一次函数解析式吗?如何画出它们的图象?
思考:
反过来,已知一个一次函数的图象经过两个具体的点,你能求出它的解析式吗?
两点法——两点确定一条直线
情景导入
解:设这个一次函数的解析式为y=kx+b.
3k+b=5,
-4k+b=-9,
∴这个一次函数的解析式为
解方程组得
b=-1.
把点(3,5)与(-4,-9)分别代入,得:
k=2,
y=2x-1.
例1.已知一次函数的图象过点(3,5)与(-4,-9),求这个一次函数的解析式.
课本例题
像这样,通过先设定函数解析式(确定函数模型),再根据条件确定解析式中的未知系数,从而求出函数解析式的方法称为待定系数法.
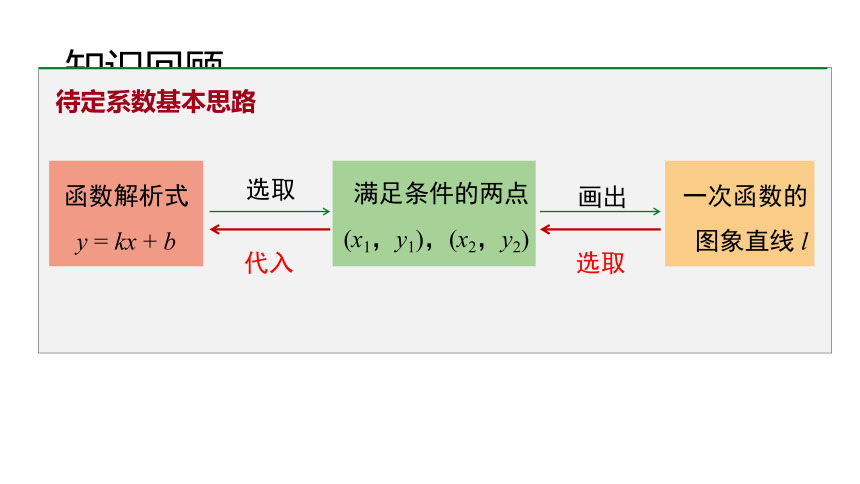
知识回顾
待定系数基本思路
函数解析式
y = kx + b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的
图象直线 l
选取
代入
画出
选取
待定系数的步骤
(1)设:设一次函数的一般形式y = kx + b (k ≠ 0);
(2)列:把图象上的点 (x1,y1),(x2,y2) 代入一次函数的解析式,组成二元一次方程组;
(3)解:解二元一次方程组得 k,b;
(4)写:把 k,b 的值代入一次函数的解析式,写出结果.
做一做
已知一次函数的图象过点(3,5)与(-4,-9),
求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b.
3k+b=5,
-4k+b=-9,
∴这个一次函数的解析式为
解方程组得
b=-1.
把点(3,5)与(-4,-9)分别代入,得:
k=2,
y=2x-1.
(1)设:设一次函数的一般形式 ;
(2)列:把图象上的点 , 代入一次函数的解析式,组成_________方程组;
(3)解:解二元一次方程组得k,b;
(4)还原:把k,b的值代入一次函数的解析式.
求一次函数解析式的步骤:
y=kx+b(k≠0)
二元一次
归纳总结
例3 已知一次函数的图象过点(0,2),且与两坐标轴围成的三角形的面积为2,求此一次函数的解析式.
分析:一次函数y=kx+b与y轴的交点是(0,b),与x轴的交点是( ,0).由题意可列出关于k,b的方程.
y
x
O
2
注意:此题有两种情况.
典例精析3 几何面积和待定系数法求一次函数的解析式
合作探究
解:设一次函数的解析式为y=kx+b(k≠0).
∵一次函数y=kx+b的图象过点(0,2),
∴b=2.
∵一次函数的图象与x轴的交点是( ,0),则
解得k=1或-1.
故此一次函数的解析式为y=x+2或y=-x+2.
正比例函数y=k1x与一次函数y=k2x+b的图象如图所示,它们的交点A的坐标为(3,4),并且OB=5.
(1)你能求出这两个函数的解析式吗?
(2)△AOB的面积是多少呢?
分析:由OB=5可知点B的坐标为(0,-5).y=k1x的图象过点A(3,4),y=k2x+b的图象过点
A(3,4),B(0,-5),代入解方程(组)即可.
4
2
-2
-4
4
x
y
O
-4
-2
2
A
(3,4)
B
巩固新知
解:(1)由题意可知,B点的坐标是(0,-5).
∵一次函数y=k2x+b的图象过点(0,-5),(3,4),
∴
∵正比例函数y=k1x的图象过点(3,4),
∴ 因此
(2)S△AOB=5×3÷2=7.5.
因此y=3x-5.
4
2
-2
-4
4
x
y
O
-4
-2
2
A
(3,4)
B
解得
已知一次函数的图象经过两点(1,4)、( -1,0),求这个一次函数的解析式.
解:设这个一次函数解析式为 y=kx+b(k≠0)
∵一次函数图象经过两点(1,4)、( -1,0 )
k+b=4
-k+b=0
∴
k=2
b=2
解得:
∴ 这个一次函数解析式为 y=2x+2.
巩固新知
一次函数解析式
待定系数法
应用
先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法.
①设;②列;③解;④代.
步骤
①已知一次函数解析式
②题目中未给出一次函数解析式
归纳新知
C
x -1 0 1
y 1 m -5
课堂练习
C
3.与直线y=2x+5平行,且与x轴相交于点M(-2,0)的直线的解析式为( )
A.y=2x+4 B.y=2x-2
C.y=-2x-4 D.y=-2x-2
A
4.如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是( )
A.y=2x+3 B.y=x-3
C.y=2x-3 D.y=-x+3
D
1.一次函数 y = kx + b (k ≠ 0) 的图象如图,则下列结论正确的是 ( )
A.k = 2 B.k = 3
C.b = 2 D.b = 3
D
y
x
O
2
3
基础练习
课堂练习
2.小明将父母给的零用钱按每月相等的数额存在储蓄盒内,准备捐给希望工程,盒内钱数 y (元)与存钱月数 x (月) 之间的关系如图所示,根据下图回答下列问题:
(1)求出 y 关于 x 的函数解析式.
(2)根据关系式计算,小明
经过几个月才能存够 200 元?
40
80
120
y/元
x/月
1
2
3
4
5
o
解:(1) 设函数解析式为 y = kx+b,
由图可知图象过(0,40),(4,120),
∴ 这个函数的解析式为 y = 20x + 40.
(2) 当 y = 200 时,20x + 40 = 200, 解得 x = 8.
∴小明经过 8 个月才能存够 200 元.
40
80
120
y/元
x/月
1
2
3
4
5
o
解:设直线 l 为 y = kx + b,
∵ l 与直线 y = -2x 平行,∴ k = -2.
又∵ 直线过点(0,2),
∴ 2 = -2×0 + b.
∴ b = 2,
∴ 直线 l 的解析式为 y = - 2x + 2.
3. 已知直线 l 与直线 y = -2x 平行,且与 y 轴交于点(0,2),求直线 l 的解析式.
4. 如图,一次函数 y = kx + b 的图象交 x 轴于点
A (2, 0),交 y 轴于点 B (0,4),P 是线段 AB 上的一点(不与端点重合),过点 P 作 PC⊥x 轴于点 C.
(1) 求直线 AB 的函数解析式.
(2) 设点 P 的横坐标为 m,若 PC<3,
求 m 的取值范围.
能力提升
解:(1) 将 A (2,0),B (0,4)代入 y = kx + b,得
则直线 AB 的解析式为:y = - 2x + 4.
(2) 当 PC = 3 时,- 2m + 4 = 3,
解得 m =
故 m 的取值范围为:
解得
2
19.2.2 一次函数
第十九章 一次函数
第3课时 用待定系数法求
一次函数的解析式
学习目标
前面,我们学习了一次函数及其图象和性质,你能写出两个具体的一次函数解析式吗?如何画出它们的图象?
思考:
反过来,已知一个一次函数的图象经过两个具体的点,你能求出它的解析式吗?
两点法——两点确定一条直线
情景导入
解:设这个一次函数的解析式为y=kx+b.
3k+b=5,
-4k+b=-9,
∴这个一次函数的解析式为
解方程组得
b=-1.
把点(3,5)与(-4,-9)分别代入,得:
k=2,
y=2x-1.
例1.已知一次函数的图象过点(3,5)与(-4,-9),求这个一次函数的解析式.
课本例题
像这样,通过先设定函数解析式(确定函数模型),再根据条件确定解析式中的未知系数,从而求出函数解析式的方法称为待定系数法.
知识回顾
待定系数基本思路
函数解析式
y = kx + b
满足条件的两点
(x1,y1),(x2,y2)
一次函数的
图象直线 l
选取
代入
画出
选取
待定系数的步骤
(1)设:设一次函数的一般形式y = kx + b (k ≠ 0);
(2)列:把图象上的点 (x1,y1),(x2,y2) 代入一次函数的解析式,组成二元一次方程组;
(3)解:解二元一次方程组得 k,b;
(4)写:把 k,b 的值代入一次函数的解析式,写出结果.
做一做
已知一次函数的图象过点(3,5)与(-4,-9),
求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b.
3k+b=5,
-4k+b=-9,
∴这个一次函数的解析式为
解方程组得
b=-1.
把点(3,5)与(-4,-9)分别代入,得:
k=2,
y=2x-1.
(1)设:设一次函数的一般形式 ;
(2)列:把图象上的点 , 代入一次函数的解析式,组成_________方程组;
(3)解:解二元一次方程组得k,b;
(4)还原:把k,b的值代入一次函数的解析式.
求一次函数解析式的步骤:
y=kx+b(k≠0)
二元一次
归纳总结
例3 已知一次函数的图象过点(0,2),且与两坐标轴围成的三角形的面积为2,求此一次函数的解析式.
分析:一次函数y=kx+b与y轴的交点是(0,b),与x轴的交点是( ,0).由题意可列出关于k,b的方程.
y
x
O
2
注意:此题有两种情况.
典例精析3 几何面积和待定系数法求一次函数的解析式
合作探究
解:设一次函数的解析式为y=kx+b(k≠0).
∵一次函数y=kx+b的图象过点(0,2),
∴b=2.
∵一次函数的图象与x轴的交点是( ,0),则
解得k=1或-1.
故此一次函数的解析式为y=x+2或y=-x+2.
正比例函数y=k1x与一次函数y=k2x+b的图象如图所示,它们的交点A的坐标为(3,4),并且OB=5.
(1)你能求出这两个函数的解析式吗?
(2)△AOB的面积是多少呢?
分析:由OB=5可知点B的坐标为(0,-5).y=k1x的图象过点A(3,4),y=k2x+b的图象过点
A(3,4),B(0,-5),代入解方程(组)即可.
4
2
-2
-4
4
x
y
O
-4
-2
2
A
(3,4)
B
巩固新知
解:(1)由题意可知,B点的坐标是(0,-5).
∵一次函数y=k2x+b的图象过点(0,-5),(3,4),
∴
∵正比例函数y=k1x的图象过点(3,4),
∴ 因此
(2)S△AOB=5×3÷2=7.5.
因此y=3x-5.
4
2
-2
-4
4
x
y
O
-4
-2
2
A
(3,4)
B
解得
已知一次函数的图象经过两点(1,4)、( -1,0),求这个一次函数的解析式.
解:设这个一次函数解析式为 y=kx+b(k≠0)
∵一次函数图象经过两点(1,4)、( -1,0 )
k+b=4
-k+b=0
∴
k=2
b=2
解得:
∴ 这个一次函数解析式为 y=2x+2.
巩固新知
一次函数解析式
待定系数法
应用
先设出函数解析式,再根据条件确定解析式中未知的系数,从而得出函数解析式的方法.
①设;②列;③解;④代.
步骤
①已知一次函数解析式
②题目中未给出一次函数解析式
归纳新知
C
x -1 0 1
y 1 m -5
课堂练习
C
3.与直线y=2x+5平行,且与x轴相交于点M(-2,0)的直线的解析式为( )
A.y=2x+4 B.y=2x-2
C.y=-2x-4 D.y=-2x-2
A
4.如图,过A点的一次函数的图象与正比例函数y=2x的图象相交于点B,则这个一次函数的解析式是( )
A.y=2x+3 B.y=x-3
C.y=2x-3 D.y=-x+3
D
1.一次函数 y = kx + b (k ≠ 0) 的图象如图,则下列结论正确的是 ( )
A.k = 2 B.k = 3
C.b = 2 D.b = 3
D
y
x
O
2
3
基础练习
课堂练习
2.小明将父母给的零用钱按每月相等的数额存在储蓄盒内,准备捐给希望工程,盒内钱数 y (元)与存钱月数 x (月) 之间的关系如图所示,根据下图回答下列问题:
(1)求出 y 关于 x 的函数解析式.
(2)根据关系式计算,小明
经过几个月才能存够 200 元?
40
80
120
y/元
x/月
1
2
3
4
5
o
解:(1) 设函数解析式为 y = kx+b,
由图可知图象过(0,40),(4,120),
∴ 这个函数的解析式为 y = 20x + 40.
(2) 当 y = 200 时,20x + 40 = 200, 解得 x = 8.
∴小明经过 8 个月才能存够 200 元.
40
80
120
y/元
x/月
1
2
3
4
5
o
解:设直线 l 为 y = kx + b,
∵ l 与直线 y = -2x 平行,∴ k = -2.
又∵ 直线过点(0,2),
∴ 2 = -2×0 + b.
∴ b = 2,
∴ 直线 l 的解析式为 y = - 2x + 2.
3. 已知直线 l 与直线 y = -2x 平行,且与 y 轴交于点(0,2),求直线 l 的解析式.
4. 如图,一次函数 y = kx + b 的图象交 x 轴于点
A (2, 0),交 y 轴于点 B (0,4),P 是线段 AB 上的一点(不与端点重合),过点 P 作 PC⊥x 轴于点 C.
(1) 求直线 AB 的函数解析式.
(2) 设点 P 的横坐标为 m,若 PC<3,
求 m 的取值范围.
能力提升
解:(1) 将 A (2,0),B (0,4)代入 y = kx + b,得
则直线 AB 的解析式为:y = - 2x + 4.
(2) 当 PC = 3 时,- 2m + 4 = 3,
解得 m =
故 m 的取值范围为:
解得
2
