第七单元图形的运动(二)(知识梳理+拔高训练)二2024-2025学年四年级数学下学期培优检测卷(人教版含答案)
文档属性
| 名称 | 第七单元图形的运动(二)(知识梳理+拔高训练)二2024-2025学年四年级数学下学期培优检测卷(人教版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-05-27 09:35:22 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第七单元图形的运动(二)(知识梳理+拔高训练)二
知识梳理
知识点01:轴对称
把一个图形沿着某一条直线对折,如果直线两旁的部分能够完全重合,我们就说这个图形是轴对称图形,这条直线叫做这个图形的对称轴。
轴对称的性质:对应点到对称轴的距离都相等。
对称轴是一条直线,所以在画对称轴时,要画到图形外面,且要用虚线。
正方形的对角线所在的直线是它的对称轴。轴对称图形可以有一条或几条对称轴。
画对称轴时,先找到与相反方向距离对称轴相同的对应点,最后连线。
长方形、正方形、等腰梯形、等腰三角形、等边三角形、线段、菱形都是轴对称图形。
平行四边形不是轴对称图形,没有对称轴。(长方形和正方形除外)
梯形不一定是轴对称图形。只有等腰梯形是轴对称图形。
古今中外,许多著名的建筑就是对称的。比如:中国的赵州桥,印度泰姬陵,英国塔桥,法国埃菲尔铁塔。
知识点02:平移
平移先找图形点,平移完点连起来,注意数点数要数十字。
平移不改变图形的大小、形状,只改变图形的位置。
利用平移,可以求出不规则图形的面积。
拔高训练
一、填空题
1.下图每格边长是1cm。这幅小鱼图的面积是( )cm2。
2.哪一幅图是由左边的图形平移得到,在后面的括号里画“√”。
3.如图,把平行四边形ABCD的左边这一小部分剪下来,向( )平移( )格,就可以拼成一个长方形。这个长方形面积是( )cm2。(1格代表1cm2)
4.在常见的平面图形中,等边三角形有( )条对称轴,( )有无数条对称轴。
5.“徽州三雕”是徽派文化中最具代表性的艺术,名列第一批国家级非物质文化遗产名录。下图是徽州花窗的平面图,仔细观察,图形A通过( )可以得到图形B,图形B通过( )能得到图形C。
6.如图,将( )号小正方形向( )平移( )格可以得到大写英文字母“T”。
7.下面图形中有2条对称轴的是( ),有4条对称轴的是( ),有无数条对称轴的是( )(填序号)。
①. ②. ③.
8.数学的对称美无处不在,“”是一个汉字的左半部分,那么完整的汉字可能是( )。
二、选择题
9.下列图形中,对称轴条数最多的是( )。
A. B. C.
10.通过平移,能和下面的( )重合。
A. B. C.
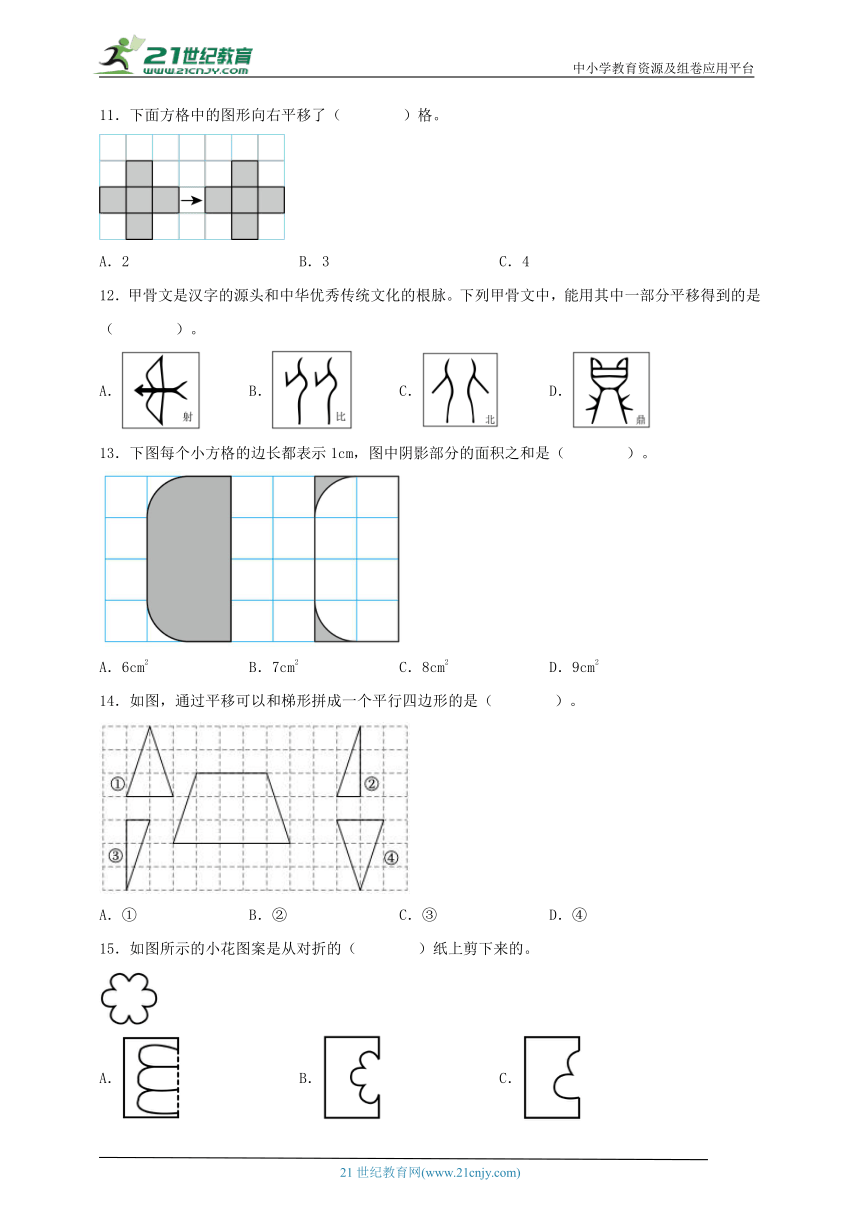
11.下面方格中的图形向右平移了( )格。
A.2 B.3 C.4
12.甲骨文是汉字的源头和中华优秀传统文化的根脉。下列甲骨文中,能用其中一部分平移得到的是( )。
A. B. C. D.
13.下图每个小方格的边长都表示1cm,图中阴影部分的面积之和是( )。
A.6cm2 B.7cm2 C.8cm2 D.9cm2
14.如图,通过平移可以和梯形拼成一个平行四边形的是( )。
A.① B.② C.③ D.④
15.如图所示的小花图案是从对折的( )纸上剪下来的。
A. B. C.
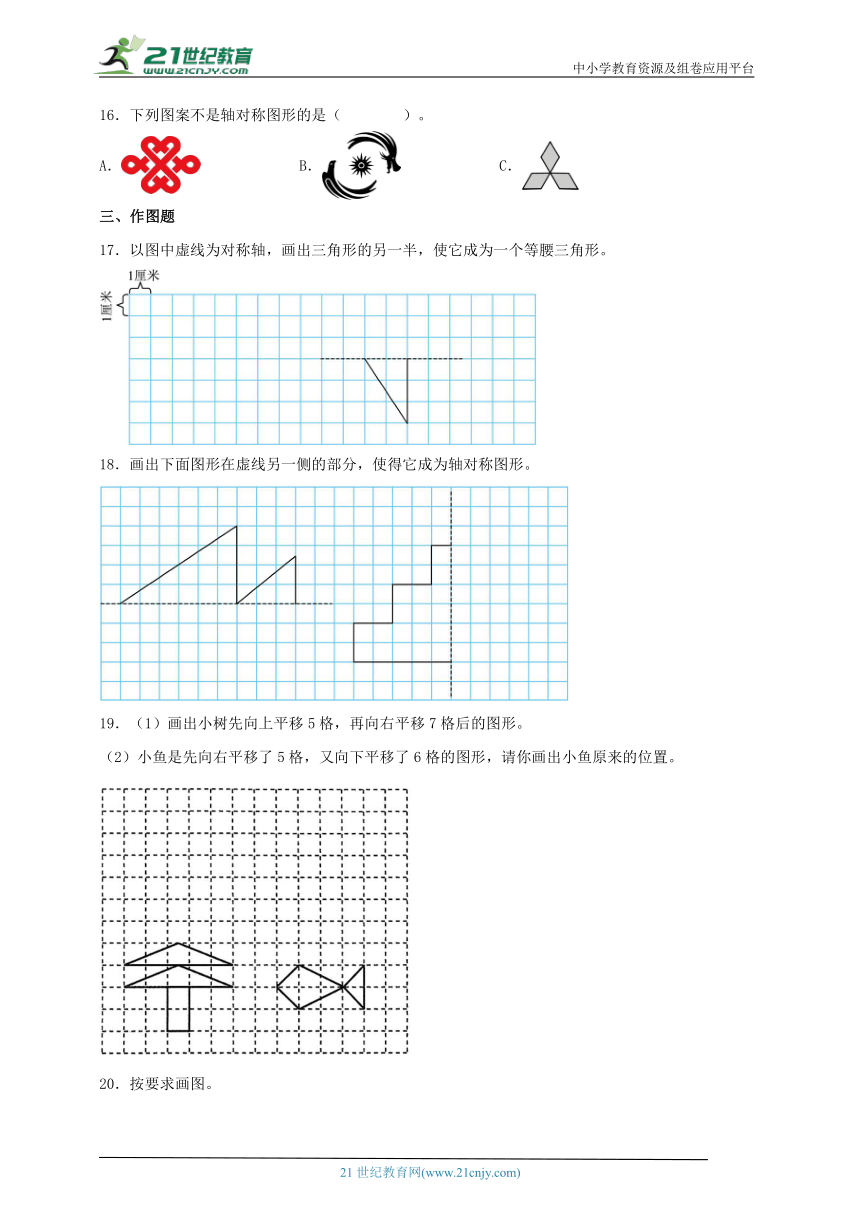
16.下列图案不是轴对称图形的是( )。
A. B. C.
三、作图题
17.以图中虚线为对称轴,画出三角形的另一半,使它成为一个等腰三角形。
18.画出下面图形在虚线另一侧的部分,使得它成为轴对称图形。
19.(1)画出小树先向上平移5格,再向右平移7格后的图形。
(2)小鱼是先向右平移了5格,又向下平移了6格的图形,请你画出小鱼原来的位置。
20.按要求画图。
(1)根据对称轴补全轴对称图形①。
(2)画出将图形②向上平移2格、向左平移5格后得到的图形。
(3)按边分,图形②是( )三角形;按角分,图形②是( )三角形。
四、解答题
21.在一块长30米、宽20米的长方形草地上有两条宽1米的小路,如图,求草坪的面积。
22.学校艺术楼门前要建一个如图所示长12米,宽2米的花坛,如果在花坛边铺一条小路,求小路长多少米?
23.按要求完成下面各题。(每个小方格的边长表示1厘米)
(1)根据对称轴补全上面这个轴对称图形。
(2)这个轴对称图形的周长是( )厘米。
(3)画出这个轴对称图形向左平移4格后的图形。
24.按要求完成下面题目。
(1)先从ABCD四个点中任选3个点画一个三角形。这是一个( )三角形。
(2)然后画出三角形向下平移6格后的图形。
(3)再在平移前的三角形中,以最长边为底,画出底边上的高。
(4)画出轴对称图形的另一半。
25.按要求完成下面各题。(下面每个小方格的每边的长表示1厘米)“晴川历历汉阳树,芳革萋婆鹦鹉洲”位于汉阳江滩的晴川阁因唐代诗人崔顾的诗句而闻名,晴川阁与黄鹤楼、古琴台并称“三楚圣境”,建筑整体体现了轴对称,一起去打卡吧!
(1)以虚线为对称轴,画出轴对称图形的另一半。
(2)画出这个轴对称图形向右平移16格后的图形。
(3)这个轴对称图形的面积是________。
参考答案
1.16
【分析】根据平移把上面半圆向下平移至下面半圆处,再把右边三角形向左平移至左边三角形处,组成一个正方形,根据正方形面积=边长×边长计算,这个正方形边长是4cm。
【详解】由分析可知:图形面积为4×4=16(cm2)
这幅小鱼图的面积是16cm2。
2.见详解
【分析】根据平移的定义:在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动。平移后图形的位置改变,形状,大小,方向不变。
【详解】根据分析:
3. 右 5 10
【分析】把平行四边形ABCD的左边这一小部分剪下来向右平移,找A点平移后对应的D点平移了几格。数出长有5格为5cm,宽有2格为2cm,再根据长方形面积=长×宽计算。
【详解】5×2=10(cm2)
如图,把平行四边形ABCD的左边这一小部分剪下来,向右平移5格,就可以拼成一个长方形。这个长方形面积是10cm2。
4. 3 圆
【分析】根据轴对称图形的定义:如果一个图形沿一条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形,这条直线就是它的对称轴。
【详解】如图:
在常见的平面图形中,等边三角形有3条对称轴,圆有无数条对称轴。
5. 轴对称 平移
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴;在平面内,把一个图形整体沿某条直线方向平行移动一定距离的过程,称为平移;平移前后,物体的大小、形状和方向均不会改变,只是位置发生变化。
【详解】由图可知,图形A和图形B关于中间的直线对称,所以图形A通过轴对称可以得到图形B;图形B和图形C形状、大小和方向都一样,所以图形B通过平移能得到图形C。
仔细观察,图形A通过轴对称可以得到图形B,图形B通过平移能得到图形C。
6. ④ 左 2
【分析】在平面内,把一个图形整体沿某条直线方向平行移动一定距离的过程,称为平移。
根据题意可知,把④号小正方形平移到图中③号和⑤号小正方形之间就可以得到大写英文字母“T”。据此解答。
【详解】根据分析可知, 通过平移④号小正方形可得到大写英文字母“T”,如下图:
则将④号小正方形向左平移2格可以得到大写英文字母“T”。
7. ② ③ ①
【分析】轴对称图形定义为平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形。直线叫做对称轴,并且对称轴用点画线表示,据此判断图形有几条对称轴即可。
【详解】
①如图:,圆形有无数条对称轴;
②如图:,该图形有两条对称轴;
③如图:,该图形有四条对称轴。
图形中有2条对称轴的是②,有4条对称轴的是③,有无数条对称轴的是①。
8.非
【分析】沿一条直线对折后两部分可以完全重合的图形叫做轴对称图形。把图形补全,使它成为一个轴对称图形,需要在对称轴的另一侧找到对应的顶点,依次连接这些点;据此解答。
【详解】根据解析补成完整以后的汉字是,所以完整的汉字可能是非。
9.C
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴。分析每个选项中图形的对称轴数量,选出符合要求的即可。
【详解】A.正方形有4条对称轴;
B.长方形有2条对称轴;
C.五角星有5条对称轴。
5>4>2
所以,五角星的对称轴数量最多。
故答案为:C
10.B
【分析】在平面内,把一个图形整体沿某条直线方向平行移动一定距离的过程,称为平移;平移前后,物体的大小、形状和方向均不会改变,只是位置发生变化。由题意得,平移原来的图形,要使它和其它图形能够重合,那么它们的大小、形状和方向均应该相同。
【详解】A.由图可知,选项中的小鸟与原来图形的方向不一样。不满足题意。
B.由图可知,选项中的小鸟与原来图形的大小、形状和方向均一样。满足题意。
C.由图可知,选项中的小鸟与原来图形的大小不一样。不满足题意。
故答案为:B
11.C
【分析】数平移的距离可以在找出图形中任意找出某个“关键点”,这个“关键点”平移之前的位置和平移之后的位置之间的距离,就是平移的距离。如下图,两个红点之间的距离是4格,也就是图形向右平移了4格。据此解题即可。
【详解】由分析可知:题中方格中的图形向右平移了4格。
故答案为:C
12.B
【分析】平移:在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动。平移后图形的位置改变,形状、大小、方向不变。据此解答即可。
【详解】
A.,不能用其中一部分平移得到;
B.,可以用其中一部分平移得到;
C.,不能用其中一部分平移得到;
D.,不能用其中一部分平移得到。
甲骨文是汉字的源头和中华优秀传统文化的根脉。下列甲骨文中,能用其中一部分平移得到的是。
故答案为:B
13.C
【分析】根据题意,可以将左边阴影部分向右平移4格后和右边阴影部分组成一个长为4cm宽为2cm的长方形,根据长方形面积=长×宽,据此代入数字计算出面积选择即可。
【详解】4×2=8(cm2)
图中阴影部分的面积之和是8cm2。
故答案为:C
14.D
【分析】平移,是指在同一平面内,将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动,简称平移。平移不改变图形的形状和大小。
两组对边分别平行且相等的四边形是平行四边形,只有一组对边平行的四边形是梯形;
根据平移移动各三角形与梯形拼一拼,再根据平行四边形特点判断即可得出结论。
【详解】
A.图①向下平移两格,与梯形组成的图形是,不是平行四边形;
B.图②向下平移两格,再向左平移两格,与梯形组成的图形是,不是平行四边形;
C.图③向上平移两格,再向右平移两格,与梯形组成的图形是,不是平行四边形;
D.图④向上平移两格,再向左平移三格,与梯形组成的图形是,是平行四边形;
所以,通过平移可以和梯形拼成一个平行四边形的是④。
故答案为:D
15.B
【分析】把一个图形沿着某一条直线折叠,如果直线两旁的部分能够互相重合,那么称这个图形是轴对称图形,这条直线就是对称轴,据此解答即可。
【详解】
分析可知,如图所示的小花图案是从对折的纸上剪下来的。
故答案为:B。
16.B
【分析】把一个平面图形沿一条直线对折,折痕两边的图形能够完全重合,这样的图形叫做轴对称图形,折痕所在的直线是轴对称图形的对称轴。据此解答。
【详解】
A.沿图中直线对折,折痕两边的图形能够完全重合,是轴对称图形;
B.无论怎么对折,折痕两边的图形不能完全重合,不是轴对称图形;
C. 沿图中直线对折,折痕两边的图形能够完全重合,是轴对称图形;
故答案为:B
17.见详解
【分析】补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。由题意得,补全三角形的另一半后,三角形的两条斜着的边的长度相等,所以这是一个等腰三角形。满足题意。
【详解】
18.见详解
【分析】补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【详解】
19.(1)(2)见详解
【分析】(1)根据平移的特征,把小树的各顶点分别先向上平移5格,再向右平移7格,依次连接即可得到平移后的图形。
(2)根据题意,先把小鱼向上平移6格,再向左平移5格,就可以得到小鱼原来的位置。
【详解】(1)(2)如图:
20.(1)见详解
(2)见详解
(3)等腰;锐角
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出右图的关键点的对称点,依次连结即可;
(2)根据平移的特征,把三角形的各个顶点分别先向上平移2格、再向左平移5格,再依次连结各顶点的对应点,即可得到图形②平移后的图形;
(3)有两条边相等的三角形是等腰三角形;三个角都是锐角的三角形是锐角三角形;据此解答。
【详解】(1)(2)如图:
(3)按边分,图形②是等腰三角形;按角分,图形②是锐角三角形。
21.551平方米
【分析】将这两条小路平移后可知,草坪的面积等于长(30-1)米,宽(20-1)米的长方形的面积,根据长方形的面积=长×宽,求出草坪的面积。
【详解】(30-1)×(20-1)
=29×19
=551(平方米)
答:草坪的面积是551平方米。
22.28米
【分析】把各不规则部分的横线段和竖线段进行平移,可得到所求周长恰好是长为12米,宽为2米的长方形的周长,用(长+宽)×2,即可求出小路长。
【详解】(12+2)×2
=14×2
=28(米)
答:小路长28米。
【点睛】此题主要考查学生对矩形两组对边对应相等的性质的掌握情况,做这类题时还需注意利用平移的思想。
23.(1)(3)见详解
(2)12
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴虚线的下边画出上半图的关键对称点,依次连接即可。
(2)由图可知,这个图形的一周有12个小方格的边长,所以它的周长是12厘米。
(3)根据平移的特征,把这个轴对称图形的各顶点分别向左平移4格,依次连接即可得到平移后的图形。
【详解】(1)(3)如图
;
(2)这个轴对称图形的周长是12厘米。
24.(1)图见详解;等腰;
(2)(3)(4)见详解
【分析】(1)先从ABCD四个点中任选3个点画一个三角形(画法不唯一),等腰三角形的两腰相等,从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底,依此画图。
(2)物体平移的方法是点对点平移,然后将所有点依次连接起来,依此画出平移后的图形。
(3)根据三角形高的意义,在三角形中,从一个顶点向它的对边所在的直线画垂线,顶点到垂足之间的线段叫做三角形的高,再根据过直线外一点画已知条直线的垂线的方法,由此作图即可。
(4)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【详解】(1)先从ABCD四个点中任选3个点画一个三角形。如图:
这是一个等腰三角形。
(2)然后画出三角形向下平移6格后的图形。如图:
(3)再在平移前的三角形中,以最长边为底,画出底边上的高。如图:
(4)画出轴对称图形的另一半。如图:
(三角形画法不唯一)
25.(1)(2)见详解
(3)54平方厘米
【分析】(1)补全轴对称图形的方法:找出图形的关键点,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,依此画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
(3)先数出整格数以及不完整的格数,把不完整格按半格计算,再加上整格数,估算出面积。
【详解】(1)(2)如图:
(3)50+8÷2
=50+4
=54(平方厘米)
这个轴对称图形的面积是54平方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第七单元图形的运动(二)(知识梳理+拔高训练)二
知识梳理
知识点01:轴对称
把一个图形沿着某一条直线对折,如果直线两旁的部分能够完全重合,我们就说这个图形是轴对称图形,这条直线叫做这个图形的对称轴。
轴对称的性质:对应点到对称轴的距离都相等。
对称轴是一条直线,所以在画对称轴时,要画到图形外面,且要用虚线。
正方形的对角线所在的直线是它的对称轴。轴对称图形可以有一条或几条对称轴。
画对称轴时,先找到与相反方向距离对称轴相同的对应点,最后连线。
长方形、正方形、等腰梯形、等腰三角形、等边三角形、线段、菱形都是轴对称图形。
平行四边形不是轴对称图形,没有对称轴。(长方形和正方形除外)
梯形不一定是轴对称图形。只有等腰梯形是轴对称图形。
古今中外,许多著名的建筑就是对称的。比如:中国的赵州桥,印度泰姬陵,英国塔桥,法国埃菲尔铁塔。
知识点02:平移
平移先找图形点,平移完点连起来,注意数点数要数十字。
平移不改变图形的大小、形状,只改变图形的位置。
利用平移,可以求出不规则图形的面积。
拔高训练
一、填空题
1.下图每格边长是1cm。这幅小鱼图的面积是( )cm2。
2.哪一幅图是由左边的图形平移得到,在后面的括号里画“√”。
3.如图,把平行四边形ABCD的左边这一小部分剪下来,向( )平移( )格,就可以拼成一个长方形。这个长方形面积是( )cm2。(1格代表1cm2)
4.在常见的平面图形中,等边三角形有( )条对称轴,( )有无数条对称轴。
5.“徽州三雕”是徽派文化中最具代表性的艺术,名列第一批国家级非物质文化遗产名录。下图是徽州花窗的平面图,仔细观察,图形A通过( )可以得到图形B,图形B通过( )能得到图形C。
6.如图,将( )号小正方形向( )平移( )格可以得到大写英文字母“T”。
7.下面图形中有2条对称轴的是( ),有4条对称轴的是( ),有无数条对称轴的是( )(填序号)。
①. ②. ③.
8.数学的对称美无处不在,“”是一个汉字的左半部分,那么完整的汉字可能是( )。
二、选择题
9.下列图形中,对称轴条数最多的是( )。
A. B. C.
10.通过平移,能和下面的( )重合。
A. B. C.
11.下面方格中的图形向右平移了( )格。
A.2 B.3 C.4
12.甲骨文是汉字的源头和中华优秀传统文化的根脉。下列甲骨文中,能用其中一部分平移得到的是( )。
A. B. C. D.
13.下图每个小方格的边长都表示1cm,图中阴影部分的面积之和是( )。
A.6cm2 B.7cm2 C.8cm2 D.9cm2
14.如图,通过平移可以和梯形拼成一个平行四边形的是( )。
A.① B.② C.③ D.④
15.如图所示的小花图案是从对折的( )纸上剪下来的。
A. B. C.
16.下列图案不是轴对称图形的是( )。
A. B. C.
三、作图题
17.以图中虚线为对称轴,画出三角形的另一半,使它成为一个等腰三角形。
18.画出下面图形在虚线另一侧的部分,使得它成为轴对称图形。
19.(1)画出小树先向上平移5格,再向右平移7格后的图形。
(2)小鱼是先向右平移了5格,又向下平移了6格的图形,请你画出小鱼原来的位置。
20.按要求画图。
(1)根据对称轴补全轴对称图形①。
(2)画出将图形②向上平移2格、向左平移5格后得到的图形。
(3)按边分,图形②是( )三角形;按角分,图形②是( )三角形。
四、解答题
21.在一块长30米、宽20米的长方形草地上有两条宽1米的小路,如图,求草坪的面积。
22.学校艺术楼门前要建一个如图所示长12米,宽2米的花坛,如果在花坛边铺一条小路,求小路长多少米?
23.按要求完成下面各题。(每个小方格的边长表示1厘米)
(1)根据对称轴补全上面这个轴对称图形。
(2)这个轴对称图形的周长是( )厘米。
(3)画出这个轴对称图形向左平移4格后的图形。
24.按要求完成下面题目。
(1)先从ABCD四个点中任选3个点画一个三角形。这是一个( )三角形。
(2)然后画出三角形向下平移6格后的图形。
(3)再在平移前的三角形中,以最长边为底,画出底边上的高。
(4)画出轴对称图形的另一半。
25.按要求完成下面各题。(下面每个小方格的每边的长表示1厘米)“晴川历历汉阳树,芳革萋婆鹦鹉洲”位于汉阳江滩的晴川阁因唐代诗人崔顾的诗句而闻名,晴川阁与黄鹤楼、古琴台并称“三楚圣境”,建筑整体体现了轴对称,一起去打卡吧!
(1)以虚线为对称轴,画出轴对称图形的另一半。
(2)画出这个轴对称图形向右平移16格后的图形。
(3)这个轴对称图形的面积是________。
参考答案
1.16
【分析】根据平移把上面半圆向下平移至下面半圆处,再把右边三角形向左平移至左边三角形处,组成一个正方形,根据正方形面积=边长×边长计算,这个正方形边长是4cm。
【详解】由分析可知:图形面积为4×4=16(cm2)
这幅小鱼图的面积是16cm2。
2.见详解
【分析】根据平移的定义:在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动。平移后图形的位置改变,形状,大小,方向不变。
【详解】根据分析:
3. 右 5 10
【分析】把平行四边形ABCD的左边这一小部分剪下来向右平移,找A点平移后对应的D点平移了几格。数出长有5格为5cm,宽有2格为2cm,再根据长方形面积=长×宽计算。
【详解】5×2=10(cm2)
如图,把平行四边形ABCD的左边这一小部分剪下来,向右平移5格,就可以拼成一个长方形。这个长方形面积是10cm2。
4. 3 圆
【分析】根据轴对称图形的定义:如果一个图形沿一条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形,这条直线就是它的对称轴。
【详解】如图:
在常见的平面图形中,等边三角形有3条对称轴,圆有无数条对称轴。
5. 轴对称 平移
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴;在平面内,把一个图形整体沿某条直线方向平行移动一定距离的过程,称为平移;平移前后,物体的大小、形状和方向均不会改变,只是位置发生变化。
【详解】由图可知,图形A和图形B关于中间的直线对称,所以图形A通过轴对称可以得到图形B;图形B和图形C形状、大小和方向都一样,所以图形B通过平移能得到图形C。
仔细观察,图形A通过轴对称可以得到图形B,图形B通过平移能得到图形C。
6. ④ 左 2
【分析】在平面内,把一个图形整体沿某条直线方向平行移动一定距离的过程,称为平移。
根据题意可知,把④号小正方形平移到图中③号和⑤号小正方形之间就可以得到大写英文字母“T”。据此解答。
【详解】根据分析可知, 通过平移④号小正方形可得到大写英文字母“T”,如下图:
则将④号小正方形向左平移2格可以得到大写英文字母“T”。
7. ② ③ ①
【分析】轴对称图形定义为平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形。直线叫做对称轴,并且对称轴用点画线表示,据此判断图形有几条对称轴即可。
【详解】
①如图:,圆形有无数条对称轴;
②如图:,该图形有两条对称轴;
③如图:,该图形有四条对称轴。
图形中有2条对称轴的是②,有4条对称轴的是③,有无数条对称轴的是①。
8.非
【分析】沿一条直线对折后两部分可以完全重合的图形叫做轴对称图形。把图形补全,使它成为一个轴对称图形,需要在对称轴的另一侧找到对应的顶点,依次连接这些点;据此解答。
【详解】根据解析补成完整以后的汉字是,所以完整的汉字可能是非。
9.C
【分析】一个图形沿一条直线对折,直线两旁的图形完全重合,这样的图形叫做轴对称图形,折痕所在的直线就是对称轴。分析每个选项中图形的对称轴数量,选出符合要求的即可。
【详解】A.正方形有4条对称轴;
B.长方形有2条对称轴;
C.五角星有5条对称轴。
5>4>2
所以,五角星的对称轴数量最多。
故答案为:C
10.B
【分析】在平面内,把一个图形整体沿某条直线方向平行移动一定距离的过程,称为平移;平移前后,物体的大小、形状和方向均不会改变,只是位置发生变化。由题意得,平移原来的图形,要使它和其它图形能够重合,那么它们的大小、形状和方向均应该相同。
【详解】A.由图可知,选项中的小鸟与原来图形的方向不一样。不满足题意。
B.由图可知,选项中的小鸟与原来图形的大小、形状和方向均一样。满足题意。
C.由图可知,选项中的小鸟与原来图形的大小不一样。不满足题意。
故答案为:B
11.C
【分析】数平移的距离可以在找出图形中任意找出某个“关键点”,这个“关键点”平移之前的位置和平移之后的位置之间的距离,就是平移的距离。如下图,两个红点之间的距离是4格,也就是图形向右平移了4格。据此解题即可。
【详解】由分析可知:题中方格中的图形向右平移了4格。
故答案为:C
12.B
【分析】平移:在平面内,将一个图形上的所有点都按照某个方向作相同距离移动的图形运动。平移后图形的位置改变,形状、大小、方向不变。据此解答即可。
【详解】
A.,不能用其中一部分平移得到;
B.,可以用其中一部分平移得到;
C.,不能用其中一部分平移得到;
D.,不能用其中一部分平移得到。
甲骨文是汉字的源头和中华优秀传统文化的根脉。下列甲骨文中,能用其中一部分平移得到的是。
故答案为:B
13.C
【分析】根据题意,可以将左边阴影部分向右平移4格后和右边阴影部分组成一个长为4cm宽为2cm的长方形,根据长方形面积=长×宽,据此代入数字计算出面积选择即可。
【详解】4×2=8(cm2)
图中阴影部分的面积之和是8cm2。
故答案为:C
14.D
【分析】平移,是指在同一平面内,将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动,简称平移。平移不改变图形的形状和大小。
两组对边分别平行且相等的四边形是平行四边形,只有一组对边平行的四边形是梯形;
根据平移移动各三角形与梯形拼一拼,再根据平行四边形特点判断即可得出结论。
【详解】
A.图①向下平移两格,与梯形组成的图形是,不是平行四边形;
B.图②向下平移两格,再向左平移两格,与梯形组成的图形是,不是平行四边形;
C.图③向上平移两格,再向右平移两格,与梯形组成的图形是,不是平行四边形;
D.图④向上平移两格,再向左平移三格,与梯形组成的图形是,是平行四边形;
所以,通过平移可以和梯形拼成一个平行四边形的是④。
故答案为:D
15.B
【分析】把一个图形沿着某一条直线折叠,如果直线两旁的部分能够互相重合,那么称这个图形是轴对称图形,这条直线就是对称轴,据此解答即可。
【详解】
分析可知,如图所示的小花图案是从对折的纸上剪下来的。
故答案为:B。
16.B
【分析】把一个平面图形沿一条直线对折,折痕两边的图形能够完全重合,这样的图形叫做轴对称图形,折痕所在的直线是轴对称图形的对称轴。据此解答。
【详解】
A.沿图中直线对折,折痕两边的图形能够完全重合,是轴对称图形;
B.无论怎么对折,折痕两边的图形不能完全重合,不是轴对称图形;
C. 沿图中直线对折,折痕两边的图形能够完全重合,是轴对称图形;
故答案为:B
17.见详解
【分析】补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。由题意得,补全三角形的另一半后,三角形的两条斜着的边的长度相等,所以这是一个等腰三角形。满足题意。
【详解】
18.见详解
【分析】补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【详解】
19.(1)(2)见详解
【分析】(1)根据平移的特征,把小树的各顶点分别先向上平移5格,再向右平移7格,依次连接即可得到平移后的图形。
(2)根据题意,先把小鱼向上平移6格,再向左平移5格,就可以得到小鱼原来的位置。
【详解】(1)(2)如图:
20.(1)见详解
(2)见详解
(3)等腰;锐角
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的另一边画出右图的关键点的对称点,依次连结即可;
(2)根据平移的特征,把三角形的各个顶点分别先向上平移2格、再向左平移5格,再依次连结各顶点的对应点,即可得到图形②平移后的图形;
(3)有两条边相等的三角形是等腰三角形;三个角都是锐角的三角形是锐角三角形;据此解答。
【详解】(1)(2)如图:
(3)按边分,图形②是等腰三角形;按角分,图形②是锐角三角形。
21.551平方米
【分析】将这两条小路平移后可知,草坪的面积等于长(30-1)米,宽(20-1)米的长方形的面积,根据长方形的面积=长×宽,求出草坪的面积。
【详解】(30-1)×(20-1)
=29×19
=551(平方米)
答:草坪的面积是551平方米。
22.28米
【分析】把各不规则部分的横线段和竖线段进行平移,可得到所求周长恰好是长为12米,宽为2米的长方形的周长,用(长+宽)×2,即可求出小路长。
【详解】(12+2)×2
=14×2
=28(米)
答:小路长28米。
【点睛】此题主要考查学生对矩形两组对边对应相等的性质的掌握情况,做这类题时还需注意利用平移的思想。
23.(1)(3)见详解
(2)12
【分析】(1)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴虚线的下边画出上半图的关键对称点,依次连接即可。
(2)由图可知,这个图形的一周有12个小方格的边长,所以它的周长是12厘米。
(3)根据平移的特征,把这个轴对称图形的各顶点分别向左平移4格,依次连接即可得到平移后的图形。
【详解】(1)(3)如图
;
(2)这个轴对称图形的周长是12厘米。
24.(1)图见详解;等腰;
(2)(3)(4)见详解
【分析】(1)先从ABCD四个点中任选3个点画一个三角形(画法不唯一),等腰三角形的两腰相等,从三角形的一个顶点到它的对边作一条垂线,顶点和垂足之间的线段叫做三角形的高,这条对边叫做三角形的底,依此画图。
(2)物体平移的方法是点对点平移,然后将所有点依次连接起来,依此画出平移后的图形。
(3)根据三角形高的意义,在三角形中,从一个顶点向它的对边所在的直线画垂线,顶点到垂足之间的线段叫做三角形的高,再根据过直线外一点画已知条直线的垂线的方法,由此作图即可。
(4)补全轴对称图形的方法:找出图形的关键点,依据对称轴画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
【详解】(1)先从ABCD四个点中任选3个点画一个三角形。如图:
这是一个等腰三角形。
(2)然后画出三角形向下平移6格后的图形。如图:
(3)再在平移前的三角形中,以最长边为底,画出底边上的高。如图:
(4)画出轴对称图形的另一半。如图:
(三角形画法不唯一)
25.(1)(2)见详解
(3)54平方厘米
【分析】(1)补全轴对称图形的方法:找出图形的关键点,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,依此画出关键点的对称点,再依据图形的形状顺次连接各点,画出最终的轴对称图形。
(2)作平移后的图形的方法:找出构成图形的关键点,过关键点沿平移方向画出平行线,由平移的距离确定关键点平移后的对应点的位置,再依据图形的形状顺次连接各对应点,画出最终的图形。
(3)先数出整格数以及不完整的格数,把不完整格按半格计算,再加上整格数,估算出面积。
【详解】(1)(2)如图:
(3)50+8÷2
=50+4
=54(平方厘米)
这个轴对称图形的面积是54平方厘米。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
